AWK-TIS:An Improved AK-IS Based on Whale Optimization Algorithm and Truncated Importance Sampling for Reliability Analysis

Qiang Qin,Xiaolei Cao and Shengpeng Zhang

1Aerospace Science and Industry Corporation Defense Technology Research and Test Center,Beijing,100854,China

2Key Laboratory for Thermal Science and Power Engineering of Ministry of Education,Department of Engineering Mechanics,Tsinghua University,Beijing,100084,China

ABSTRACT In this work,an improved active kriging method based on the AK-IS and truncated importance sampling(TIS)method is proposed to efficiently evaluate structural reliability.The novel method called AWK-TIS is inspired by AK-IS and RBF-GA previously published in the literature.The innovation of the AWK-TIS is that TIS is adopted to lessen the sample pool size significantly,and the whale optimization algorithm(WOA)is employed to acquire the optimal Kriging model and the most probable point(MPP).To verify the performance of the AWK-TIS method for structural reliability,four numerical cases which are utilized as benchmarks in literature and one real engineering problem about a jet van manipulate mechanism are tested.The results indicate the accuracy and efficiency of the proposed method.

KEYWORDS Structural reliability;active kriging;whale optimization algorithm;AK-IS

Nomenclature

AK Active kriging

TIS Truncated importance sampling

WOA Whale optimization algorithm

MPP Most probable point

MCS Monte Carlo simulation

FORM First order reliability method

SORM Second order reliability method

LSF Limit state function

RBF Radial basis function

DOE Design of experiment

ξ Regression coefficient vector

z(x) Stationary Gaussian process

σz2Process variance

R(xi,xj) Correlation function

θ∗Optimal correlation parameter

PfFailure probability

δPfCoefficient of variation of the failure probability

λPositive penalty coefficient

ζSmall constant

χThreshold

x(t)ii-thsearch agent in thet-thiteration

The best agent in thet-thiteration

AiRandom value

BiRandom value

CiRandom value

NISNumber of importance sampling

βReliability index

1 Introduction

Structural reliability analysis is often carried out to quantitatively assess the probability of structures’safe or failure state under the impact of uncertain factors in the environmental,structural and load parameters.Various structural reliability analysis methods,which can be broadly categorized into three main types:simulation-based methods,analytical methods or approximation methods,and meta-modeling methods,have been proposed over the past three decades[1,2].

Concerning simulation-based methods,the crude Monte Carlo simulation(MCS)method is the basic form of this classification,which evaluates the failure probability by dividing the number of samples falling into the failure domain by all the samples generated from the limit state evaluations.Although MCS is the most convenient implementation approach,it is extremely time-consuming when dealing with small failure probability and complex numerical models(e.g.,fidelity finite element models(FEM)).Meanwhile,tremendous variation techniques of the MCS such as subset simulation[3,4],importance sampling [5,6] and directional sampling [7,8] have been developed to obtain more accurate results with fewer samplings.However,the main drawback of insufficient still exists in those methods.

As analytical methods,the traditional first-order and the second-order reliability methods(FORM and SORM)[9–12]respectively approximate the limit state function(LSF)around the most probable failure point(MPP)with first-order and incomplete second-order functions.The derivatives of the LSF with respect to the random variables have thus to be evaluated.Hence,these methods are not suitable for implicit limit state function and high nonlinearity cases.

Meta-modeling methods have been developed to balance the computational accuracy and efficiency during the structural reliability analysis,such as response surfaces[13–15],polynomial chaos expansion [16,17],artificial neural networks [18,19],support vector machine [20,21],radial basis function(RBF)[22,23]and Kriging metamodel[24,25].In recent years,Kriging metamodel methods have obtained remarkable attention in the state-of-the-art literature.From the design of experiment(DOE) aspect of view,the strategy for constructing a Kriging model can broadly be classified into two sorts,the one is “one-shot”and the other is adaptive sampling or sequential sampling methods[26].Literally,“one-shot”means producing enough design points before generating a Kriging model without supplementing new sample points in succeeding courses.Nevertheless,the adaptive sampling methods generate a relatively small number of design points at the initial step,and then add one or more samples in each course of iteration according to certain regulations [27].Furthermore,the exclusive feature of Kriging that it can predict the local uncertainty along with the prediction value promotes the development of the adaptive Kriging[24,28].

Two typical algorithms,the efficient global reliability analysis(EGRA)[28]and adaptive Kriging(AK) with MCS (AK-MCS) [29],are generously adopted and depict outstanding characters in diverse structural reliability problems.The amount of research has then further ameliorated the performance of active Kriging-based methods in recent years.These ameliorations resort to different and more efficient learning functions,sampling schemes and stopping criteria.Learning functions include the expected feasible function(EFF)[28],the learning functionU[29],the learning functionH[30],expected risk function (ERF) [31],least improvement function (LIF) [32],reliability-based expected improvement function(REIF)[33],Folded Normal based Expected Improvement Function(FNEIF) [34],K-means and weighted K-medoids algorithms-assisted learning process [35],and PDEM-oriented expected improvement function (PEIF) [36].With regard to stopping criteria,it is common to see that when the values of learning functions reach certain thresholds the learning process stopped.For sampling tactics,importance sampling,subset simulation,line sampling,etc.have been adopted to evaluate failure probability in active Kriging(AK)reliability analysis,and some AK-based sampling methods were presented,such as AK-IS[37],AK-SS[38],AK-DS[39],AKOIS[40],AK-ARBIS [41],AK-SESC [42] and AKSE [43].By combining these sampling methods with learning functions,the number of calls of limit state functions has reduced dramatically with acceptable accuracy of variation coefficient of failure probability.Despite the aforementioned learning functions,the correlation parameterθalso plays a vital role in constructing an accurate Kriging model.Thus,the pattern search algorithm is applied in DACE to calculate the optimum ofθ[44].However,as a local optimization algorithm,pattern search is sensitive to the initial value and may get trapped in local optimum.Then,various global optimization algorithms,such as genetic algorithm(GA)[33,45],DIRECT algorithm[46],particle swarm optimization(PSO)[47],and artificial bee colony(ABC)[48],are adopted to find the optimal value ofθby solving the maximum likelihood equation.Compared with GA,PSO,and the pattern search,the whale optimization algorithm(WOA)[49]proposed in the year of 2016 has its own advantages,such as simple principle,easy implementation,high convergence speed and calculation accuracy.

This paper aims to improve the efficiency and accuracy of the AK-IS for structural reliability analysis.In this paper,AWK-TIS is proposed,which is inspired by AK-IS [34] and RBF-GA [50],coupling with WOA and Truncated importance sampling (TIS) [51,52],and the WOA in AWK-TIS is adopted to seek the optimum of correlation parameterθand the MPP in different phases of each course of iterations.Moreover,inside of the optimalβ-sphere treated as the safe state,the samples are eliminated by TIS.Therefore,the prediction of Kriging model and the selection of the best next sample are only implemented through the candidate samples outside the optimalβ-sphere,which significantly reduces the computational time and saves computer memory in comparison with the original AK-IS.

The remainder of the manuscript is organized as follows.Section 2 briefly introduces the Kriging method,AK-IS method,TIS and WOA.In Section 3,the procedures and the main steps of the AWKTIS method are proposed.In Section 4,the applicability of the proposed technique is validated by four numerical cases and one real engineering problem of jet van manipulation mechanism.Finally,conclusions are summarized in Section 5.

2 Backgrounds

Before introducing the proposed AWK-TIS algorithm,some basic theories are briefly recalled,e.g.,the Kriging method,the main steps of the AK-IS algorithm and truncated importance sampling(TIS)method,and the WOA.

2.1 Basic Theory about Kriging Method

Kriging metamodel,which consists of a parametric linear regression model and a nonparametric stochastic process,is an interpolation technique based on statistical theory.It needs a DOEs to determine its stochastic parameters and then predictions of the response can be inferred on any unknown point.Give a set of initial DOEsX=[x1,x2,...,xm],withxi∊Rn(i=1,2,...,m) theith experiment,andG=[G(x1),G(x2),...,G(xm)]is the corresponding response toX.The approximate relationship between any experimentxand the responseG(x)can be denoted as[41,42]:

whereξT=[ξ1,...,ξp]is a regression coefficient vector,fT(x)=is the basic functions vector which makes a global simulation in design space.In the ordinary Kriging,F(ξ,x)is a scalar and always taken asF(ξ,x)=ξ;z(x)is a stationary Gaussian process with zero mean and covariance between two data pointsxiandxjis denoted as:

whereσz2is the process variance,andxi,xjare data points from the whole samplesX.Ris the correlation function aboutxiandxjwith a correlation parameter vectorθthat has to be estimated by pattern search method in DACE.A diversity of models can be adopted to define correlation functionsuch as Gaussian correlative model,experimental and linear model,etc.The widely employed Gaussian model is accepted in the paper and can be defined as:

wherenis the dimension of the sample,xki,andθkare thekth components of data samplexi,xjandθ,respectively.

Define correlation matrixR=[R(xi,xj)]m×m,Fis am×1 unit vector,thenξandσz2are given by:

whereR,andare functions ofθ.

Then at an unknown pointx,the Best Linear Unbiased Predictor(BLUP)of the response(x)is shown to be a Gaussian random variant(x)∼N((x),(x)),where

wherer(x)=[R(x,x1),R(x,x2),...,R(x,xm)],v(x)=FTR−1r(x)−1.(x)is usually taken as the estimated(x)at pointx.That means Kriging is an exact interpolation method.

The correlation parameterθcan be obtained through the maximum likelihood estimation(MLE)[47,48]:

where |R| is the determinant ofR.The optimal Kriging model can be obtained if the optimal correlation parameterθ∗is guaranteed.The Eq.(8)can be solved by pattern search method,genetic algorithm,PSO,etc.It should be noted that since the introduction of WOA,this algorithm has been used in many fields and showed its superiority over many other metaheuristic algorithms such as PSO,ABC,GA,etc.As a result,WOA is adopted to searchθ∗in this study.

2.2 AK-IS Algorithm

AK-IS mainly consists of two steps.The first step is the FORM approximation,which is utilized to find the MPP that is not accurate enough to evaluate the probability.The second step is to establish an AK model with a special learning function and stopping criteria to reduce the calls of original limit state function.In this step,IS method is adopted to calculate the failure probability and its coefficient of variation.

IS requires the definition of a joint PDFϕnthat is taken as a standard Gausssian one centered at the MPP found in the first step for the new sampling.The failure probability is estimated as[37]:

whereIF(u)is indicator function,IF(u))={0 ifG(u)>0 and 1 ifG(u)≤0}.

A number ofNISsamples denotedare generated according to importance sampling density functionϕn.The integral is then expressed by:

The variance of the failure probability estimator is given as:

The coefficient of variationδISof the failure probability estimator is then:

Besides,the learning functionUproposed in AK-MCS is still used in AK-IS:

whereμ(x)andσ(x)are Kriging mean and standard deviation,respectively.Moreover,the sample that has the minimum ofU(x)is called the best next sample and it is iteratively enriched the DOE to update the Kriging model.The learning process stops if the minimum of the learning functionUis larger than its threshold.Besides,the active procedure continues andNISnew samples are enlarged until the coefficient of variationδISis smaller than a limit value which is set to 0.05 in AK-IS.

2.3 Truncated Importance Sampling

Truncated importance sampling(TIS)method is developed by introducing a hypersphere with the radial,which is indicated byβshown in Fig.1,equals to the minimum distance from the origin to the limit state surface inu-space[51,52].

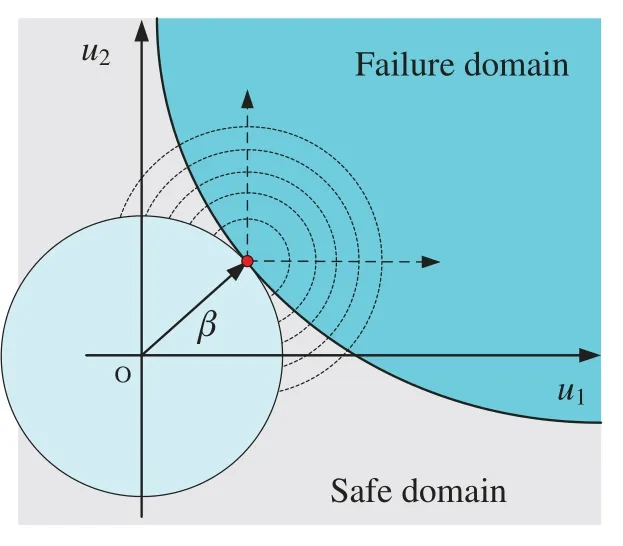
Figure 1:Sketch of TIS

The red point in Fig.1 indicates the MPP.

The indicator function of the outer of theβ-sphere is defined as follows:

where the inner of theβ-sphere contains part of the safe domain or even all of the district,while other domains including all the failure domain and part of the safe domain are out of theβ-sphere.It can be seen that the indicator functionIFof the samples located in theβ-sphere is=0,and there is unnecessary to call the true model to evaluate whether safe or not.The integral is then estimated by:

The variance of the failure probability estimator is estimated as:

The coefficient of variation(C.O.V)δTISof the failure probability estimator is then:

2.4 Whale Optimization Algorithm

The Whale Optimization Algorithm (WOA) is a novel nature-inspired population-based metaheuristic algorithm,presented by Seyedali Mirjalili and Andrew Lewis from Griffith University in 2016 [49].It was abstracted from the special hunting behavior of humpback whales.This foraging behavior is named bubble-net feeding method.

Two approaches namely,shrinking encircling mechanism and spiral updating position,are designed to mathematically model the exploitation phase of the WOA.The first approach is formulated as follows:

wheretindicates the current iteration,AiandCiare coefficients.x(t)iandrepresenti-thsearch agent and the best agent in thet-thiteration,respectively.

whereqis linearly reduced from 2 to 0 over the course of iterations,ri1,ri2are random numbers in[0,1].Aiis a random value in the interval [−2q,2q].When the random value ofAiis in [−1,1],the next position of a search agent can be in any position of the agent and the position of the current best agent.The parameterCiis a random value in [0,2].This component provides random weights for prey in order to stochastically emphasize(Ci>1)or deemphasize(Ci<1)the effect of prey in defining the distance between the search agent and the current best agent.Besides,the second approach,the process of spiral updating position,is expressed as follows:

wherebis a constant for defining the‘9’-shaped path of distinctive bubbles created by the humpback whales,lis a random number in[−1,1].

The humpback whales hunt the prey by using the shrinking circle mechanism and spiral updating method simultaneously,and the two approaches have the same possibility to be chosen,so the model of the exploitation phase is as follows:

whereri3are random numbers in[0,1]to switch the different mathematical model of exploitation.

However,the process of search for prey is defined as the exploration phase,and the model of this phase is described as follows:

wherex(t)jis thej-thrandom search agent which is different from thex(t)i,andAiis also defined by Eq.(19),but it is absolute value,|Ai|,is greater than 1 to emphasize exploration and let the WOA to search the whole search space.

3 AWK-TIS Algorithm

In this section,the main steps of the proposed method are introduced.Firstly,the WOA-Kriging model is constructed based on the basic Kriging model.Secondly,the AWK-TIS method is developed.

3.1 WOA-Kriging Model

In the proposed WOA-Kriging model,the optimal value of correlation parameterθ∗is calculated by integrating WOA into the basic Kriging model.The pattern search method is adopted to seekθ∗in DACE.However,the pattern search method is a local optimization algorithm that needs an initial solution to search the optimal and it is easy to get trapped in the local optimum.Alternatively,while seekingθ∗,as an efficient global optimization algorithm not depend on the initial solution.WOA is embedded in the DACE toolbox to solve Eq.(8),instead of pattern search algorithm.Then,in our implementations the fitness function for the MLE according to the correlation parameterθis to minimize the function below[45]:

Given the fitness function above,the finding process ofθ∗becomes a typical minimization problem.Thus,the population(whale positions)is firstly initialized in an-dimensional search space,and the population size is set to 25 in this study.Each position corresponds to a correlation parameter vector.Next,a set of mathematical rules in WOA such as encircling prey,spiral bubble-net feeding and search for prey are repeatedly conducted at each iteration.Then,the fitness values of every population are obtained,the fittest solution is ascertained.Finally,the global optimal correlation parameter is acquired until the satisfaction of the stopping criteria that is the maximum number of iterations equals to 100.The main WOA parameters are unchanged during the optimization procedure.Consequently,the WOA-Kriging model is constructed by the optimal correlation parameterθ∗.

3.2 The AWK-TIS Algorithm

In this subsection,the AWK-TIS algorithm is introduced in detail.In AWK-TIS,the real limit state function is substituted by a WOA-Kriging model; the failure probability and its coefficient of variation are computed by TIS method in an active learning way.AWK-TIS mainly consists of three components.Firstly,a WOA-Kriging model is constructed according to the optimal parameterθ∗searched by WOA and the DOE generated through Latin Hypercube Sampling method in the entire design space.Secondly,MPP is evaluated by WOA and the evaluation process is treated as solving a constrained optimization.Thirdly,the active learning method and TIS are adopted together to conduct the selection of the best next sample and the evaluation of the probability.At this stage,the WOAKriging model is updated according to the enriched DOE.The general sketch of the AWK-TIS is shown in Fig.2,and the detailed procedure is proposed as follows:

Step 1:Generation of the initial DOE.Latin Hypercube Sampling(LHS)method is employed to generate the initial samples in the whole design space.Then,the structural response or the real limit state function of every initial sample is evaluated.Thus,the initial DOE is composed of the initial samples and their corresponding responses.The number of the initial samples has an effect on the accuracy of the WOA-Kriging model;however,there are no certain rules to certificate this number.

Step 2:Construction of the WOA-Kriging model.Construct the WOA-Kriging based on initial DOE by embedding WOA to DACE toolbox to find the optimal parameterθ∗.Calculatingθ∗will spend a little more computing time,but it is worth since the time consumed for finding accurate parameters could be ignored compared with that for time-consuming simulations.The initial value ofθis unnecessary in this metamodel construction,and the correlation function is chosen to be the Gaussian function.

Step 3:Evaluation of the MPP.The WOA is utilized to calculate the MPP.The notion of reliability indexβ,is the minimum distance from the origin to the limit state surface in the standard normal space.The reliability index can be therefore calculated as the following constrained optimization problem[9,47,48]:

wherexdenotes the vector of random variants,which isx=(x1,x2,...,xn);denotes the standard normal variants;μxiandσxirepresent the mean and standard deviation of the random variantxi,respectively.(x)is the limit state function constructed by WOA-Kriging model.

Figure 2:General sketch of the AWK-TIS algorithm

The problem in Eq.(25)is a constrained nonlinear optimization problem.The aim of constraint optimization is to search for feasible solutions with better objective values.However,constrained optimization problems are difficult to solve than unconstrained optimization problems due to the presence of constraints and their interrelationship between the objective functions.As a result,the main assignment while solving the constrained optimization problem is to deal with the constraints.

Step 3.1:Construction of unconstrained function

To avoid the violation of constraints,unfeasible solutions should be adapted to feasible solutions.In the meta-heuristic community,the most common technique is to take advantage of penalty functions to handle these constraints.Thus,a penalty function is employed to convert the constrained optimization problem in Eq.(25)to the unconstrained one in Eq.(26)[21]:

where,λis the positive penalty coefficient,and its initial value is set to 103in this paper.

Step 3.2:Calculation of reliability index by WOA

The WOA is adopted to solve the unconstrained function.The inner loop is to find the optimal solution of the Eq.(26) by WOA,while the outer loop is to make sure that the reliability indexβis accurate enough.Thus,two stop criteria should be satisfied simultaneously as follows.First,the relative error between the reliability indices in two subsequent outer loop iterations is acceptable[47]:

wherekandk+1 indicate thek-th andk+1-th iteration in the outer loop,respectively,and relative errorζis a small constant(e.g.,0.01).

Second,it is required that the value of the WOA-Kriging model at the“potential”MPP should be relatively small which means that the“potential”MPP is rather close to the LSF[48]:

whereχis the threshold which is also a small constant(e.g.,0.0001).

If the two criteria above are met simultaneously,the MPP is acquired;otherwise,letλ=10λand go back to Step 3.1.It is noted that in this step the parameters in WOA are remain the same as its original version.

Step 4:Generation of NIS samples.NISsamples are generated according to importance sampling density function centered on the MPP found by Step 3.The response of those samples will be evaluated by WOA-Kriging if the active learning procedure requires it.

Step 5:Conduction of the active learning procedure.Add{xu,G(xu)}into the DOE set to rebuild the WOA-Kriging model,and evaluate the learning functionUamongNISsamples.The learning process continues until the stop criterion,i.e.,min(U(xi))>2 is satisfied,which means that the probability of making wrong sign estimation should not exceed 2.3%.

Step 6:Evaluation of the failure probability and the coefficient of variation δTIS.After the WOAKriging metamodel is constructed by the active learning method,the next step is to adopt TIS to analyze the reliability.The failure probability and the coefficient of variation are estimatedδTISby Eqs.(15) and (17),respectively,and make sure that theδTISsatisfies the predefined threshold.IfδTISdoes not satisfy the threshold,a set of newNISsamples are generated to enrich the originalNISsamples.In this paper,the threshold of theδTISis taken as 0.05.

Step 7:Output the unbiased estimation of the failure probability.IfδTISsatisfies the threshold,i.e.,δTIS≤0.05 then AWK-TIS terminates,and the failure probability is acquired.

4 Validation Cases

In this section,the efficiency of AWK-TIS is illustrated by four numerical cases and one engineering case.Each of the cases in this study has only a single failure region,which means only one MPP in each case.All the case results are averaged over 10 different runs.The accuracy and efficiency of different algorithms is compared according to the number of calls to the LSF (Ncall),δPf(the coefficient of variation of failure probability)andεPf(the relative percentage error of failure probability in comparison with the reference value).

4.1 Case 1:2D Application

A 2D numerical case,which has two independent random variables with standard normal distribution,is chosen to illustrate the process of the proposed method.The limit state function reads

In the proposed method,an initial Kriging model is constructed based on 12 samples within the domain of[±6]inuspace.The results of different methods are summarized in Table 1.The proposed method AWK-TIS is compared with AK-IS,MetaAK-IS2,AK-SS.The reference value evaluated by MCS with 5×107samples is taken from[37],and the value is 2.85×10−5.In order to test the robustness of AWK-TIS,10 different runs are performed withNIS=1×105initial samples centered on the MPP confirmed by WOA.According toNcall,i.e.,the number of calls to the LSF,the proposed AWK-TIS outperforms the majority of active learning Kriging-based methods except for AK-SS;however,theδPf,i.e.,the coefficient of variation of failure probability of AK-SS is higher than that of AWK-TIS.

Table 1: Results of the 2D application:Case 1

Furtherly,the approximation process of the limit state function is schematically illustrated in Fig.3,including LSF(green line),Kriging model(red dotted line),initial samples(black fork dots),added samples(pink circle)and MPP(blue hexagon).Moreover,the MPP searched by WOA is located almost in the same position after 5 iterations while the enriched DOE are updated sequentially byUlearning function.The convergence process of failure probabilityPfand the C.O.V ofPffor AWK-TIS are presented in Fig.4.

It can be seen from Figs.3 and 4 that these newly computed samples are located in the vicinity of the limit state function and are used to improve the accuracy of Kriging metamodel.Moreover,AWK-TIS requires much less performance function computations than AK-IS.Indeed,AWK-TIS needs 9 computations of real limit state function after the construction of Kriging model by initial DOE.

As described in Section 2.4,the WOA is adopted to acquire the correlation parameterθ.The number of search agents is 25,the number of iterations is set to 100,and other parameters in WOA are remaining as the original form.Fig.5 depicts the convergence of the Kriging correlation parameterθshown in Eq.(8)when the update process of the WOA-Kriging model is stopped.Moreover,Fig.5 shows that the maximum likelihood estimation ofθconvergence to the minimum value of 6.49×10−6at the 16thiteration,and the optimumθis found at this point.Compared with PSO and GA,the WOA shows its high convergence speed and calculation accuracy.

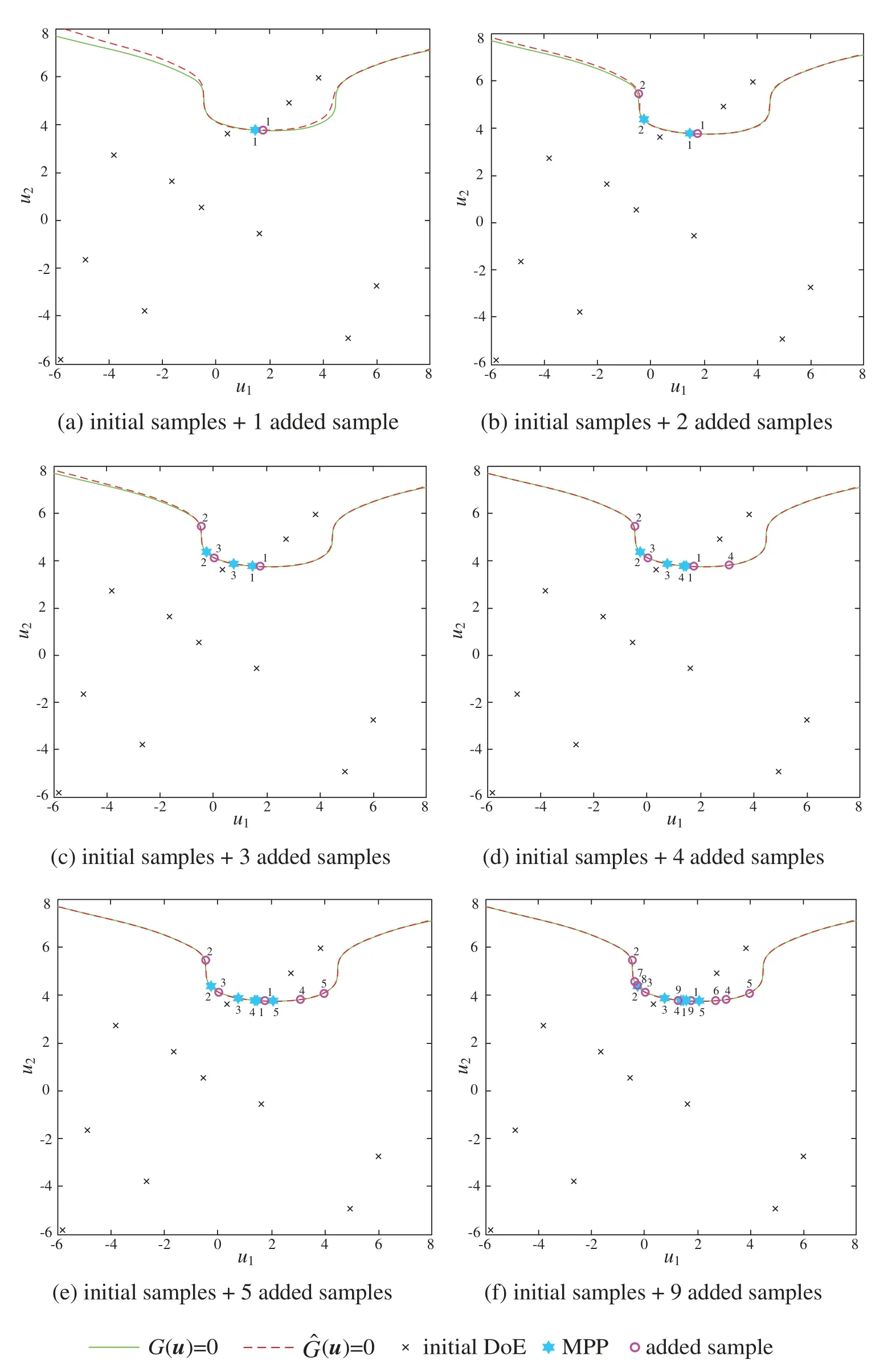
Figure 3:The approximation process of the LSF for case 1

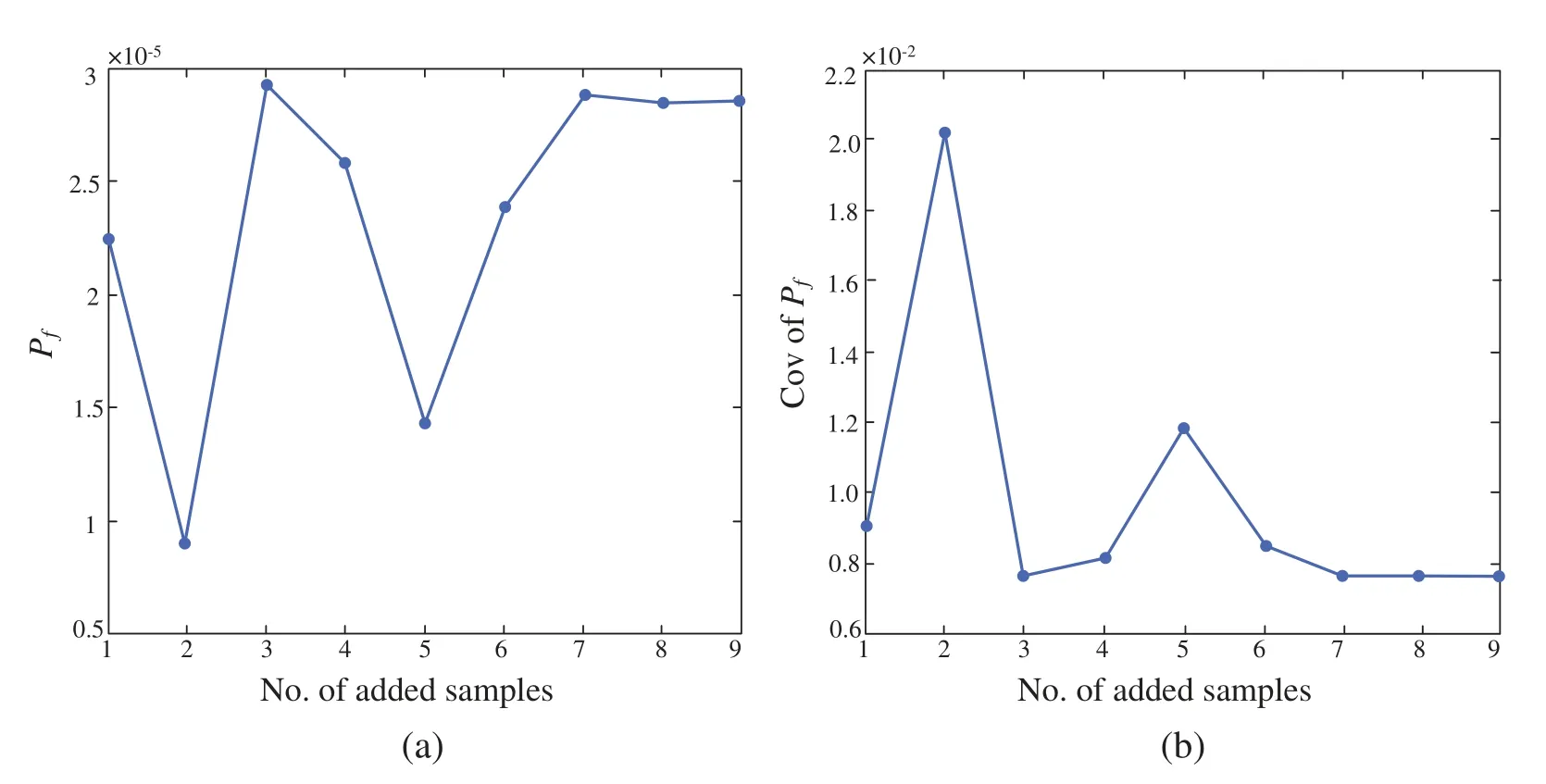
Figure 4:Convergence process of Pf and C.O.V of Pf for case 1

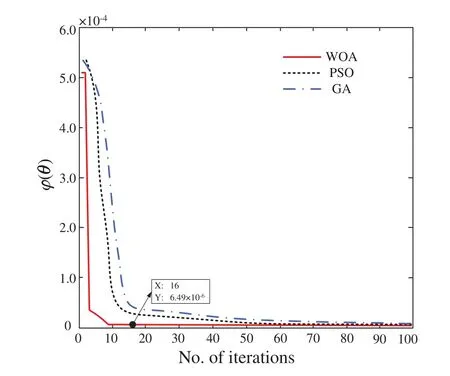
Figure 5:The process to find θ∗using WOA for case 1

4.2 Case 2:A Cantilever Beam Example

This case has been widely used in literature [38].The cantilever beam,which has a rectangular cross-section,is subjected to a distributed uniform load.The limit state function which is defined by the maximum vertical displacement of the beam is given as

wherex1andx2are assumed to be independent random variables following normal distribution.The statistical properties of the above two variables are shown in Table 2.The results obtained by the proposed AWK-TIS,MSC,AK-MCS,and AK-SS are listed in Table 3.

Table 2: Statistical properties of the variables for case 2

Table 3: Results of case 2

From Table 3,it can be seen that theNcallof the proposed AWK-TIS is the same as that of AK-SS,but it is less than the number of samples applied in AK-MCS.Besides,the one can see that all thePfcalculated by the different methods have high accuracy comparing with the MCS solution.However,the coefficient of variation of failure probability of AWK-TIS is the smallest in the four methods.

Similarly to Figs.3 and 4,Fig.6 shows the final approximation of AWK-TIS and Fig.7 shows the convergence process of failure probability and the C.O.V of failure probability.As shown in Fig.6,the added samples are almost in the vicinity of the real LSF,and the LSF constructed by Kriging can be accurately approximated in the domain of the sampling region.On the contrary,the Kriging model shows inexact outside the sampling region.Nevertheless,it should be indicated that the region outside the sampling area has little influence on the failure probability calculation due to the MPP is far away from this area.From Fig.7,the proposed method has converged to the final results at about 12 added samples,which indicates the efficiency and accuracy of the AWK-TIS.

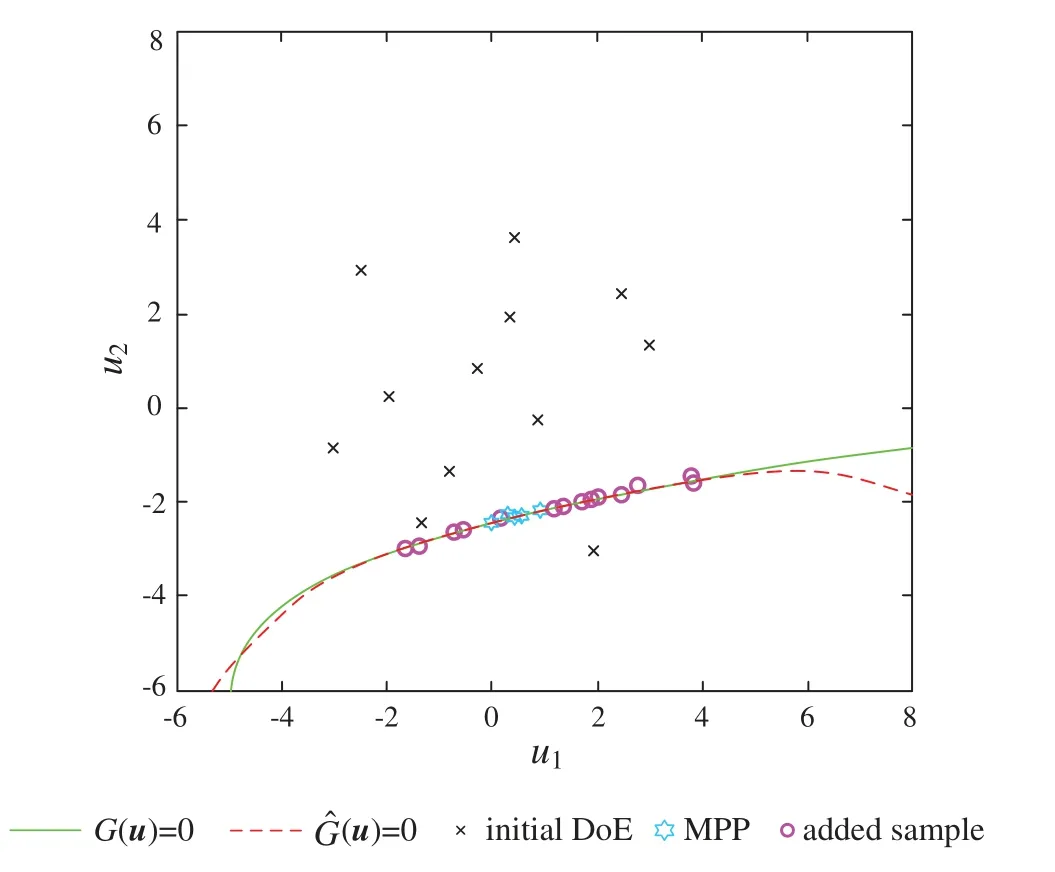
Figure 6:The approximation of the LSF for case 2

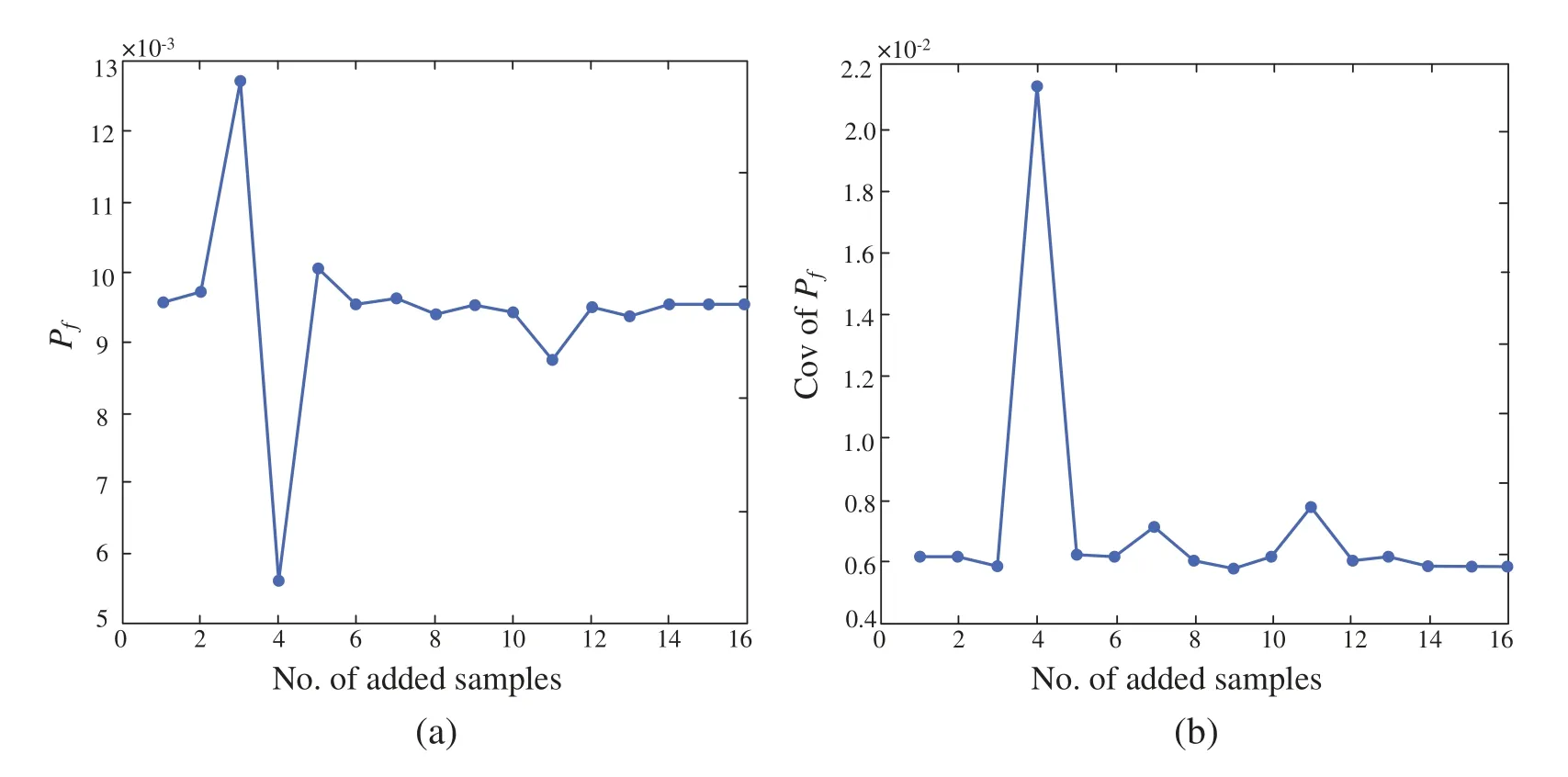
Figure 7:Convergence process of Pf and C.O.V of Pf for case 2

4.3 Case 3:A Non-Linear Oscillator

A non-linear undamped single degree of freedom system depicted in Fig.8 is analyzed in this case.The limit state function is given as[54]

whereω0=Six random input variables includingC1,C2,M,R,T1,andF1are listed in Table 4.The initial number of DOE is set as 20.The AWK-TIS is compared with several other existing methods (MCS,AK-MCS,PAK-Bn[54]) and their results are listed in Table 5.Same as the two cases above,the reference values to compare the reliability analysis results are thePf,,C.O.V ofPf,δPf,εPf,estimated by MCS.

Figure 8:A non-linear oscillator

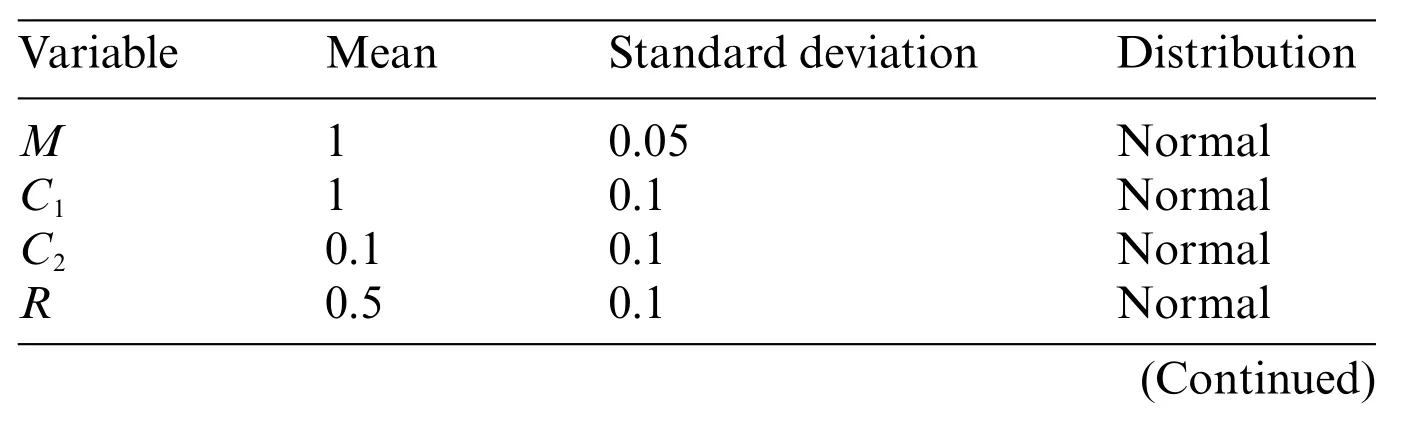
Table 4: Statistical properties of the variables for case 3

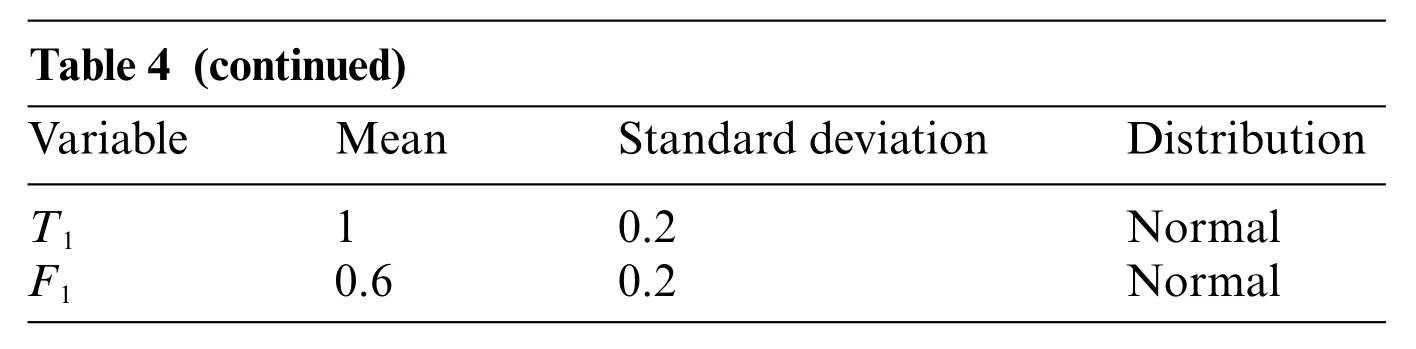
Table 4 (continued)VariableMeanStandard deviationDistribution T110.2Normal F10.60.2Normal

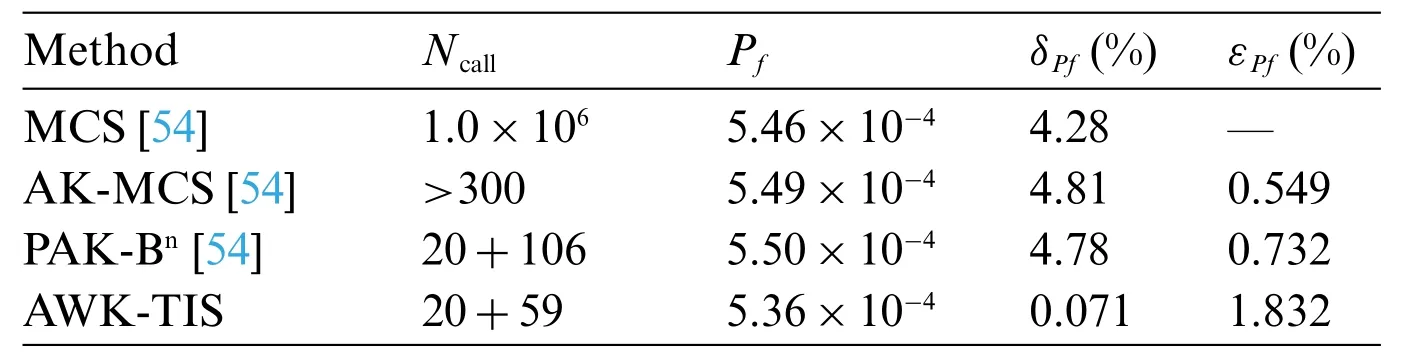
Table 5: Results of case 3

It can be seen from Table 5 that although the relative error of failure probability obtained by the proposed method is slightly larger than that of AK-MCS and PAK-Bn,theNcallof AWK-TIS is significantly reduced contrasted with that of the two methods above.Additionally,the C.O.V of failure probability is rather small compared with the other three methods.Hence,it indicates that AWK-TIS could solve the problem of small failure probability with a moderate number of random variables.

Equally,Fig.9 presents the convergence process of failure probability and C.O.V of failure probability of this case.From Fig.9,one can see that the failure probability has converged with almost 50 added samples,which means that the proposed AWK-TIS is suitable for the calculation of the small failure probability.

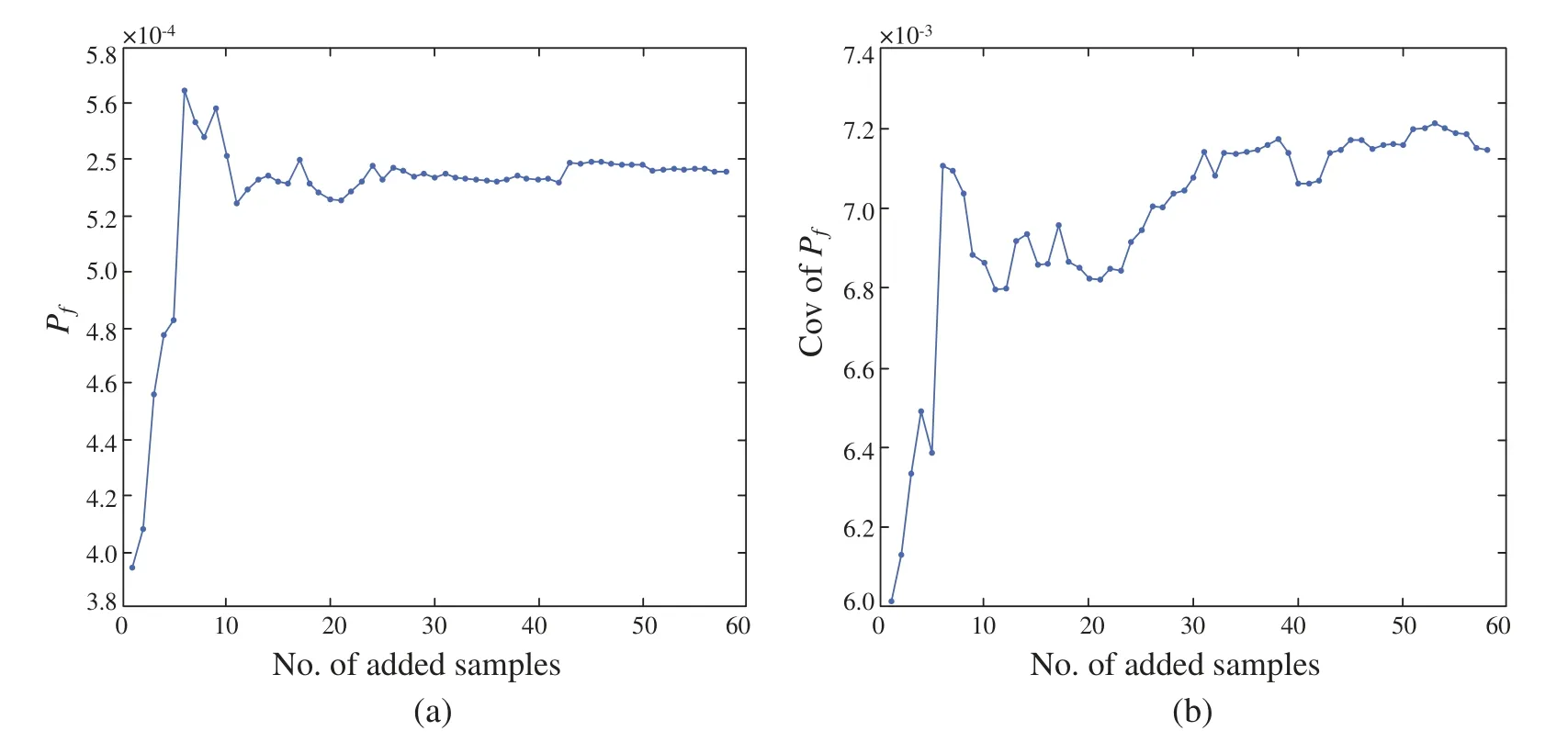
Figure 9:Convergence process of Pf and C.O.V of Pf for case 3

4.4 Case 4:A Roof Truss Structure

A roof truss structure,which is selected to verify the proposed method,is shown in Fig.10.The roof truss undertaking the uniformly distributed loadqthat can be converted to the nodal loadP=ql/4.The response of the roof truss is the perpendicular deflection △Cof nodeCis denoted as[55]:

whereAC,AS,EC,ESrespectively are sectional area,elastic modulus concrete and steel bars,lis the length of the structure.The mean and variation coefficient of the six independent normal distribution random variables are reported in Table 6.The threshold of △Cshould not be larger than 0.03 m,and the LSF of this case is thus defined as

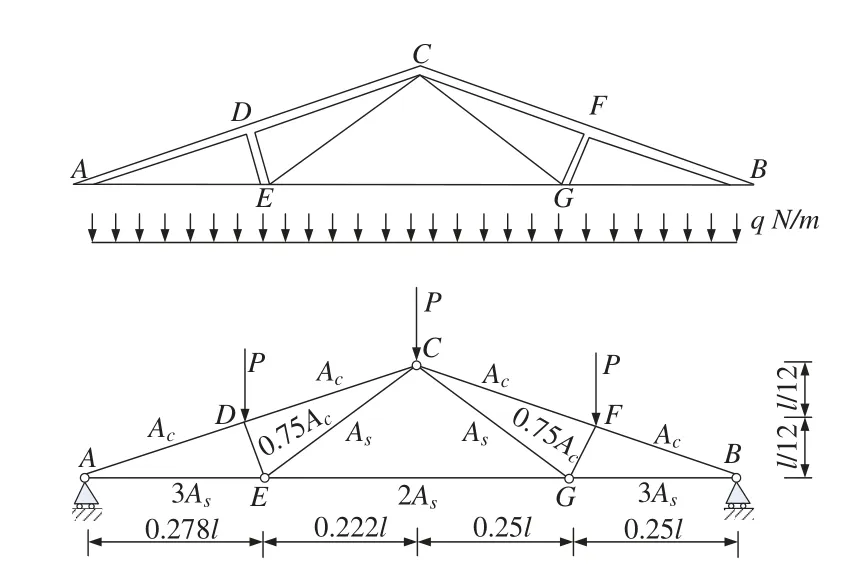
Figure 10:The schematic diagram of a roof truss

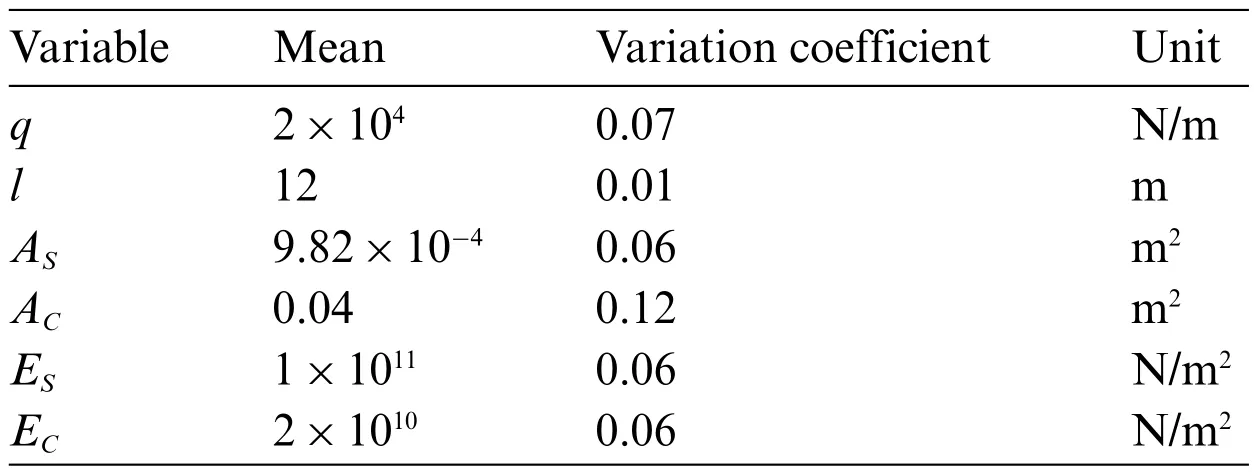
Table 6: Statistical properties of the variables for case 3

The AWK-TIS is compared with other existing methods (MCS,AK-MCS,KAIS,RBF) and the results are summarized in Table 7.The results by MCS calculations with 1.06×106samples are regarded as reference values in this case.

Table 7: Results of case 4

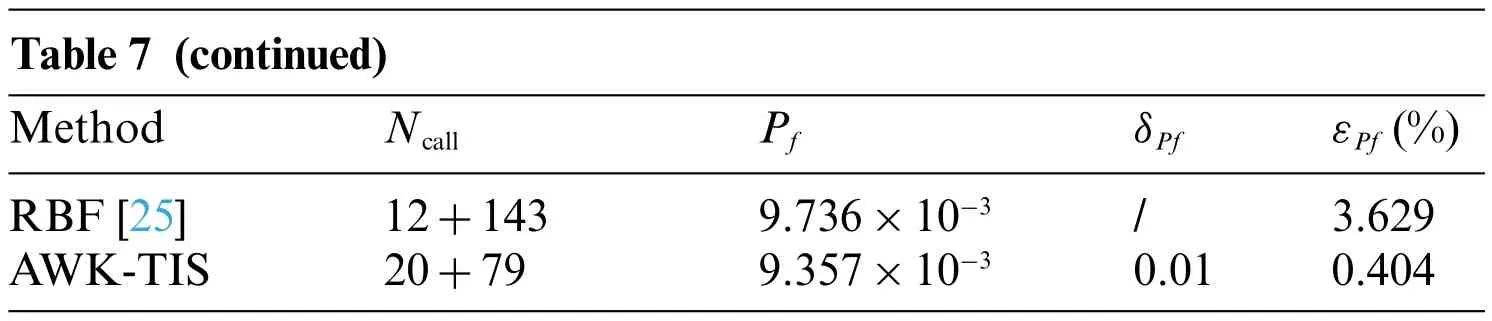
Table 7 (continued)MethodNcallPfδPfεPf(%)RBF[25]12+1439.736×10−3/3.629 AWK-TIS20+799.357×10−30.010.404

It can be seen from Table 7 that AWK-TIS needs only 99Ncallto acquire a satisfactory result while the other three approaches demand more than 150Ncall.The smallNcallhas highlighted the numerical efficiency of the proposed approach in estimating the roof truss structure.Furthermore,the AWK-TIS has the second relative error of 0.404%comparing with the reference value ofPfevaluated by MCS,followed by AK-MCS and RBF.

By investigating the convergence process ofPfand C.O.V ofPfpresented in Fig.11,we can see that both of the curves converged at about 25 added samples,which means that the proposed AWK-TIS is suitable for dealing with small failure probabilities and relatively large number of random variables.Additionally,the convergence threshold can be advisably loosed to further improve computational efficiency.

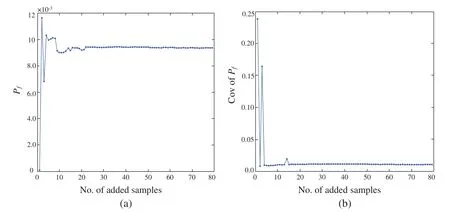
Figure 11:Convergence process of Pf and C.O.V of Pf for case 4

4.5 Case 5:A Jet Vane Manipulation Mechanism

Vertical launch missile is widely used on land air defense and sea air defense.The performance of a jet vane system is extremely vital to the flying control of vertical launch missile.As a significant component of the jet van system,the manipulation mechanism drives the rudder rotating in the engine gas flow that generates pitch moment to control the orientation of the missile,which is shown in Fig.12a.The manipulate mechanism convers the linear motion of the servo motor to the rotation of the jet van,and the schematic of this mechanism is shown in Fig.12b.

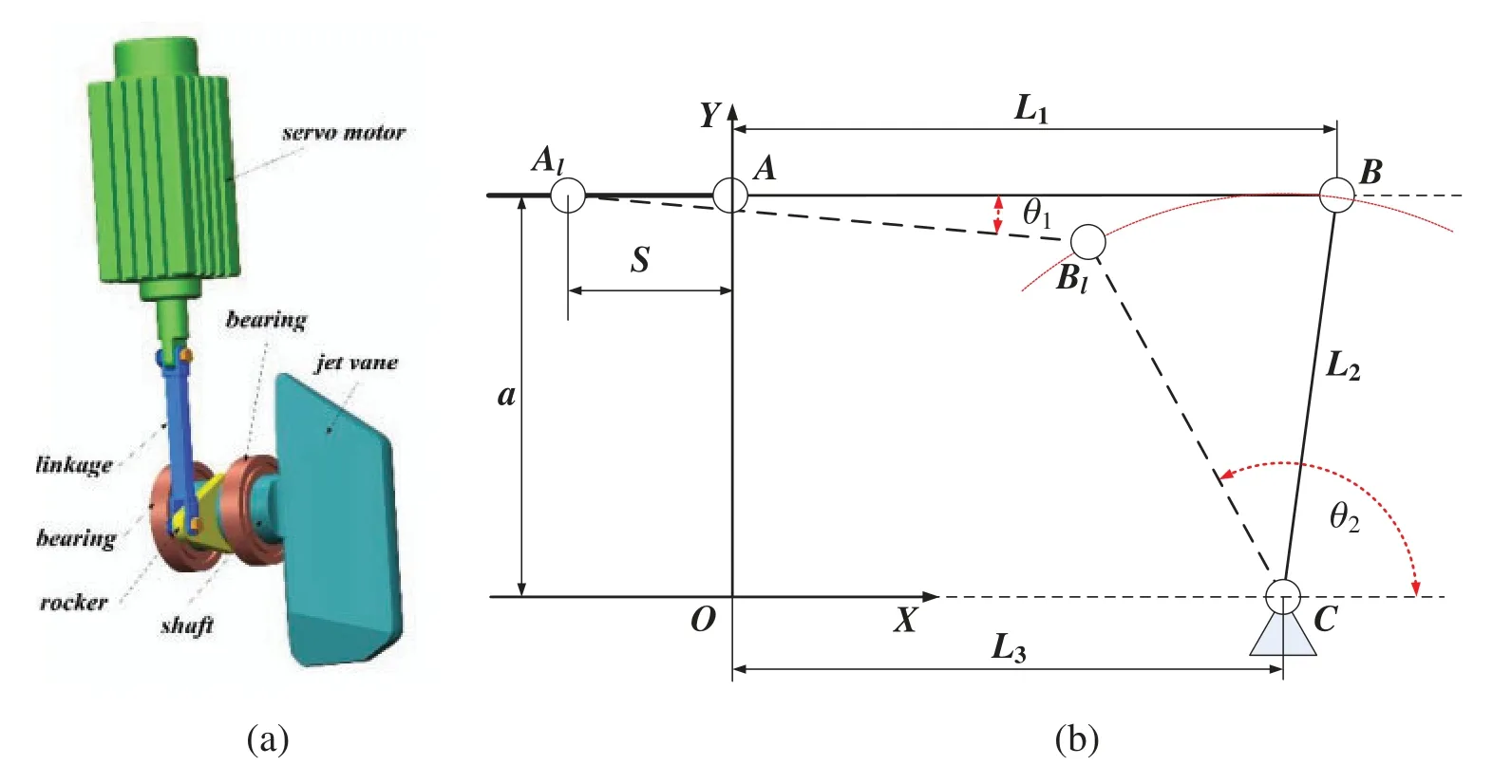
Figure 12:A jet van manipulation mechanism

In Fig.12b,AandBrepresent the positions of the two ends of the linkage respectively,andCis the center of the shaft.L1andL2are the length of linkage and rocker respectively.L3is the distance betweenAandCalong theX-axial.ais the distance betweenAandC.Sis the maximum displacement ofAalong the negative direction ofX-axial,andAl,Blare the left limit position of the linkage.θ2is the angle between theBCand theX-axial,and it is the function ofL1,L2,L3,aandS,which is shown in Eq.(34)

whereθ1is the angle between the linkage and the X-axial.

In this case,the linkage lengthL1,the length of the rockerL2,the distance betweenAandCalong the X-axialL3,and the maximum displacement of linear servo systemSare taken as random variables.Table 8 lists the details of random variables.To assure the normal operation of the manipulation mechanism,the maximum angle of the rudder shaft should not exceed a given threshold.Therefore,the limit state function is defined as

whereθmis the threshold of the maximum angle of the rudder shaft which is taken as 118.2°,θ2(X)is the maximum angle of the rudder shaft which is calculated by solving Eq.(34),theXrepresents all the random variables.

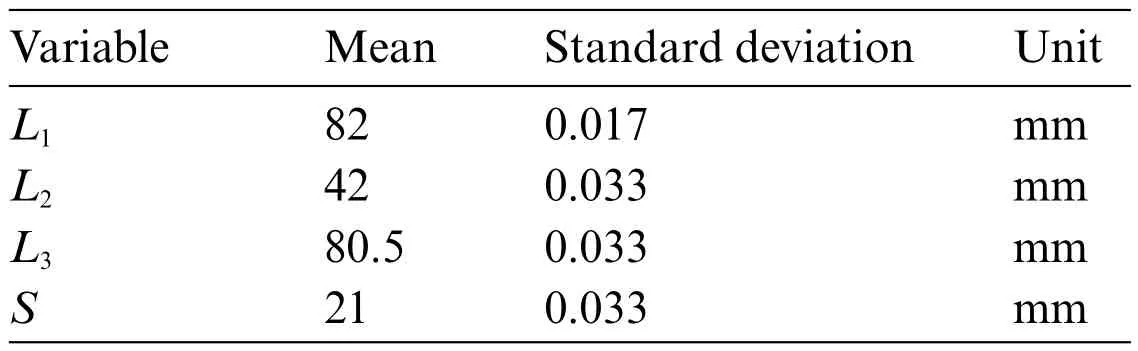
Table 8: Statistical properties of the variables for case 5

The results of the different methods are shown in Table 9,in which results estimated by the AKMCS and AK-IS methods are also provided for the sake of comparison.Besides,the calculation times or CPU-time of different AK-based algorithm are also exhibited in this table.The sample pool of the MCS,AK-MCS and AK-IS are 5×107,5×106and 4×106,respectively.

Table 9: Results of the case 5

Table 9 shows that the predictive accuracy of the AWK-TIS notably outperforms the other two AK methods considering the relative error of failure probability.Besides,theNcallis less than that of AK-MCS and AK-IS,which indicates that the proposed AWK-TIS can solve real engineering problem efficiently.From the CPU-time results,it is concluded that although the process of optimizing Kriging model by WOA algorithm additionally increases the computational time,the utilization of the TIS method reduces the calculation time.

The convergence of failure probability and coefficient of variation of failure probability is presented in Fig.13.From Fig.13,thePfand C.O.V ofPfhave converged to the final results at about the 10 added samples.Thus,the computational performance of the AWK-TIS when dealing with this case can be improved with a loose stopping criterion.

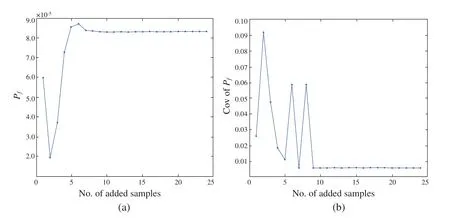
Figure 13:Convergence process of Pf and C.O.V of Pf for case 5

5 Conclusions

The AWK-TIS method is proposed as a novel reliability method to deal with structural reliability problems,in which the WOA is performed to seek the optimum correlation parameter of Kriging model and the MPP,and then the added samples generated byUlearning function are enriched to DOE to refine the Kriging model.The MPP is calculated by WOA through solving the constrained nonlinear optimization problem until certain two thresholds are satisfied simultaneously.Afterward,the TIS method is applied to calculate the failure probability and coefficient of variation of the failure probability.In AWK-TIS,the sample pool is much smaller than that of AK-IS,which significantly expedites the learning efficiency.Five test cases including four numerical cases and one engineering case are adopted to verify the performance of the AWK-TIS method.Results prove that the proposed method can achieve high computational accuracy and efficiency.

AWK-TIS method has two main drawbacks:(1)AWK-TIS,like AK-IS,is dependent on the MPP to ensure the next best point; however,the solitary sampling center has confined its employment in dealing with multi-MPP problems,(2)the process of acquiring the MPP is transformed to solve the constrained nonlinear optimization problem,which may affect the efficiency of the proposed method,(3) due to the restriction of IS-based algorithm,the proposed algorithm does have some defects in dealing with high-dimensional problems.Future works will focus on three aspects: (1) adopt other efficient sampling methods in lieu of TIS to solve multi-MPP problems,(2)improve the efficiency of WOA by hybridising other optimizers or employing other more effective optimization algorithms to solve the constrained optimization problem to obtain the MPP,(3)alternative modeling and analysis methods need to be incorporated for effective validation of AWK-TIS to high-dimensional problems.

Funding Statement: This work is supported by the Technical Basic Scientific Research Projects of State Administration of Science,Technology and Industry for National Defence,PRC (Grant No.JSZL2019204C001).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.