基于时间序列疏系数模型的太阳辐射年际变化趋势预测
2023-02-25贾兴斌宫响
贾兴斌,宫响
(青岛科技大学 数理学院,山东 青岛 266061)
太阳能作为清洁的可再生能源,其有效开发利用有助于人类生存环境的改善与经济社会的发展。但由于地表太阳辐射易受气候变化、大气污染、日照时长与云量等因素的影响[1],可利用的太阳能表现出一定的不稳定性和不连续性。研究发现,从1957年地面太阳辐射观测网建立以来,20世纪90年代前后,全球大部分区域地表太阳辐射经历了减少到增加的变化,即先“变暗”后“变亮”[2-3]。不同区域由于地理环境和影响太阳辐射的主要因素不同,太阳辐射还存在“振荡”现象[4-5]。因此,预测地表太阳辐射的长期变化趋势,不仅对研究人类活动在全球气候变化中的作用有重要意义,也可以为新能源利用如光伏电站的建设提供参考。
国内外学者对于地表太阳辐射的预测,主要采用基于经验参数的统计模型以及基于数理方程的大气数值模式。区别于上述方法,时间序列分析仅以时间为唯一自变量,根据已有的历史数据对未来进行预测。其中,自回归整合移动平均(auto regression integrated moving average,ARIMA)模型是一种经典的时间序列分析方法,具有较高的预测精度。这一模型在经济学、医疗卫生、气象等领域已得到广泛应用[6-9],近年来在地表太阳辐射的预测研究中也日益受到重视。如张素宁等[10]发现在地表太阳辐射的逐时预测中,ARIMA模型优于经验模型。Sun等[11]利用ARMA-GARCH模型,有效拟合出北京和乌鲁木齐两站位地表太阳辐射的月变化。Shadab等[12]基于ARIMA模型,利用印度马德里34年的遥感地表太阳辐射数据较好地预测了其未来24个月的变化。但目前仍缺乏ARIMA模型在地表太阳辐射年际变化的应用研究。
本文利用济南站1961—2016年地表太阳辐射的年数据,初步识别ARIMA模型,通过对模型参数及残差序列进行检验确定最优ARIMA疏系数模型,并分析预测未来10年的太阳辐射年际变化。
1 数据及方法
1.1 数据来源及处理
山东省是典型的重工业经济省份,其较为成熟的产业集群大都集中于能源、化工等传统领域,而代表未来经济发展方向的新能源、新材料、节能环保等新兴产业却没有形成足够的规模。同时山东人口众多,资源能源消耗强度大,随着城镇化进程的加快,城市污染日益凸显,进而导致地面太阳辐射变化[13]。
山东省目前有济南、莒县和福山三个国家级辐射观测站,其中济南站的观测序列最长,且济南市属于内陆城市,环境污染问题较为突出。因此,本文选取济南市1961—2016年的地表太阳年总辐射数据作为研究对象。该数据集下载于国家气象科学数据中心[14],其中1978年和1979年的数据缺失,采用月辐射数据补全,对其中缺失月份(1978年7月、1978年8月、1979年3月)进一步采用日辐射数据补全。而日辐射数据中也存在部分数据缺失,其中1978年7月有12天、8月份有3天,而1979年3月仅有前15天的数据。考虑到1978年8月的日数据缺失较少,故采用当月数据均值作为月数据,1978年7月份的缺失数据采用线性插值获得,而1979年3月缺测数据采用3月份前15天的数据与4月份前15天的数据取均值计算,最后再结合其他月份数据,求得年辐射值。
多元线性回归模型所需气象数据(气温、降水量、能见度、风速等)来自美国国家海洋和大气管理局国家环境信息中心[15]。
1.2 时间序列分析模型
ARIMA是时间序列分析中主要用于非平稳时间序列分析和预测的一种较为成熟的分析方法,又称为Box-Jenkins方法[16]。一般将满足如下条件的模型简记为ARIMA(p,d,q):
(1)
式中,B为延迟算子;Φ(B)为ARIMA(p,d,q)模型的自回归系数多项式,Φ(B)=1-φ1B-φ2B2-…-φpBp;Θ(B)为ARIMA(p,d,q)模型的移动平滑系数多项式,Θ(B)=1-θ1B-θ2B2-…-θ0Bp;at,as为零均值白噪声序列,E(at)表示t时刻白噪声序列值的数学期望,E(Ys,at)表示s时刻模型预测值Ys和t时刻白噪声序列值at的数学期望。特别地,当d=0,ARIMA(p,d,q)模型实际上是平稳时间序列模型ARMA(p,q);当p=0时,ARIMA(p,d,q)模型退化为差分移动平均模型IMA(d,q);当q=0时,ARIMA(p,d,q)模型退化为差分自回归模型ARI(p,d)。
ARIMA模型实质是将自平稳时间序列模型ARMA(p,q)和差分运算相结合,该模型能够更好地拟合非平稳时间序列。如果自相关和移动平滑部分有缺省,则ARIMA模型可简写为:
ARIMA((p1,…,pm),d,(q1,…,qm))
。
(2)
本文采用的时间序列分析软件为SAS(statistical analysis system),SAS系统具有全球一流的数据仓库功能,在进行时间序列分析时具有其他统计软件无可比拟的优势[17-18]。
2 结果与讨论
2.1 时间序列数据预处理
一般地,需要对时间序列的平稳性和纯随机性进行检验,根据检验结果,确定要采用的拟合预测模型。时间序列的平稳性检验,一般采取时序图检验和构造统计量进行假设检验两种方法。图1为1961—2016年济南市太阳年辐射量的时序图,由图1可见原时间序列具有明显的波动性,自1961—1990年呈显著的下降趋势,1990—2016年较为平稳,但总体呈上升趋势,因此需进一步进行统计检验。

图1 1961—2016年济南市太阳年辐射时序图Fig.1 Time series data of solar radiation at Jinan station during 1961 to 2016
单位根检验是构造统计量进行序列平稳性检验最常用的方法,其统计量有很多,ADF(augmenteddickey-Fuller test)检验是其中经典、简单的一种,也称为增广Dickey-Fuller检验。ADF检验有三种类型的单位根检验模型,具体结构见表1。可见,原序列的检验结果中虽然零均值回归结构的P值大于显著性水平0.05,但单均值和趋势类型中各种延迟模型的Tau统计量(τ)的P值小于显著性水平0.05,据此可判断,该时间序列平稳,且该序列的确定性部分可以用常数均值或趋势类的各种延迟模型结构进行拟合。也就是说,对济南市1961—2015年地表太阳辐射序列的拟合与预测,可采用平稳时间序列模型ARMA或带有趋势的非平稳时间序列模型ARIMA。
进一步对原始序列做一阶差分,发现序列值在0附近波动,呈现出明显的平稳性特征(图2),且差分后ADF单位根检验值(表1)显示,三种类型的检验模型下τ统计量的P值远小于显著性水平0.05,这表明济南市年太阳辐射序列经一阶差分,消除线性趋势后为平稳序列。

表1 ADF单位根检验Table 1 ADF unit root test

图2 1961—2016年济南市地表太阳辐射差分时序图Fig.2 Time series data of differential solar radiation at Jinan during 1961 to 2016
时间序列的白噪声检验一般采用LB统计量(L),如式(3)所示。
,
(3)
式中n为序列观测期数,m为延迟期数。LB统计量近似服从自由度为m的卡方(χ2)分布,同时计算差分前后的LB统计量,检验结果如表2所示。给定显著性水平α=0.05,各延迟期数的LB统计量的P值均小于α,判定该序列在差分前后均是非白噪声序列。结合平稳性检验的结果,我们可以认为济南市地表太阳辐射原序列与差分后序列均是平稳非白噪声序列。

表2 济南市年太阳辐射序列的白噪声检验Table 2 White noise examination of annual solar radiation series in Jinan
2.2 时间序列模型的建立
2.2.1 模型的初步识别
对平稳非白噪声序列建模,通过对该序列的样本自相关系数(ACF)和偏自相关系数(PACF)的分析,初步确定模型的阶数,即p,q的取值。
首先对地表太阳辐射原序列进行分析。由图3(a)(b)可见,ACF基本呈指数衰减,是一种比较典型的拖尾特征,而PACF值延迟一阶以后快速减小至2倍标准差范围以内,但在五阶时PACF值突然升高至2倍标准差范围以外,之后又快速减小至0附近,显示出截尾特征,因此可以初步判断该模型为AR(5)。
一阶差分后时间序列的相关分析如图3(c)(d)所示,自相关系数ACF值呈现四阶截尾,偏自相关系数PACF值呈现一阶、二阶和四阶拖尾,因此可初步判定该差分后的时间序列可用ARIMA(4,1,4)拟合序列。

图3 1961—2015年济南市年太阳辐射序列自相关和偏自相关图Fig.3 Autocorrelation and partial autocorrelation of annual solar radiation series in Jinan during 1961 to 2015
进一步选择贝叶斯信息BIC准则,取p∈[0,5]和q∈[0,5],选取使BIC达到最小的(p,q)组合来分别确定差分前后最优的模型阶数,SAS输出结果见图4。对原样本时间序列,当(p,q)=(5,0)时,BIC值为11.04达到最小值(图4(a)),故最佳拟合模型为ARMA(5,0)模型,即AR(5)模型。对差分后的时间序列,取p∈[0,5]和q∈[0,5],各(p,q)组合下BIC值结果见图4(b)所示。当(p,q)=(4,0)时,BIC值为11.13达到最小值,故最佳拟合模型为ARIMA(4,1,0)。
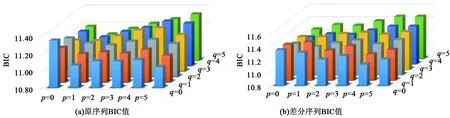
图4 不同(p, q)组合下的BIC值Fig.4 BIC value with different values of (p, q) in models
2.2.2 疏系数模型的建立
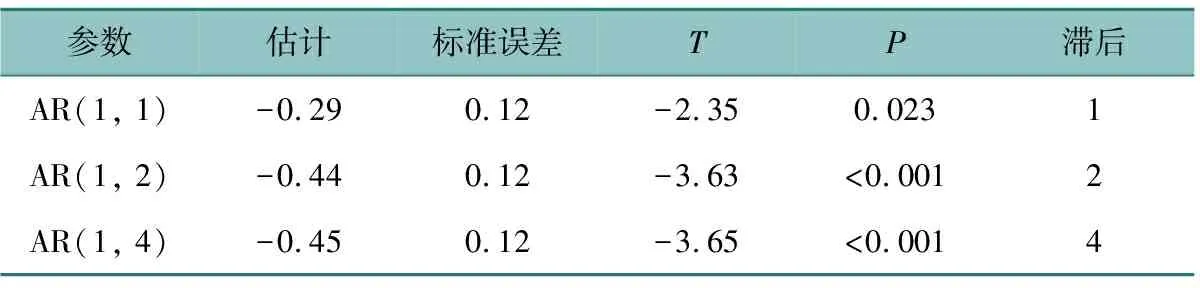
对建立的AR(5)模型,使用条件最小二乘法对模型参数进行检验,同时考虑到拟合模型残差的性质,对模型进行残差检验,检验结果如表3所示。取α=0.05,参数φ2的P值大于0.05,未通过检验。
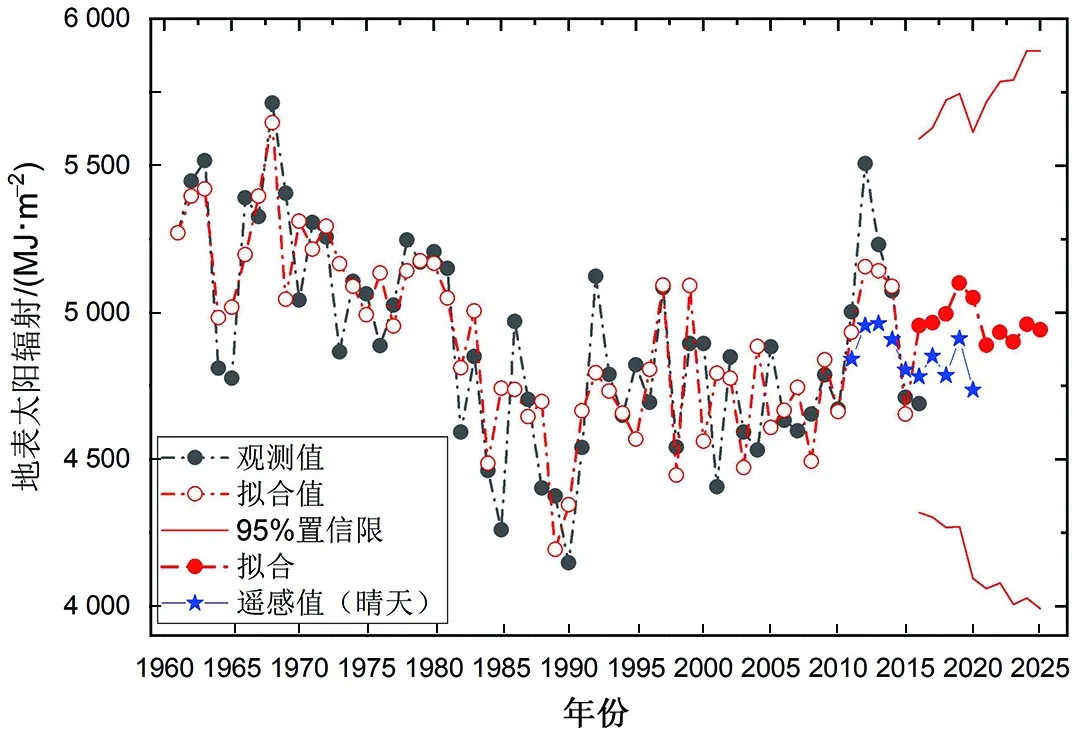
同时,对建立的ARIMA(4,1,0)模型参数和残差进行统计检验,检验结果如表3所示。取α=0.05,残差检验结果显示残差序列为白噪声序列,参数显著性检验结果显示φ1、φ2和φ4的P值均小于0.05,通过检验,但φ3和μ的P值大于0.05,未通过检验。如果ARIMA模型中有部分自相关系数φj(1≤j 表3 ARIMA(4,1,0)模型参数检验Table 3 ARIMA(4,1,0) model parameter test 2.2.3 疏系数模型的检验 对疏系数ARIMA((1,2,4),1,0)模型进行参数显著性检验,结果如表4所示。根据条件最小二乘法估计可知P值小于0.05,故ARIMA((1,2,4),1,0)模型的参数检验通过。 表4 ARIMA((1,2,4),1,0)模型参数检验Table 4 ARIMA((1,2,4),1,0) model parameter test 进一步对疏系数ARIMA((1,2,4),1,0)模型做残差正态诊断,结果如图5所示,其中核表示拟合的ARIMA((1,2,4),1,0)模型中残差的核密度函数曲线。由图5中的残差分布图及其正态QQ图知该残差序列基本呈零均值正态分布,满足残差假定。 图5 残差正态诊断Fig.5 Residual normal diagnosis 综上,ARIMA((1,2,4),1,0)模型通过检验,且修正后的模型为: , (4) 其中B为延迟算子,εt为白噪声序列。 首先对ARIMA((1,2,4),1,0)模型的拟合效果进行验证,与济南市1961—2015年的年辐射观测值相比,模型拟合结果与观测值较为吻合(图6),除个别年份,如1986年、1992年、2012年拟合值较观测值偏低,1964—1965年及1985年拟合值略高于观测值。需要指出的是,部分年份观测值和拟合值之间相对大小趋势存在较大差异,如1970、1971、1975、1985、2000—2005等年份,观测值为极大(或极小)时,拟合值恰为极小(或极大)。分析原因发现,当天气状况不太稳定,阴雨天气比较多,降雨量年间变化比较剧烈的年份,地表太阳年总辐射会产生较大波动,模型的拟合效果也较差,而良好天气状况下年总辐射比较稳定的年份,拟合结果比较精确,这与文献[19]研究结果相似。如1985年降雨量约为708 mm,而1986年降雨量降为344 mm左右;2000—2004年5年平均降雨天数为108天,远高于1980—2016年平均降水天数(78天)。总体上,模型观测值与拟合值的多年平均相对误差为3.1%,多年平均的均方根误差约为192 MJ/m2。这表明该模型可用于济南市年辐射的预测。 图6 济南市1961—2025年ARIMA((1,2,4),1,0)模型拟合地表年辐射值及预测结果Fig.6 ARIMA((1,2,4),1,0) modeling results of annual global solar irradiance at Jinan City during 1961 to 2025 模型预测结果显示:2017—2025年济南市太阳总辐射年平均值约为4 980 MJ/m2,2017—2020年辐射值均高于2021—2025年辐射值(图6)。为进一步验证说明预测结果的可靠性,本文采用遥感晴天下行总辐射数据对比,结果显示,ARIMA预测值的变化趋势与遥感数据较为吻合。 地表太阳总辐射不仅受人类活动、大气污染、降水、云量与风速等因素影响[4-5, 20],同时也与观测站位的迁站、海拔高度、周围遮挡物环境等诸多因素有关[21],且在不同时段主要影响因素也不同,如华东地区太阳辐射1961—1989年的主要影响因素是气溶胶,而在1990—1999年和2000—2008年主要影响是云量[1]。早期研究发现,山东省地表太阳辐射1961—2012年间整体呈下降趋势[22-25]。王建源等[24]发现2001—2007年山东省年总辐射比前30年平均减少72.3 MJ/m2。薛德强[26]认为济南市1961—1990年大气污染物的增多对地表太阳辐射量的减少起着决定性的作用。本文的数据分析显示,自1992年以来,济南市地表太阳总辐射呈持续增大趋势(图1),这可能与济南站的迁站有一定原因。此外,我们发现,2012—2016年济南市地表总辐射平均值较前20年平均增加287 MJ/m2(图6),这可能与近年来山东省各项大气污染防治措施逐步完成并发挥作用,空气质量得到极大改善有关。未来,随着大气环境质量的进一步改善,地表总辐射整体将继续呈增长趋势(图6)。 为对比分析ARIMA模型预测效果,本文使用多元线性回归方法[27-28],利用平均气温(X1)、平均最高气温(X2)、平均最低气温(X3)、平均露点温度(X4)、降水量(X5)、最大单日降水量(X6)、降水天数(X7)、平均能见度(X8)、平均风速(X9)、平均站点气压(X10)10个变量构建线性回归模型: Yt=1 613.30X1t-634.92X2t-1 028.40X3t-73.12X4t-0.039X5t+0.89X6t-2.41X7t+97.31X8t -55.59X9t+30.35X10t-27 379.10 (6) 选择1980—2015年的太阳辐射数据进行检验,结果如图7所示。整体上,多元线性回归模型多年平均相对误差为4.2%,多年平均均方根误差约为201 MJ/m2。与ARIMA((1,2,4),1,0)模型效果相比,误差偏大,但就变化趋势的拟合效果而言,多元线性回归模型优于ARIMA模型,这可能是由于多元线性回归模型考虑了降雨量等因素。 图7 济南市1980—2015年线性模型地表年辐射值及预测结果Fig.7 Linear model annual surface radiation values and prediction results during 1980 to 2015 in Jinan City 本文采用ARIMA模型直接预测的方法,建立ARIMA((1,2,4),1,0)疏系数模型,预测了10年的太阳年总辐射量。对比多元线性回归模型,误差分析表明该ARIMA模型的预测精度更高。预测结果显示,2017—2025年地表太阳总辐射量将保持较为平稳的增长趋势,可加强对太阳能资源的利用。

2.3 地表太阳辐射年际变化的分析及预测
2.4模型对比

3 结语
