高压直流XLPE绝缘电缆载流量的数值算法及特性分析

2023-02-25关健昕欧阳本红黄凯文赵健康严有祥

绝缘材料 2023年1期

赵鹏，关健昕，欧阳本红，黄凯文，赵健康，严有祥

（1.中国电力科学研究院有限公司电网环境保护国家重点实验室，湖北武汉 430074；2.国网福建省电力公司厦门供电公司，福建厦门 361006）

0 引言

直流输电技术在大型新能源发电并网、各大电力系统互联以及海岛供电等方面具有很大优势，使得直流输电装备得到了长足的发展[1]。高压直流电缆作为直流输电系统中的重大装备，是支撑向负荷中心供电和长距离跨海输电的重要部分[2-4]。载流量是电缆传输能力的重要指标[5-7]，直接影响高压直流电缆的运行可靠性和经济性。

长期运行导体温度是决定电缆载流量的核心因素，研究人员对电缆传热模型进行了大量研究，通过电缆表面温度计算导体温度，为电缆运行载流量控制提供依据。如刘刚等[8]通过红外热像仪测量电缆表面温度，进而建立传热数学模型，反演计算导体温度等。近年来，数值分析的发展为计算电缆温度分布提供了便利[9-11]，其中利用有限元法计算温度场已较为成熟[12]。

与交流电缆不同，直流电压下电缆中的电场由绝缘材料的电导率决定，受电场和温度影响，XLPE绝缘材料电导率的变化可能达到2～3个数量级，会直接导致电场分布的反转。因此，直流电缆中的电场分布是决定载流量计算的重要因素，需要考虑电缆的实际运行条件和电-热场耦合计算[13]。郝艳捧等[14]同时考虑了导体最高长期允许温度和绝缘层最大允许温差两个因素，并给出了两种条件下的稳态载流量曲线；阳林等[15]通过有限元法仿真研究了直流电缆温度分布和载流量的关系；王雅妮等[16]研究了多种敷设环境下高压直流电缆的温度分布。但是，有限元法需要建立复杂的直流电缆截面模型，且有大量数据冗余，无法与现有的载流量分析系统相容，在应用上存在很大的局限性，需要提出更加简单有效的电场分布解析计算方法。

本研究基于直流电缆绝缘泄漏电流连续性原理，根据电场分布的特点，引入等效电导率解决绝缘层电场分布计算的电-热场耦合问题；以工程应用的±535 kV XLPE绝缘直流电缆为例，同时考虑电缆导体最高运行温度和绝缘层最大允许温差，计算不同条件下直流电缆负载能力和基于临界环境温度的直流电缆载流量控制域，并分析载流量的影响因素和优化提升方向。

1 电场计算模型

1.1 直流电缆计算模型

高压电缆屏蔽的电导率远大于XLPE绝缘材料的电导率，设置内屏蔽与导体等电位，外屏蔽为地电位，构建如图1所示的计算模型，以求解单一介质XLPE绝缘中的电场分布。其中，电缆导体半径为r1，绝缘层半径为r2，电压为U0，XLPE绝缘的电导率为γ，介电常数为ε。由于正常运行时，电缆中泄漏电流密度很小，可以忽略泄漏电流引起的绝缘层温度变化。

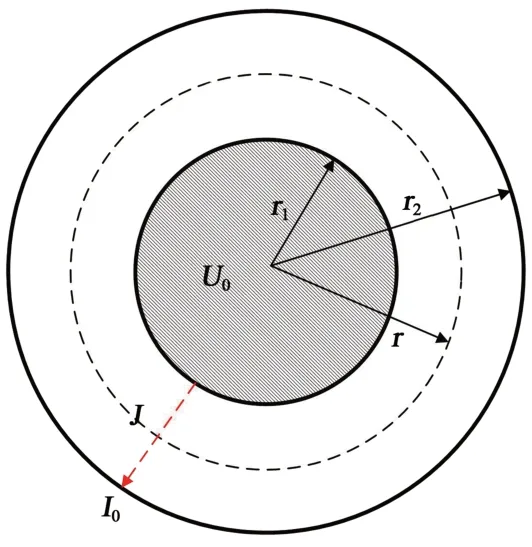
图1 高压直流电缆计算模型Fig.1 Calculation modelling of HVDC cable

文献[17]中提出了在电导率与温度T成指数函数时，绝缘层中电场的推算过程。研究表明，XLPE绝缘材料的电导率与温度的倒数1/T成指数函数[18]，如式（1）所示。

式（1）中：γ为电导率，S/m；T为温度，K；E为电场强度，V/m；a为与材料有关的常数，S/m；b为场强系数为活化能，eV；q为电子电荷量，C；kb为玻尔兹曼常数，J/K。设电导率温度系数c为式（2）。

则可得到式（3）。

设导体温度为T1，外屏蔽层温度为T2，绝缘层温差为Δθi，则绝缘内部温度分布可表示为式（4）[14]。

根据温度分布、电导率函数和电缆结构，可以构建直流电缆电场数值分析基础模型。

1.2 电导率模型

采用两种高压直流XLPE绝缘料开展电导率特性分析，分别为绝缘料A和绝缘料B。电导率测试采用±535 kV直流电缆绝缘先环切成厚度为0.2 mm的长条，再裁剪成尺寸为100 mm×100 mm×0.2 mm的片状试样。为消除切片过程中引入的机械应力，需对试样进行预处理，即在70℃下恒温干燥24 h，然后在环境温度下自然冷却。

直流电导率测试采用三电极系统，以防止测量时表面电流对实验结果产生影响。分别在10、20、30、50 kV/mm电场强度下选取6个不同的温度测试点，开展绝缘试样的电导率测量，记录试样在施加电压30 min过程中的电流曲线。根据电流测量结果的中值，结合施加电压与电极尺寸计算出体积电导率。图2为不同电场下两种绝缘材料的电导率及根据公式（3）得到的拟合曲线。

从图2可以看到，不同电场下拟合曲线与测试结果比较相符，拟合相关系数的平方值R2均不小于0.98，同时得到电导率函数中各项系数拟合结果，如表2所示。从表2可以看出，绝缘料A的电导率温

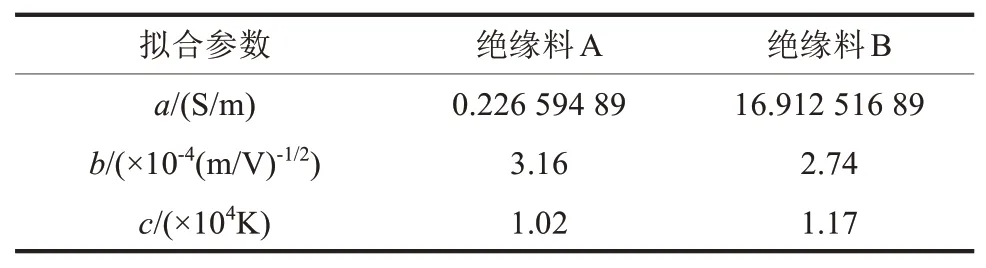
表2 XLPE绝缘材料的电导率拟合结果Tab.2 Conductivity fitting results of XLPE insulating materials

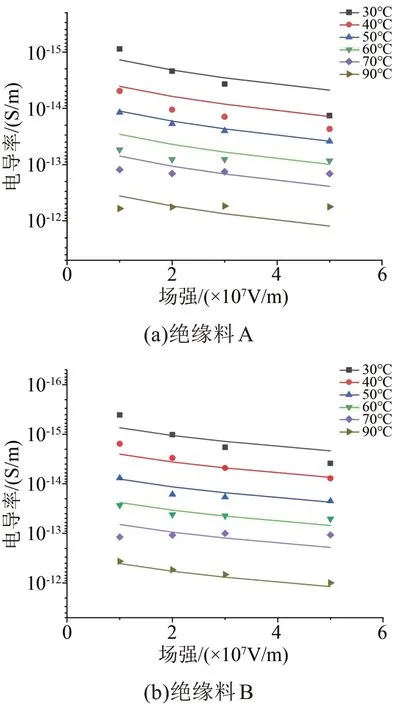
图2 XLPE绝缘材料的电导率拟合曲线Fig.2 Conductivity fitting curves of XLPE insulating materials

度系数c较小，表明采用绝缘料A的直流电缆绝缘层电场分布受温度的影响更小。

1.3 电缆传热模型

稳定运行条件下，单芯直流电缆本体和周围媒介的传热过程可用热路模型等效，则可得直流电缆的载流量计算公式如式（5）所示。

式（5）中：I为直流电缆稳态载流量，A；H1、H2、H3和H4分别为直流电缆绝缘层、阻水层、外护层和外部环境的等效热阻[19]，TΩ/m；RDC为单位长度导体在最高长期允许温度下的直流电阻，Ω/m；θc和θa分别为电缆导体温度和环境温度，℃。

直流电缆运行中只考虑导体损耗，而导体损耗产生的热流向外传输过程中，在不同电缆结构层上产生温差，各层温差取决于导体发热功率和电缆结构层热阻。因此，稳态载流量可以通过绝缘温差和绝缘层的热阻进行计算，等效计算公式如式（6）所示。

结合式（6）可以认为，直流电缆稳态载流量的平方I2与绝缘层温差成正比，即绝缘最大温差可以决定直流电缆的载流量。

2 绝缘电场与最大温差分析

以工程中应用的±535 kV直流电缆为例，分析其电场分布和载流量特性。±535 kV直流电缆的导体截面为3 000 mm2，平均场强为17.83 kV/mm，绝缘设计场强为23.6 kV/mm。电缆其他结构尺寸及热阻系数见表1。

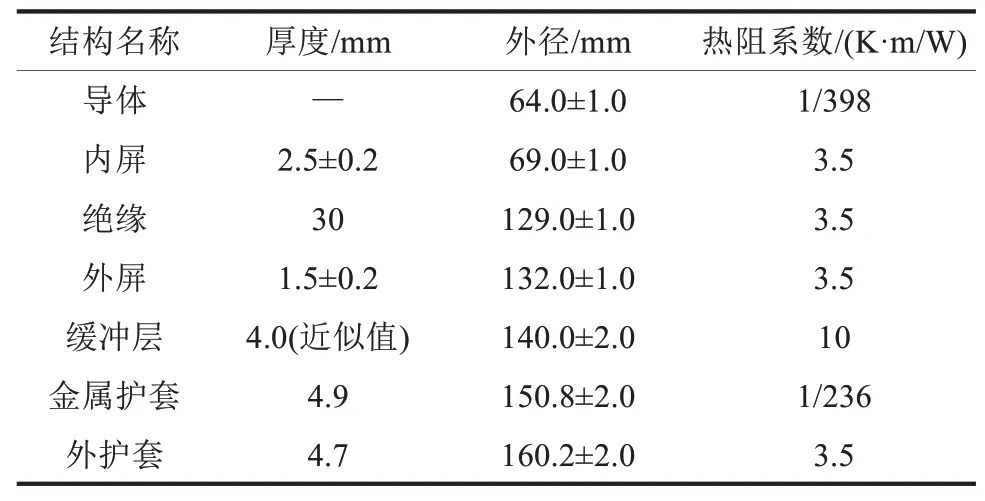
表1 ±535 kV直流电缆结构尺寸及热参数Tab.1 Structure and thermal parameters of the±535 kV HVDC cable

2.1 等效电导率

通过有限元仿真得到不同绝缘层温差下，基于绝缘料A的±535 kV高压直流电缆（简称“A绝缘电缆”）本体绝缘中电场分布，如图3所示。

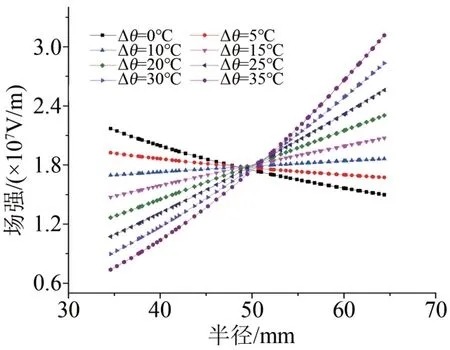
图3 不同绝缘层温差下±535 kV电缆绝缘层中场强分布Fig.3 Electric field distribution in ±535 kV cable under different temperature gradients of insulation layer

在不同绝缘层温差下，直流电缆中电场最大值出现在绝缘内、外侧，而绝缘层中间的电场几乎为定值，且约等于绝缘层的平均场强Eavg。则根据式（7）～（8）所示泄漏电流连续性条件，可得到绝缘泄漏电流值为式（9）。

式（9）中：γavg为等效电导率，代表在绝缘层中间点上的电导率；ravg=1/2(r1+r2)。

等效电导率模型可以简化绝缘层电场分布的计算过程，只需关注绝缘层温度T的变化，则电导率函数模型可以表示为式（10），其中，可以实现电-热均解耦计算。

根据温度分布计算公式（4）和泄漏电流连续性计算公式（9），可以得到绝缘层中间点上的温度Tavg，由此得到不同温度梯度下绝缘层内、外侧的电场强度。

2.2 绝缘电场和最大温差

图4为导体最高运行温度分别为70℃和90℃时，不同温差下绝缘层内、外侧的电场分布。从图4可以看出，基于绝缘料B的电缆内外侧场强随绝缘层温差的变化更大。

实际运行中当直流电缆绝缘层的电场强度最大值等于设计场强时，绝缘层存在最大温差Δθi,max。则可根据图4，得到不同导体温度下直流电缆的绝缘最大温差如表3所示。

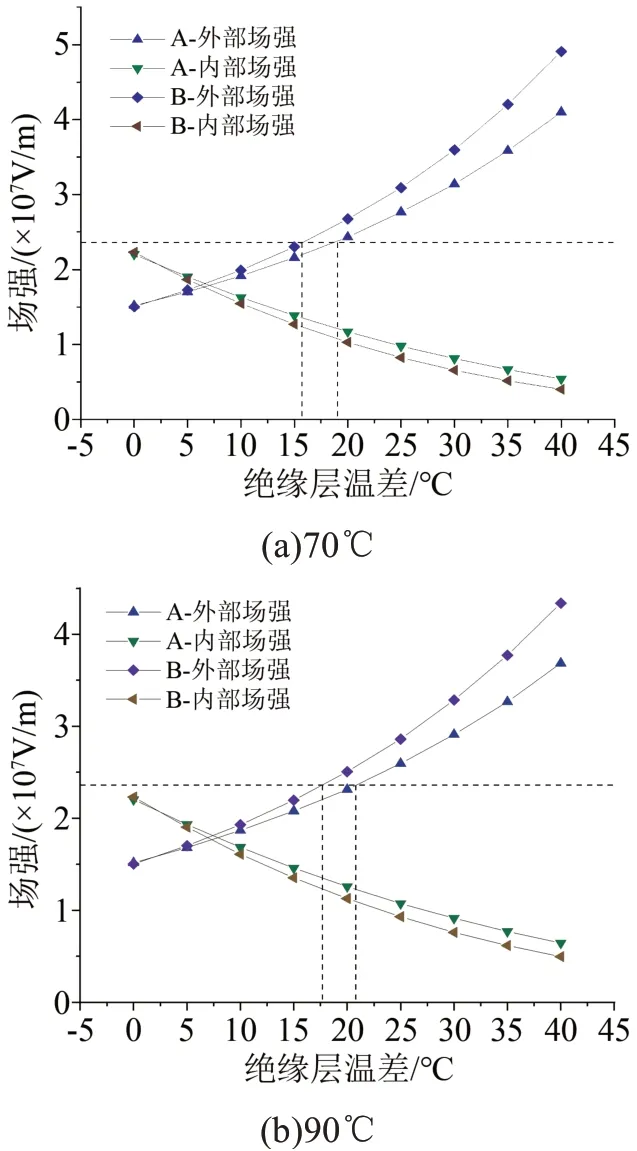
图4 不同绝缘层温差下电缆绝缘层内外侧电场Fig.4 Electric field on the inside/outside of the insulation layer under different temperature gradients of insulation layer

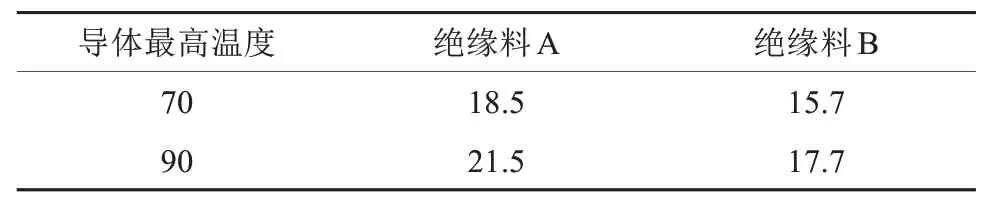
表3 设计场强下电缆绝缘层最大温差Tab.3 Maximum temperature difference of cable insulation layer under design field strength℃

3 直流电缆载流量特性

直流电缆载流量主要取决于导体最高工作温度θc,max和绝缘B最大温差Δθi,max，下面将分别开展不同导体最高温度下电缆的载流量特性分析。

3.1 负载控制域

直流电缆负载安全控制域如图5中阴影部分所示[14]，两条限制曲线和环境温度组成的二维平面上限定了电缆运行中稳态负载的允许范围。在安全控制域内，导体温度和绝缘层温差均满足设定条件。在非安全域I内，导体温度较低，但绝缘层温差超过了允许值；在非安全域II内，导体温度和绝缘层温差都大于允许值；在非安全域III内，导体温度超过了允许值。

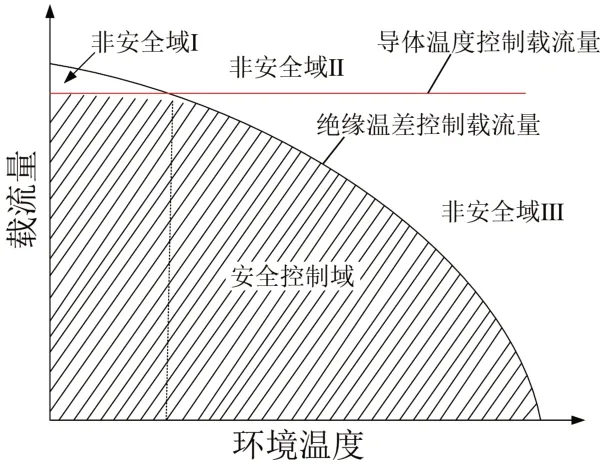
图5 高压直流XLPE绝缘电缆负载控制域Fig.5 Load control domain of HVDC XLPE cable

直流电缆运行中存在稳态负载的临界控制点，其由临界环境温度θa,c和最大负载能力Imax共同确定，即（θa,c，Imax），在临界环境温度以下载流量由绝缘层温差决定；在临界环境温度以上，载流量由导体温度决定。负载控制域的面积决定了直流电缆的输送能力和环境适应性，是评价直流电缆载流量特性最直观的参数。

此外，在电力电缆工程运行中，载流量是综合考虑最高环境温度和导体最高长期运行温度得到的电缆最大负载能力。通常空气中敷设电缆的最高环境温度为40℃，土壤中直埋敷设电缆的最高环境温度为25℃[20]。

3.2 导体最高温度为70℃时的载流量

导体最高温度为70℃的直流电缆负载控制域如图6所示。从图6可以看出，在导体最高运行温度为70℃时，A绝缘电缆的临界控制点为（35.4℃，2 710 A），B绝缘电缆的临界控制点为（42.5℃，2 432 A），差异主要来源于绝缘材料的电导率温度系数不同导致的绝缘最大温差的不同。B绝缘电缆的电导率温度系数更大，使得场强出现较大反转，更小的绝缘温差限制了直流电缆的最大负载能力。

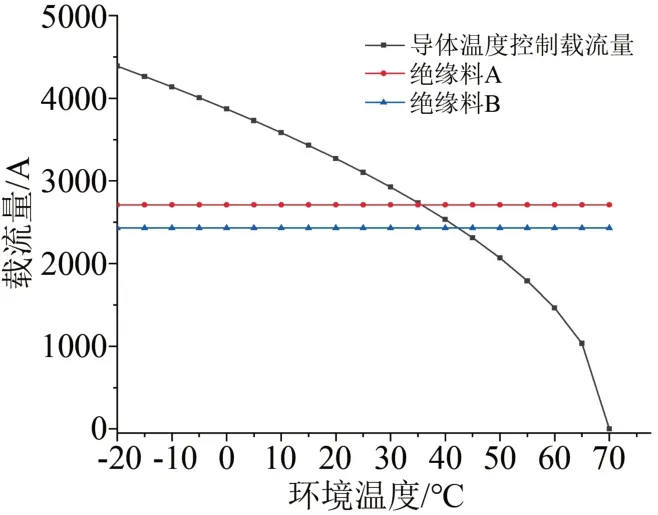
图6 导体最高温度为70℃的直流电缆负载控制域Fig.6 Load control domain of DC cable with maximum conductor temperature of 70℃

分析可知，A绝缘电缆的临界环境温度为35.4℃，低于工程运行中40℃的要求，因此稳态载流量略小于Imax，为2 500 A；B绝缘电缆的临界环境温度为42.5℃，略高于工程运行中40℃的要求，因此稳态载流量即可设定为Imax，即2 432 A。

3.3 导体最高温度为90℃时的载流量

导体最高温度为90℃的直流电缆负载控制域如图7所示。从图7可以看出，在导体最高运行温度为90℃时，A绝缘电缆的临界控制点为（54.2℃，2 705 A），B绝缘电缆的临界控制点为（60.0℃，2 471 A）。根据表3，导体最高温度为90℃时，绝缘最大温差较导体最高温度为70℃时更高，但计算结果显示最大负载能力Imax与70℃时差别不大。这是由于导体电阻变大会增加线路损耗，限制了电缆传输的最大负载能力Imax。

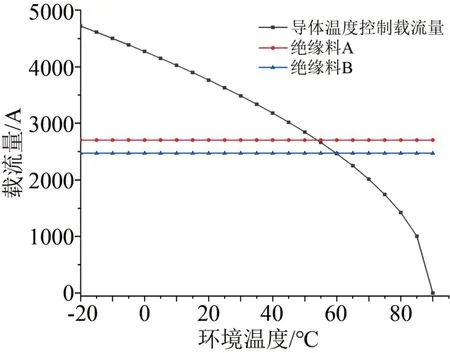
图7 导体最高温度为90℃的直流电缆负载控制域Fig.7 Load control domain of DC cable with maximum conductor temperature of 90℃

与导体最高温度为70℃的情况相比，导体最高温度为90℃时临界环境温度变化很大，表明直流电缆在环境温度为54℃以下时，最大负荷均受温度梯度限制，即载流量为最大负荷能力Imax，而这种传输能力显然是不够经济的，实际工程中，直流电缆也很难应用于为40℃以上的环境温度。

3.4 讨论

直流电缆载流量的确定需要综合考虑临界环境温度和最大运行环境温度。其中，临界环境温度θa,c可通过数值计算方法准确得到，是表征电缆最大负载能力的重要特征参数。对于隧道敷设的直流电缆，如果临界环境温度θa,c＜40℃，则稳态载流量I小于最大负载能力Imax；如果临界环境温度θa,c≥40℃，则稳态载流量I等于最大负载能力Imax。

临界环境温度θa,c取决于导体最高运行温度。按照IEC 62895:2017要求，±535 kV直流电缆的导体运行最高温度由制造商申明，目前主要包括70℃和90℃两种，根据分析，将导体最高运行温度提高20℃时，临界环境温度θa,c几乎同样提升了20℃，使得A绝缘电缆可以在40℃条件下达到最大负载能力Imax，载流量受绝缘层最大温差控制的环境温度范围增大，但是总体上Imax并未改变，其关键在于绝缘最大温差是由设计场强和电场分布共同决定的，取决于绝缘材料的介电性能，并不随导体的最高运行温度升高而发生较大变化。

如果不改变绝缘材料性能，通过导体最高运行温度难以提升直流电缆的载流量。对于±535 kV直流电缆，当导体最高运行温度由70℃提升至90℃时，单位长度电缆导体的直流电阻RDC从6.86×10-6Ω/m提升至7.31×10-6Ω/m，在同样的负荷条件下，增加的导体损耗也需要更大的绝缘层温差，此外，当导体最高温度提高后，高温高场强下直流电缆绝缘电导机制更容易由体（Poole-Frenkel）效应转变到电极（Schottky）效应[21]，会增加绝缘层电场的反转。从经济性考虑，仅提升直流电缆最高运行温度对于提升载流量作用有限。

直流电缆设计场强受绝缘材料的长期老化寿命指数n影响，按照40年的长期运行要求，电缆本身的绝缘缺陷，包括气隙、杂质以及界面突起等均会使寿命指数降低，因此提升绝缘设计场强的关键在于提升绝缘材料的耐电性能。直流电缆的电场分布由绝缘材料的电导率温度特性决定，优化绝缘材料的电导率温度特性，改善绝缘层温差下的场强反转，可以保证在同样的设计场强下允许更大的绝缘层温差。对于实际工程，建议将直流电缆负载控制域和临界控制点纳入供应商应当掌握的关键参数中[22]，而且临界环境温度θa,c越接近敷设最大环境温度，则对电缆运行和设计越经济。