深部含水层储热系统的数值模拟研究

黄永辉 , 杨俊生 , 朱传庆 , 孔彦龙

1)中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249;2)中国石油大学(北京)地球科学学院, 北京 102249;3)中国科学院地质与地球物理研究所, 北京 100029

含水层储热系统是指将多余的能量(例如: 风能/太阳能/工业余热)转化为热水的形式存于地下含水层中的储能技术(Tsang et al., 1981; 薛禹群等,1989)。含水层储能具有储量大、成本低、跨季节等优势, 可以弥补能源供需在时间/空间分布的不平衡, 能够综合利用多种可再生能源形式,减少对矿物燃料的依赖, 实现节能减排(汪集旸,2018)。

与传统的水热型地热系统类似, 含水层储热系统通常以对井形式存在, 分为冷井和热井。夏季通常作为储热季, 将温度较低的地热水从冷井中抽出,通过剩余的太阳能、风能或者工业余热等外部热源对地热水进行加热(Doughty et al., 1982), 加热后的地热水再注入热井中进行存储; 冬季为开采季, 再将温度较高的地热水从热井中开采出来进行供暖,换热之后的尾水再回灌至冷井中, 至此完成一个储热-取热循环周期(黄永辉等, 2020)。图1是含水层储热的示意图。

图1 深部含水层高温储热系统储能/供能示意图(修改自Kallesøe et al., 2019)Fig. 1 Basic principle of deep-ATES (modified from Kallesøe et al., 2019)

含水层储热系统按含水层深度分类: 可分为浅部含水层储热和深部含水层储热(Lee, 2010), 其中浅部含水层储热通常指将热水存储在500 m以浅的含水层中, 储热温度一般＜50 ℃, 而深部含水层储热的含水层深度通常位于500～3000 m, 储热温度通常 50～150 ℃(Drijver et al., 2012)。

浅部含水层储热研究较为广泛, 我国最早于20世纪60年代即在上海等地区开展了“冬灌夏用”和“夏灌冬用”的浅层含水层蓄热与制冷的相关实践(马捷等, 2004)。截至2017年, 世界范围内已建有2800余座浅部含水层储热系统(Fleuchaus et al.,2018)。近年来, 随着能源需求日益增长, 深部地热储能技术受到了越来越多的关注, 关于深部地热储能技术的研究和工程实践也越来越多。

目前世界范围内关于深部含水层储能系统仍处于理论研究和示范工程阶段(Wesselink et al., 2018)。德国宝马公司和慕尼黑工业大学于2016年设计了一套深部含水层储能系统, 注水温度可达130 ℃, 注入流量在280 m3/h, 含水层选在深度为500 m的石灰岩层; 汉堡市政府已于2017年成功实验利用垃圾焚烧场和污水处理厂的余热, 将水加热至80 ℃并存于地下 400～500 m 砂岩含水层中, 以实现为旧城区居民供暖。瑞士2017年计划在首都伯尔尼地区将发电站的废热存储在地下 500 m砂岩含水层, 以满足冬季市区供暖。近年来, 国内外不断有政府间资助主导的大项目聚焦深部含水层储热技术。自2018年, 欧盟资助了地下储热项目 HEATSTORE(https://heatstore.eu/), 总投资达到 5000万欧元, 共9个国家参与(包括德国、法国、荷兰、瑞士、比利时、丹麦、冰岛等), 项目为期5年(2018—2022年), 共资助6个地下储热示范项目, 其中包括3个深部含水层储热项目。另外美国国家科学基金会(NSF)资助的地下储热项目Geothermal Battery(Green et al., 2021),总投资 1000万美元, 由犹他大学牵头, 美国爱达荷国家实验室联合多家企业参与其中。美国地质调查局于2018年资助的Reservoir Thermal Energy Storage项目聚焦于利用沉积盆地深部储层开展储热蓄冷的示范工程建设我国在深部含水层储能方向的研究开展较晚, 针对深部含水层储能系统的实际工程或示范工程几乎还是空白(张媛媛等, 2021)。

相比浅部含水层储热, 深部含水层储热具有如下优势: 1)储热温度越高, 能量密度越大, 单位体积的经济回报率也更高; 2)深部含水层储热温度通常大于 50 ℃, 用于供暖时可以避免使用热泵进行提温, 极大节省了成本; 3)由于深部含水层储热的目标储层均在500 m以深, 可以避免污染浅部地下水(Burns et al., 2020)。

近年来, 国际上关于深部含水层储能系统的研究集中在如何提升系统性能和储能效率(Huang et al., 2021)。影响深部含水层储热系统的储热性能的关键因素之一是由于传导和对流造成的热损失。前人的研究确定了热损失与含水层和注入流体特性的联系(Kim et al., 2010; Schout et al., 2014), 同时在储热过程中, 由于密度差异流造成的自由对流是造成热量损失的主要因素(Lee, 2010)。Schout et al.(2014)基于跨季节高温含水层储热系统的浮力流与传热过程, 推导了储热效率与瑞利数(Rayleigh number)之间的解析解表达式, 阐释了含水层渗透率、含水层厚度、储热流量、储热温度和含水层初始温度等参数为影响储热效率的重要因素。Collignon et al.(2020)和 Birdsell et al.(2021)进一步研究了含水层渗透率影响储热效率和储热能力的机制, 并认为较高的渗透率会降低储热效率, 而中低渗含水层在储热和取热阶段所允许的注入/开采的热水量通常较小, 以避免造成岩石断裂和破坏整个热储存的损失, 这样大大影响了含水层的储热能力。因此, 在规划深部含水层储热系统时, 需要对系统热损失和储热能力之间的平衡进行评估。

含水层储热项目的可行性由其投资成本、经济收益、系统性能及其对周边环境影响所决定, 因此需要对深部含水层的水文地质和物理特性以及地下水流动传热特性进行精细化描述, 更重要的是正确评估真实储热能力和相关的热损失或储热效率(Huang et al., 2021)。数值模拟方法, 作为一种高效而方便的定量化研究手段, 已经成为国际范围内评估和优化含水层储热项目的标准程序(O’Sullivan et al., 2000; Lee, 2010)。

本文结合我国北方典型地热田碳酸盐岩热储的地热地质概念模型, 利用数学模拟的方法, 评估了一组典型深部含水层储热系统的储热能力和储热效率。分析了关键储层参数对系统性能的影响, 本文的研究旨在为后续开展深部含水层储热系统工程的设计与优化提供科学参考。

1 数值模拟方法

为了研究深部含水层储热系统中渗流传热的规律, 首先考虑描述多孔介质中流体运移过程, 这里采用达西连续性方程作为控制方程:

其中Φ是孔隙度,ρl是流体密度,Q是源汇项,vl是流体流速, 可由达西定律予以描述:

其中K、μ分别对应岩石的渗透率, 流体粘滞系数,p是压强, g是重力加速度。

为了考虑高温作用下传热过程, 考虑能量守恒方程作为控制方程以描述非等温过程:

其中hl是液相的焓,λ是热传导系数,Qheat是热量的源汇项,Ht是系统中总的焓, 包括流体和岩石两部分的贡献,

其中ρR是岩石的密度,CpR是岩石的比热容。

本次数学模型的建立基于开源模拟软件OpenGeoSys。实现传热-渗流多场耦合, 其中高温流体的热力性质通过 IAPWS模型予以描述(http://www.iapws.org/)。耦合模型拟采用 Galerkin有限元法在空间上作离散, 用 Euler差分法在时间上离散, 基于全局隐式耦合算法, 用 Newton-Rapson方法处理耦合方程的非线性, 直接求解器SparseLU用于求解稀疏矩阵。

2 模型设定

本文针对我国北方典型地热田碳酸盐岩热储建立了水-热耦合3-D场地尺度地热模型。地热地质概念模型的参数设定依据雄安新区牛驼镇地热田蓟县系雾迷山组的地质参数进行建立, 具体可参考Wang et al.(2021)中的描述。

模型长度设置为1000 m, 宽度为1000 m, 根据雄安新区牛驼镇地热田热储顶板埋深为800～1000 m(朱喜等, 2022), 假设模型顶部位于地下1000 m深处, 沿垂向厚度为 1000 m, 其中储层厚度 600 m,深度设为1200～1800 m, 同时分别考虑200 m厚的上覆盖层和200 m厚的基岩。为保证计算结果不受网格数量的影响, 对网格进行加密, 直至获得网格无关性计算结果。最终模型区域被剖分为约60 527个网格节点, 338 464个泰森多边形网格, 同时网格在冷井和热井处附近进行局部加密, 如图2所示。

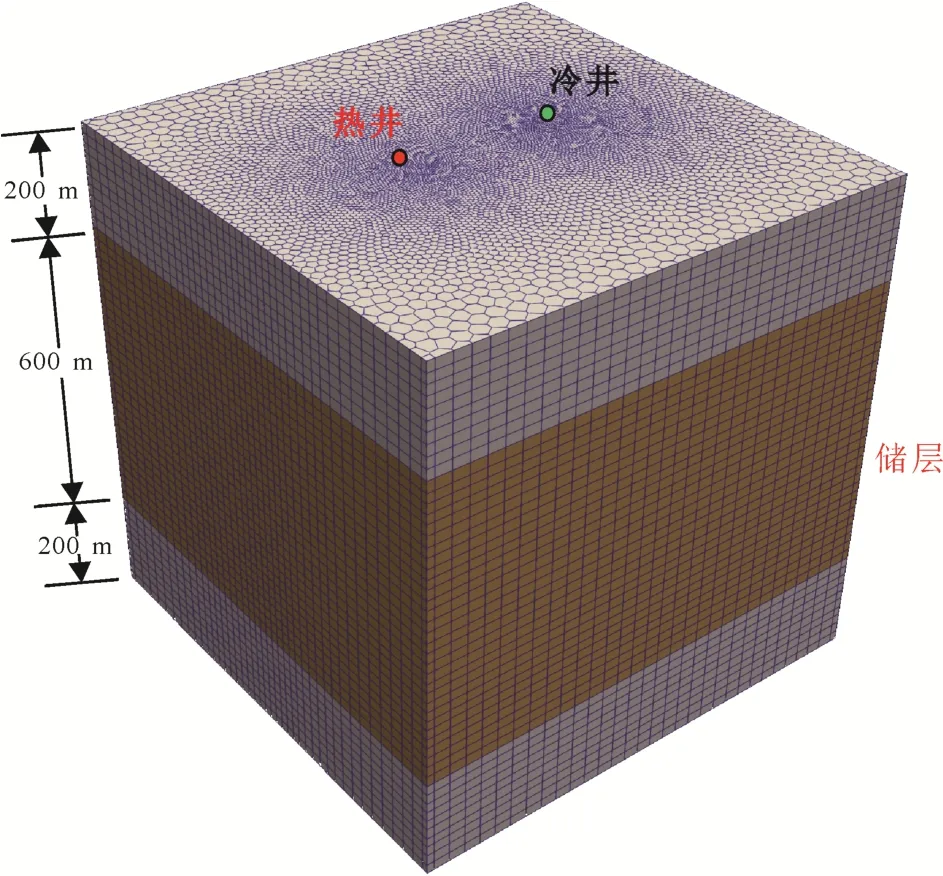
图2 3维模型示意图与网格剖分Fig. 2 Schematic representation of the 3D model and the mesh discretization

模型的初始条件与边界条件的设定: 假设地表温度为0 ℃, 采用如下所示的温度沿深度的分布函数来定义模型的初始温度。

鉴于本研究对深度区间为-1000 m至-2000 m,初始温度延深度的表达式可定义为:

(1) -1000 m至-1200 m的盖层温度可表示为:

(2) -1200 m至-1800 m的储层温度可表示为:

(3) -1800 m至-2000 m的基岩温度可表示为:

Z是储层深度(m),即储层内温度梯度为5.0 ℃·km-1, 在上覆盖层和基岩中, 地温梯度较之更大, 为 50.0 ℃·km-1, 因此达到储层顶部地层温度为50 ℃。地温梯度数据依据牛驼镇地热田实际地温梯度数据设定, 具体参考文献王朱亭等(2019)。

在模型的底部, 采用恒定的基础热流值63.8 mW/m-2(马峰等, 2020; Wang et al., 2021)。储层初始压力在深度方向假设遵循静水压力分布。针对边界条件, 垂直边界距离注入井较远, 因此在侧边界设定零热通量和质量通量的边界条件。

在本研究中, 针对深部含水层储热模型, 假设一个储热-取热周期为一年, 其中储热时间为4个月,紧接2个月的静置时间, 之后是4个月的取热时间,再紧接2个月的静置时间。

依据雄安新区牛驼镇地热田地热井的实际流量数据, 假设热井的注入流量和开采流量保持在一个恒定值, 为120 m3/h, 其中储热温度维持在95 ℃以避免发生相变, 通过数值模型计算出热井的开采温度。冷井的开采和回灌流量也分别设定为120 m3/h, 回灌温度假设为25 ℃。最后, 热井和冷井的平面坐标分别为(350, 500)、(650, 500)。

在模型中进一步考虑到地热流体参数性质随温压的变化规律, 即地热流体的密度ρf和粘滞系数在模型中考虑为随着温度和压力的变化而变化的函数。流体密度与温度、压力的关系如图3所示。

图3 流体密度和粘滞系数随温度、压力变化的关系Fig. 3 Water density (top) and viscosity (bottom) as a fraction of pressure and temperature

模型的其他输入参数已总结在表1中, 模型参数参考文献Wang et al.(2021)。

作为参照对比, 同时考虑一个传统的水热型对井采灌模型, 假设一个采灌周期为一年, 开采期/回灌期为四个月, 剩余 9个月为静置恢复期。其余水文地质参数保持不变, 如表1所示。

表1 模型输入参数Table 1 Model input parameters

3 模拟结果

3.1 温度

由图4可以看到, 在一个周期内, 热井的温度随着开采过程逐渐降低, 但随着循环周期的继续,开采井的最低温度逐年在增加, 而在第 20年后逐渐稳定。对于95 ℃的注水, 在第1个循环后, 生产井的温度从95 ℃下降到了62 ℃, 大约20个循环后的生产井温度从95 ℃下降到大约85 ℃。

图4 深部含水层储热系统中热井(开采井)温度随时间的演化过程Fig. 4 Temporal evolution of the temperature at the warm well in deep-ATES system

在最初的生产/注入周期中, 冷井生产阶段结束时的温度迅速下降, 而在暖井处迅速上升。在热井周围, 随着每个循环, 由于一部分注入的热量没有回收, 这使得热井周围的含水层逐渐变暖。由于温度的升高, 在接下来的开采季, 恢复的温度范围缩小了。而在冷井中发生了类似的过程, 导致冷井周围的储层逐渐冷却。正如之前的研究中观察到的那样, 这种局部变暖和冷却会增加系统的热回收效率。

图5给出了传统水热型地热系统中开采井温度随时间的变化过程, 由图中可以看到, 在传统的水热型对井系统中, 开采井温度随着时间的推移在逐渐下降, 在50年的开采周期后, 开采井温度下降了约 2.5 ℃, 这是由于回灌的冷水锋面在运移过程中到达开采井附近, 发生了热突破, 影响到了开采井的温度。

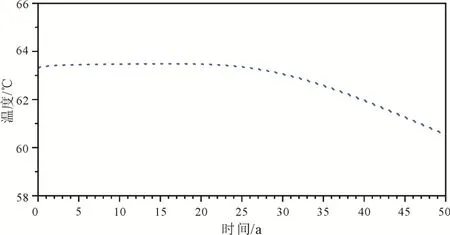
图5 水热型对井地热系统中开采井温度随时间(50年)的演化过程Fig. 5 Temporal evolution of the temperature at the production wells in traditional hydro-thermal doublet system

图6分别给出了第10年和50年开采期结束之后, 深部含水层储热系统与传统水热型对井系统储层中温度场的分布。由图可见, 在深部含水层储热系统中, 在热井周围形成了温度增加的区域, 而在冷井周围, 形成了温度降低的区域。随着系统持续运行, 增温区域和降温区域的面积在不断扩大。这表明热井周围储层由于储热的作用持续的被加热,而冷水回灌导致冷井周围储层温度持续降低, 但从20年后, 受影响的区域范围几乎不再扩大, 趋于稳定, 这是由于热井与冷井周围温度趋于稳定, 如图4所示。

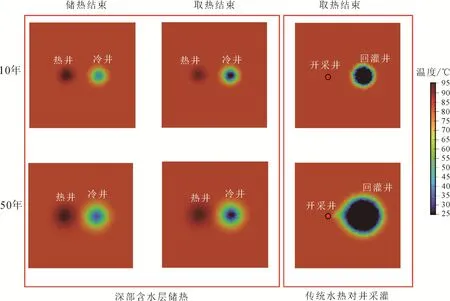
图6 深部含水层储热系统与传统水热型对井系统的温度场分布Fig. 6 Temperature distribution at the end of 50 years operation in deep-ATES system and traditional hydro-thermal doublet system

同时, 从图6中可以看到, 传统水热对井采灌系统中, 由于冷水回灌, 在回灌井周围形成了温度降低的区域, 且随时间增加冷水影响范围越来越大,在50年采热结束后, 冷水锋面达到了开采井处, 发生了热突破。由此可见, 深部含水层储热系统回灌冷水的影响范围面积远小于传统水热型尾水回灌造成的温度下降区域面积。热突破对系统寿命的影响在深部含水层储热系统中被大大减弱。采用深部含水层储热技术有助于热田的可持续开采。

3.2 压力

除了温度变化, 储热、取热过程中井底压力的变化也是研究需要重点关注的内容。因此需要进一步研究热井井底压力随时间的演化过程。如图7所示, 在储热刚开始, 井底压力迅速升高, 之后在整个储热期间, 压力几乎维持不变, 而在开采初期,与之相反, 井底压力迅速下降, 在之后开采阶段井底压力几乎维持不变。

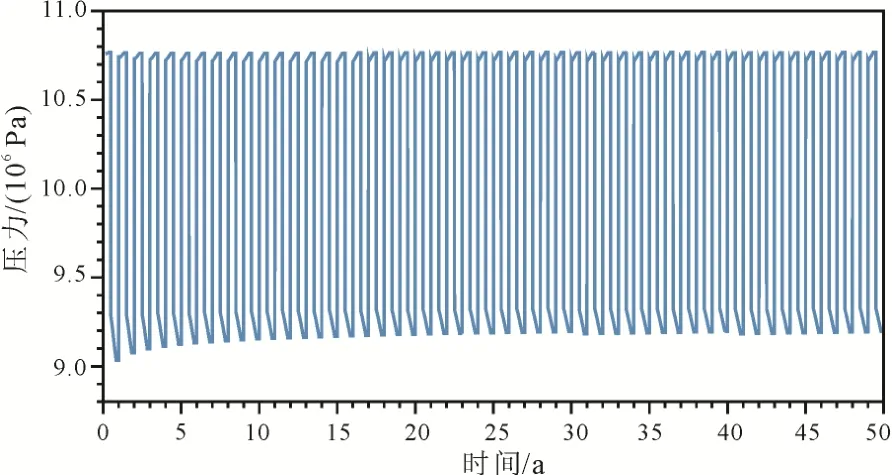
图7 热井井底压力随时间的变化Fig. 7 Temporal evolution of the bottom hole pressre at the warm well in the deep-ATES system

3.3 储热性能和储热效率

接下来重点评估深部含水层储热系统的热性能和储热效率。根据定义, 储热效率η可以按如下公式进行计算(Bloemendal and Hartog, 2018):

其中:Eprod和Einj分别是一个储热/取热周期内开采出来和储进去的热量,tprod和tinj分别是开采时间和储热时间, 而Pprod和Pinj分别是一个储热/取热周期内开采和储热功率, 由下式定义:

其中Q是开采/注入流量,ρf是流体密度,Cf是流体的比热容,是是含水层初始温度。

从图8中可以发现, 系统的储热效率随着时间/循环的累积而增加, 这是由于随着储热的继续, 储层在不断的被加热, 而注入流体温度(即储热温度)和储层之间的温差在不断缩小。而且储热效率在第一个储热/取热循环周期之后提升的最多, 而在第20年后, 储热效率趋于平衡。在本研究的模拟中,第一年的储热效率仅为 60%, 而在第二年提升到70%, 第 20年的时候, 储热效率可以达到 80%, 到第50年的时候, 储热效率接近85%。

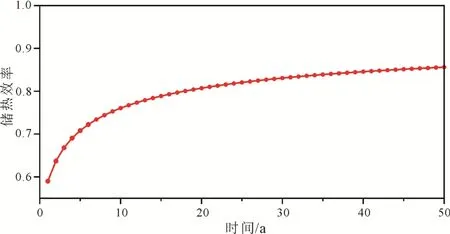
图8 深部含水层储热系统的储热效率随时间变化Fig. 8 Temporal evolution of the energy recovery factor during the deep-ATES exploitation

深部含水层储热系统, 在第一个开采季, 随着开采温度的降低(如图9所示), 取热量从 12.3 MW降低到11 MW, 但随着时间继续, 储层温度在渐渐提升, 在第20年后, 年取热量稳定在12～12.3 MW。而随着地层热量的消耗, 以及回灌尾水热突破造成开采井生产温度的降低, 传统水热型地热系统开采季的取热量随时间逐渐降低。

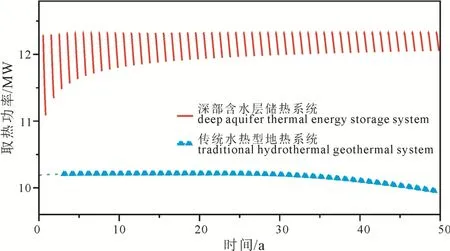
图9 采暖季热能提取功率的对比Fig. 9 Comparison of the thermal recovery power between deep-ATES system and traditional system

模拟结果表明: 在当前模型参数设定的情形下,传统的水热型地热系统(对井模式), 在50年的开采周期内, 年均可开采热能为 10 MW。而深部含水层储热系统, 在50年的开采周期内, 年均可以开采约12.2 MW。相比传统的水热型地热系统, 在开采流量相同的条件下深部含水层储热系统的单井取热量可以提升约20%。

4 参数分析

4.1 储层渗透率

储层渗透率是影响深部含水层储热系统的关键参数。为了进一步分析其影响, 本研究对比了两组不同储层渗透率: 1×10-14和1×10-13m2, 同时在模型中忽略地层的非均质性和各向异性的影响。每组储层渗透率下的储热效率和热井温度随时间的变化绘制于图10和11中。

图10 不同储层渗透率(1×10-14和1×10-13 m2)系统的储热效率对比Fig. 10 Comparison of the recovery factor of the system under different permeabilities(1×10-14 and 1×10-13 m2)

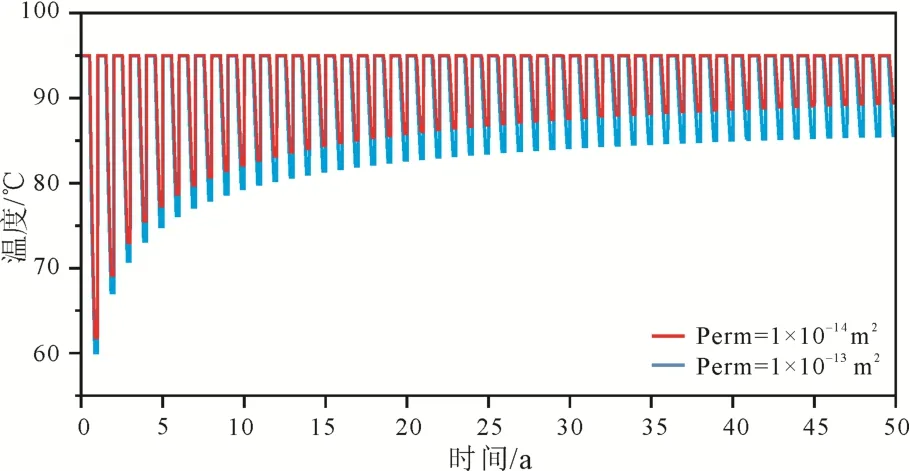
图11 不同储层渗透率(1×10-14和1×10-13 m2)系统的热井温度对比Fig. 11 Comparison of the hot well temperature of the system under different aquifer permeabilities(1×10-14 and 1×10-13 m2)

从图10中可以看出: 当储层渗透率越高的时候, 系统的储热效率越低, 当储层渗透率从 1×10-14加到10-13m2时, 50年的运行后系统储热效率降低了 7%。同时, 从图11中也可以看出, 储层渗透率越高, 开采季中热井的开采温度越低, 当储层渗透率从10-14增加到10-13m2, 50年后开采温度差别大于5 ℃, 这是因为地下水流速会随着储层的渗透性增加而增加, 这样会增强地热流体与周围岩体的热对流, 导致热损失增强。

但另一方面, 随着储层渗透率的增加, 井底累积压力会降低, 如图12所示。这往往允许更大的注入流量, 系统储热能力会得到提升; 同时由于井底累积压力的降低, 流体注入所需消耗水泵的注入功率会降低, 也会降低运营成本。

图12 不同储层渗透率(1×10-14和1×10-13 m2)系统热井的井底压力对比Fig. 12 Comparison of the bottom hole pressures of the system under different permeabilities(1×10-14 and 1×10-13 m2)

因此, 在深部含水层储热系统中, 储层渗透率的选择, 往往需综合考虑储热效率、储热能力和运营成本之间的平衡。

4.2 储热温度

为了进一步研究热井的不同储热温度对储热效率的影响, 本研究对比了两组不同储热期的注入流体温度: 125 ℃和95 ℃情形, 并将每组情形下的储热效率随时间的变化绘制于图13。

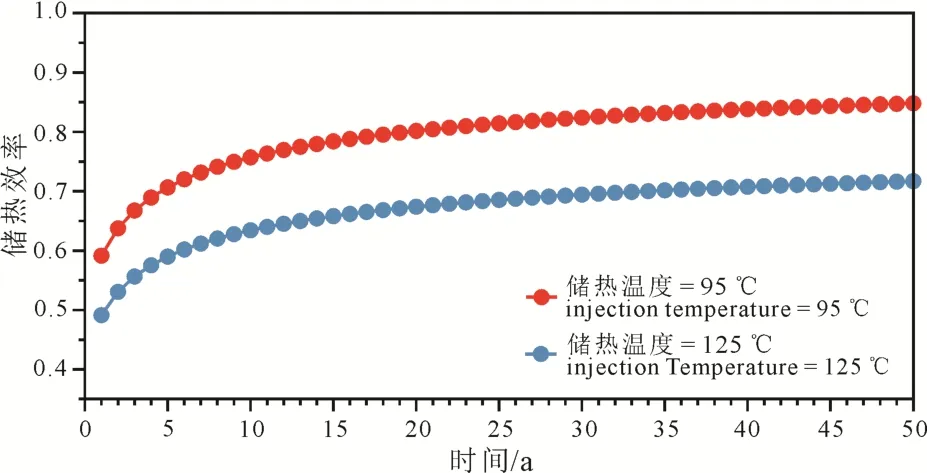
图13 不同储热温度(95 ℃和125 ℃)系统的储热效率Fig. 13 Recovery efficiency of systems with different thermal storage temperatures (95 ℃ and 125 ℃)

从图中可以看出, 储热期的不同注入流体温度对系统的储热效率有较大影响。随着注入流体温度的升高, 系统的储热效率反而降低。

这是因为一方面注入温度越高, 注入流体与储层岩体初始温差就越大, 这样增强了热散失。另一方面, 随着注入流体温度的升高, 注入流体与地层原层流体的密度差以及流体的粘度均增加, 这使得浮力流的影响变得更强, 更多的能量转移到含水层的上部并留在上部, 热对流导致的热散失更明显。

4.3 储层初始温度

为了进一步研究储层不同的初始温度对储热效率的影响, 本研究对比了3组不同储层初始温度:40 ℃, 50 ℃和60 ℃情形, 并将每组情形下的储热效率随时间的变化绘制于图14。

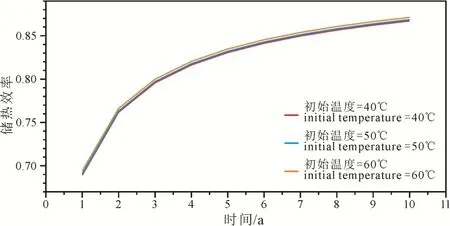
图14 储层不同初始温度(40 ℃、50 ℃和60 ℃)系统的储热效率Fig. 14 Recovery efficiency of systems with different initial temperature of the aquifer (40 ℃, 50 ℃ and 60 ℃)

从图14可以看出, 储层不同的初始温度对系统的储热效率有影响, 但影响较为有限。随着储层初始温度的提升, 系统的储热效率有略微上升的趋势, 但不明显。

5 讨论

传统的水热型地热系统, 对储层地质条件要求至少满足三种条件: 1)储层有足够量的水; 2)储层具有一定的孔渗性, 允许流体的开采和回灌; 3)储层温度要足够高(Randolph and Saar, 2011; Tang et al.,2022)深部含水层储热系统, 较水热型地热系统, 对地质条件的要求较为宽松, 不需要要求储层的温度足够高。采用深部含水层储热系统, 可以对一些温度不高的储层进行增强, 使其满足开采需求。但不可忽视的是, 深部含水层储热系统的运行需要建立在有足够廉价的外部能源的基础上, 例如弃风、弃光或者工业余热等(Fleuchaus et al., 2020)。

需要指出的是, 该研究目前尚存在较多局限性。首先本研究所建立的数值模型为理想模型, 未必能体现实际情况。其次由于获取地热系统温度场和流场的野外监测资料难度大而缺乏详实的观测数据, 同时还受到计算资源的限制, 计算模型及定解条件做了一定简化。目前国内外在深部含水层储热系统数值模拟研究领域中尚存在局限性, 通过数值模拟手段评估并预测地热系统的运行效率及可持续利用性时, 必须结合实际工程情况和地质条件, 评估模型假设条件和简化的合理性, 同时需验证模拟结果的有效性。

6 结论

本文介绍了一种新的水热型地热资源利用的方式: 深部含水层储热技术。本文通过数值模拟的方法, 初步估计了深部含水层储热系统的热性能,并与传统水热型地热系统的取热性能进行了对比。

通过数值模拟的结果表明, 深部含水层储热系统采热量明显高于传统的水热型对井取热系统。通过提高温度的方式, 可以提升单井供热能力 20%。在50年的运行后系统储热效率可以达到85%, 能够保证更高的地热能提取效率; 同时, 深部含水层储热系统可以延长地热井寿命, 避免回灌冷水造成热突破, 实现可持续开采。

通过参数敏感性分析的方法发现, 储层渗透率和储热温度等是影响储热能力和效率的关键参数。本研究为后续开展深部含水层储热系统工程的设计与优化提供科学参考。

Acknowledgements:

This study was supported by National Natural Science Foundation of China (No. 41902311).