基于Stribeck曲线的液压缸劣化趋势评价

蔺凤琴， 于 鹏， 荆丰伟， 赵庆浩， 毕鹏飞， 贾瑞哲， 郭 金

(1.北京科技大学 自动化学院， 北京 100083； 2.北京科技大学 高效轧制与智能制造国家工程研究中心， 北京 100083)

引言

液压系统是由动力元件、执行元件、控制元件、辅助元件(附件)和液压油5个部分组成的复杂动力学系统[1]。由于其具有体积小、刚度大、精度高、响应快和驱动力大等特点，现已被广泛应用于各个行业中，如国防工业、机械农业、冶金工业和轻纺工业等[2]。随着国内制造业和生产业向现代化和智能化转型，各行业对装备精度的要求变得十分严苛，对液压系统的要求也越来越高。液压缸的正常运转是保证液压系统高性能运行的重要前提，必须要给予保障，因此对液压缸的日常检测与维修显得尤为重要。

大量工业现场数据表明，液压缸在工作时总会受到一些扰动的影响，导致力平衡状态受到破坏，产生不同幅度的颤振，严重时甚至会造成设备损坏和工厂停产。对液压缸进行故障诊断和寿命预测是避免严重后果的手段之一，因此很多专家对该领域进行了大量的研究。马怀祥教授团队主要研究盾构机和挖掘机两种典型工程机械液压系统的工作状态，以压力、流量、振动、温度和油液信号为检测量，应用LabVIEW软件开发工程机械液压系统故障诊断与健康评估系统[3-6]。姜万录教授团队通过实时采集测量数据，利用机器学习算法对电液伺服系统和液压泵等模型的未知参数进行辨识，从而分析非线性动力学行为，进而对其状态监测、PID控制以及寿命预测[7-10]。张健成教授团队在已有的实验平台上对液压泵、液压马达等液压元件性能测试，并在此基础上讨论液压元件功能失效的方式、故障定位所需的信号以及传感器位置安装问题[11-12]。侯保林教授团队针对火炮自动传输弹系统进行深入的故障因素分析，根据弹药协调器的数学模型和特点进行故障因素的参数辨识，并利用虚拟样机模型进行仿真验证理论的真实性[13-14]。

现阶段，针对液压缸故障诊断与寿命预测的研究已经十分深入，但实际应用中存在很多困难，如实际工业中故障状态下的信号很难收集、当检测到故障时故障已经发生、寿命预测需要全生命周期数据等等。因此，对液压系统的日常监测和维护，即时刻关注液压缸的工作状态劣化问题应该被重点考虑。液压缸的劣化程度主要通过活塞杆对两腔的密封性体现。随着液压缸使用次数增加，液压密封件可能会出现化学性损坏或者热降解问题，导致液压缸腔内的密封性变差、油液泄漏、活塞杆与腔内表面摩擦力改变，从而致使液压系统工作状态不佳、效率低，甚至出现故障、停止工作等问题。国内外的众多文献中已指出，摩擦力是影响液压缸工作效率及能量转化的关键因素， 又是影响密封件寿命及液压缸工作可靠性的决定因素之一[15-18]。所以，考虑引入摩擦模型，通过模型的参数变化表征液压缸的劣化趋势。

建立摩擦模型的主要目的是完整体现受力物体的摩擦状态，便于对物体的摩擦力及运动状态精准分析。摩擦模型可以根据物体的运动状态分为静摩擦模型和动摩擦模型。不过，实际工程作业中的物体运动状态具有复杂性、多变性，因此需要选择适合的摩擦力模型刻画复杂情况下的摩擦变化。目前常用的摩擦模型包括库伦模型[19]、库伦+黏性摩擦模型[20]、Stribeck摩擦模型[21]、Karnopp模型[22]以及LuGre模型[23]等。其中，Stribeck摩擦模型的使用率高，应用范围十分广泛。1902年，德国学者Stribeck通过实验证明运动速度、法向载荷和润滑剂的黏度等参数与摩擦系数之间的关系，从而绘制出Stribeck曲线，进而划分边界润滑、混合润滑、流体润滑区域[24]。Stribeck摩擦模型与库伦模型、库伦+黏性摩擦模型相比，具有精度高的优势；与LuGre模型相比，更易于参数辨识、计算量也更小。因此，本研究优先考虑使用Stribeck摩擦模型刻画液压缸受摩擦力情况。

目前，大多数研究都是从如何影响系统稳定性能的角度去分析Stribeck摩擦模型。研究了基于永磁同步电机低速运行时黏滑现象下的控制器设计问题，利用Stribeck摩擦模型对非线性摩擦力矩建模，通过设计补偿控制器解决了系统稳态误差和低速爬行问题[25]。对含有非线性摩擦和间隙的混合系统建模，并利用线性化手段处理Stribeck摩擦模型，应用LQ控制器保证了系统的渐近稳定性[26]。针对具有Stribeck效应的未知不连续摩擦信号的观测或跟踪问题，设计了一种线性扩张状态观测器算法，同时提出了一种线性控制律来动态补偿摩擦扰动并与传统PID控制进行了比较[27]。为了真实地模拟摩擦对交流伺服系统的影响，建立了包含实测Stribeck摩擦干扰因子的工业交流伺服电机三回路非线性模型，采用传统PID和模糊PID对位置环的控制性能进行了仿真研究[28]。然而利用Stribeck摩擦模型研究液压缸劣化问题的文献鲜有，需要进一步探索与发现。

本研究通过最小二乘(Least Squares，LS)算法对不同时刻的Stribeck摩擦模型的参数进行估计，并与初始状态下的Stribeck模型参数进行比较，进而计算液压缸的劣化程度。当Stribeck模型参数发生变化时，说明液压缸动力学模型的参数发生变化，也就是说液压密封件存在劣化现象。与故障诊断、寿命预测不同的是，劣化趋势的刻画是实时的、持续的，需要利用辨识算法不定期对液压缸进行Stribeck模型参数估计。

1 模型建立

根据非线性振动理论和非线性动力学原理，探究液压系统(正常工作)在多重因素影响下的运动特性，利用液压缸活塞位移信号，建立动力学方程并转换成LS格式，为Stribeck参数估计奠定基础。

1.1 机理分析

液压缸正常作业时主要受到惯性力、黏性力、非线性液压弹簧力、非线性摩擦力和外负载力，根据牛顿第二定律，可得系统的力平衡方程[29]：

(1)

式中，m—— 活塞及负载的折合质量

x—— 活塞位移

t—— 运行时间

Fc—— 黏性力

Fk—— 非线性液压弹性力

Ff—— 非线性摩擦力

FL—— 作用在活塞上的任意外负载力

p1，p2，A1，A2—— 无/有杆腔压力和有效面积

本研究以双作用单活塞杆液压缸为研究对象，考虑在液压泵和外负载的作用下，活塞利用液压弹性力克服非线性动态摩擦力做简谐往复运动[30]。根据非线性动力学原理，建立液压缸动力学方程：

(2)

式中，c—— 黏性阻尼系数

K—— 系统的等效刚度，K=Kh+KL

其中，Kh为液压弹簧刚度，是关于位移x的非线性函数，随活塞运动呈现非线性时域变化；KL为负载质量等效弹簧刚度。由于KL≫Kh[31]，所以K的变化不明显，可近似看成一个系统参数。Fd为动摩擦力，可通过Stribeck摩擦模型描述其特性：

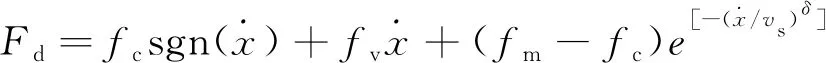
(3)

式中，fc—— 库仑摩擦参数

fm—— 最大静摩擦力

fv—— 黏性摩擦系数

vs，δ—— 经验常数

sgn(x) —— 符号函数，即：

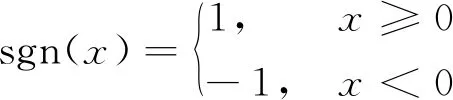
(4)

由于式(3)为非线性模型，文献[32]将Stribeck摩擦模型进行参数线性化得到式(5)，线性化前后如图1和图2所示：

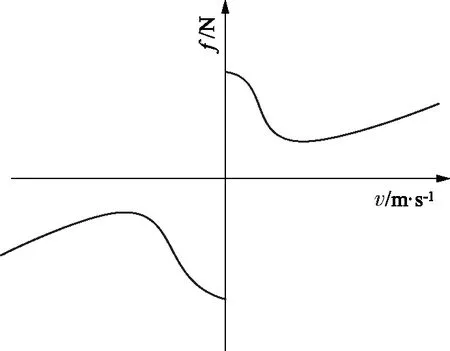
图1 Stribeck摩擦模型

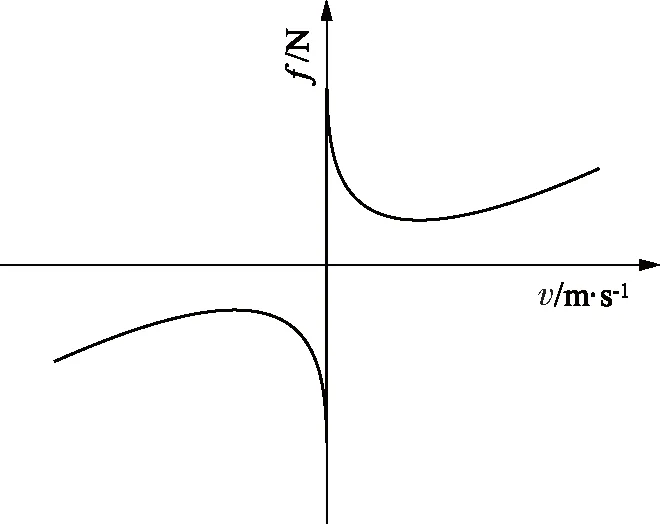
图2 参数线性化Stribeck模型

(5)

其中，fs为Stribeck摩擦参数，参数fc，fv和fs刻画了活塞速度和摩擦力的关系，反应了液压系统的健康程度，因此可以用其变化来刻画液压缸的劣化趋势。

将式(5)代入式(2)，可得：

=p1A1-p2A2-FL

(6)

进一步整理，有：

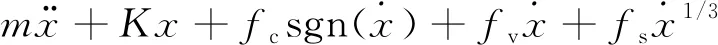
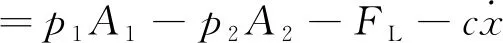
(7)

1.2 LS基本格式

液压缸运动模型式(7)中，工况不同会导致系统参数变化。因此，需要利用实时采集的数据对系统参数进行估计。为此，写出式(7)的LS格式：

系统可测到的量为p1，p2和x，且阻尼系数c一般是已知的[33]，设：

(8)

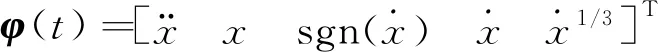
(9)

(10)

则式(7)等价于y(t)=φT(t)θ+d(t)。考虑到测量噪声，则式(7)的LS格式为：

y(t)=φT(t)θ+d(t)

(11)

其中，d(t)为测量噪声，假设服从零均值的高斯分布。在式(11)中，m，K，fc，fv和fs是需要估计的参数；活塞位移、无杆腔和有杆腔的压力、外部轧制力、黏性力组成系统输出；活塞位移x及其一阶导数(速度)和二阶导数(加速度)经符号函数等组成回归向量。

实际系统的控制和测量都是离散的，通常每隔一定时间采集数据，导致位移信号离散化，将式(11)离散化得到：

(12)

其中，k表示采样时刻。

2 基于活塞杆位移信号的Stribeck参数估计

基于式(12)，首先对实时采集的信息处理，得到LS输入输出数据。然后通过LS算法估计模型未知参数，尤其是Stribeck参数。

2.1 LS输入输出数据的求取

液压系统通常使用磁致伸缩直线位移传感器测量位移信号，该传感器鲁棒性较强，可以适用极其恶劣的工业环境，同时测量得到的数据具有高精度、高分辨率等特点。因此，由磁致伸缩直线位移传感器测得的数据可直接采用差分算法求解速度信号vk和加速度信号ak：

(13)

(14)

其中，Δ为差分间隔。差分是微分的一种近似，其主要思想是通过有限差分来近似导数，把求解微分方程的问题转换成求解代数方程的问题。结果的准确性取决于Δ的选取，Δ越小差分效果越好。

另一方面，针对构成LS输出的4个组成部分，逐步进行分析：

(1) 根据公式F=pA可知，p1A1和p2A2分别代表无杆腔和有杆腔的压力。两腔的压力随着活塞位移变化而变化，可通过压力传感器测量；

(2) 外部轧制力FL可根据工况的不同自行设计；

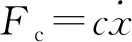
综上，LS算法所需的输入输出数据均已知，接下来利用实时数据估计模型参数。

2.2 根据LS算法估计Stribeck参数

LS辨识算法具有收敛速度快、鲁棒性强等特点，已经成为实验数据参数辨识的主要手段，同时也在工业领域得到了广泛应用。基于式(12)，对系统式(7)的参数进行估计，得到第k时刻模型的参数辨识结果：

(15)

(16)

(17)

Kk，Pk—— 增益矩阵

LS辨识算法的具体实现步骤如算法1所示。

根据算法1可知，给定递推初值，首先采集数据，然后求取LS的输入输出数据，进而根据上一步估计和当前数据更新参数估计值，直至收敛到满足的结果。

3 劣化指标建立

结合实际使用情况，液压缸随着使用时间的增加，部件会产生磨损、老化，其中磨损情况主要体现在活塞杆劣化程度。当活塞杆与密封件的接触表面逐渐存在间隙，摩擦力及运动状态会发生变化。因此，系统模型式(12)的参数是慢时变的，尤其是Stribeck参数。另一方面，劣化是一个长期的变化过程，每隔一段时间对其进行监测就可反应其变化情况。为此，本研究提出双时间尺度劣化趋势评价算法：

(1) 算法1 基于位移信号的Stribeck参数LS估计：

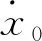
循环：k=1,2,…

输入：第k时刻位移信号xk

根据式(8)和式(9)构建向量yk和φk；

根据式(15)更新Kk；

根据式(17)更新Pk；

返回输入，估计下一时刻模型参数；

结束。

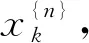
图3 双时间尺度劣化趋势评价算法示意图

(18)

其中，ε为停止条件参数，一般接近于0。第n次估计结束后，设定的时间间隔记作Tn。

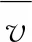
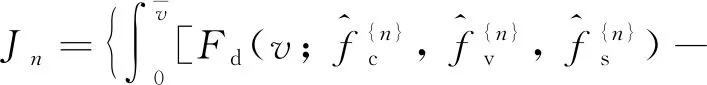
(19)

(2) 算法2 液压缸双时间尺度劣化趋势评价算法：

给定参数估计停止条件阈值ε

循环：n=1,2,…

输出：劣化指标Jn

根据式(19)计算劣化指标Jn；

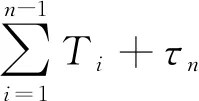
设定间隔时间Tn；

经过时间Tn后，返回输入，上一次的参数估计作为本次估计的初值；

结束。

根据上述算法流程可知，通过计算每次Stribeck参数与初始Stribeck参数的差值，刻画液压缸工作状态劣化曲线。现场人员通过对劣化曲线的分析，确定液压缸目前的劣化程度，为是否更换系统部件提供依据。

算法2之所以称为是双时间尺度的，是因为每次参数估计的数据采集时间跨度是一个时间尺度，间隔时间构成另一个时间尺度。每次参数估计考虑的实时数据个数可能存在差异，导致数据采集的时间跨度不同，同时每次的时间间隔遵循液压缸实时工作状态进行设定，也存在差异。

4 数值仿真与实例验证

4.1 数值仿真

在同一工况下，针对液压缸动力学模型式(2)，利用MATLAB软件编写仿真程序，探究液压缸不同时间段的劣化程度。

第一步，建立式(7)的仿真模型，选取6个时间段，每个时间段给定不同的Stribeck模型参数并进行劣化趋势分析。仿真参数取值如下：

1) 固定参数

m=350，K=30，c=2，FL=5，p1A1-p2A2=20+2sin(2k)，k为采样时刻。

2) 变化参数

6个时间段给定不同Stribeck参数，便于刻画液压缸劣化趋势，具体取值如表1所示。

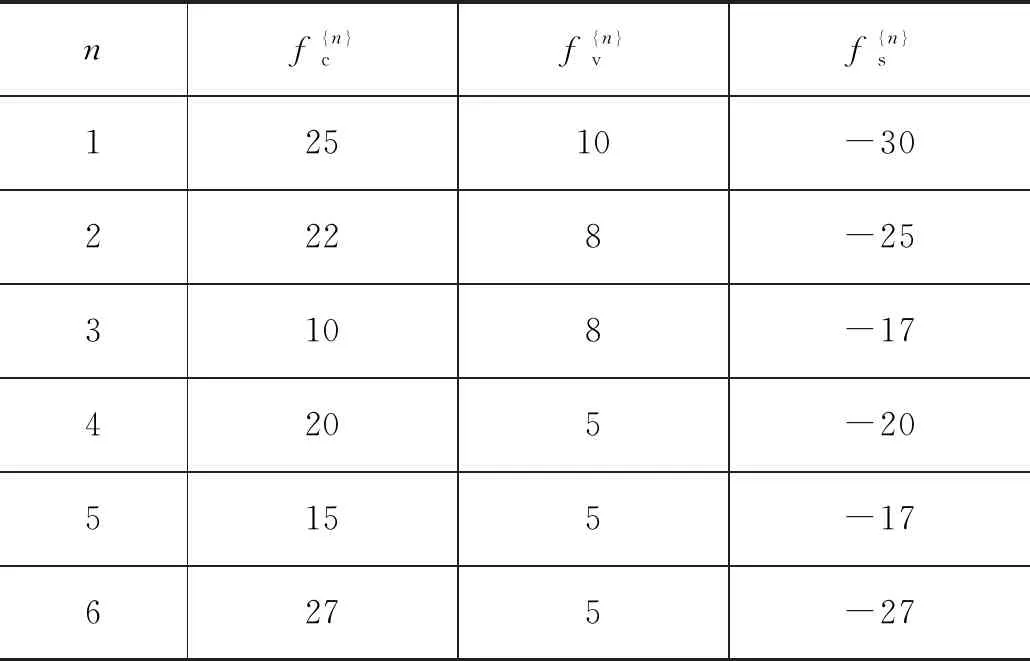
表1 变化参数

第二步，根据给定参数，利用四阶Runge-Kutta算法构造6个不同时间段的位移信号，初值[x0,v0]=[0,4]，采样间隔h=0.01，每个时间段内数据为10000个。基于差分算法式(13)、式(14)求解速度、加速度数据，结果如图4～图9所示。

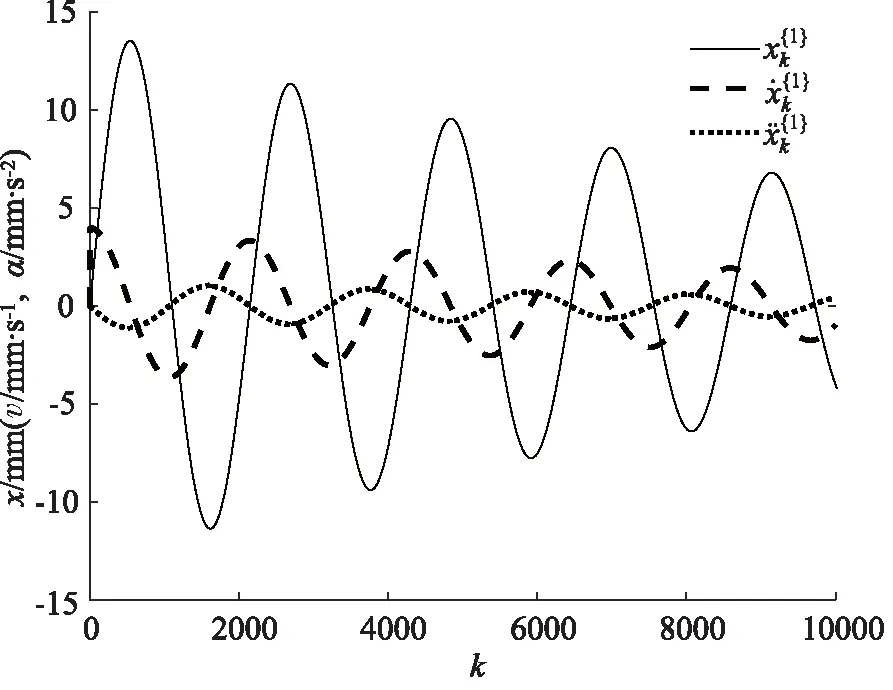
图4 第一组数据

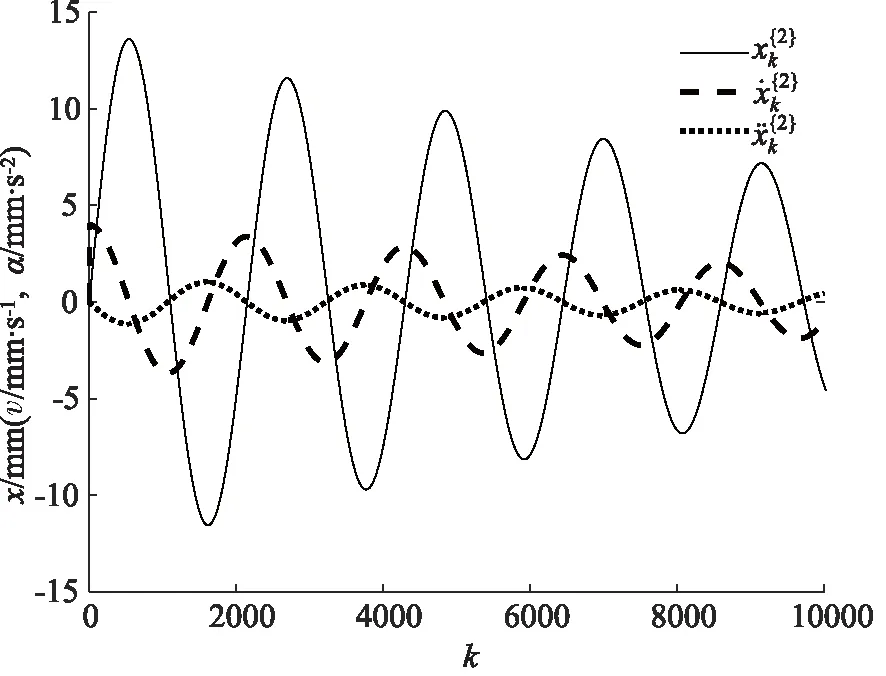
图5 第二组数据

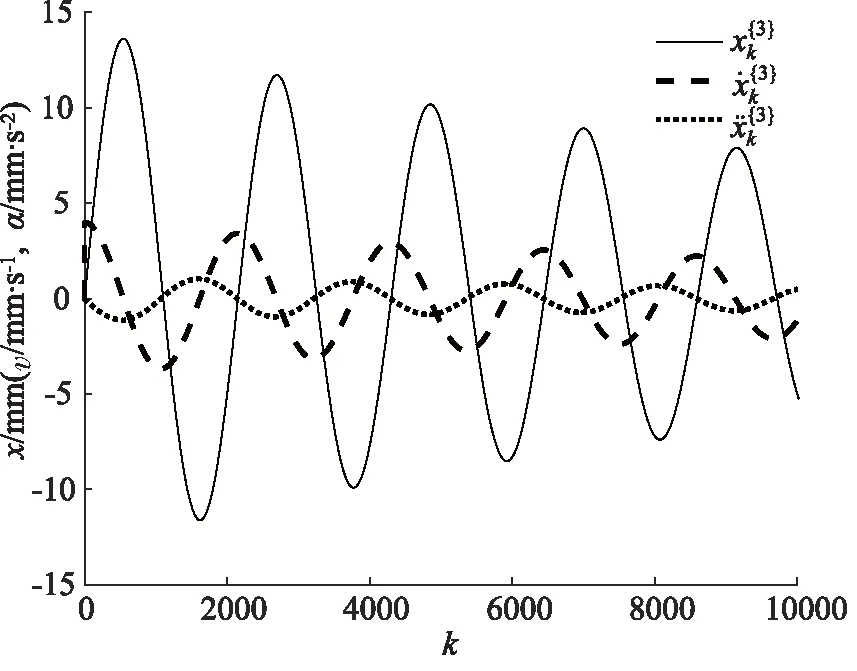
图6 第三组数据

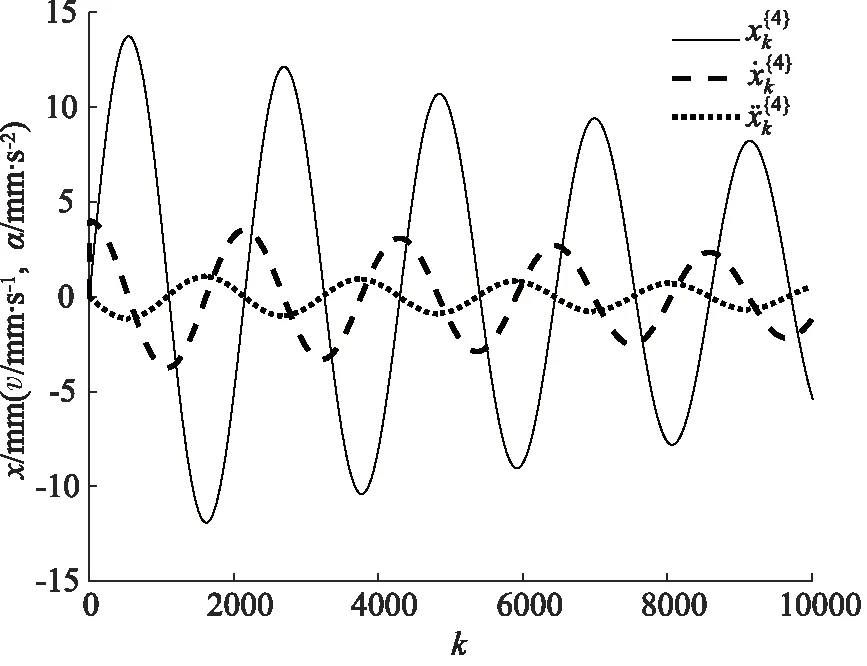
图7 第四组数据

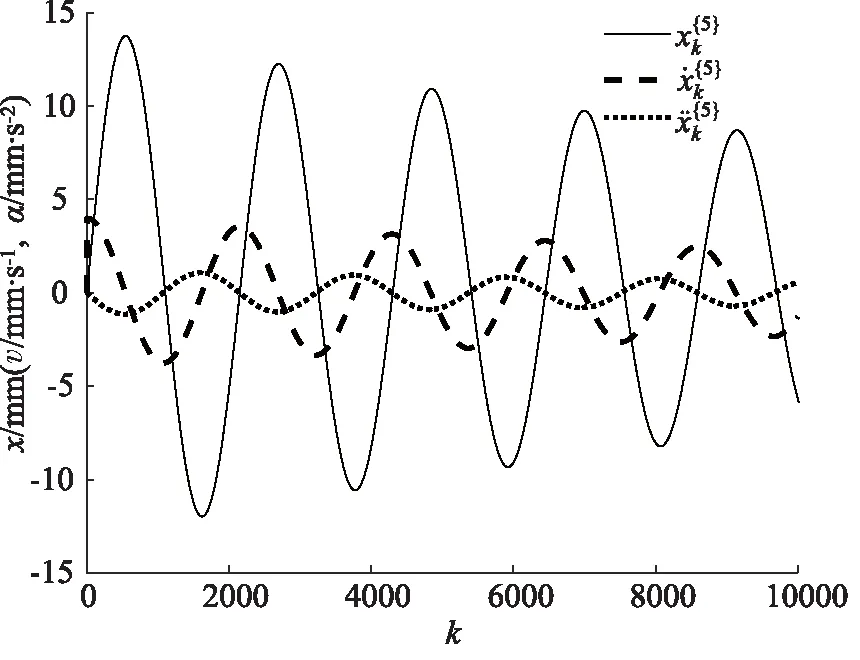
图8 第五组数据

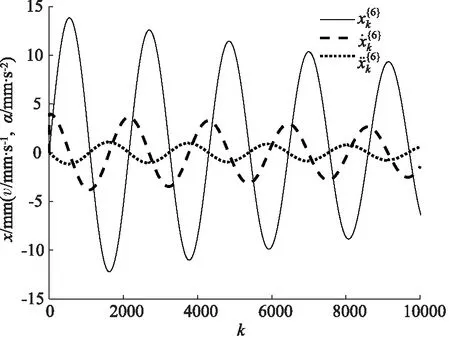
图9 第六组数据

从上图可以看出，6个时间段内的液压系统位移信号均呈周期性变化，表明活塞杆在液压缸中做简谐运动。位移信号为正数时表示活塞杆向无杆腔方向运动，有杆腔面积扩大、无杆腔面积缩小，位移信号为负数时情况相反。此外，由于劣化不具有故障的突发性，位移信号在不同时间段变化的并不明显。

第三步，设定ε=1×10-6，测量噪声d(t)服从均值为0、方差1的高斯分布，将构造的输入输出数据带入算法1，分别估计6个时间段的Stribeck模型参数，如图10～图15所示，并且基于被估Stribeck模型参数刻画6组Stribeck模型曲线，如图16所示。

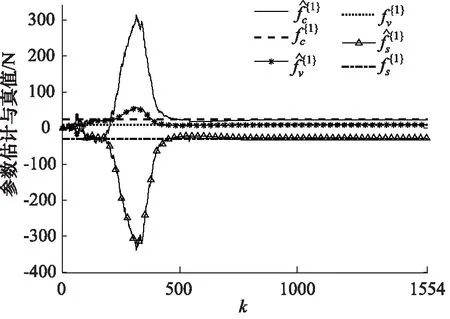
图10 第一组Stribeck参数估计

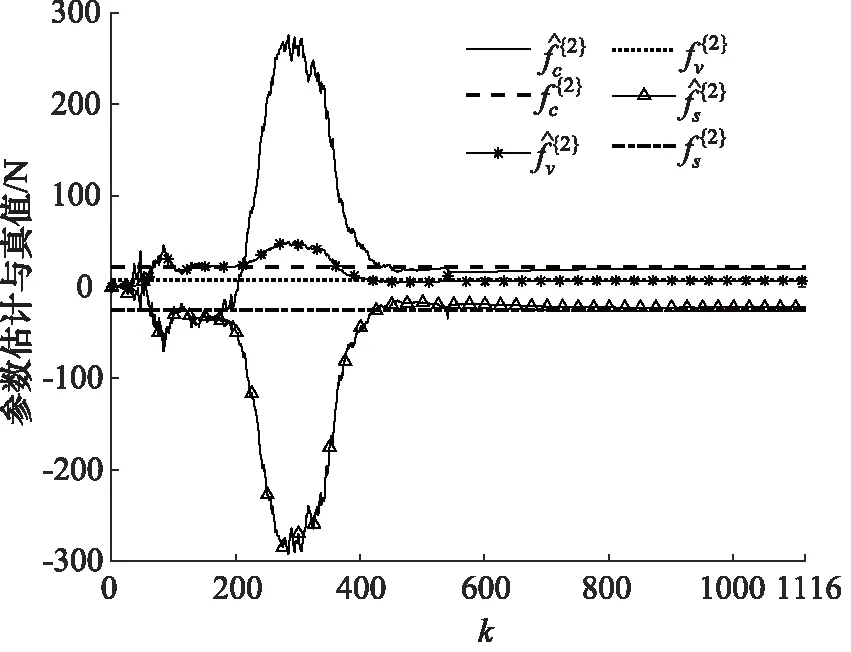
图11 第二组Stribeck参数估计

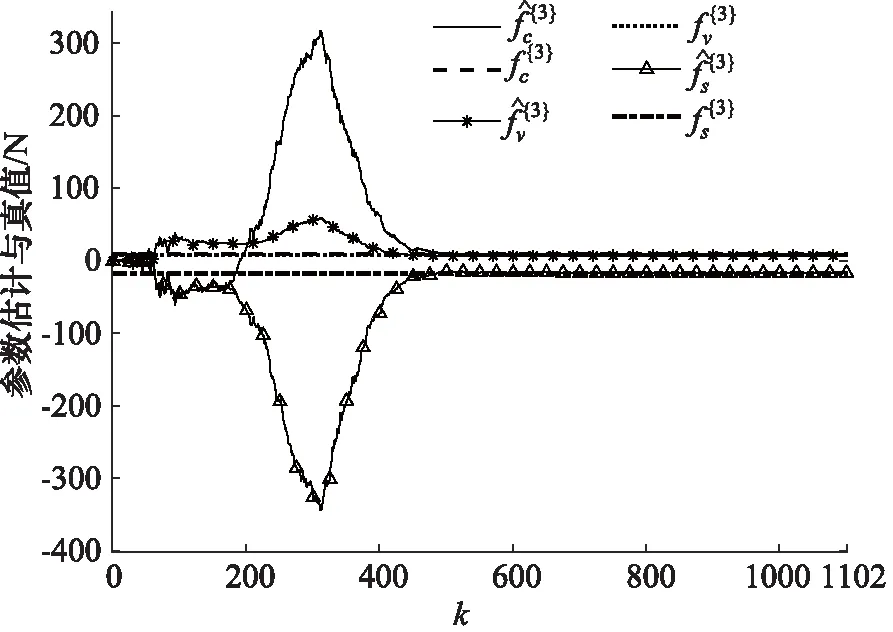
图12 第三组Stribeck参数估计

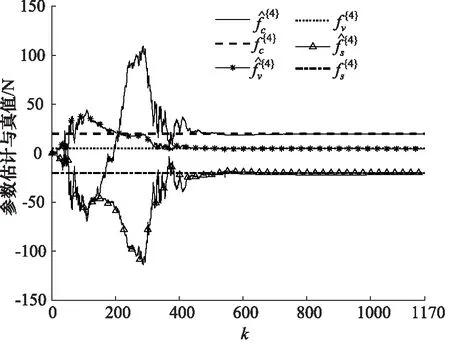
图13 第四组Stribeck参数估计

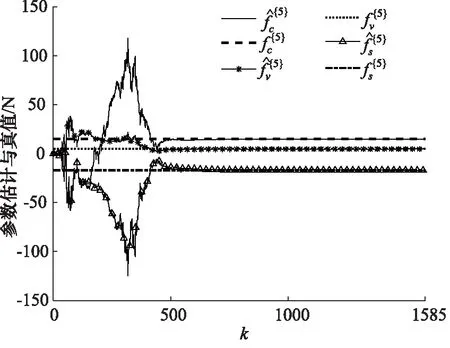
图14 第五组Stribeck参数估计

从图10～图15中可以看出每组估计参数所用的数据量都不同，Stribeck参数最终都会收敛到真值附近，而且算法的收敛速度较高、抗干扰能力较强。同时可以发现参数fv的估计精确度相比其他2个Stribeck参数要高，其原因是在液压缸动力学方程中关于fv的项是线性的，关于另外2个参数的项是非线性的。通过图16可以知道液压缸状态劣化导致Stribeck模型曲线发生变化，但是曲线走势类似。

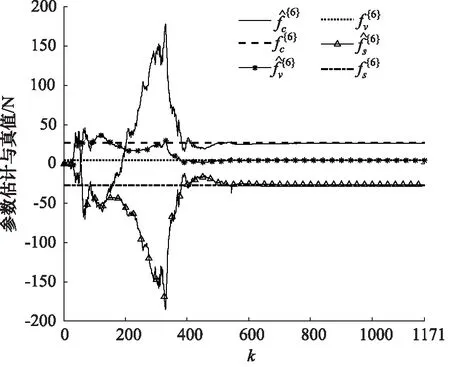
图15 第六组Stribeck参数估计

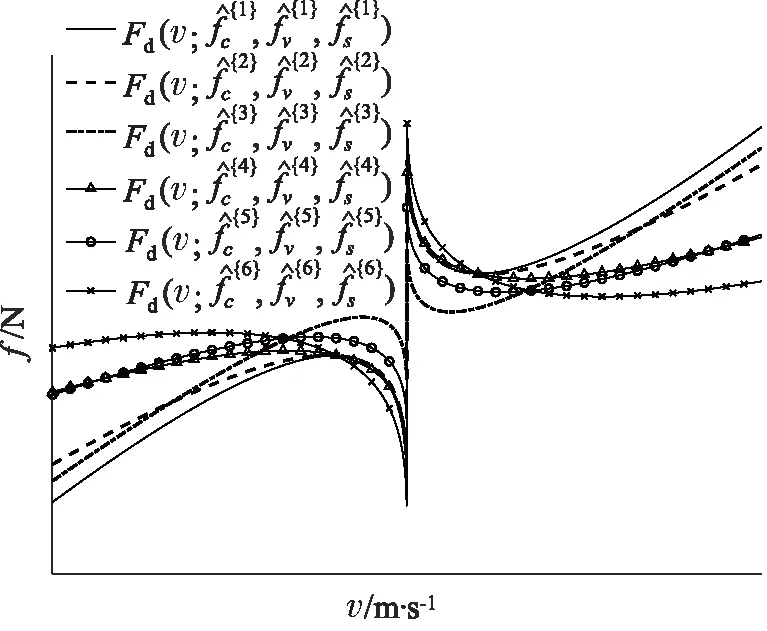
图16 不同时间段下Stribeck模型曲线

影响Stribeck模型的有3个参数分别是fc，fv和fs，根据给定的变化参数和图17可知，3个参数的变化并不能直接评价液压缸劣化趋势，而是利用不同时间段下的3个参数刻画Stribeck曲线，通过对比曲线的变化来判断劣化趋势。

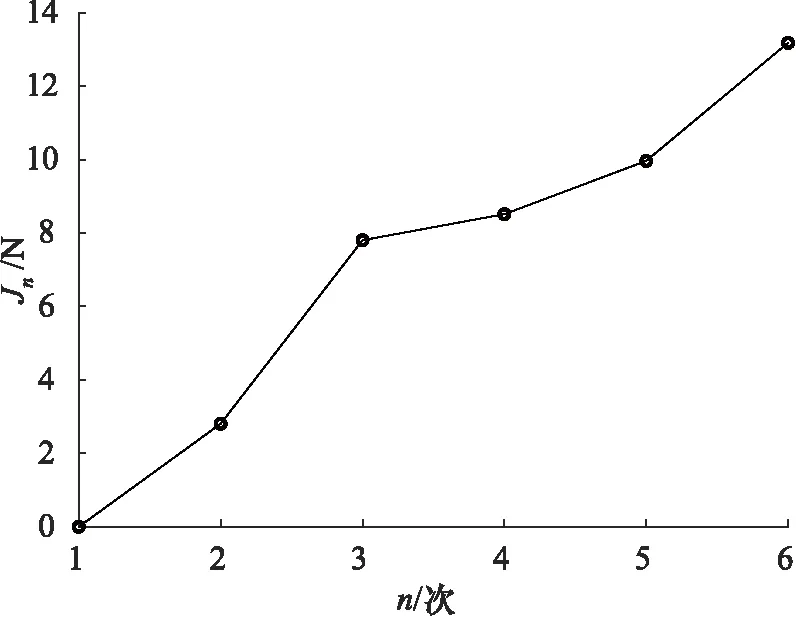
图17 劣化趋势

4.2 工业实例

采用某炼钢厂提供的某AGC液压缸作为实验对象，液压系统部分实物如图18所示。以3个月为周期，利用IBA数据采集系统采集5组液压缸位移x信号、无/有杆腔压力p1,p2信号以及轧制力FL信号，具体数据如图19～图23所示。

图18 AGC液压缸实物图

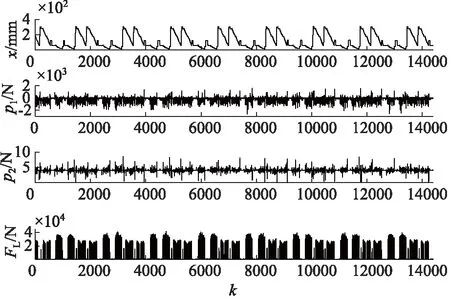
图19 第一组信号

由图19～图23可以看出，4种测量信号呈周期性变化，且5组数据的曲线走势大致相同，这表明液压缸一直处于正常工作状态。

利用算法1辨识Stribeck参数，结果如图24～图28所示，可以看出算法均收敛。最终估计值如表2所示，并给出Stribeck模型曲线，如图29所示。

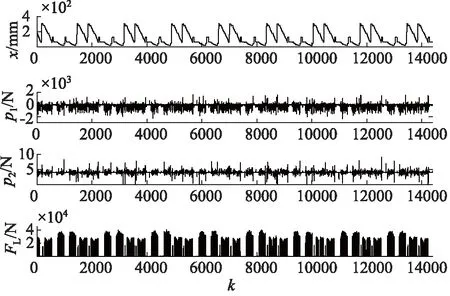
图20 第二组信号

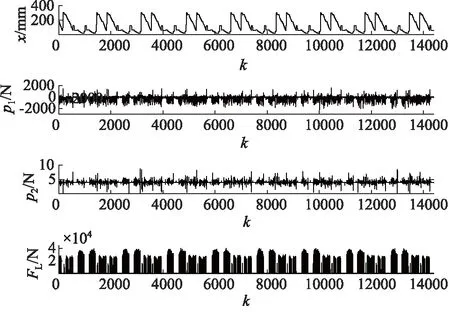
图21 第三组信号

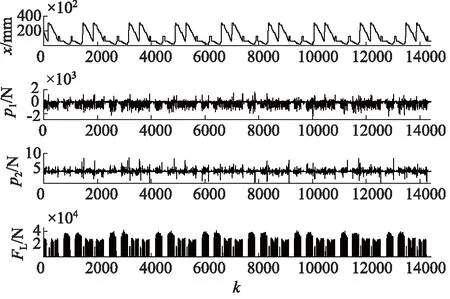
图22 第四组信号

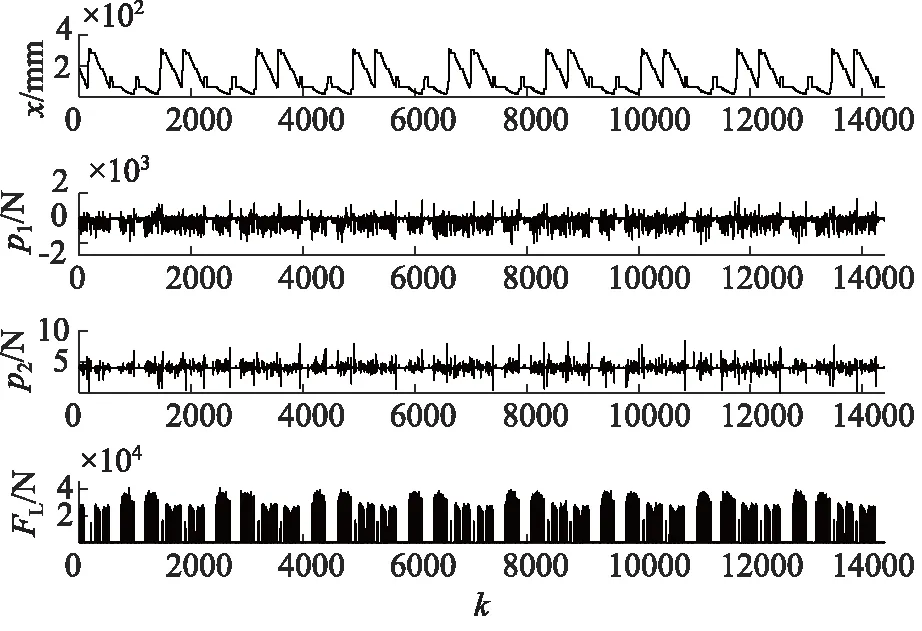
图23 第五组信号

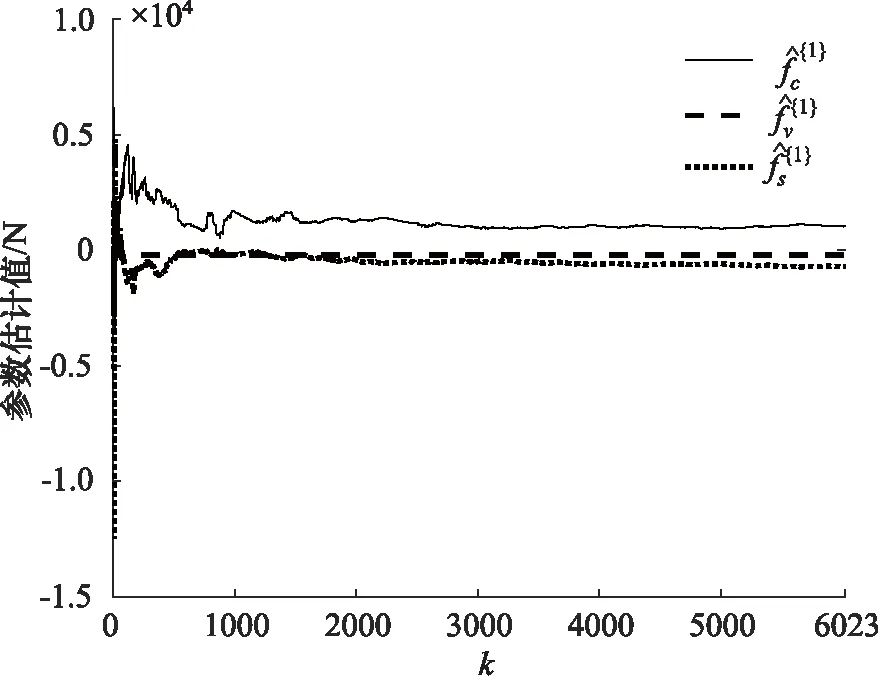
图24 第一组Stribeck参数估计

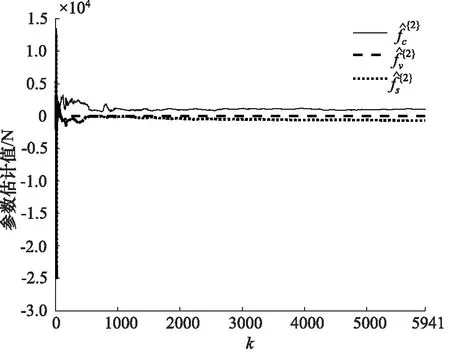
图25 第二组Stribeck参数估计

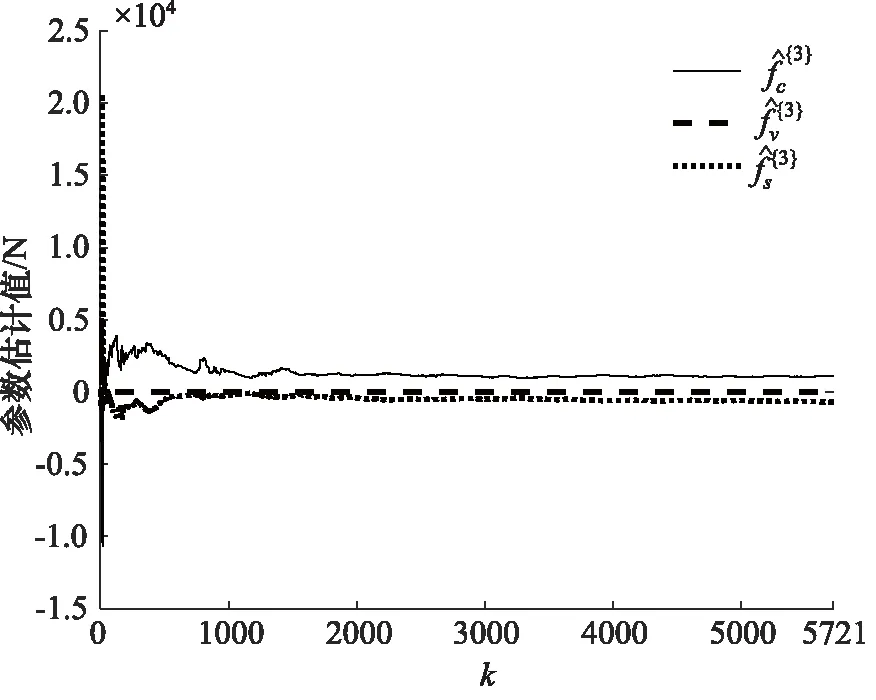
图26 第三组Stribeck参数估计

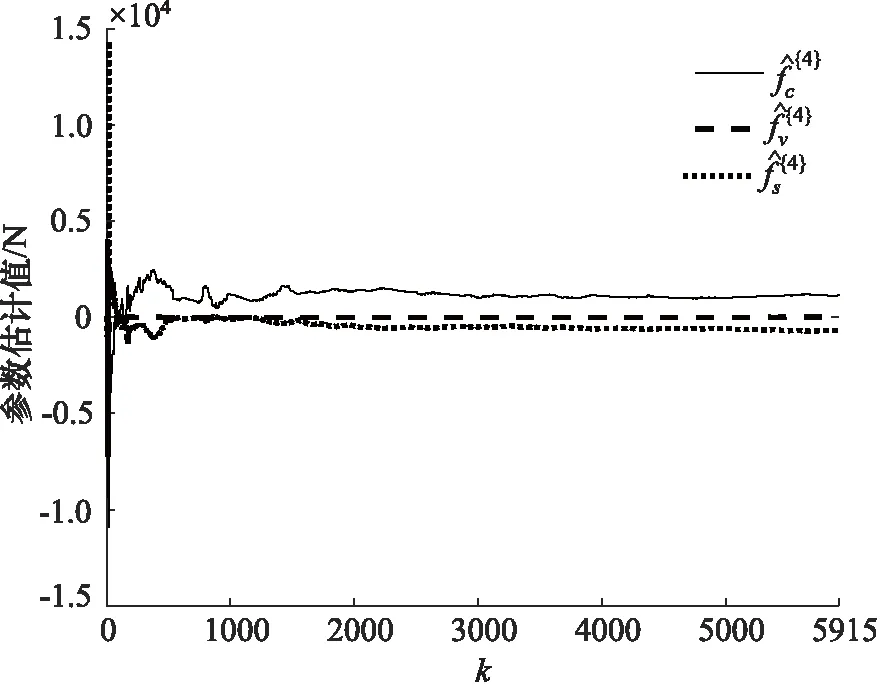
图27 第四组Stribeck参数估计

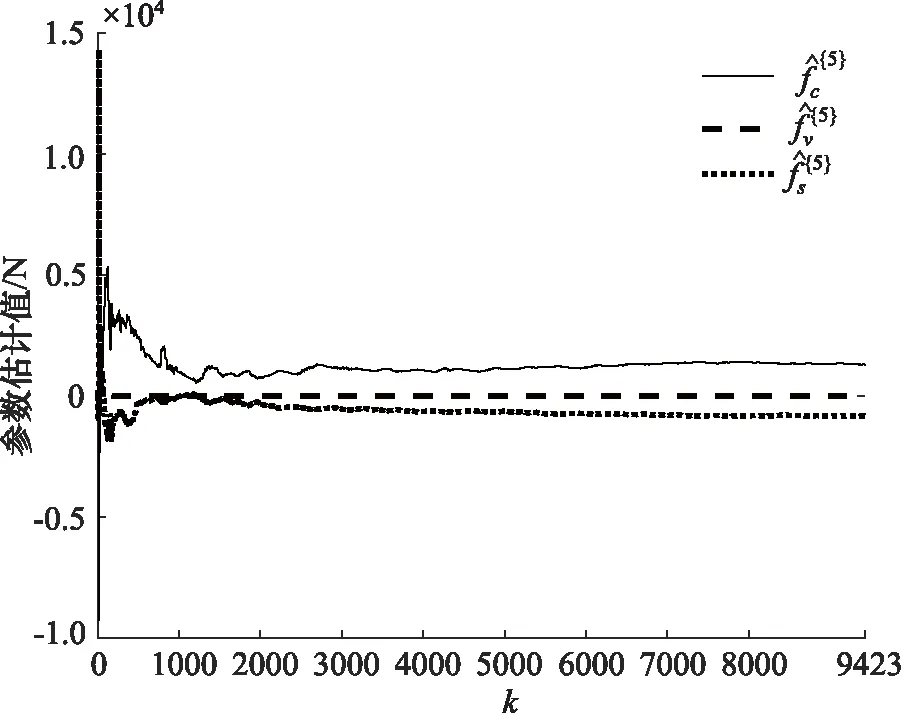
图28 第五组Stribeck参数估计

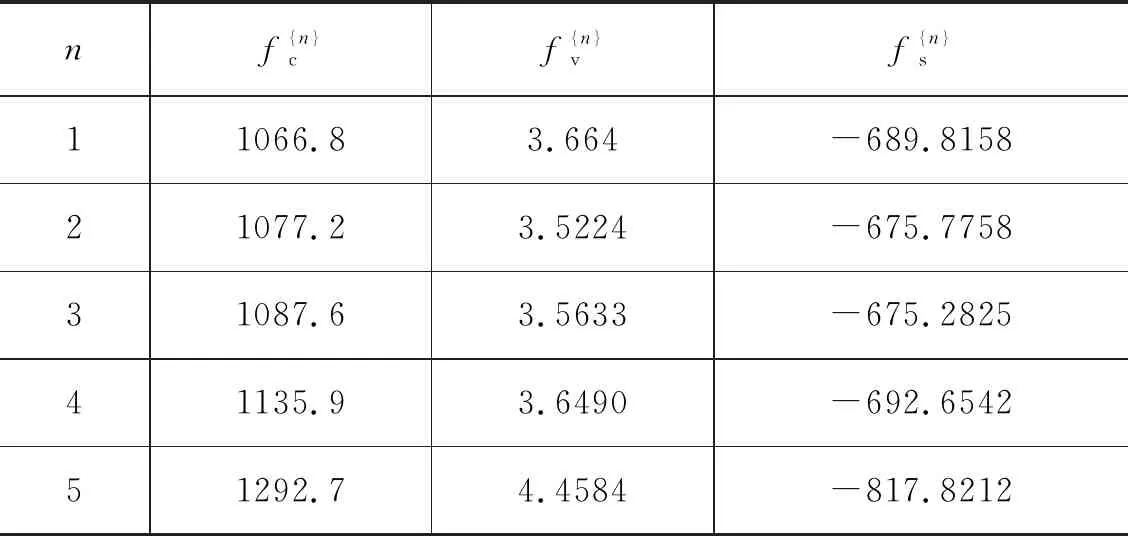
表2 Stribeck参数辨识结果

图29 不同时间段下Stribeck模型曲线

根据算法2绘制Jn的变化曲线，结果如图29所示，可以看出Jn随n增大而增大，Stribeck模型曲线逐渐偏离初始状态，这就给出了液压缸的劣化趋势。

5 结论

本研究主要研究基于Stribeck曲线评价液压缸劣化趋势问题。首先，通过对液压系统工作方式的分析，找到内部结构受力变化规律，从而建立液压缸动力学方程；其次，线性化摩擦力Stribeck模型，建立LS参数辨识基本格式；然后，通过传感器采集数据、对数据差分，结合先验信息确定LS输入输出数据；进而，自主选择双尺度时间段，在估计Stribeck参数的基础上计算液压缸劣化指标；最后，通过6组仿真数据验证提出的劣化算法的正确性和有效性。未来可以探索更多形式的劣化趋势评价指标，建立质量相关的评价方法。

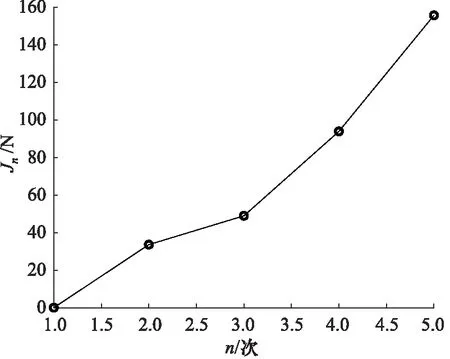
图30 劣化趋势