基于能量增强的双斜式轴向柱塞泵滑靴磨损故障诊断方法

乔世昌， 许顺海， 王少萍， 石 健， 李振坤， 刘小平， 王伟杰， 白林迎

(1.北京航空航天大学 自动化科学与电气工程学院， 北京 100191； 2.中铁工程装备集团有限公司， 河南 郑州 450016)

引言

液压泵是液压系统中十分关键的部件，拥有功重比高等很多优势，对于液压系统中其余元件的健康运行有至关重要的影响[1]。双斜式轴向柱塞泵是液压泵的一种，广泛应用于盾构机等大型设备中，常常面临高压、重载、强振动等恶劣工况，因此对双斜式轴向柱塞泵的故障诊断是十分必要的[2]。

配流副、柱塞副以及滑靴副是双斜式轴向柱塞泵之中主要的摩擦副，摩擦副的磨损会引起双斜式轴向柱塞泵发生滑靴磨损、配油盘磨损等故障[3]。其中，滑靴副主要负责双斜式轴向柱塞泵的传力，滑靴副的磨损问题在工程实践中是十分容易发生的，特别是对于盾构机中的双斜式轴向柱塞泵来说，剧烈的冲击载荷和油液中混入杂质都可能加剧滑靴副的磨损程度，磨损过于严重时可能产生松靴故障，使轴向柱塞泵失去平稳安全的运行状态[4-5]。

准确诊断出双斜式轴向柱塞泵的滑靴磨损故障是保证其平稳、安全运行的关键。但由于其结构复杂，滑靴磨损故障特征信号弱，且环境噪声大，故障特征易被淹没，诊断难度大。因此如何实现对双斜式柱塞泵滑靴磨损故障的精准诊断具有工程意义。在发生松靴故障时，双斜式轴向柱塞泵的振动信号会发生一定变化[6]。双斜式轴向柱塞泵发生振动时，借助泵壳更容易采集振动信号，因此振动信号分析多为针对泵壳进行[7]。而单纯的振动信号的分析，信号特征不够明显，因此需要进一步的分析。

针对柱塞泵领域，诸多学者都进行过研究：王少萍等[8-9]研究了液压泵的信息融合故障诊断算法；赵群等[10]研究了不确定振动传递路径方面；ERICSON L[11]建立了液压泵两自由度振动模型，得到了液压泵振型和稳态响应，并通过数值模拟得到泵的动态响应；KUMAR等[12]建立了一种新的对称单值中性交叉熵测度，来对轴向柱塞泵轴承的相关故障进行研究；王登铭[13]利用粒子群算法与BP神经网络相结合来分析轴向柱塞泵的部分故障；CASOLI等[14]提出了一种可变排量轴向柱塞泵故障诊断方法，并通过循环平稳性理论对加速度信号进行分析验证；唐宏宾等[15]采用 EMD对柱塞泵振动及压力信号进行特征提取并采用多信息进行故障诊断；孙少武[16]将试验台上柱塞泵不同故障下的振动信号进行时域方法处理，并使用深度学习的方法加以诊断；胡晋伟等[17]采用不同的特征提取方法对柱塞泵常见故障进行诊断并采用极限学习机进行故障识别；曾祥辉等[18]运用核超限学习机方法对轴向柱塞泵的相关故障进行了探究；BENSAAD等[19]使用非线性状态模型对泵的动态比例建模并采用扩展的卡尔曼滤波器估计活塞腔的压力来甄别磨损柱塞。本研究的对象为盾构机中的双斜式轴向柱塞泵，目前国内外对双斜式轴向柱塞泵的振动传递路径研究很少，而对双斜式柱塞泵壳体的轴向和径向振动信号的叠加进行能量增强来进行滑靴磨损故障诊断，相比于传统方法提供了一个新的思维方向。

1 双斜式柱塞泵滑靴磨损的振动动力学模型

1.1 振动动力学建模

建模前进行假设：忽略转子偏心所造成的机械振动；将配流盘与前壳体统一进行受力分析；忽略柱塞存在的摆动；忽略球铰运动；假设双斜式轴向柱塞泵内部各部件间的油膜是刚性弹性体；轴承存在的轴向阻尼也忽略不计；将缸体与传动轴统一进行受力分析。

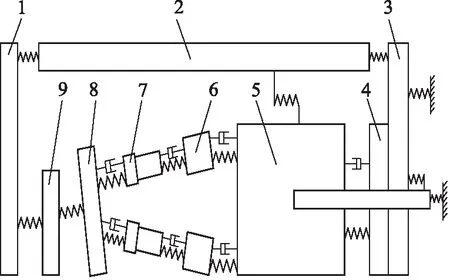
1.后壳体 2.中壳体 3.前壳体 4.配流盘 5.缸体及传动轴 6.油液 7.滑靴 8.斜盘 9.变量机构

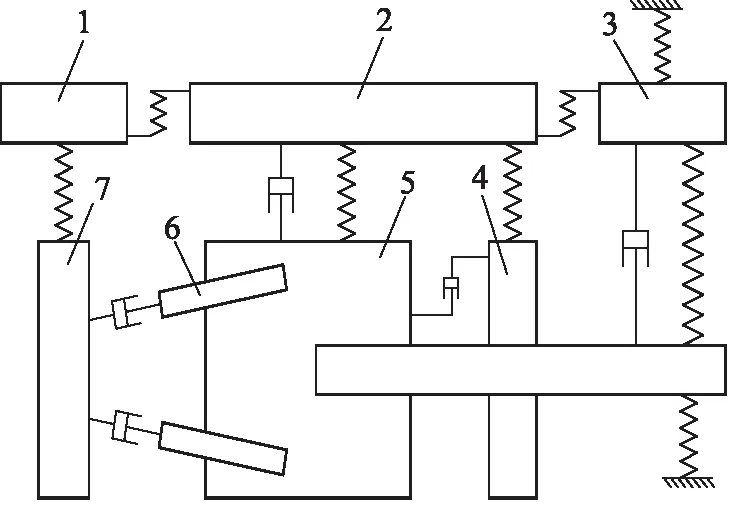
1.后壳体 2.中壳体 3.前壳体 4.配流盘 5.缸体及传动轴 6.柱塞滑靴组件 7.斜盘

建立双斜式柱塞泵松靴故障模型并求解，模型建立和求解过程如下。

首先，建立双斜式柱塞泵后壳体轴向振动微分方程：

(1)

式中，m1—— 双斜式轴向柱塞泵后壳体的质量

x1—— 双斜式轴向柱塞泵后壳体在受力时轴向上的位移

k19—— 后壳体与变量机构处轴向上的刚度

x9—— 变量机构在受力时的轴向上的位移

k12—— 双斜式轴向柱塞泵后、中壳体处轴向上的刚度

x2—— 中壳体在受力时轴向上的位移

然后，建立双斜式柱塞泵中壳体轴向振动微分方程：

(2)

式中，m2—— 双斜式轴向柱塞泵中壳体的质量

kr—— 双斜式轴向柱塞泵滚子轴承的轴向刚度

x5—— 双斜式轴向柱塞泵缸体受力时在轴向上发生的位移

k23—— 中、前壳体处轴向上的刚度

x3—— 双斜式轴向柱塞泵前壳体受力时在轴向上发生的位移

最后,建立双斜式柱塞泵前壳体轴向振动微分方程：

(3)

式中，m3—— 双斜式轴向柱塞泵前壳体质量

kd—— 双斜式轴向柱塞泵深沟球轴承处轴向上的刚度

k3s—— 前壳体与固定端处轴向上的刚度

c4—— 双斜式轴向柱塞泵配流副油膜的阻尼

k4—— 双斜式轴向柱塞泵配流副处油膜的刚度

建立双斜式柱塞泵变量机构轴向振动微分方程：

(4)

式中，m9—— 双斜式轴向柱塞泵变量机构的质量

k89—— 双斜式轴向柱塞泵变量机构与斜盘之间的刚度

γ—— 柱塞倾角

x8—— 斜盘在受力时候的轴向上的位移

建立双斜式柱塞泵斜盘轴向振动微分方程：

k89cosγ(x8-x9)=0

(5)

式中，m8—— 斜盘的质量

n—— 柱塞个数

c7—— 滑靴支承油膜的阻尼

θ—— 斜盘倾角

k7—— 滑靴支承油膜的刚度

建立双斜式柱塞泵柱塞轴向振动微分方程：

(6)

式中，Fz—— 激振力

m7—— 柱塞滑靴的质量

x7—— 受力时柱塞滑靴轴向振动上的位移

xb-z—— 受力时第z个柱塞腔之中油液轴向上的位移

xa-z—— 受力时第z个柱塞腔轴向上的位移

cb-z—— 第z个柱塞腔柱塞副油膜阻尼

kb-z—— 第z个柱塞腔油液的刚度

建立双斜式柱塞泵油液轴向振动微分方程：

(7)

式中，mb—— 双斜式轴向柱塞泵第z个柱塞腔油液的质量

建立双斜式柱塞泵缸体及传动轴轴向振动微分方程：

kr(x2-x5)-kd(x3-x5)+k4(x5-x3)+

(8)

式中，m5—— 缸体及传动轴的质量

k5c—— 缸体和联轴器处轴向上的刚度

建立双斜式柱塞泵缸体及传动轴径向振动微分方程：

kdy(y5-y3)=F

(9)

式中，y5—— 缸体在受力时候径向上的位移

cry—— 柱塞泵滚子轴承的径向阻尼

cdy—— 深沟球轴承的径向阻尼

y3—— 前壳体在受力时候径向上的位移

k5cy—— 传动轴和联轴器处的径向上的刚度

y2—— 中壳体在受力时候径向上的位移

c45y—— 缸体和配流盘处径向上的摩擦阻尼

y4—— 配流盘在受力时候径向上的位移

y7—— 斜盘在受力时候径向上的位移

c67y—— 滑靴与斜盘处径向上的摩擦阻尼

kry—— 滚子轴承处径向刚度

kdy—— 深沟球轴承处径向刚度

建立双斜式柱塞泵配流盘径向振动微分方程：

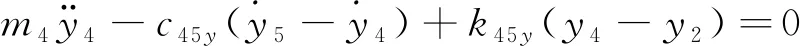
(10)

式中，k45y—— 中壳体和配流盘处接触刚度

建立双斜式柱塞泵前壳体径向振动微分方程：

k23y(y3-y2)=0

(11)

式中，k3sy—— 固定端和前壳体处径向上的刚度

k23y—— 前、中壳体处径向上的刚度

建立双斜式柱塞泵中壳体径向振动微分方程为：

k23y(y3-y2)+k12y(y2-y1)=0

(12)

式中，cry—— 滚子轴承处径向阻尼

k12y—— 中、后壳体之间的径向刚度

y1—— 后壳体在受力时候径向上的位移

建立双斜式柱塞泵后壳体径向振动微分方程为：

(13)

式中，k18y—— 双斜式柱塞泵变量机构的径向刚度

建立双斜式柱塞泵斜盘径向振动微分方程：

(14)

将双斜式柱塞泵轴向振动微分方程和径向振动微分方程分别列写并建立模型，将双斜式柱塞泵参数代入模型，并运用龙格-库塔法求解模型。

1.2 故障状态下仿真模型

双斜式轴向柱塞泵仿真流程图见图3，仿真振动信号是基于双斜式轴向柱塞泵基础参数生成的，包括但不限于双斜式柱塞泵的几何参数与工况参数。具体来说，仿真振动信号由振动物理模型和求解器组成。

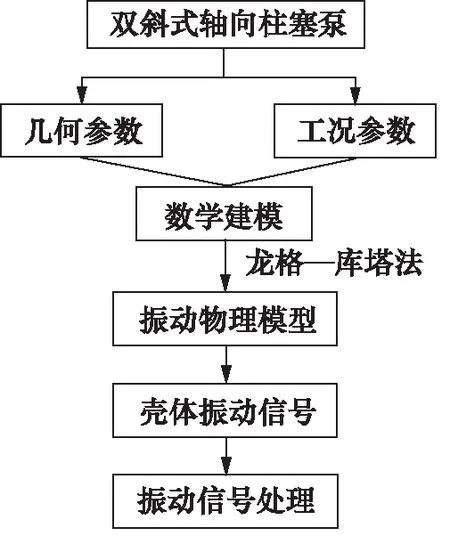
图3 双斜式轴向柱塞泵仿真流程

为了对比故障状态与正常运行下双斜式轴向柱塞泵的相关性能参数的变化情况。本研究使用MATLAB软件进行仿真，首先对双斜式轴向柱塞泵进行数学建模，求解器采用龙格-库塔法求解振动物理模型，振动信号采集单元的输入为双斜式轴向柱塞泵的基础参数和工况参数，输出为壳体的振动信号。

为了验证数学模型的准确性，故进行故障状态下的仿真，在仿真过程中将双斜式轴向柱塞泵转速设置为1500 r/min，并注入滑靴磨损故障，可以仿真得到前壳体的振动加速度的时域及频域曲线。

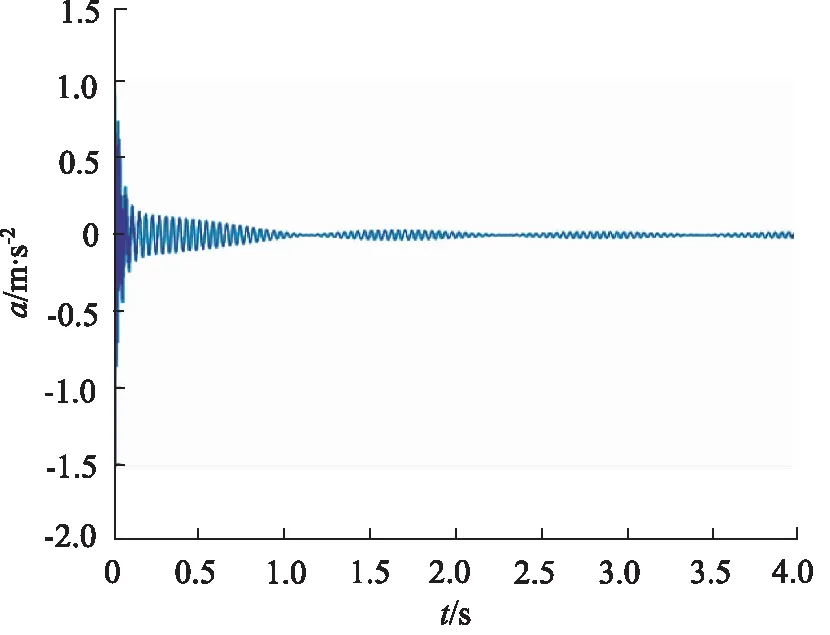
图4 滑靴故障时前壳体仿真时域信号

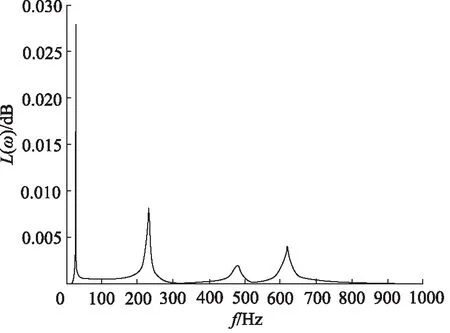
图5 滑靴故障时前壳体仿真频域信号

对滑靴磨损时的前壳体径向振动信号进行小波包能量谱分解，如图6所示。

图6 滑靴故障时径向能量分布信号

根据滑靴故障时双斜式柱塞泵径向能量分布图，可以得知第一频段在发生滑靴故障后变化幅度最大，第五频段在发生滑靴故障后变化幅度最小。

2 基于小波包能量谱的故障诊断方法

2.1 小波能量谱

小波包方法能够将柱塞泵原始信号数据分解到多个频段里，当柱塞泵出现故障的时候，对信号的不同频段能量的影响各有不同。根据能量在不同频段能量的差异性分布来定位故障所在的频段，而小波包分解后各频段能量的分布特点是识别柱塞泵是否故障的重要依据。能量谱中各个频段是相互正交且独立的，并且所有频段之中信号的能量总和保持为定值。

设离散信号xk,m(i)的数据长度为N，其能量可以表示为：

(15)

式中，k为分解次数；m为分解频段的位置序号(m=0,1,…,2k-1)。根据能量守恒定律，可以得到：

(16)

将第m频段信号的能量比上初始总能量，求出相应频段的能量百分比例：

(17)

全部频段能量比例的总和应等于1，即：

(18)

柱塞泵测得的振动信号被小波包划分成各个频段，每个频段的能量可以有效反映柱塞泵在不同频段内的运行状态。因此，用小波能量谱分析柱塞泵故障是可行的。

2.2 能量谱叠加

(19)

轴向振动信号能量占据总能量的百分比记作：

(20)

叠加能量第m频段能量百分比例则为：

(21)

全部频段能量比例的总和应等于1，即：

(22)

3 试验验证

3.1 试验环境与载荷特征

本次试验为750 mL/r双斜式轴向柱塞泵，有高压、大排量和变载荷等特点。测试转速为1500 r/min，整个试验主回路压力设置为35 MPa，试验工况有软土、无水砂卵石、富水砂卵石、岩石和极限5种。采用磁力吸座在泵体的轴向与纵向上安装6个加速度传感器，并使用数据采集箱采集试验过程中的振动信号。

3.2 试验数据小波包能量谱信号分析

本次试验数据取轴向上的4号传感器和径向上的2号传感器的振动信号进行分析，安装示意图如图7所示。加速度传感器型号为FC-AD01-200g，振动信号由数据采集箱采集，采样频率为2050 Hz。

图7 试验现场传感器安装示意图

1) 试验数据小波包能量谱轴向信号分析

滑靴对比示意图见图8，滑靴故障轴向振动时域信号和无故障状态下的轴向振动时域信号对比如图9所示。

图8 正常滑靴(左)和磨损滑靴(右)对比

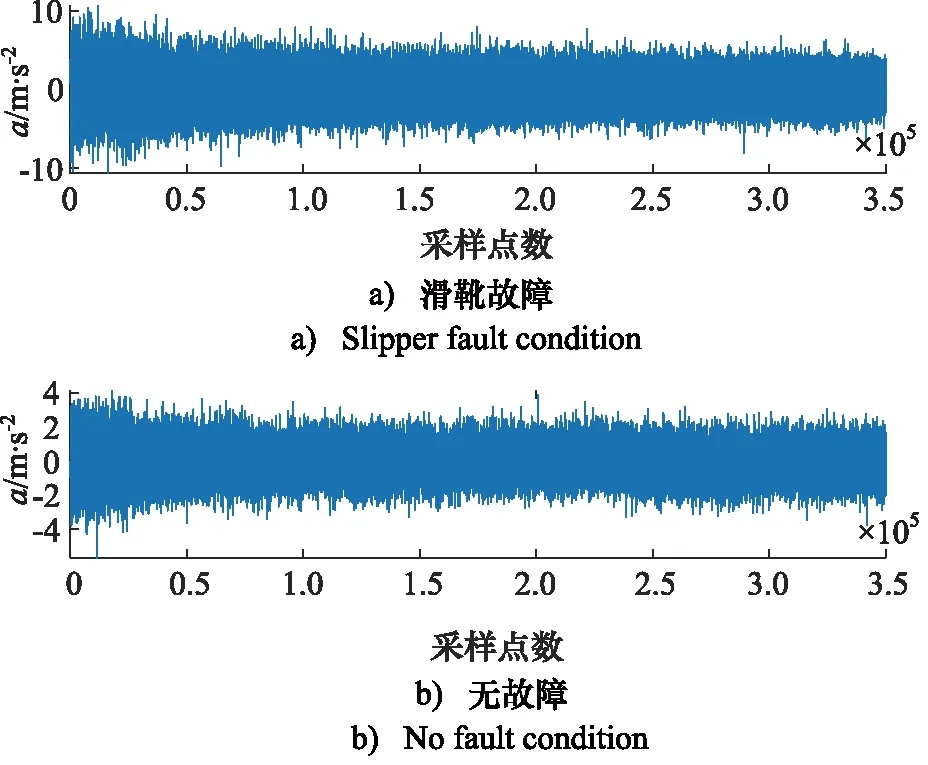
图9 滑靴故障和无故障状态下轴向振动时域信号对比

由图9可以看出，双斜式轴向柱塞泵在发生滑靴故障时，纵坐标加速度的幅值变化范围更大一些，但是只能初步进行判断，接下来对故障信号使用快速傅里叶变换这一传统的特征提取方法进行处理，如图10所示。

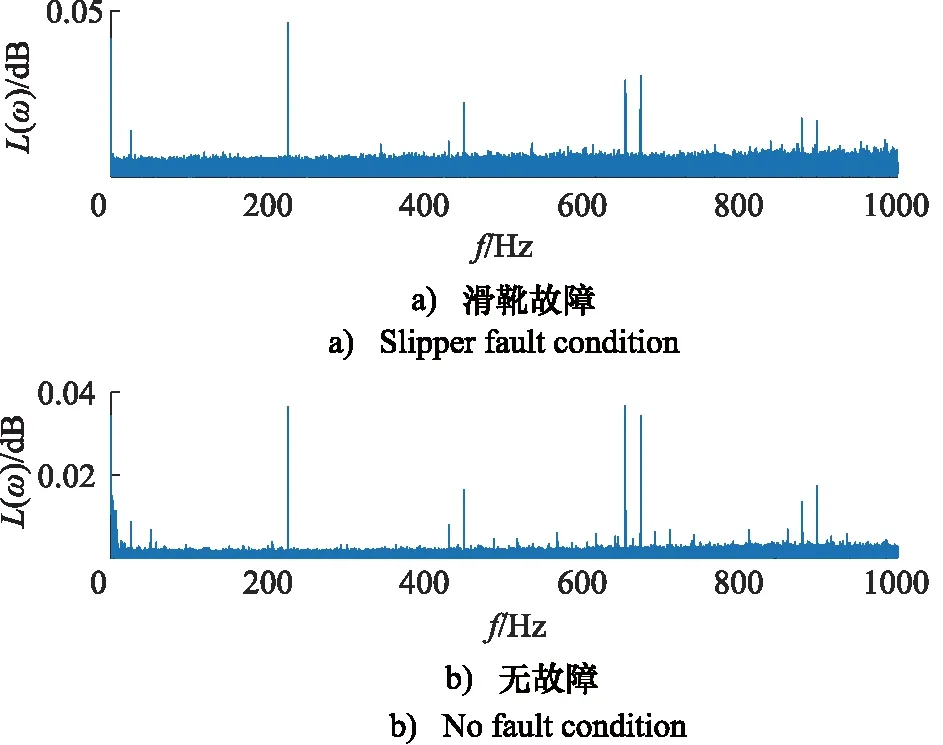
图10 滑靴故障和无故障状态下轴向振动信号频谱对比

根据使用传统信号提取方法快速傅里叶变换可得的频谱对比图可知，此时频谱图较为杂乱，无法准确定位故障的位置，因此对其进行进一步的小波包分析，根据小波包能量谱相关公式，得到的能量谱直方图如图11所示。

通过图11，可以看到滑靴故障与无故障状态下轴向振动信号各个频段能量谱之间的差值，此时与快速傅里叶变换相对比，可以更精准地确定故障位置，可以得知1号频段的能量相差比较大，接下来进行能量百分比的统计计算，滑靴故障时各频段序号对应的能量百分比如表2所示。

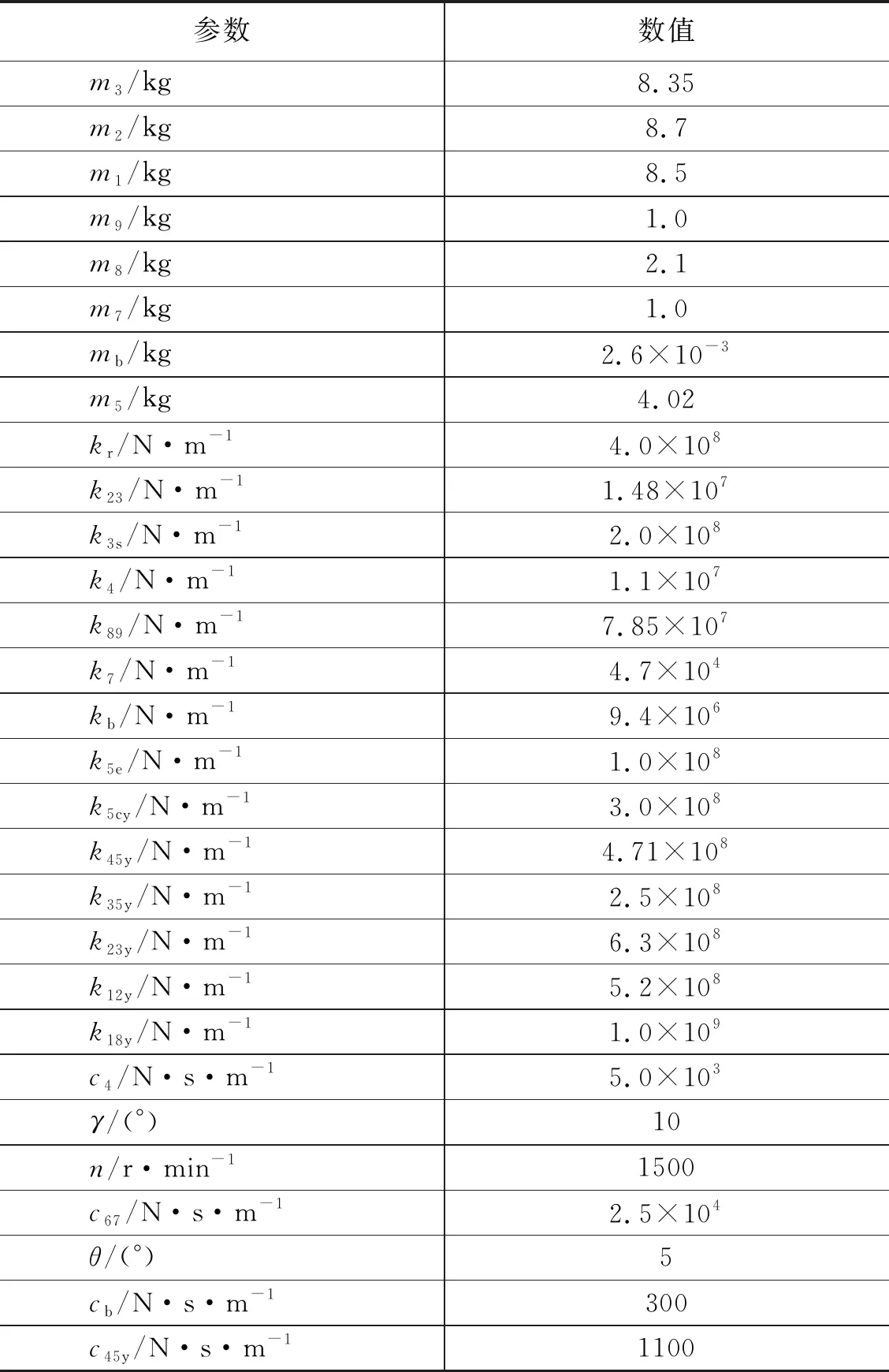
表1 双斜式柱塞泵滑靴故障仿真参数值

表2 滑靴故障时轴向信号各频段能量百分比

图11 轴向振动信号小波包分解子频段能量对比图

无故障时各频段序号对应的能量百分比如表3所示。

表3 无故障时轴向信号各频段能量百分比

正常与故障情况下，对应频段能量百分比之差(取绝对值)如表4所示。

表4 轴向信号各频段能量百分比差值

根据表4，对滑靴故障与无故障状态下轴向振动信号各个子频段进行对比，1号频段能量百分比差值最大，为5.55%，其次为4号频段，能量百分比差值为2.38%，差值最小的5号频段，能量百分比差值为0.20%。

1号频段能量百分比差值最大，但与其余频段对比差异不够明显，接下来分析径向信号的各频段能量差值。

2) 试验数据小波包能量谱径向信号分析

对在试验现场所采集到的原始滑靴故障径向振动时域信号和无故障状态下的径向振动时域信号进行分析处理，则首先需要仿真其时域信号，如图12所示。

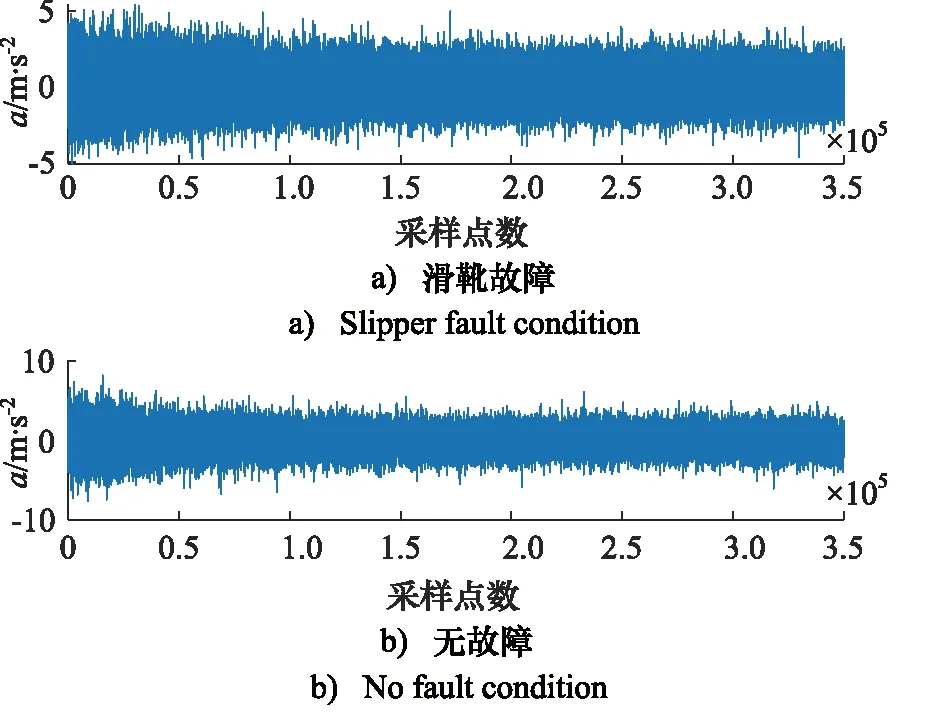
图12 滑靴故障和无故障状态下径向振动时域信号对比

接下来运用传统的特征提取方法快速傅里叶变换对原始时域信号进行分析，如图13所示。

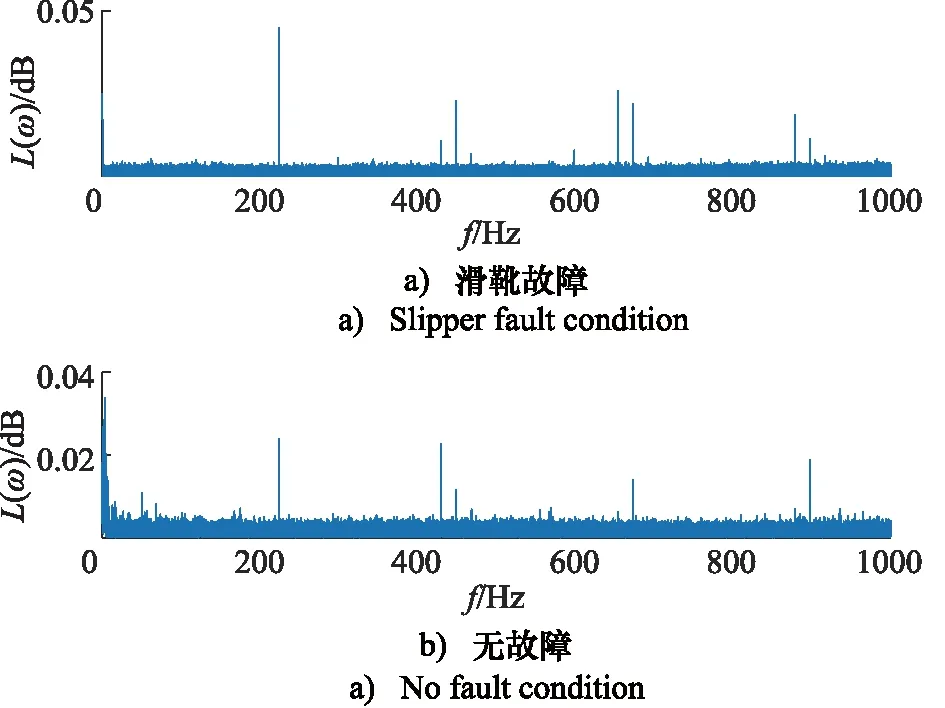
图13 滑靴故障和无故障状态下径向振动信号频谱对比

使用快速傅里叶变换对径向振动信号分析得到的频谱图也无法准确定位故障，同样采用小波包方法进行进一步仿真分析，如图14所示。

根据图14中的滑靴故障与无故障状态下径向振动信号各个频段能量谱之间的对比可知，也是1号频段的能量相差最大，为了得到进一步的精确分析结果，进行能量百分比统计。

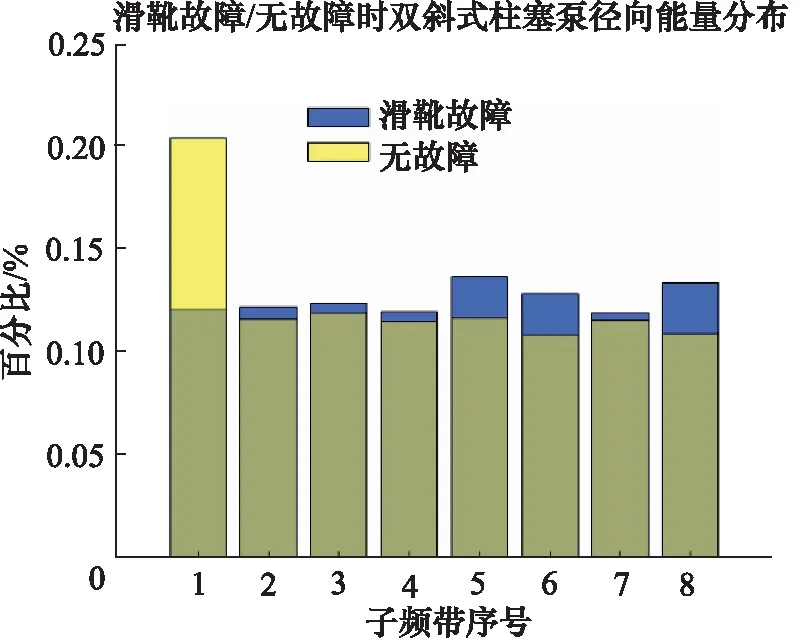
图14 径向振动信号小波包分解子频段能量对比

滑靴故障时各频段序号对应的能量百分比见表5。

表5 滑靴故障时径向信号各频段能量百分比

无故障时各频段序号对应的能量百分比见表6。

表6 滑靴无故障时径向信号各频段能量百分比

正常与故障情况下，对应频段能量百分比之差(取绝对值)见表7。

表7 径向信号各频段能量百分比差值

根据表7，对滑靴故障与无故障状态下径向振动信号各个子频段进行对比，1号频段能量百分比差值最大，为8.28%；差值最小的7号频段，能量百分比差值为0.35%。其中1号频段能量百分比差值最大，而且与其余各个频段的能量百分比差值比轴向振动信号时更为明显。为了更好地突出故障特征，接下来对轴向信号与径向信号进行信号能量增强来分析各频段能量差值。

3) 试验数据信号能量增强数据分析

根据前文提到的小波包能量谱叠加理论，对柱塞泵轴向与径向上振动信号各个频段的能量进行叠加，再使用能量增强处理后，来对比无故障状态与滑靴故障状态下的结果，如图15所示。

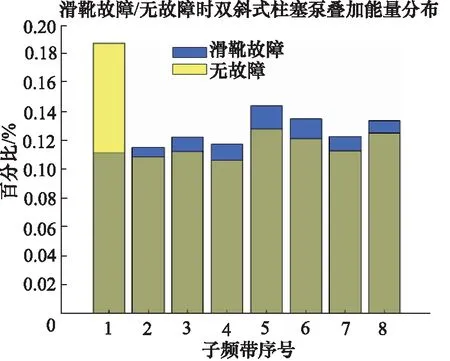
图15 振动能量增强小波包分解子频段能量对比

滑靴故障时各频段对应的能量百分比见表8。

表8 滑靴故障时叠加信号各频段能量百分比

滑靴无故障时各频段对应的能量百分比见表9。

表9 滑靴无故障时叠加信号各频段能量百分比

正常与故障情况下，对应频段能量百分比之差(取绝对值)见表10。

表10 叠加信号各频段能量百分比差值

根据表10所得数据，对滑靴故障与无故障状态下叠加信号各个子频段进行对比分析，可以得知1号频段能量百分比差值最大，为7.58%，超过了7%，其余各个频段的差值都在2%以下。因此，使用能量增强后的故障信号处理效果要优于使用传统小波分析方法单独分析轴向振动信号或径向振动信号。接下来对发生滑靴故障之后的故障特征频段进行分析,如图16所示。

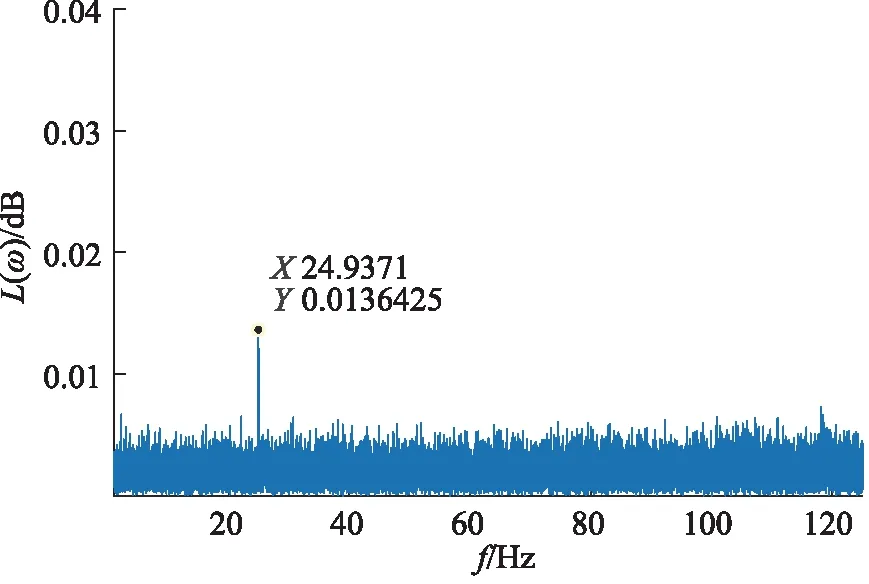
图16 滑靴故障特征频段的频谱图

经由试验信号能量增强数据分析以后，可以得知滑靴故障位于第1频段之内，绘制的第1频段滑靴故障特征频段频谱图中也可以得知，故障特征频率为24.9371 Hz，相比于传统的特征提取方法，本研究提出的基于振动能量增强的双斜式轴向柱塞泵滑靴磨损故障诊断方法具有更好的诊断效果。

4 结论

(1) 提出了一种基于振动能量增强的双斜式轴向柱塞泵滑靴磨损故障诊断方法。通过分析双斜式轴向柱塞泵机械振动机理，基于振动传递模型，确定了故障特征增强能量谱中的频率敏感范围。该方法可以减小环境噪声对诊断结果的影响，大大提高了双斜式柱塞泵滑靴磨损故障诊断的效果。

(2) 通过模型仿真与试验验证的对比，验证了滑靴磨损故障下理论模型的建立是准确的。基于小波包能量谱能量增强的故障诊断方法可以明显地提取出滑靴磨损时的振动信号特征变化。柱塞泵轴向与径向上振动信号小波包分解可知，皆为1号频段上能量差值最大，但是效果不够明显，使用能量增强故障诊断方法之后，效果明显，可以更好地突出故障。