基于托肯重演的并行结构过程模型修复方法
2023-02-24白二净李晓岩杜玉越
白二净,李晓岩,杜玉越
(1.青岛黄海学院 大数据学院,山东 青岛 266427;2.山东科技大学 计算机科学与工程学院,山东 青岛 266590)
0 引言
随着信息技术不断变革、信息资源不断增多,越来越多企业组织关注并使用信息管理系统,从而产生大量的事件日志。过程挖掘通过从企业信息管理系统实际产生的事件日志中提取有用信息,发现并改善实际过程模型[1]。过程挖掘技术[1-3]主要包括过程发现、符合性检查和过程增强三方面。过程发现[4]根据不同过程挖掘算法和实际事件日志来挖掘不同过程模型。原模型与实际产生的事件日志之间的不一致可通过符合性检查[1-3]来确定。当模型与事件日志不一致时,通过实际事件日志来修复或扩充模型则属于过程增强。随着对过程挖掘技术研究的不断深化,许多过程挖掘算法被提出。α算法[5]根据日志间的四种次序关系挖掘过程模型,但存有很多缺点,例如,α 算法要求日志的直接跟随次序关系是完备的,且不能处理重名任务、短循环、不可见变迁和非自由选择结构等。针对α 算法[5]的不足,文献[6-7]中提出了相应扩展方法。启发式挖掘算法在构建过程模型时,根据事件和序列出现频次[8]的高低,确定路径是否应该出现在模型中。Fahland 等[9]提出的模型修复方法为提高拟合度加入自环和不可见变迁,导致模型结构变得复杂且精度降低。基于语言的区域挖掘[10]技术,模型拟合度很高,但模型的健壮性有待提升。
衡量过程模型的标准有拟合度、精度、简洁度和泛化度4个指标[11]:拟合度是评价指标中最重要的,是事件日志中的迹在模型中重演能力的表征;精度是描述模型重演事件日志能力的另一个重要指标,一个精度相对比较高的模型,很少重演事件日志以外的其他事件;简洁度要求尽可能以简单的模型来展现事件日志;泛化度是描述模型扩展能力的指标,可以预测将来迹的发生情况。
当业务过程或环境等发生变化时,都会导致已有过程模型不能完全重演事件日志。应对这种情况,既可运用实际日志来挖掘一个全新的模型,又可以根据实际日志修复模型。新挖掘的模型存在丢失原模型原有优势的风险。模型修复是在原模型的基础上进行,既可以确保模型重演大部分日志,又不会破坏原模型的优势[12]。文献[13]中针对选择结构模型,提出了一种基于托肯重演的选择结构模型修复方法,通过托肯重演确定模型偏差所在位置,根据偏差位置采用逻辑Petri网来修复选择结构模型。本文在文献[13]托肯重演算法的基础上针对并行结构提出一种基于逻辑Petri 网和托肯重演的并行结构修复方法。逻辑Petri 网能很好地描述活动之间的逻辑关系,使得修复模型更加简洁,并且逻辑Petri 网在修复过程中能有效避免自环和不可见变迁,从而提升模型精度。目前国内有很多关于逻辑Petri 网的原理和应用的研究文献,文献[14]中提出基于逻辑数据Petri 网的业务过程建模与分析;文献[15]中提出基于逻辑Petri 网的选择结构修复方法。鉴于逻辑Petri 网的优势,本文在其基础上提出采用托肯重演的方式对并行结构进行修复的方法。首先通过托肯增强重演算法,计算模型与日志之间的偏差;然后根据偏差位置来修复模型。通过实验与Fahland 等[9]和Goldratt[16]方法对比,本方法具有比较高的拟合度和精度。
1 基本概念
本章简要介绍相关概念,元组、事件日志[6-9]、Petri 网[1-5]、逻辑Petri网[17]、工作流网[18]、过程树[19]及一些常用符号表示。
定义1元组[6-9]。x=(a1,a2,…,an)为含有n个元素的元组,其中第i个元素用πi表示,i∈(1,2,…,n)。
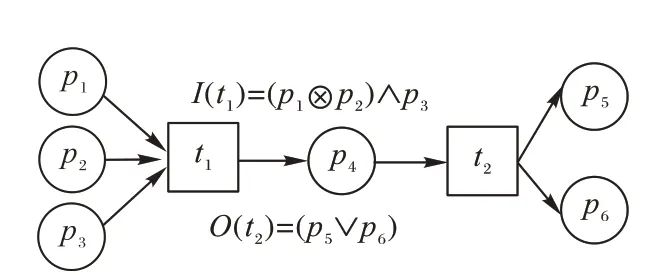
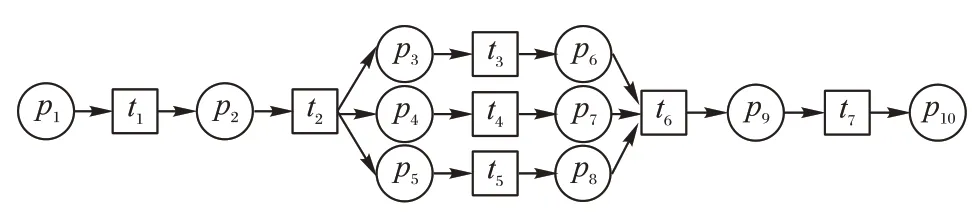
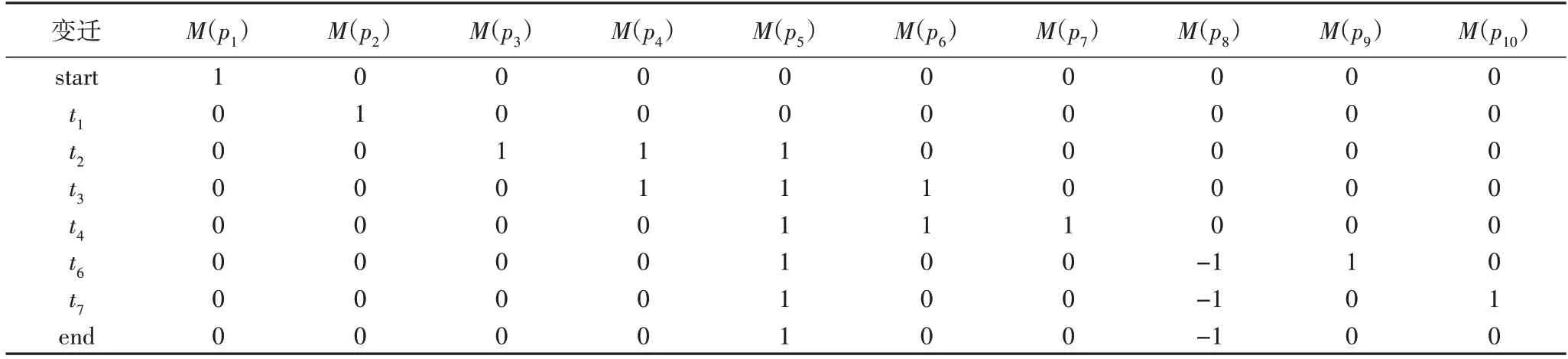
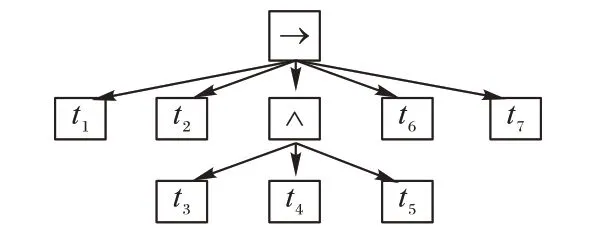
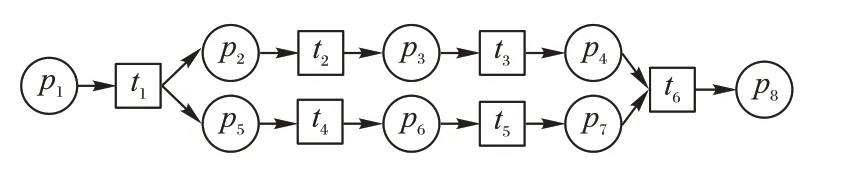
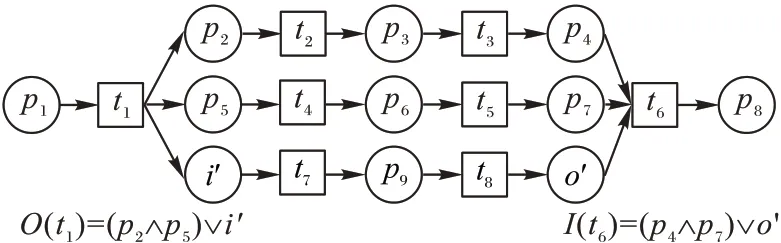
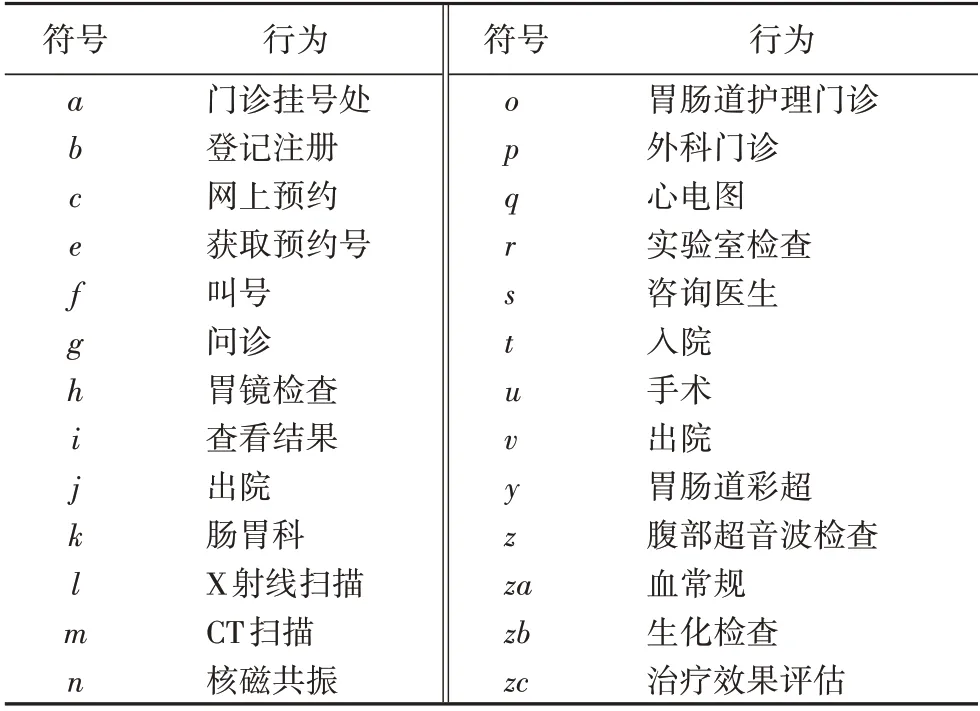
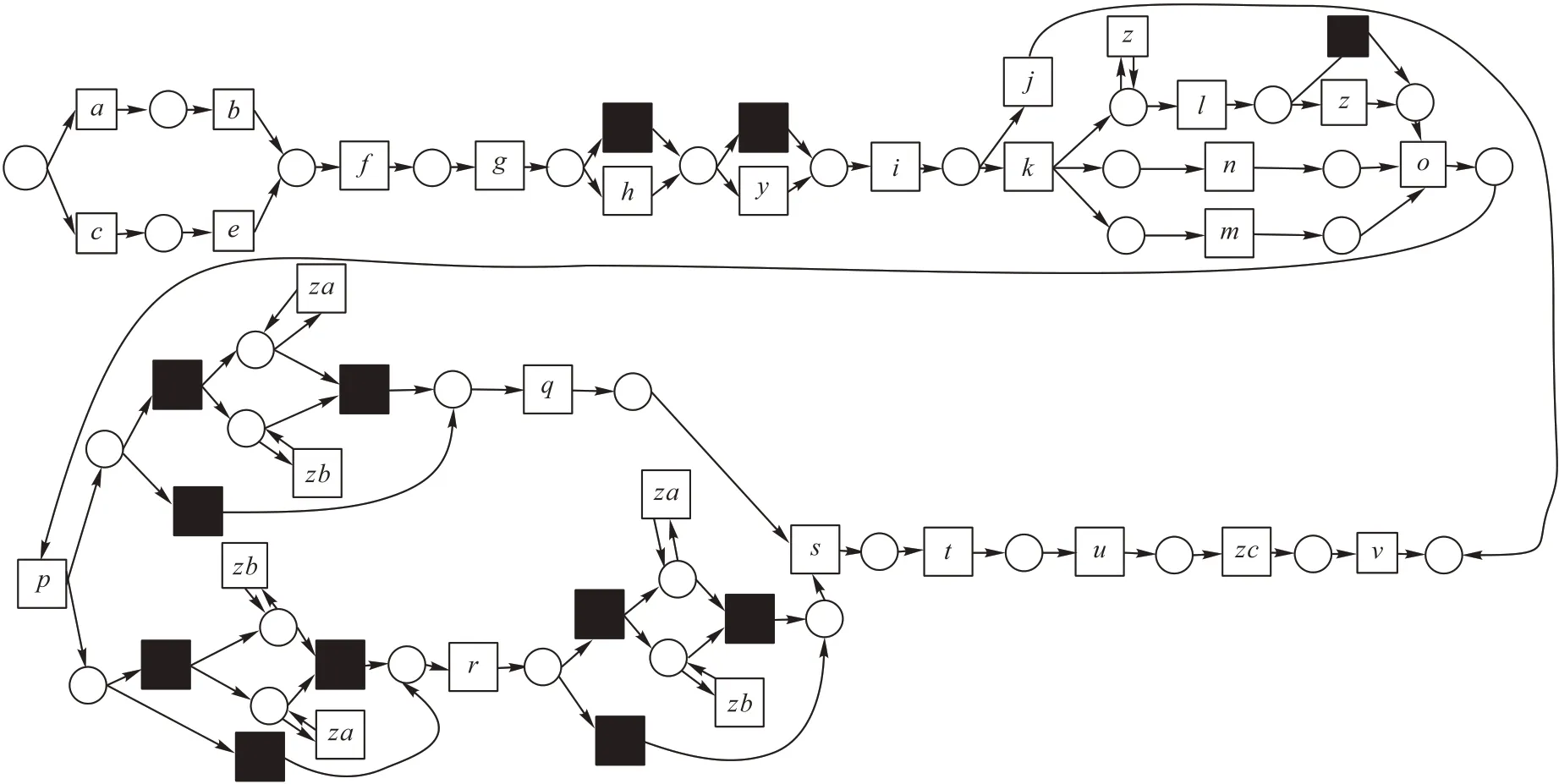
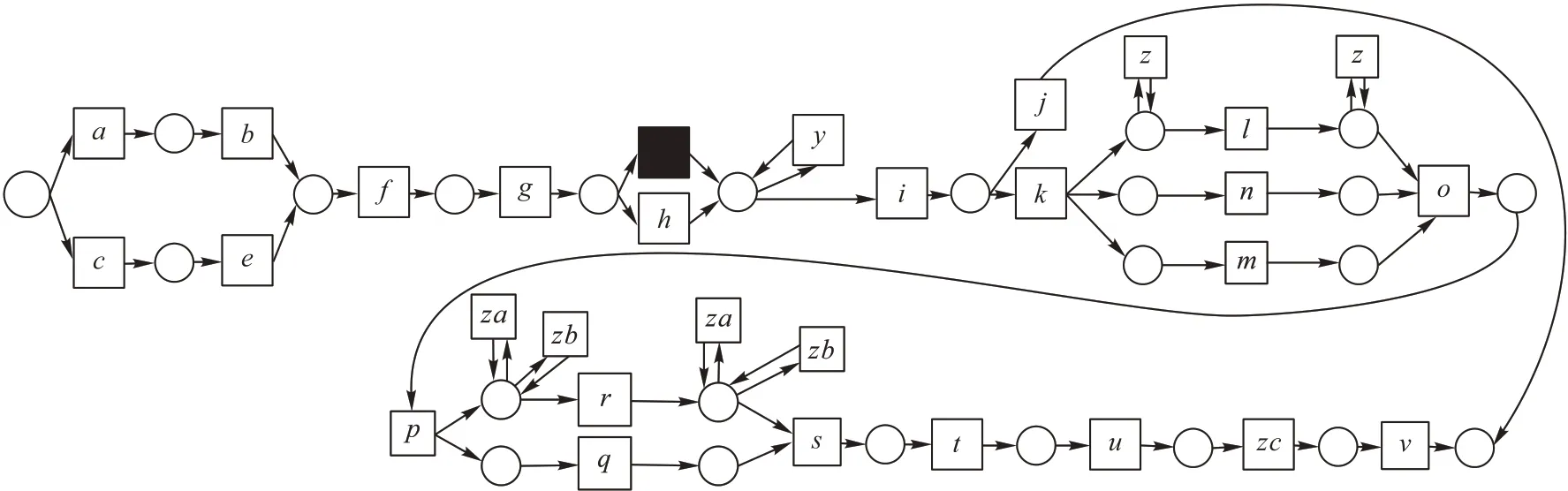
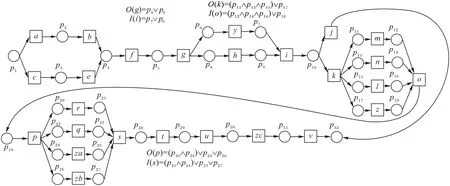
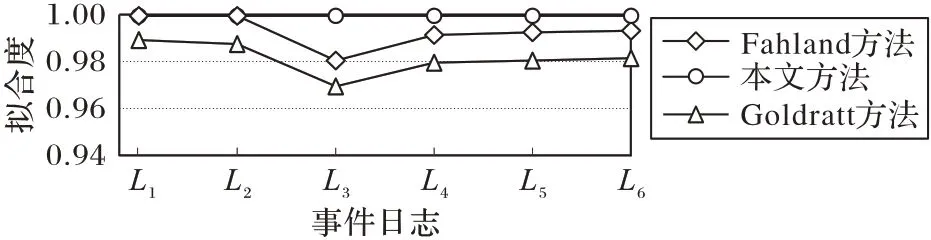
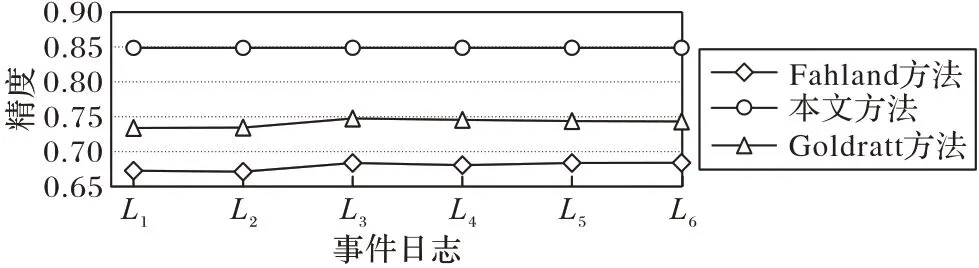
定义2迹和事件日志[6-9]。设A是活动集合,迹σ∈A*是活动队列,且1 ≤i 图1 所示为一个逻辑Petri 网。t1为逻辑输入变迁,I(t1)=(p1⊗p2) ∧p3是t1的逻辑输入函数,表示有2 种情况会触发t1。①p1和p3中存在托肯;②p2和p3中存在托肯。t2为逻辑输出变迁,O(t2)=p5∨p6是t2的逻辑输出函数,表示t2引发后会有3 种情况:①p5中有托肯;②p6中有托肯;③p5和p6中都有托肯。 图1 逻辑Petri网模型Fig.1 Logic Petri net model 定义8过程树[19]。设A是活动集合,⊕是给定的操作符集,τ 是不可见变迁,则有: 1)a∈A∪{τ}是一个过程树。 2)设PT1,PT2,…,PTn(n>0)是过程树,则⊕(PT1,PT2,…,PTn)也是过程树。 3)操作符集共有4种:×代表选择关系,其对应的子树选择其中一个发生;→代表顺序关系,其对应的子树会依次发生;∧表示并行关系,其对应的子树都会发生表示循环关系,其中PT1表示循环体会重复发生,PT2,PT3,…,PTn(n≥2)表示循环路径。 过程树是对工作流网的抽象表示,其中叶子节点代表活动,而非叶子节点代表活动之间的关系。 随着公司或组织规模不断壮大,管理信息系统逐渐新增或变更一些业务,从而产生新的事件日志。新产生的事件日志在原模型中进行重演时,因托肯缺失导致重演失败,因此原模型需要被修复。根据文献[13]将实际产生的事件日志在原模型中进行强制重演[20],以此来确定日志与模型之间的偏差,根据偏差位置来判定并行变迁是否并发执行,并根据结果来修复原过程模型。本文提出一种基于托肯重演的并行结构修复方法。通过托肯重演,确定原模型与实际事件日志之间的偏差,通过过程树计算并行变迁集合,然后基于逻辑Petri 网修复模型。 通过事件日志L在模型中进行重演[13,20],并计算重演过程中缺失的和遗留的托肯来确定模型的偏差位置。在并行结构中进行托肯重演依然会因缺少托肯使得托肯重演无法进行。因此,为确保托肯能从初始库所动态变化到终止库所,引用文献[13]中给出的增强重演算法,并以Petri 网并行结构为例,说明此算法在并行结构中产生偏差所在位置,以及后续修复方法。 算法1 增强重演算法[13]。 通过算法1 使工作流网中的托肯从初始库所,动态变化到终止库所,最后消耗终止库所中的托肯。在从初始库所到终止库所变化过程中,根据库所位置的不同采用不同算式计算M(p)的值。下面以日志L1中迹σ1为例,给出算法1 在并行结构中的执行过程。 图2 工作流网模型WFN1Fig.2 Workflow net model WFN1 在start 状态(初始状态)除M(p1)=1 以外,其余M(pi)=0。对于变迁t1∈T且p1∈⋅t1-t1⋅,所以M(p1)←M(p1)-1,而对于t1∈T且p2∈t1⋅-⋅t1,所以M(p2)←M(p2)+1。因此在变迁t1处M(p1)=0,M(p2)=1,其他库所处托肯值不变,以此方法计算后续所有变迁处库所托肯值,计算结果见表1。最后,M(p10)=0 代表重演结束。结束(end)后,M(p8)=-1 代表缺失的托肯,M(p5)=1 代表遗留的托肯。 表1 重演σ1的托肯值变化表Tab.1 Change table of token in σ1 replay 在原Petri 网并行结构中存在缺失和遗留的托肯,表示此并行分支并不是真的并发执行,需要对日志L1中其他迹继续进行强制重演。其他迹重演结果如与σ1强制重演后相同,则表示在σ1和σ2中的并行变迁是并发执行,否则是非并发执行。采用逻辑Petri 来修复模型,需增加逻辑输出函数和逻辑输入函数,需要计算模型中具有并行关系的变迁集合和并行结构开始和结束对。下面根据过程树,定义并行结构关系对、并行结构开始和结束对。 定义9并行结构对集合SCRP,并行变迁集合CT。设A是所有活动的集合,PT是工作流网WFN对应的过程树。CRP代表并行结构对,用元组(t1,t2)来表示。当∃N∈PT并且N=“∧”时,t1=⋅(⋅Nl),t2=()⋅,其中Nl和Nr分别代表并行结构的最左子树和最右子树。并行结构对集合用SCRP表示,SCRP={(t1,t2)|t1=⋅(⋅Nl),t2=()⋅,∃N∈PTandN=“∧”}。并行变迁集合用CT表示,CT={N.child,∃N∈PTandN=“∧”}。如图3 所示,CRP=(t2,t6),SCRP={(t2,t6)},CT={t3,t4,t5}。 图3 WFN1的过程树PT1Fig.3 Process tree PT1 of WFN1 算法2 计算并行结构对SCRP,并行变迁集合CT。 算法2 给出了计算并行结构对集合SCRP,并行变迁集合CT方法:步骤1)表示初始化CRP、SCRP和CT集合;步骤2)~17)当N节点是并行结构操作符时,并行结构开始和结束对存储于SCRP集合中所有具有并行关系的变迁存储于CT集合中;对PT中所有非叶子节点都重复执行步骤2)~7);当N为叶子节点时程序结束;步骤18)返回结果。 算法3 并行结构修复算法。 算法3 并行结构修复方法:步骤1)给LPN赋值;步骤2)调用算法2,计算并行结构对SCRP,并行变迁集合CT。步骤3)~14)对日志L中的迹σi进行强制重演,并将σi中含有剩余和缺失托肯库所分别存储于R1[]和M1[]中。步骤15)~25)对日志L中的迹σk进行强制重演,并将σk中含有剩余和缺失托肯库所分别存储于R2[]和M2[]中。步骤26)~45)计算σi和σk并行结构中第一个变迁、最后一个变迁,分别存储于CT[a]、CT[c]、CT[b]和CT[d]。步骤46)~63)计算逻辑输出函数O(t)和逻辑输入函数I(t)的值。最后一步返回修正后的LPN′模型。算法3 的时间复杂度为O(n3)。下面以L1为例给出基于托肯重演的并行结构修正例子。 图4 WFN1修复模型Fig.4 Repaired model of WFN1 算法3 只能修复日志动作与模型变迁相同的情况,而当实际日志动作与模型变迁不一致时,采用算法3 无法完成模型修复。过程模型在实际运行中因新增或变更业务,会产生新的事件日志,因此当日志与模型不一致时,日志动作经常比模型动作要多。针对这种情况,首先要挖掘由新增日志产生的子模型,然后再根据模型间的关系,将子模型插入原模型中,最后再修复模型。参考文献[13]给出映射函数的定义和计算新增日志动作的算法。 定义10映射[13]。对于日志L中的迹σ,若存在日志动作a∈&(σ),且存在模型动作t与日志动作a对应,则称Map(a,t)是日志动作到模型动作的映射。 算法4 计算子日志SL[13]。 算法4 计算出子日志[13]后,采用归纳算法挖掘对应的子模型。然后,根据子模型与原模型的关系将子模型插入原模型中。在插入模型时需要计算子模型与原模型的关系,具体算法见文献[13]。最后再根据算法3 修复原模型。下面给出含子模型并行结构修复算法。 算法5 含子模型并行结构修复。 图5 工作流网模型WFN2Fig.5 Workflow net model WFN2 运用算法5 修复WFN2,生成子模型WFN΄如图6 所示,修复结果如图7 所示。 图6 工作流网模型WFN΄ Fig.6 Workflow net model WFN΄ 图7 WFN2修复模型Fig.7 Repaired model of WFN2 对本文方法进行仿真实验和对比分析。实验中使用的事件日志和过程模型来自青岛某医院胃肠科。Fahland 等[9]方法对模型修复,是通过过程挖掘工具包ProM6.10 中实现,且可从http://www.promtools.org 网站下载。Goldratt[16]方法修复模型是在DOS 窗口下实现的。由于还没有逻辑Petri 网计算工具,本文方法的实现是通过手工模拟完成。 图8 Petri 网模型是根据事件日志用α 算法[5]挖掘得到,展示了患者从预约开始到就诊检查最后离开医院的整个过程。过程描述如下:首先患者可以直接到医院进行登记注册,也可以先通过网络预约后获取预约号;然后医生根据患者顺序进行问诊。问诊后,患者去做相应的胃镜检查,如果患者没有胃肠道相关疾病则离开医院;否则要在胃肠科做更详细的检查,相应的检查有X 射线扫描、CT 扫描和核磁共振;然后患者去外科诊所准备手术。手术前,需要进行的检查有心电图和实验室检查,然后病人被送进医院并进行手术,最后在经过治疗效果评估后,病人出院。 图8 胃肠道疾病患者治疗过程模型Fig.8 Process model of treatment of patients with gastrointestinal diseases 表2 是图8~11 中符号与实际日志动作对应关系。 表2 符号与行为的对应关系Tab.2 Corresponding relationship between symbols and activities 随着实际检查项目的增多,出现了新日志动作,原模型与事件日志间出现偏差。例如患者在做胃镜检查时,也可以做胃肠道彩超。此外,病人在前往胃肠科作进一步检查前,亦可选择腹部超音波检查。在外科门诊,患者除了心电图和实验室检查外,还需做血常规和生化检查。针对以上情况,采用Fahland 方法、Goldratt 方法和本文所提基于逻辑Petri 网托肯重演的方法对图8模型进行修复,修复模型分别对应图9~11。 图9 Fahland方法修复后的模型Fig.9 Model repaired by Fahland’s method 表3 所示L1~L6为实际产生的事件日志,包括信息有迹的数量与长度、事件数量、活动数等。 表3 事件日志Tab.3 Event logs 在本文修复方法中,根据实际发生日志,患者在门诊就诊时,可选择胃镜检查或胃肠道彩超或可都选择,增加逻辑输出函数O(g)=p6∨p8和逻辑输入函数I(i)=p7∨p9。患者在胃肠科进行检查时新增腹部超声波检查项,增加O(k)=(p11∧p13∧p15)∨p17和I(o)=(p12∧p14∧p16)∨p18。外科门诊、患者手术前还需做血常规和生化检查,增加O(p)=(p20∧p22)∨p24∨p26和I(s)=(p21∧p23)∨p25∨p27。 根据奥卡姆剃须刀原则[21],分析采用不同方法修复原模型后其简洁度。表4 给出三种方法修复后在增加库所、不可见变迁、自环等方面的对比。根据表4,本文方法增加8 个库所,而Fahland 方法增加11 个,Goldratt 方法因自环存在未增加新库所。从增加弧数量角度分析,本文方法增加12 条,而Fahland 方法和Goldratt 方法分别增加46 和16 条。从增加自环变迁数分析,本文方法未增加自环,而Fahland 方法和Goldratt 方法分别增加7 个。由此,可见本文相对于其他两种修复方法,其简洁度更高。 表4 三种方法的简洁度对比Tab.4 Comparison of simplicity among three methods 图10 Goldratt方法修复后的模型Fig.10 Model repaired by Goldratt method 图11 本文方法修复后的模型Fig.11 Model repaired by the proposed method 拟合度[22]是描述过程模型一致性检查最为重要的参数。根据不同数量级的迹,图12 给出了不同方法的拟合度对比。根据文献[22],可以计算出逻辑Petri 网模型的拟合度。由图12 可见,三种方法都有比较好的拟合度,均在0.9 以上,但Goldratt 方法略低一些。本文方法拟合度一直维持在比较高的水平。 图12 三种方法的拟合度对比Fig.12 Fitting degree comparison among three methods 图13 是三种修复方法在不同数量迹下精度变化曲线。本文所提出逻辑Petri 网模型精度根据文献[22]计算得到。Fahland 方法修复精度在0.68 左右浮动,Goldratt 方法修复精度在0.74 左右浮动,而本文修复方法精度在0.85 左右。因此,本文修复方法具有相对较高的精度。 图13 三种方法的精度对比Fig.13 Precision comparison among three methods 本文针对Fahland、Goldratt 方法等修复方法因加入自环、不可见变迁使模型结构发生变化、精度降低等问题,提出一种针对并行结构托肯重演的修复方法。当日志动作和模型动作一致时,通过增强重演来计算日志中缺失和遗留托肯值来判断原模型中并行变迁的关系,采用逻辑Petri 网的方式来修复模型。当实际的日志动作比模型动作多时,先根据新增日志动作计算子日志,再挖掘子模型;然后将子模型插入原模型中;最后在逻辑Petri 网的基础上结合给定算法进行修复。通过实验与Goldratt 方法、Fahland 方法进行对比分析,验证所提方法的拟合度与精度均相对较高。本文仅对并行结构进行了讨论,并未针对循环结构等进行讨论,这将作为今后研究的方向。

2 并行结构模型修复
2.1 模型修复








2.2 含子模型修复
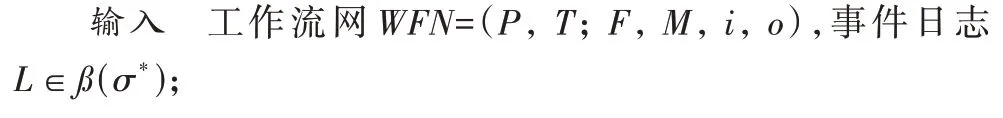
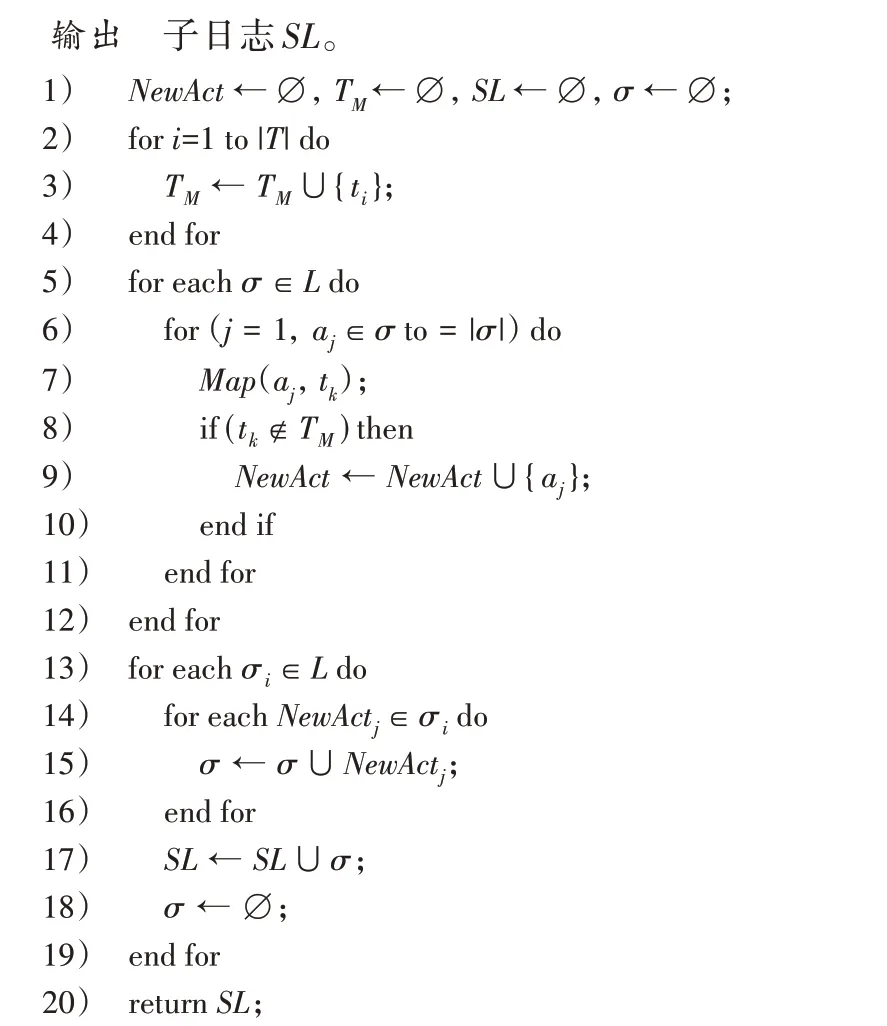


3 仿真实验
3.1 模型修复


3.2 模型评估

4 结语
