基于隐私计算的网络会议数字评选系统设计方案

王腾腾，崔 喆*，唐 聃

（1.中国科学院 成都计算机应用研究所，成都 610041；2.中国科学院大学 计算机科学与技术学院，北京 100049；3.成都信息工程大学 软件工程学院，成都 610225）

0 引言

数字经济转型中的信息社会时代，网络会议及其数字评选和评审已经越来越普及。尤其全球疫情以来，它渐渐成为人们日常工作生活的常态，如学位论文评选评优、项目评审打分排序、招标投标计票、合伙人网络会议决策表决、法院陪审团投票等。为方便表述后文也将评审专家称为“选民”，将评审专家的打分意见称为“投票”。目前国内已有多家厂商相继推出了各自的网络会议数字评选系统，如腾讯投票、腾讯在线文档评选、问卷星等投票产品，其基本功能模式为：主办方发起网络会议，邀请各方“专家”参会“投票”，即各方对于评选对象分别给出自己的数字打分意见并交由主办方汇总计算，由主办方单方面公布结果。代表专家评选意见的“投票”及其汇总结果通常采用整数或有理数的表达方式。目前各大厂商此类网络会议数字评选系统的工作原理及功能模式都大同小异，共同的问题是“选民”的“投票”隐私信息完全掌握在主办方手里，而“选民”却不容易判断统计结果是否公正可信。有的产品厂商宣称采取了“匿名”打分的措施，然而只是保证各位“选民”之间“投票”信息保密，而会议主办方和厂商均可看到每个投票者的具体“投票”信息。因此目前此类产品系统并未真正对评审专家的“投票”隐私信息实行切实的保护，导致评审专家在重大评选场合可能因担心隐私泄露而不做出公正的评审。此外，产品系统的这种工作模式下，主办方所公布的统计结果是否公正、可信，评审专家也常常存疑。从工作模式和技术原理角度看，造成问题的根本原因在于缺少隐私保护前提下参与者的协同计算技术措施。既要保护评审专家的个人意见隐私又要能通过合作获得安全可信的公正结果，是这类网络会议数字评选系统亟待解决的关键技术。在当今数字经济社会转型的信息化时代，该类隐私计算问题引人注目，具有比较广泛的意义。

近年来逐渐兴起的隐私计算理念为保护隐私数据安全和处理提供了新思路，Gartner 在发布的2021 年前沿科技战略趋势报告中将隐私计算列为未来发展的九大趋势之一［1］。安全多方计算（Secure Multi-Party Computation，MPC）是目前实现隐私计算的重要支撑技术手段之一，起源于1982 年Yao［2］提出的百万富翁问题，指一组互不信任的参与者之间在保护数据隐私的前提下完成协同计算的过程。如今MPC可以粗略分为三大类技术路线，即基于混淆电路技术的MPC、基于同态密码技术的MPC 以及基于秘密分享的MPC。

基于混淆电路的MPC 将目标函数表示为多元函数，进而把多元函数表示为布尔逻辑门电路，参与计算的各方各自对函数的一个变元进行秘密赋值，然后由门电路完成函数计算。自Yao 提出基于混淆电路的安全两方计算后，相继有学者提出改进协议：Goldreich 等［3］将两方扩展至多方，并采用随机比特串掩码代替混淆真值表；Kolesnikov 等［4-5］对异或门进行优化，减少了异或门加解密操作；Zahur 等［6］对混淆电路的真值表进行优化，减小混淆电路规模。上述优化在一定程度上提高了协议执行效率，但仍只能支持简单运算，并且在实际应用中其安全性保障只能通过布尔电路的硬件底层实现，开发成本较高。目前的通用MPC 框架并不采用严格的混淆电路方式实现［7］，而是采用与秘密分享结合的方式实现。

基于同态密码技术的MPC 允许各方直接在密文上进行特定代数计算，得出的结果与在明文上进行同样的操作并将结果加密一致。只支持单一运算的同态加密方案很早被提出，如RSA（Rivest-Shamir-Adleman）［8］可实现同态乘法，Paillier［9］可实现同态加法；直至2009 年Gentry［10］提出第一个全同态加密方案，方案基于理想格构造，并通过对噪声接近阈值的密文进行“刷新”解决了噪声增长对方案同态计算能力限制的问题，实现了任意次数的乘法计算；由于Gentry 方案出现后出现了很多经典的全同态加密方案，如基于算数电路［11］和布尔电路［12］的全同态加密方案。目前已有多种全同态加密方案，虽形式上简明、理论上完整，但是同时支持加法和乘法的全同态密码技术方法仍然过于复杂、尚难以广泛应用。

基于秘密分享的技术手段由于计算量小且通信量较低，对于构造多方加法和乘法运算有特别的优势。Beaver［13］基于秘密分享理念提出了“乘法三元组”，通过秘密拆分以及多轮通信实现了多方乘法。之后“乘法三元组”也被作为组件与混淆电路等技术相结合实现通用安全多方计算框架［7］，但上述框架适用于普遍计算，对于特定的应用场景并不能表现出很好的计算效率［7］。目前基于MPC 的网络会议数字评选系统多采用秘密分享的技术路线：仲红等［14］提出了秘密值随机拆分的矩阵传送安全多方求和协议，但该协议仅支持加法计算且不能抵御多方作弊的情况；张嘉诚等［15］采用同态加密结合秘密分享的方式实现MPC，但方案涉及多种密码学工具，并且需要公钥基础设施支持，布设成本高，难以实施应用。Hevia 等［16］采用同态ElGamal 密码体制设计了一个隐藏计票结果的电子评审协议，该协议通过验证计票结果是否在大于合格门限数值的集合中来判断项目是否通过评审，但方案涉及混合网技术，实用性并不高。

综上，MPC 是目前实现隐私计算的得力手段之一。现有MPC 的三大类技术途径都不同程度地存在计算复杂度较高、仅支持单一评审方式的问题。因此，其技术产品工程开发需要针对应用的具体场景来做具体的定制。

针对当前网络会议数字评选系统存在的问题，本文提出一种基于隐私计算的网络会议数字评选系统设计方案。方案既能保证评审人打分隐私数据不泄露给任何人，又能通过评审专家之间自主协作计算的途径获得正确可信的评选结果。方案实现隐私计算的工作重点是设计有理数域上的秘密加法与秘密乘法协议。协议的核心算法分两个阶段的步骤实现：1）借助里所（Reed-Solomon，RS）码之生成矩阵的编码计算阶段（秘密分享阶段）；2）借助编码矩阵之单调扩展矩阵的协同计算阶段（隐私计算阶段）。此外编码矩阵的校验矩阵可用于校正检查门限秘密分享阶段和隐私计算阶段是否有影子份额被篡改的作弊行为存在，只要出错或被篡改的份额数量小于等于(d-1)（d为RS 码码距）就可以被发现，这使得网络会议数字评选的MPC 具备了去中心化的纠错监督与防止作弊的机制特征。此外本文方案将评审数据的哈希值作为存根交给主办方存档，以便事后追溯对照验证，可防止抵赖。于是，校验矩阵和协同计算过程环节的存根可以帮助评审专家们以自主协作-互相制约的方式实现多方安全计算结果的可信验证和过程追溯。

1 预备知识

1.1 线性分组码与生成矩阵

定义1［17］如果码C是V（n，q）的n重k维子空间V（k，q），则称C为q元（n，k）线性分组码，简称线性码。当（n，k）线性分组码的最小距离为d时，记为（n，k，d）线性码。

定义2［17］如果在V（n，q）的k维子空间V（k，q）中选k个n重矢量为一组基｛gi｝（i=1，2，…，k），那么任意码字C∈C=V(k，q)可由基底｛gi｝的线性组合给出：

式（1）中把线性码C=V(k，q)的基底｛gi｝（i=1，2，…，k），按行矢量组成的k×n矩阵Gk×n称为线性码（n，k）的生成矩阵。

1.2 线性码的对偶码与一致校验矩阵

定义3［17］若C=V(k，q)是线性码，则称V(k，q)的正交补（零子空间）V⊥(k，q)=V(n-k，q) 为线性码C的 对偶码C⊥。

定义4［17］在V(n-k，q) 中任取n-k个基底h1，h2，…，hn - k，以hi为行矢量得到C⊥的生成矩阵H(n-k)×n则为线性码C的一致校验（监督）矩阵，简称为校验矩阵。

1.3 （k，n）门限秘密分享以及相关定义

定义5设s0为待分享的秘密值，Gn×k为编码矩阵，s0通过Gn×k编码后得到n个值A1，A2，…，An，将Ai记作影子份额或秘密份额。

（k，n）门限秘密共享最早是由Shamir［18］于1979 年提出，其基本思想为：秘密s由分发者D以某种方式分割为n份不同的秘密份额si（i=1，2，…，n），只需得到其中的k个或k个以上的秘密份额就可恢复出s，而任何少于k份份额的组合均无法获得秘密s的相关信息，更不能恢复出秘密s。

1.4 MDS码与（k，n）门限秘密分享

定理1［17］Singleton 界。对于一个q元域上（n，k）线性码C，其最小距离d满足d≤n-k+1。

定理2［17］对于一个q元域上（n，k）线性码C，若最小距离d能够满足Singleton 界d=n-k+1，则称该（n，k）线性码为极大距离可分（Maximum Distance Separable，MDS）码，MDS 具有最大的检错能力。

定理3［17］RS 码是在Galois 域GF（2w）上进行的域元素的多项式运算（包括加法和乘法运算）的编码方式，RS 码通常有两类：一类是范德蒙RS 编码，另一类是柯西RS 编码。范德蒙RS 编码的生成矩阵是范德蒙矩阵，柯西RS 编码的生成矩阵是柯西矩阵。设C为GF（q）上长度n为q-1 的RS码，则满足：

1）C的最小距离d满足d=n-k+1；

2）C为MDS 码。

RS 码是一种MDS 码，由线性码与秘密分享的特殊相关性可知［19］：范德蒙RS 码的编码译码过程在本质上与Shamir的（k，n）门限秘密分享中秘密分发以及恢复过程等价。

1.5 范德蒙RS码编码与译码过程

设α=(D1，D2，…，Dk)T为k维列向量，Gn×k为范德蒙生成矩阵，gi（i=1，2，…，n）为随机选择的不相等的整数，β=(C1，C2，…，Cn)T为编码后的码字向量。编码和译码过程如下。

1.5.1 编码过程

将α编码为n维列向量β=(C1，C2，…，Cn)T需左乘一个Gn×k，编码过程如图1 所示。

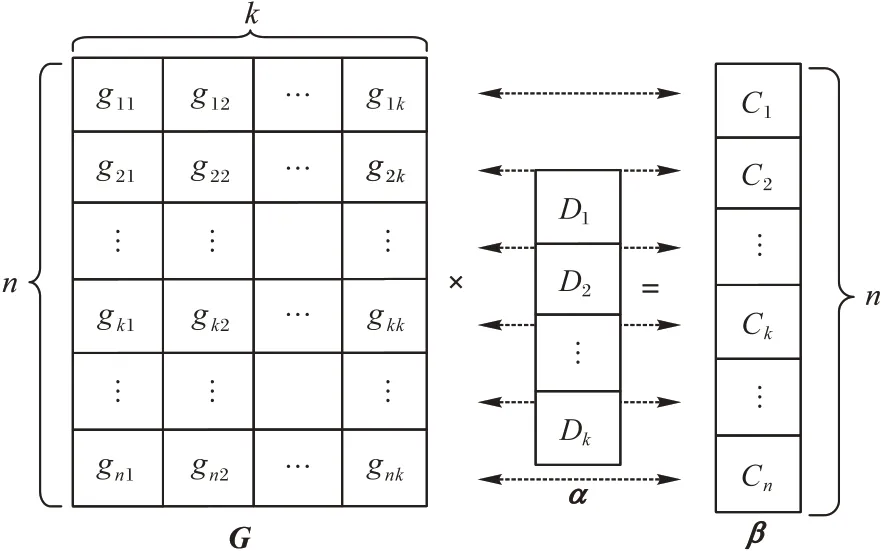
图1 编码过程Fig.1 Encoding process

1.5.2 译码过程

设β'=(C1，C2，…，Ck)T为在已知码字分量中任意选择k个元素组成的列向量，将β'中分量对应的G中的行筛选出来构成矩阵G'。由RS 码的MDS 性质可知，G'一定存在逆矩阵。译码过程如图2 所示。

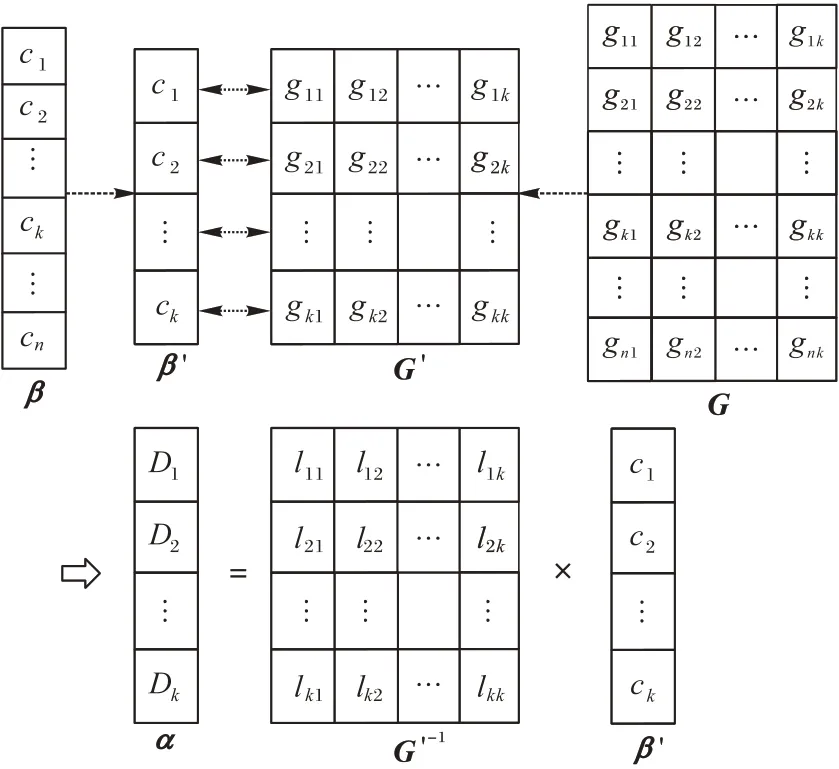
图2 译码过程Fig.2 Decoding process

2 方案相关协议

本文隐私计算协议本质上是一种基于秘密分享技术路线的MPC 协议。由于秘密分享与编码理论的特殊相关性［19］，借鉴文献［20］中用编码矩阵实现秘密分享的思想，本文进一步将文献［20］中有限域上的编码生成矩阵方法改为有理数域上的编码生成矩阵，从而获得一种有理数域上工作的秘密分享方法。其中生成矩阵的对偶矩阵用于检查纠正秘密分享中是否有错误的份额，而有理数域便于比较域元符号计算结果的大小从而更适合网络会议数字评选系统。本文编码矩阵生成的n维码字也恰好对应有理域上k-1 次插值多项式的（k，n）门限秘密分享体制所产生的n个份额。在此基础上本文利用单调扩张方法［21］，引入有理数域上生成矩阵的扩展矩阵，实现隐私计算。以下是方案相关矩阵和协议，n代表参与方人数，k为门限参数。

2.1 方案相关矩阵构造

本文通过构造范德蒙矩阵作为RS 码的生成矩阵G；通过GT×H=0 构造RS 码校验矩阵H；通过单调扩张方法得出扩展矩阵M。G、H、M构造如下。

算法1 矩阵构造算法。

2.2 秘密分享协议

设有n个参与方P1，P2，…，Pn，si为Pi的秘密值，Pi将si秘密分享过程如下（其中i=1，2，…，n，j=2，3，…，k）。

选择合适的门限参数k，输入秘密si得到Aij。

步骤1Pi通过算法1 得到生成矩阵Gn×k；

步骤2Pi选择k-1 个不相等的随机整数rij构造k维列向量αi：

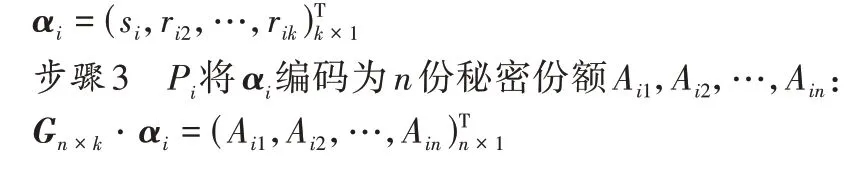
2.3 隐私计算协议

设有n个参与方，sa(a∈[1，n]) 为Pa的秘密值，Aa1，Aa2，…，Aan为Pa执行秘密分享协议后的秘密份额；sb(b∈[1，n]，b≠a)为Pb的秘密值，Ab1，Ab2，…，Abn为Pb执行秘密分享协议后的秘密份额；对sa和sb的隐私计算协议如下（其中i，j=1，2，…，n，i≠j，⊗为乘或加）。

步骤1Pi通过算法1 得到扩展矩阵M并求M-1；

步骤2Pi定义向量γ=(1，0，…，0)1×n并计算Ti=Aai⊗Abi发送给Pj；

步骤3Pi在本地计算Ti=Aai⊗Abi，并发送给Pj；

步骤4Pi构造向量η=(T1，T2，…，Tn)T；

步骤5Pi计算sa⊗sb=γ∙M-1∙η。

3 网络会议数字评选系统设计方案

3.1 方案实体

方案中涉及以下两方参与者。系统结构如图3 所示。

图3 系统结构Fig.3 System structure

1）评审人：具有评审权的人。

2）评审主办方：发起评审会议的主办方；验证评审人身份；保存评审人的评审数据哈希值。

3.2 方案应用场景描述

某单位现需多位评审人对项目进行评审打分，每一个项目有多个评分维度，例如经济效益、社会效益、可行性等评分项。为保证评审人的打分数据不被泄露给除自身以外的其他人，主办方不参与评审过程，只保存评审过程中的中间值以便后期对评审人评审行为可追溯。设评分项数为u，评审人打分完毕后得到评分列向量vi=(ci1，ci2，…，ciu)T，评审人取评分项平均值得到Vi（若评分项有权值并且无权值保密条件，则通过加权平均得到Vi），对Vi执行本文协议进行联合计票得到该项目的评分和，通过评分和或评分和均值判断项目是否通过评审。以上述场景为例描述方案执行流程。

3.3 加密以及数字签名方案

方案采用两方密钥交换协议协商加密密钥key，保证公共信道数据传输的安全性。需要保密传输时发送方用协商的密钥以及加密函数对消息m进行加密Ekey（m），接收方收到密文后再用相同的密钥对其解密Dkey（m）。

数字签名采用RSA 签名方案，签名方A 先用哈希函数计算消息摘要h（m），再用私钥d对其进行签名sigA(m)=h(m)dmodn，验证方B 收到签名后用签名方的公钥e完成验证：verB(m，sigA(m))=true ⇔h(m) ≡sigA(m)e(modn)。

在本文方案的总体设计中，采用了对秘密份额Ai加密的方式保证评审人两两间保密通信，但是在实际的应用场景下可综合考虑布设成本选择是否对Ai实行加密传输，因为Ai只是n个秘密份额中的一个，根据RS 码译码过程（图2）可知，只有泄漏的份额数超过k个，评审人隐私打分数据才会被泄漏，而在会议活动中邀请的评审专家大多是诚实可靠的，所以同时泄漏k个以及k个以上的份额概率较低。实际的应用场景下也可通过增大门限值k来增加方案的安全性（k增大，恢复秘密所需要的份额数越多，成功恢复的概率就越低）。

3.4 方案执行流程

方案的执行过程分为4 个阶段：初始阶段、评审阶段、计票阶段、公告阶段。方案中所涉及的符号如表1 所示。

表1 协议中的符号含义Tab.1 Meanings of symbols in protocol

3.4.1 初始阶段

主办方完成评审人认证和数据初始化。

步骤1 主办方为合法评审人发放唯一标识符IDi；

步骤2 主办方根据评审规模及安全性要求确定n、k；

步骤3 主办方通过执行算法1 得到Gn×k、Hn×m、Mn×n。

3.4.2 评审阶段

初始化阶段完成后，评审人进入评审阶段对项目评分，再通过秘密分享协议得到评分的秘密份额并发送给其他评审人。具体步骤如下。

步骤1Pi对项目评审打分得到vi=(ci1，ci2，…，ciu)T，根据评审方式对评分项进行计算得到Vi；

步骤2Pi计算Vi的哈希值并将对Vi的签名一起发送给评审主办方以供验证和存档：(sigPi(Vi||IDi)，h(Vi||IDi))；

步骤3Pi对Vi执行秘密分享协议得到秘密份额Aij（j=1，2，…，n）；

步 骤4Pi对Aij签名并将Aij发送给Pj(j≠i)：(sigPi(Aij||IDi)，Ekey(Aij||IDi))。

步骤5Pj验证签名：

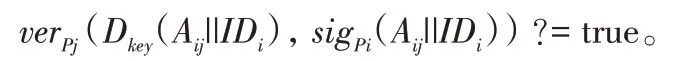
3.4.3 计票阶段

待所有评审人执行完评审阶段后，可进入计票阶段执行隐私计算协议进行联合计票（其中i，j=1，2，…，n，i≠j）。

步骤1Pi定义向量γ=(1，0，…，0)1×n；

步骤2Pi对秘密份额求和并签名，随后将签名与份额之和一起发送给Pj：(sigPi(Ti||IDi)，(Ti||IDi))；

步骤3Pj验证签名：

步骤4Pi构造向量η=(T1，T2，…，Tn)T并计算项目评分和V：

3.4.4 公告阶段

评审主办方和评审人在公告板上公布合法评审人ID 及计票结果V，评审结束。评审流程如图4 所示。

图4 评审流程Fig.4 Review flow

如果在保密权值的特殊应用场景下，则需要先将评审数据与权值相乘再求和，所以评审人需要先执行隐私计算协议秘密求得评分项与权值的乘积，再执行上述流程得出评分和。

3.5 评审人验证

在评审阶段步骤5 之后、计票阶段步骤3 之前评审人有可能会出现篡改他人秘密份额导致最终评审结果有误的作弊行为。例如Pi在评审阶段的步骤5 中收到了他人分享的秘密份额Aij，那么Pi可能会擅自篡改Aij导致份额之和T为错误值，最终影响评审结果的正确性，干扰评审的执行。

方案以大部分评审人都是诚实者为前提。每位评审人可在本地发现不大于n-k(n-k=d-1)个评审人的秘密份额出错或篡改行为存在。例如Pi质疑Pj、Pt(j≠i≠t)有篡改行为可通过以下方式验证(m=n-k)：

步骤1Pi将HT中的第j、t列筛选出来构成矩阵R。

步骤2Pi将η中剩余的Ti(i≠j≠t)构成列向量ξ。

步骤3Pi选择ξ中分量下标对应的HT中的列构成矩阵E。

步骤4Pi计算X=R-1∙(-(E∙ξ))。

步骤5Pi通过对比X中分量与计票阶段步骤3 中保存的Ti、Tt是否一致判断Pj、Pt是否有擅自篡改行为存在。

该阶段的实质是将Tj、Tt当作未知变量，通过上述过程重新求解出来，求解过程与纠删码的译码过程一致，验证过程示意图如图5 所示。

图5 验证过程Fig.5 Verification process

4 方案分析

4.1 正确性分析

方案中关键的计算步骤是可以用评分的秘密份额代替真实评分计算得出评分和。现对这一过程进行正确性分析。设参与方集合为{P1，P2，…，Pn}，可将参与方之间的协同计算简化为两两计算分析。设a0、b0分别为Pi、Pj的秘密值，正确性分析如下：

1）Pi、Pj通过编码矩阵Gn×k生成a0、b0的秘密份额。

分析可知fa（x）常数项为秘密值a0，fb（x）常数项为b0。

2）秘密分享后每个参与方都有a0、b0的一份份额，Pi、Pj进行“⊗”运算：

4.2 安全性分析

1）合法性：评审人需先通过评审主办方身份核验并获得唯一身份标识ID 后才可进行评审。

2）保密性：评审人通过秘密分享将秘密编码为n个秘密份额Ai1，Ai2，…，Ain并分发给其余评审人，每个评审人只有秘密值的一个份额，每个Pi在协议运行过程中只在本地对秘密份额进行操作，若有不诚实的Pi想恢复秘密值那么根据（k，n）门限秘密共享的完备性可知，需有k个及k个以上评审人合谋才能恢复出秘密值。实际方案执行时也可根据安全性要求具体的调整门限k。

3）可追溯性：评审人打分完毕后会将评审意见的哈希值发送至评审主办方存档；每一方得到的他人n个份额及其中间计算结果Ti都分别取哈希值保存在本地。若有评审人事后抵赖，可将评审意见取哈希值同评审主办方存档的哈希值对比防止评审人抵赖；也可要求评审人重新计算秘密份额并取哈希值同其余评审人保存在本地的秘密份额哈希值对比防止评审人抵赖。

4）防止作弊：由于RS 码为极大距离可分码，能够保证所能检查到的秘密份额分享错误或有擅自篡改行为的参与者人数最大为n-k(n-k=d-1)，即在协同计算过程中有n-k个及以下的参与者有作弊行为都会被发现。

5）健壮性：方案的（k，n）门限结构可提高系统的可靠性。在协议执行过程中，若评审人Pi未及时投票，那么其余n-1 位评审人Pj(j∈[1，n]，j ≠i)不会收到此评审人的秘密份额Aij，但仍可执行隐私计算协议计算参与者的评审数据之和，评审系统仍可正常运行，满足健壮性要求。

4.3 实验结果分析与对比

前两节中基于秘密分享和隐私计算协议给出了一种保护评审人隐私数据安全的网络会议数字评选系统设计方案，本节对此方案的执行流程进行实验模拟，验证方案的可行性以及不同评审规模下的计算效率，并且与同类型的相关研究进行对比。

1）实验前提：评分为十分制并且评分项无权值。

2）实验方案：实验数据设置是（n，k，u，v，G），其中k设置为；评分项u设置为5；在实验执行过程中生成u个随机整数构造向量v（v为评审人打分向量）；G中元素gi设置为1到n(gi=i，i=1，2，…，n)；规模n取10～60；通过不同的实验规模观察实验结果。由于初始阶段的时间开销移到了评审开始前，所以主要就评审、计票和公告阶段进行实验验证。测试结果如图6 所示。

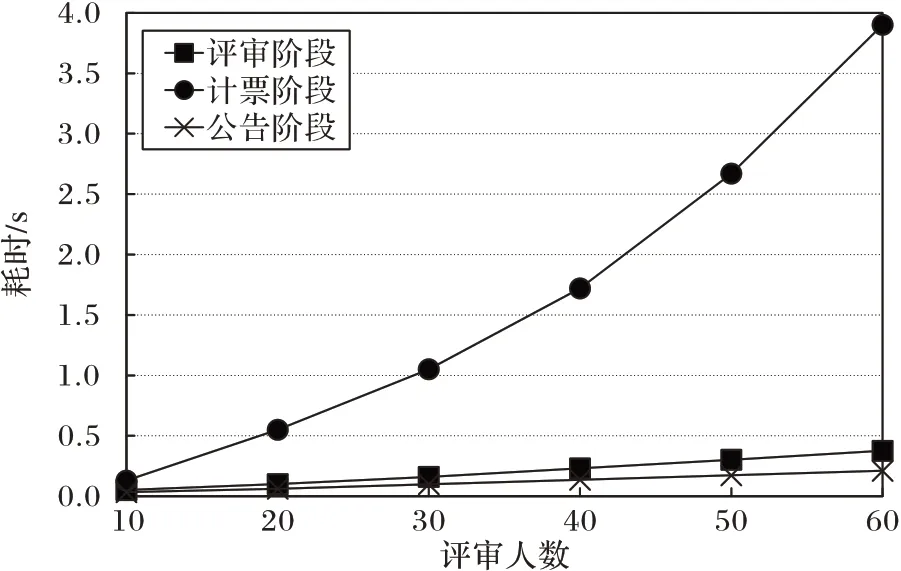
图6 不同评审人数量下的方案各阶段耗时Fig.6 Time consumption of each stage in scheme with different numbers of reviewers

3）实验结果分析：从图6 中可以看出，方案的整体耗时取决于计票阶段，这主要是因为在计票阶段需要对n维方阵M求逆，所以导致时间复杂度较高。从方案的执行流程角度分析：评审阶段每位评审人各自执行秘密分享协议得到秘密份额需执行O（kn）次整数乘法运算，发送秘密份额给其余评审人需进行n-1 次通信；计票阶段每位评审人对Aij求和需执行O（n）次加法，发送秘密份额之和给其余评审人需进行n-1 次通信，计算最终评审结果V（矩阵求逆再相乘）的时间复杂度为O(n2+n)。公告阶段评审主办方和评审人分别公布合法评审人ID 和评分和需进行2n次通信。因此可知对于每一个评审人来说方案的通信复杂度为O（n），时间复杂度为O(n2+n)。

4）对比分析：文献［14］提出的电子评审协议是通过对秘密值进行简单的随机线性拆分，评审人各自对份额相加实现MPC，但该协议仅支持加法并且安全性不足，无法抵御参与方作弊行为。文献［15］提出的电子评审协议通过同态ElGamal 密码体制对隐私集合求和，对私钥秘密分享使评审人只能联合解密计票结果，但该协议存在以下几个问题：1）多种密码学工具并用导致执行效率很低，其中的同态加密技术的算法复杂度更是随着评审规模的增长而呈指数型增长。2）方案安全性很低，没有制约参与方作弊的条件，仅靠评审人自觉执行；3）协议需要公钥基础设施的支持，布设成本高。文献［16］采用同态ElGamal 密码体制实现了隐藏计票结果的电子评审协议，该协议需借助m个混合网服务器对集合中c个元素进行随机置换，协议的计算复杂度为O((mc+n)p)（p为大素数位长），但若要保证协议安全性p至少为1 024，因此计算复杂度为指数级别，并且该协议还需要混合网服务器的支持，难以实施应用。

本文方案解决了上述评审系统所存在的问题：1）支持有理数域上的加减乘除运算，支持多种评审方式；2）具备纠查作弊行为的能力，满足一定的安全性要求；3）不需要公钥基础设施支持，实施成本低。

4.4 实例说明

本节通过对较小规模的评审实例展示方案执行过程中的数据。设评分为十分制并且评分项无权值，评审人数n=4，评分项数u=3，参数k=2，生成矩阵元素g1=1，g2=2，g3=3，g4=4，γ=(1，0，0，0)，评审人为P1、P2、P3、P4。设P1至P4的打分向量分别为v1=(6，5，4)T，v2=(3，5，4)T，v3=(6，8，4)T，v4=(3，5，1)T，采用简单的取平均值的方式得到V1=5，V2=4，V3=6，V4=3，设P1至P4的编码向量为α1=(5，2)，α2=(4，3)，α3=(6，1)，α4=(3，2)，接下来对V进行秘密求和。

1）方案各阶段执行时的数据展示。

①根据以上数据可得出G、H、M如下：

②评审人执行评审阶段得出秘密份额。

评审人将各自的秘密份额发送给其余评审人，因此P1拥有秘密份额（7，7，7，5），P2拥有秘密份额（9，10，8，7），P3拥有秘密份额（11，13，9，9），P4拥有秘密份额（13，16，10，11）。

③评审人执行计票阶段得出计票结果。

每位评审人计算本地秘密份额之和，P1计算得出T1=26，P2计算得出T2=34，P3计算得出T3=42，P4计算得出T4=50。评审人将各自的T分发给其余评审人，因此评审人可组成向量η=(T1，T2，T3，T4)T=(26，34，42，50)T，通过计算γ∙M-1∙η得出最终计票和V。

2）评审人验证阶段的数据展示。

如果P1质疑P3和P4有篡改行为，那么P1将HT中的第3列和第4 列筛选出来构成矩阵R，将HT中的第1 列和第2 列筛选出来构成矩阵E，构造向量ξ=(T1，T2)T=(26，34)T，定义X=(x1，x2)T，P1计算X=R-1∙(-(E∙ξ))=(42，50)T，与计票阶段步骤3 中保存的T3、T4一致，因此P3和P4不存在擅自篡改行为。R、E如下：

5 结语

基于MPC 协议的隐私计算在当今信息社会具有越来越广泛的需求。针对当前网络会议数字评选系统普遍欠缺合理技术措施对专家个人意见隐私保护的问题，本文提出了一种基于隐私计算的网络会议数字评选系统设计方案。该系统通过多方安全协同计算的途径，既能保证评审专家打分的个人意见隐私不泄露给任何人（包括会议主办方和其他评审人），又能通过评审专家之间自主协作的途径获得正确可信的最终评选结果。与已知的同类系统相比，该隐私计算系统的算法协议简明，执行效率较高，易于技术开发应用。此外，该MPC 隐私计算协议还使得评审系统的参与者能够通过自治协作的技术途径纠查作弊和防止抵赖，在一定程度上实现了去中心化的可信验证机制，这对其他隐私计算领域的迁移应用也具有借鉴参考意义。面对今后更大规模更广泛的应用场景，本文基于安全多方计算MPC 这种特定隐私计算方法在执行效率上仍然会有障碍，值得进一步改进。