中美股市跳跃溢出效应及跳跃对未来波动的影响研究
2023-02-24潘群星孙羽佳高天晴杜修立
潘群星,孙羽佳,高天晴,杜修立
(南京财经大学金融学院,江苏南京 210023)
一、引言
在“美国优先”政策的驱动下,美国经济形势曾一度向好,这种向好态势在股票市场上也有所体现。截至2020年2月14日,标普500指数的市盈率已经达到24.74倍,平均市净率超过3.65倍,创近十年以来新高。然而,突如其来的新冠疫情造成美国三大股指在2020年3月9日至18日间发生了4次一级熔断,美股市场成为疫情冲击的“重灾区”。同样受疫情的影响,上证综指在2020年3月份下跌了4.5%,第一季度累计下跌9.8%;沪深300指数在同年3月份下跌了6.4%,第一季度累计下跌10%;这些指数均创2019年5月以来最差月度表现和2018年第四季度以来最差季度表现。美国股市作为全球最大的股票市场,其动荡必然会对全球股票市场造成冲击;而作为全球第二大股票市场、第一大新兴市场的中国股市在反映美国股市等外围市场信息的同时,也具备了影响外围市场的能力(李红权等,2011)[1]。
股市作为经济发展的晴雨表,在疫情冲击下更能及时反映人们的行为和对未来经济的预期。疫情暴发初期,纷繁复杂的信息和严峻的形势造成投资者的恐慌情绪持续蔓延。据芝加哥期权交易所公布的信息,“恐慌指数”(VIX)①VIX指数是芝加哥期权交易所于1993年推出,它是以标普500指数期权的隐含波动率加权平均编制的。在2020年3月18日一度狂飙至85.47,为2008年金融危机以来最高位。不断扩散的恐慌情绪与经济活动的停滞可能会引起股市的大幅波动,而该波动又可分解为连续成分和跳跃成分。资产价格在短时间内出现非连续的大幅波动的现象被称为跳跃(Glosten和Milgrom,1985;西村友作和门明,2012;向健凯等,2017)[2-4],它包含上跳和下跳,这些跳跃由一个市场传递到另一个市场的过程就是跳跃溢出。
跳跃效应与传染效应是伴随金融市场的两种常规现象,特别是在危机暴发时期,一个国家金融市场的跳跃在传染的推动下将引起本国与他国相关市场跳跃(周伟和何建敏,2012)[5]。探讨疫情背景下中美股市的跳跃溢出以及跳跃对未来波动的影响,具有一定的意义。
第一,全球前两大经济体的股票市场在疫情期间都受到了极大的冲击,通过研究其跳跃溢出,可以发现最大的发达市场与最大的新兴市场在面临极端风险时是如何相互影响、相互作用的。
第二,研究疫情暴发前后中美股市跳跃溢出对投资者如何规避突发公共卫生事件造成的极端风险具有一定的指导价值。
第三,跳跃对未来波动率影响的预测有利于投资者做出正确的预判,对资产进行有效配置,以减少极端风险带来的损失。
二、文献回顾
国外学者对于跳跃的度量可以追溯到1967年,Press(1967)[6]提出了复合事件模型,他通过引入泊松过程来度量市场跳跃现象。Akgiray和Booth(1988)[7]对其展开了进一步研究,构建了混合GARCH跳跃模型。但上述模型都假定跳跃参数服从常系数泊松过程,并且认为跳跃强度和次数是跨期独立的,即一个时期的跳跃现象与前后不同时期价格的跳跃没有关系。随后,Kou(2002)[8]提出了一种价格及其波动率均存在跳跃现象的双指数跳跃扩散模型,借此来刻画金融市场的价格波动。任枫等(2009)[9]在此基础上构建了一种非对称双指数跳跃扩散模型,并提出基于马尔科夫链蒙特卡洛(MCMC)算法的模型求解,结果表明非对称双指数跳跃扩散模型能够更好地体现资产价格分布的尖峰厚尾以及有偏性特征。Duffie等(2000)[10]提出了收益与波动都存在跳跃的两种双指数跳跃扩散模型:跳跃独立随机波动率(SVIJ)模型和SVCJ模型。Eraker等(2003)[11]比较了随机波动率(SV)、随机波动跳跃(SVJ)、SVIJ和SVCJ等四种模型,发现SVCJ模型对金融资产的跳跃溢出有着最佳的拟合度。
关于跳跃溢出效应,国内也有一些学者利用SVCJ模型展开过探索。刘庆富和许友传(2011)[12]在研究国内外非同步期货交易市场之间的跳跃溢出时发现国内外期货市场存在显著的跳跃溢出效应,并且国内的跳跃溢出频度更高。宫晓莉等(2018)[13]通过构建广义双指数分布的跳跃扩散(GDED-SVCJ)模型研究了中国股指期现货市场的波动和跳跃特征,发现期货收益和现货收益上涨与下跌概率不对称,现货波动强度低于期货波动。王苏生等(2019)[14]运用SVCJ模型、傅里叶变换以及MCMC等方法分析了上证50ETF期权市场波动率的风险溢价,研究表明波动率溢价具有时变特征,在市场急剧动荡时期,投资者购买期权对冲波动风险的意愿较高。另外,Aït-Sahalia等(2015)[15]提出用Hawkes过程来捕获时间和跨资产的跳跃集群或金融传染,发现美国的跳跃往往在大多数其他市场得到迅速反应,而反向传播则不明显。由于该方法可以提供Hawkes过程的反馈方面,还可以提供跳跃导致更多的跳跃这一直观的因果解释,随后出现了一系列采用Hawkes过程来研究跳跃传染的文献,如陈淼鑫和徐亮(2019)[16]以及李福兴等(2020)[17]的研究。王茹婷等(2019)[18]则是选择日内跳跃Logistic模型对降噪后高频数据的日内跳跃情况进行检测。综上所述,关于收益率跳跃的研究是金融领域的一个热点问题。
为了模拟跳跃对未来波动的影响,Creal等(2013)[19]提出了一种基于得分函数的时变参数建模框架——GAS模型。该模型是一种观测值驱动模型,能够充分利用分布信息,且随机参数完全由过去的信息所预测。在GAS模型的框架下,不同的分布对应不同的得分函数形式以及形状特征。Bernardi和Catania(2016)[20]比较了基于不同分布的GAS模型以及其他模型的VaR预测效果,发现高度非线性波动率模型能提供更好的VaR预测。Harvey和Lange(2017)[21]考虑用厚尾分布(譬如,t-分布和广义误差分布)来发展GAS模型。淳伟德和赵如波(2016)[22]发现GAS-t Copula模型能够准确刻画上证综指隔夜收益与交易收益之间的非线性时变联动特征以及相依结构,而姚萍等(2020)[23]综合考虑了VaR的预测效果与计算负担,认为基于偏斜t-分布的GAS模型更加合理。
综上所述,国外学者对市场跳跃行为研究较早,通过加入跳跃因子来构建价格或波动模型(如SV、SVCJ等)并运用于金融市场进行实证的方法已经成熟,而且SVCJ模型在研究跳跃溢出方面具有一定的优势。国内学者对金融资产跳跃溢出的研究正处于起步阶段,在期货市场涉猎较多,股市之间的研究较少,并且基本都着眼于本国的股票市场,极少将我国股市与其他国家的股市相结合分析。关于跳跃对未来波动趋势有何影响的研究中,学者们主要运用不同分布的GAS模型对VaR进行了预测。此外,先前大多数相关研究没有针对特定的突发事件,研究结果未必适用当前的经济形势和国际环境。因此,在新冠肺炎疫情冲击的市场环境下,中美两国股市的跳跃风险是否存在相互溢出现象,以及由该冲击造成的跳跃对未来波动有何影响,都值得探究。鉴于此,本文以新冠肺炎疫情在全球蔓延为背景,采用SVCJ模型、GAS模型等对中美股市的跳跃行为进行考察,以期为优化投资策略及政府部门防控公共卫生突发事件造成的资本市场风险提供理论基础。
与现有研究相比,本文具有以下特色。
第一,国内很少有学者采用SVCJ模型来研究中美股市跳跃行为,该模型能够很好地描述收益率序列的跳跃式波动。本文基于该模型对跳跃溢出的概率、强度和幅度进行了刻画和分析。
第二,本文采用由GARCH类模型衍生的GAS模型来研究跳跃对未来波动的影响,是一种较新的做法。对于那些显著有偏或尖峰厚尾的数据,GAS模型的表现要优于传统GARCH类模型。
第三,考虑到疫情的影响和模型的稳健性,本文将样本区间划分为疫情暴发前期和疫情蔓延时期;考虑到中美时差问题,本文将日收益率划分为日内收益率和隔夜收益率。
三、研究方法
(一)基于MCMC算法的SVCJ模型
SVCJ模型是一种连续时间框架下的跳跃扩散模型,它假设资产的收益率和波动率都具有跳跃性质,基本形式如下:
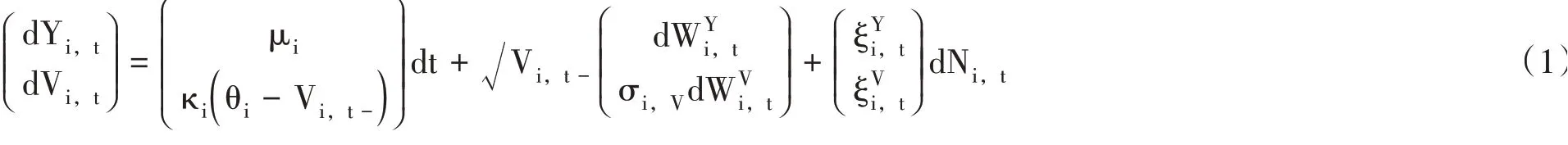
其中,“t-”表示无限接近于t的时间点,Yi,t是第i个资产在第t期的对数收益,Vi,t是第t期的波动率,μi代表期望收益率,ki表示波动均值回复的速度,θi是波动均值回复的平均水平,σi,V用来衡量“波动的波动”。当σi,V较大时,收益率序列存在厚尾性的特征。和表示瞬间相关系数为ρi的标准布朗运动,参数ρi反映资产i的收益率与波动率之间的相关关系。Ni,t服从强度为λ的泊松过程。ξYi,t和分别表示在Ni,t下的收益率与波动率的跳跃项。
当采用贝叶斯的MCMC方法对SVCJ模型进行估计时,要对式(1)进行Euler离散化处理。时间间隔为Δ的离散形式为:

其中,Ji,( t+1)Δ衡量是否实现跳跃,服从强度为λ的伯努利分布,取值0或1。与是相关系数为ρi的标准正态随机变量,其他参数与原模型同义。
MCMC算法是以贝叶斯模拟为基础对参数进行估计,克服了传统模拟方法中高维、静态等不足。式(2)中存在多个待估未知参数,使用贝叶斯方法“点估计”这些参数的关键在于求出联合分布函数F( V,J,ξV,ξY;Θ)。借鉴宫晓莉等(2018)[13]、刘庆富和许友传(2011)[12]以及曾昭法和左杰(2013)[24]的做法,本文使用吉布斯(Gibbs)抽样的方法,以获得一条收敛的马尔科夫链。
本文重点讨论的是中美两国股市收益率的跳跃溢出效应,故对每个市场存在的隐含跳跃次数J的估计十分重要。借鉴Johannes等(1999)[25]的做法,我们将J的“点估计”定义为:

其中,J(j)代表每次模拟的跳跃概率,M代表模拟跳跃的次数。注意到,Ĵ不是一个由0或1组成的向量,而是在t时刻跳跃到达的后验估计概率。当跳跃出现的概率小于阈值时不发生跳跃,记为0;相反,发生跳跃,记为1。借鉴Asgharian和Bengtsson(2006)[26]的做法,本文将阈值设定为隐含跳跃和估计跳跃之间的最小平均间隔,它与λ的测算是基本相同的。为了使两个市场所得出的数据具有可比性,本文采用同一阈值——各样本λ的平均值。
(二)条件跳跃溢出概率、强度及幅度
基于SVCJ模型及MCMC算法的估计结果,本文依旧借鉴Asgharian和Bengtsson(2006)[26]的做法,采用以下3个指标测度中美股市之间的跳跃溢出效应。
1.条件跳跃溢出概率
条件跳跃溢出概率(CJSP)是指市场之间传播跳跃行为的可能性,即当一个市场发生跳跃时引起另一个市场在同日或次日发生跳跃行为的概率。若测度美国股市对中国股市的跳跃溢出概率,则选取美国股市作为基准;反之,选取中国股市作为基准。其表达式如下:

其中,同日(次日)跟随跳跃的次数是指同日(次日)是否跟随基准市场发生跳跃,若发生记为1次,若不发生则记为0次。
2.跳跃溢出强度
跳跃溢出强度(JSI)是指市场之间传播跳跃行为的强度,即一个市场发生的跳跃引起另一个市场发生跳跃的程度大小,具体表现为两个市场发生的跳跃占整个样本的比重,表达式如下:

3.平均跳跃溢出幅度
平均跳跃溢出幅度(ASJS)是指市场之间产生跳跃溢出的平均幅度。若i代表中国股市,j表示美国股市,则中国股市和同日跟随其发生跳跃的美国股市的平均跳跃溢出幅度的表达式如下:
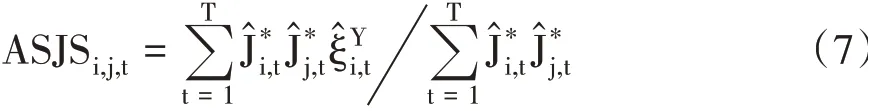
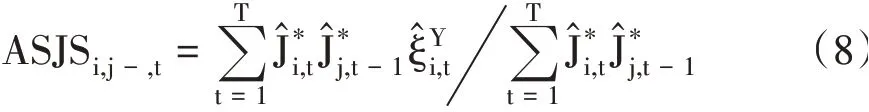
中国股市和滞后一日的美国股市的平均跳跃溢出幅度的表达式如下:其中为中国股市在收益率中的潜在跳跃大小,当时为上跳,当时为下跳。
(三)GAS模型
GAS模型是在GARCH环境下处理跳跃对未来波动率影响的一种方法,它依赖于扰动at的非正态分布和条件方差σ2t=Var(at|It-1)的GARCH型方程。GAS(1,1)模型如下:
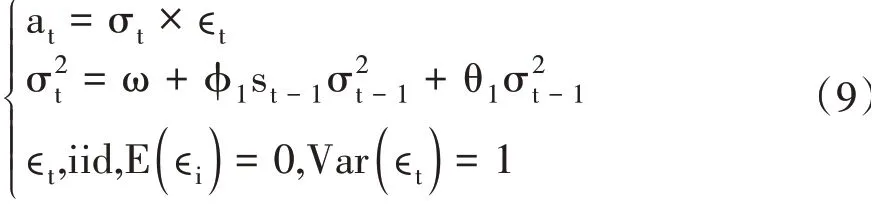
其中,st是条件得分函数,It是直到t时刻的信息集。
如果at服从t-分布,则:
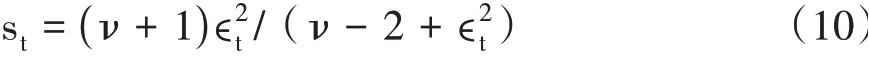
如果at服从广义误差分布,则:
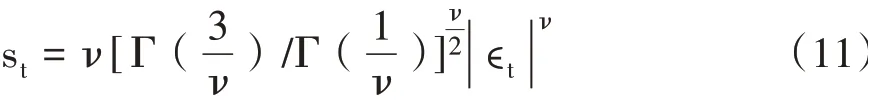
其中,Γ(·)表示Γ-函数。
如果at服从偏斜t-分布,则:

在给定t时刻以及过去信息的条件下,GAS模型可以根据似然度和密度来改善模型的局部拟合,并且能够较为直观地更新参数。更值得一提的是,GAS模型的得分分数由完整的密度结构来决定,而并非观测值的一阶或二阶矩。这些正是GAS模型与其他观测驱动模型的不同之处,也是更完善的地方。因此,本文选取GAS模型来测度中美股市跳跃行为对未来波动的影响。
四、实证结果分析
(一)数据
本文选取2017年6月1日—2022年9月19日的上证综指和标普500指数的日开盘价和收盘价作为原始数据。考虑到两国的法定节假日差异以及两市的开盘时差因素,本文剔除了两市未同时交易的数据,并将日对数收益率分解成日内和隔夜收益率,具体如下:
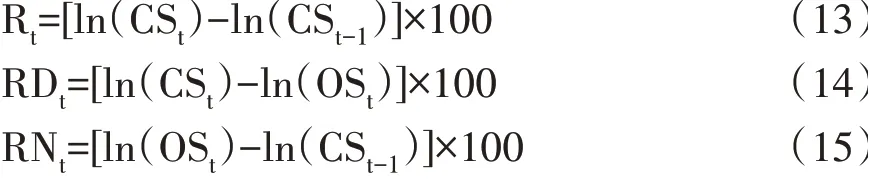
其中,CSt和OSt分别表示第t日的收盘价和开盘价,Rt、RDt和RNt分别表示第t日的对数收益率、日内收益率和隔夜收益率,上证综指的日内收益率与隔夜收益率分别记为SSRDt和SSRNt,标普500指数的日内收益率与隔夜收益率分别记为SPRDt和
SPRNt。
本文还以2020年1月21日——美国公布首例新冠肺炎病毒感染为时间节点,把全样本期分为新冠肺炎疫情暴发前期与新冠肺炎疫情蔓延时期,表1报告了基本统计量。由此判断,在疫情暴发前后以及全样本时期,均存在中国股市日内收益率大于美国股市以及美国股市隔夜收益率大于中国股市的规律,并且上证综指日内收益率的均值大于隔夜收益率,而标普500指数正好相反。这些可能与中国股市采用T+1而美股市场采用T+0的交易制度有关。对此,张兵和薛冰(2019)[27]得到过相似的结论,他们认为在T+1交易制度下,中国市场隔夜收益率为负的现象十分稳定。在疫情的冲击下,上证综指和标普500指数的日内收益率显著下降,隔夜收益率却有所上升。疫情的暴发使中美两国股市收益率的标准差都有所上升,但因抗疫力度不同,上证综指标准差上升幅度小于标普500指数,扭转了疫情前A股市场波动强于美股市场的现象。两市收益率分布始终呈现有偏、尖峰厚尾特征,J-B统计量的检验结果也印证了这一点。此外,由ADF方法检验可知,在三个样本期内,所有收益率序列都是平稳的,这意味着可以直接对它们建模,无须变换。
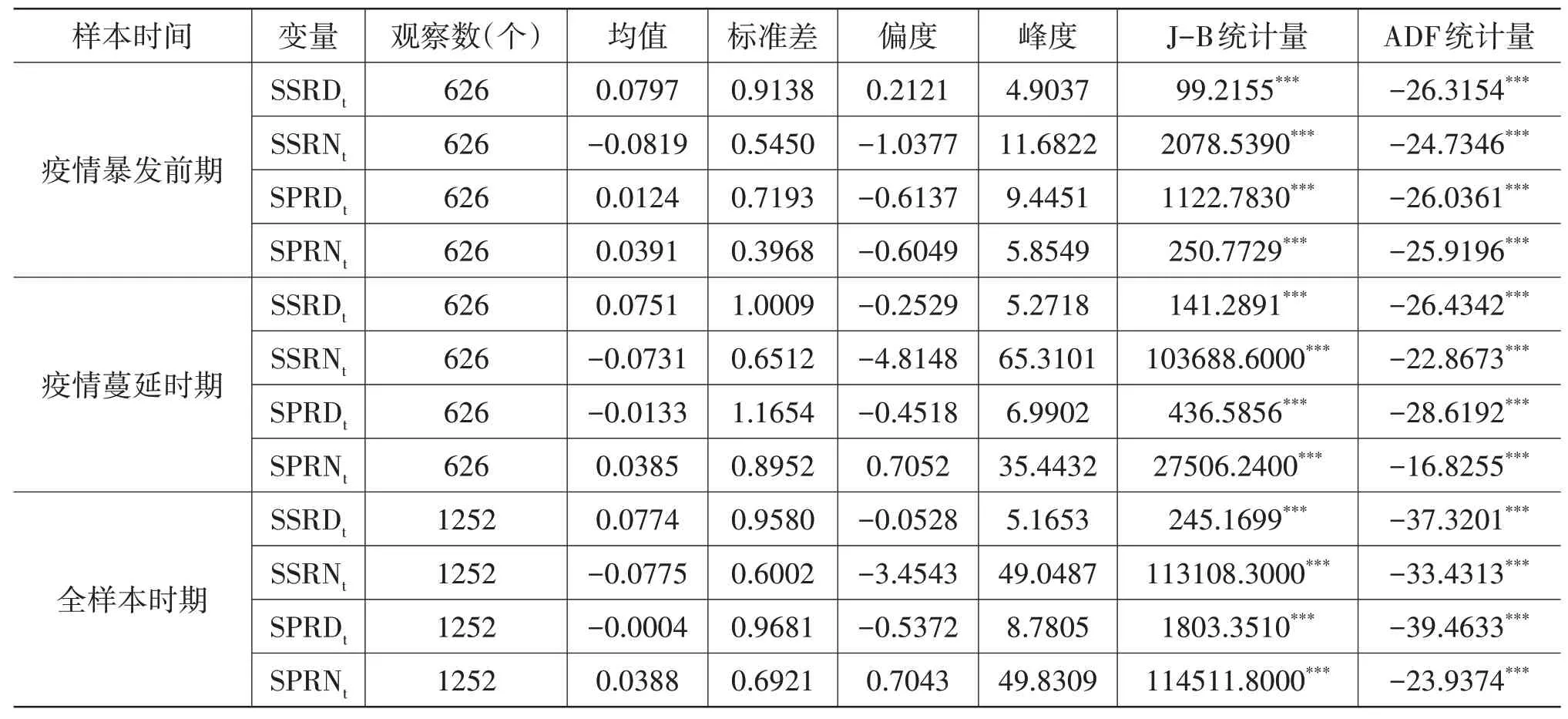
表1 上证综指与标普500指数日内和隔夜收益率的基本统计特征
为了更加直观地看出世界前两大经济体股市在新冠肺炎疫情冲击下的波动情况,本文绘制了日内和隔夜收益率时序图,如图1和图2所示。
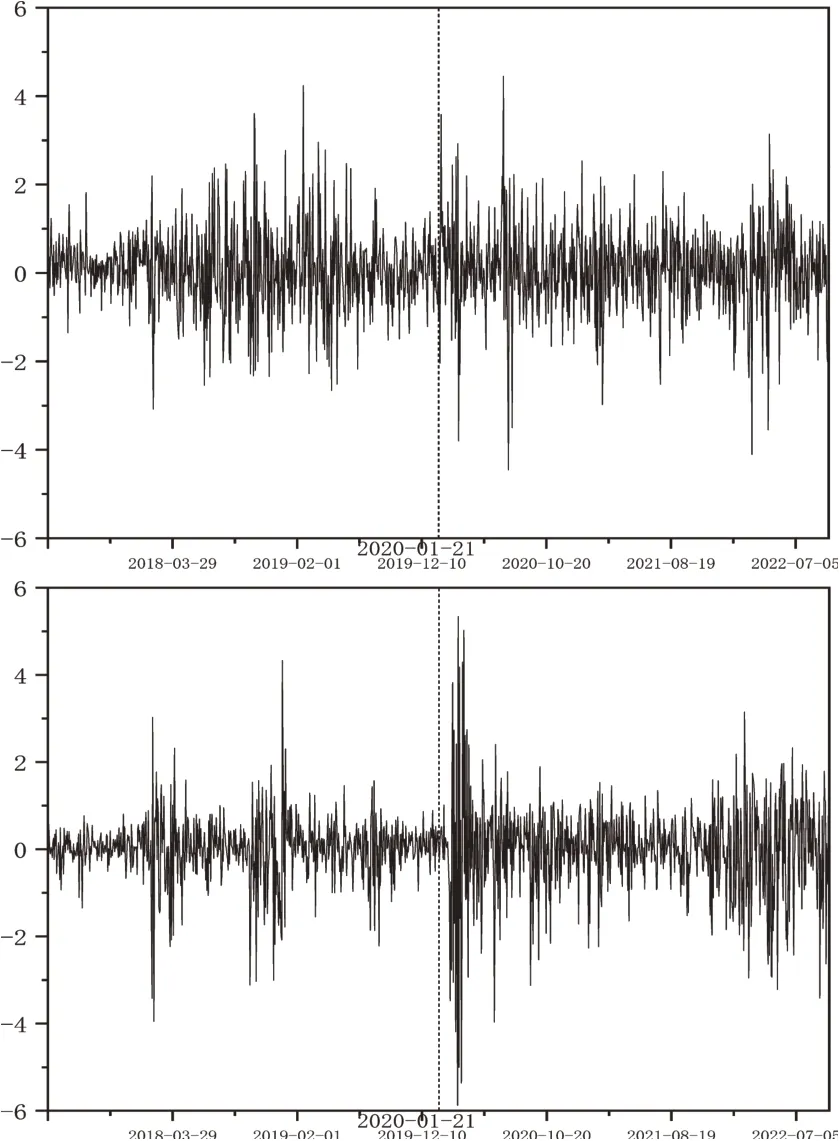
图1 上证综指(上)和标普500指数(下)日内收益率的时序图
从图1和图2可以看出,无论是日内收益率还是隔夜收益率,在全样本期内,中美股市的数据均呈现出聚集性;从波动的剧烈程度来看,隔夜收益率较日内收益率更加平稳;此外,两市收益率的走势趋于一致,具有一定的联动性。疫情暴发之前,上证综指的收益率波动比较剧烈,尤其是日内收益率,这可能与中美贸易摩擦有关;疫情暴发后,收益率序列出现了剧烈的波动和明显的上跳与下跳。疫情暴发之前,标普500指数除了贸易摩擦期间存在短暂波动外,其余时间走势较为平稳;受到疫情的冲击后,美股日内收益率与隔夜收益率均出现了显著的剧烈波动。尤其是在美国暴发疫情初期,极端情况更为明显,这说明疫情确实给美国股市造成了非常严重的冲击。
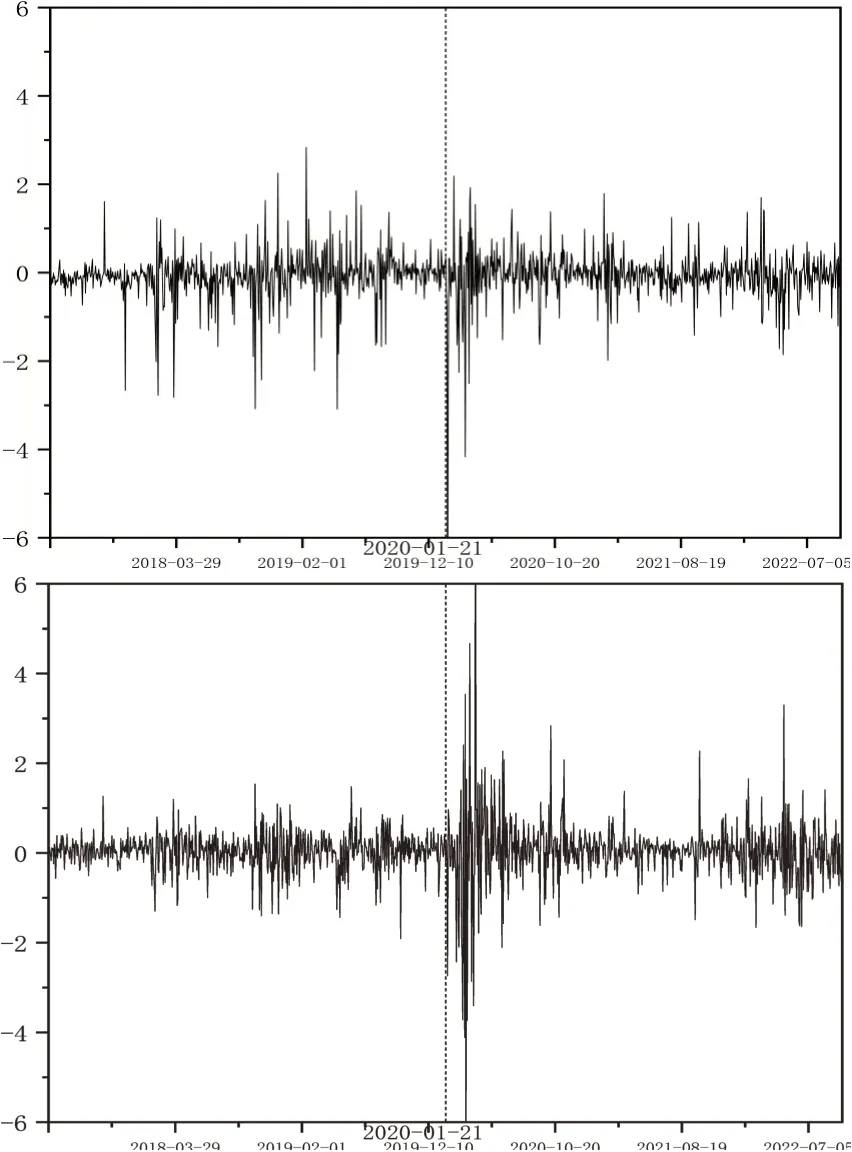
图2 上证综指(上)和标普500指数(下)隔夜收益率的时序图
(二)SVCJ模型的估计结果
基于MCMC算法估计SVCJ模型,在迭代6万次,并“燃烧”前面1万次后所得参数估计结果如表2所示。每个参数的标准差和MC误差都较小,且样本路径图中所显示的待估参数抽样值的走势与均值基本一致,表明该样本基本符合马尔科夫链的收敛准则,SVCJ模型拟合有效①篇幅所限,样本路径图没有展示,可向作者索取。。
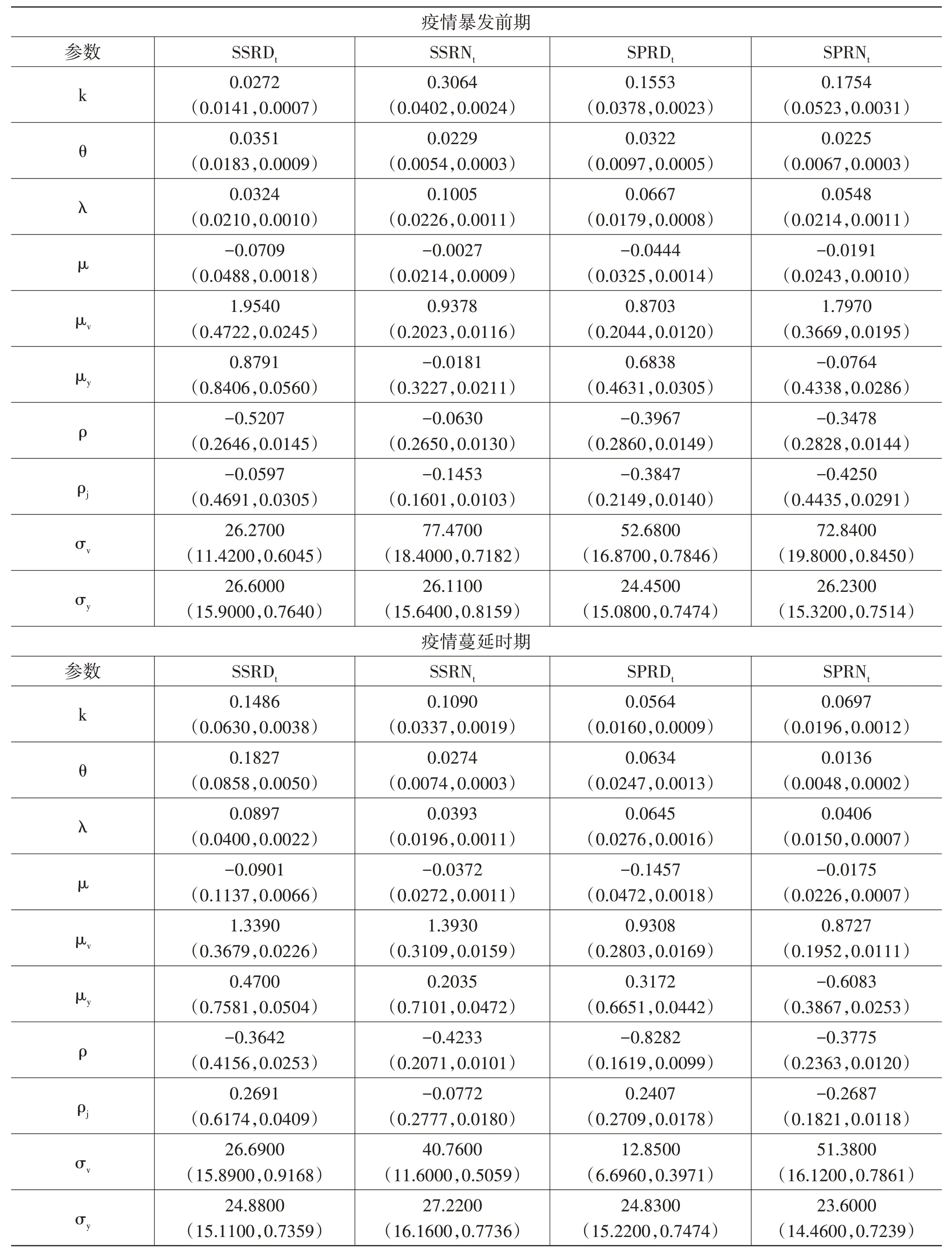
表2 SVCJ模型的估计结果
借鉴刘庆富和许友传(2011)[12]和Li等(2017)[28]的做法,定义每个市场收益率跳跃的绝对平均幅度为其中,ρj是的相关系数,利用后验均值估计结果进行计算。在疫情暴发前期,中美股市日内跳跃的绝对平均幅度分别为0.7624和0.3490,隔夜跳跃的绝对平均幅度分别为0.1544和0.8401。在疫情蔓延时期,中美股市日内跳跃的绝对平均幅度分别为0.8303和0.5412,隔夜跳跃的绝对平均幅度分别为0.0960和0.8428。研究发现,在疫情的冲击下美股市场日内跳跃和隔夜跳跃的绝对平均幅度均有所上升,而A股市场隔夜收益率跳跃的绝对平均幅度明显低于疫情之前。就跳跃强度而言,根据λ值,疫情暴发前,日内跳跃强度A股市场低于美股市场,隔夜跳跃强度A股市场高于美股市场;而在疫情暴发后,情况完全相反。由此,疫情对两国股市的跳跃幅度和跳跃强度均有影响,但是对同日和次日的影响结果不尽相同。由ρj的估计值可知,同一市场的收益率与波动率之间几乎都存在负向的跳跃相关性。三个样本期的ρ估计值均为负,这表明中美股市各自收益率与其波动率的扩散项之间存在杠杆效应,即利空消息对两个市场产生的影响要大于利好消息。

续表
(三)跳跃溢出效应测度
由SVCJ模型中J(j)的估计值①篇幅所限,具体估计值没有在表中呈现,可向作者索取。,结合公式(3),可以计算出疫情暴发前后上证综指和标普500指数发生跳跃的次数,如表3所示。
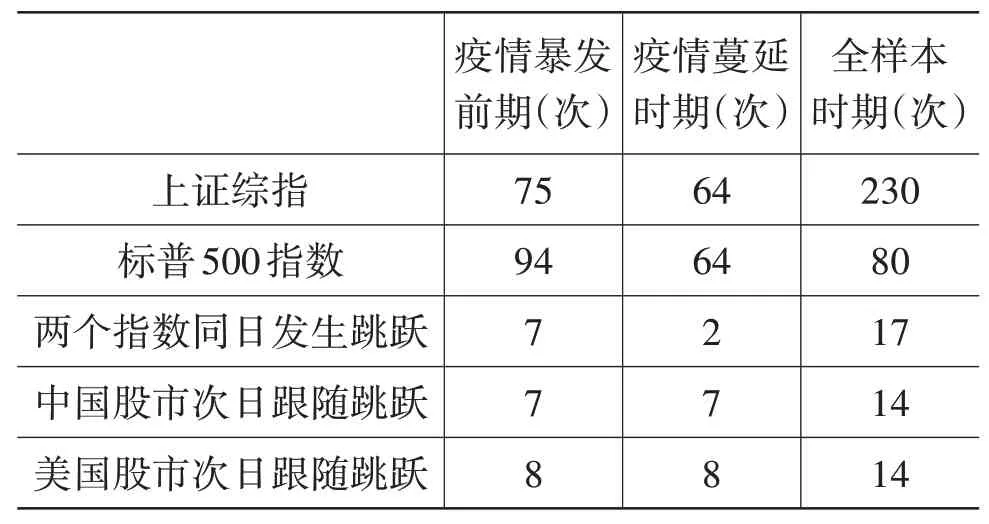
表3 发生跳跃的次数
研究发现在三个样本期内,中美股市的收益率序列均存在跳跃成分。在疫情暴发前,上证综指的跳跃次数小于标普500指数;而在疫情的冲击下,两者的差距明显缩小,上证综指与标普500指数的跳跃次数达到相同水平。虽然疫情发生后两个市场发生跳跃的次数或多或少有所下降,但是由于疫情暴发前期的样本里包含了中美贸易摩擦时期,且该时期较长,对疫情暴发前的跳跃次数影响较大,因此不能否认疫情的冲击会使跳跃行为更容易发生。此外,上证综指和标普500指数在三个样本期内次日跟随跳跃的次数始终持平,有理由相信中美股市之间存在信息互溢的情况,而不只是简单的单向溢出。于是,接下来可以运用CJSP、JSI和ASJS等指标去测度中美股市之间的跳跃溢出效应。
1.条件跳跃溢出概率
选取CJSP指标测度三个样本期内中美股市之间的条件跳跃溢出概率。表4展示了同日和次日的溢出概率。
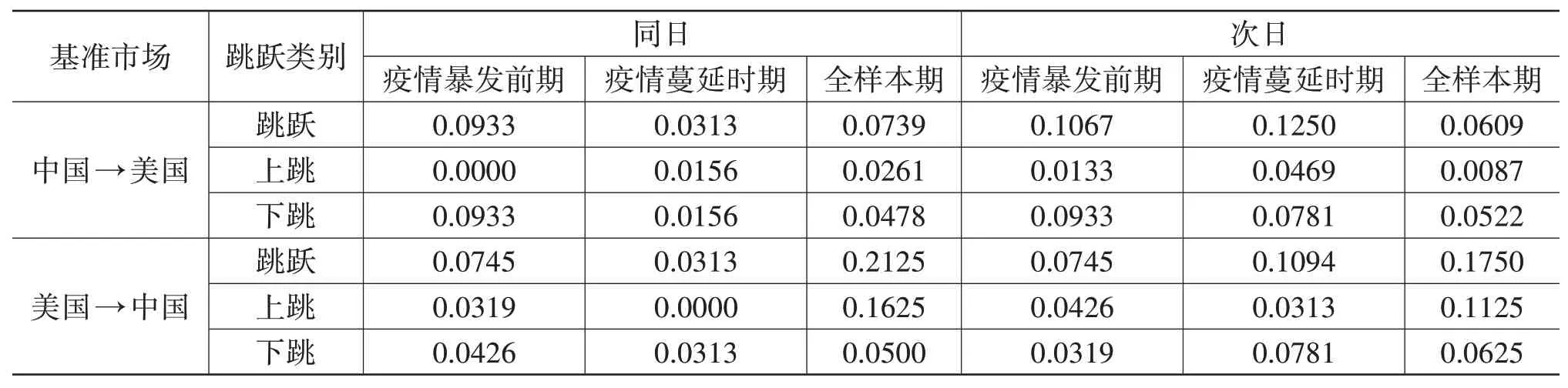
表4 条件跳跃溢出概率(CJSP)
纵向上看,受疫情的影响,无论是中国股市还是美国股市,同日的CJSP都有所下降,而次日的CJSP都有所上升,这意味着疫情暴发后中美股市滞后一天跳跃溢出的概率在增强,相较于疫情暴发前对对方市场跳跃信息做出反应所需的时间变长。另外,美股市场在疫情影响下的次日CJSP显著大于同日CJSP,这可能是由于疫情后A股市场上最大的活动发生在美股市场关闭的时候。但源自A股市场的跳跃信息的传递时效并未受疫情影响,始终是以次日传递为主。
横向上看,以中国为基准市场的CJSP在疫情暴发前后始终高于美股市场,疫情并没有改变A股市场在中美股市的跳跃溢出概率中的主导地位。子样本得出的结论与彭选华(2019)[29]得到的结论相似,他认为沪股具有重要的引导作用,美股的风险溢出有限。但是从全样本看,美股市场更容易引起A股市场发生跳跃现象,中国股市则是处于较为被动的弱势地位。这与李海超等(2020)[30]得到的结论相同,他们指出A股市场的波动具有明显的外生性和输入性的特点,是美股市场冲击的绝对接受者。
从跳的方向上看,利空消息和利好消息对中美股市的冲击程度是截然不同的。尤其,在中国到美国的溢出方向上表现出以下跳为主导的不对称性,这表明源于中国股市的利空消息要比利好消息所引起的跳跃更有可能向美国股市溢出。
2.跳跃溢出强度
选取JSI指标测度三个样本期内中美股市之间的跳跃溢出强度,表5展示了同日和次日的强度值。

表5 跳跃溢出强度(JSI)
纵向上看,蔓延时期的同日JSI较暴发前期明显减弱,次日JSI保持不变,疫情减弱了两国股市在同日引起对方市场发生跳跃的程度,这有可能是疫情蔓延时期两国的金融、贸易联系有所减弱导致的。与CJSP相同,不论是疫情暴发前还是蔓延时,次日JSI更大,表现出一日滞后效应。
横向上看,就同日而言,中美股市对彼此的JSI是一致的;就次日而言,A股市场的JSI略大些。在全样本中,中美股市的同日、次日JSI都处于同一水平。中国股票市场作为新兴市场,却表现出后来者居上,本文认为这受益于金融自由化程度的逐步加深,中国市场对外的影响力日益明显,加深了中美股市跳跃溢出强度不相上下的局面。
与CJSP测度的结果一样,无论是同日还是次日,A股市场对美股市场的跳跃溢出强度存在以下跳为主导的不对称性。美股市场对A股市场的跳跃溢出强度在不受疫情影响时表现得相对平均,在疫情蔓延时表现出以下跳为主导的不对称性。这说明疫情暴发后A股市场受到美股市场负面消息影响的程度更深。
研究认为这与疫情暴发后,美国政府没有及时采取有效的防疫措施,致使疫情在美国不受控制地蔓延,负面消息接踵而至有关。概括地说,美股市场更易受到A股市场利空消息的影响,A股市场在疫情后也表现出相同的不对称性。
3.平均跳跃溢出幅度
选取ASJS指标测度三个样本期内中美股市之间的跳跃溢出幅度,表6展示了同日和次日的幅度值。
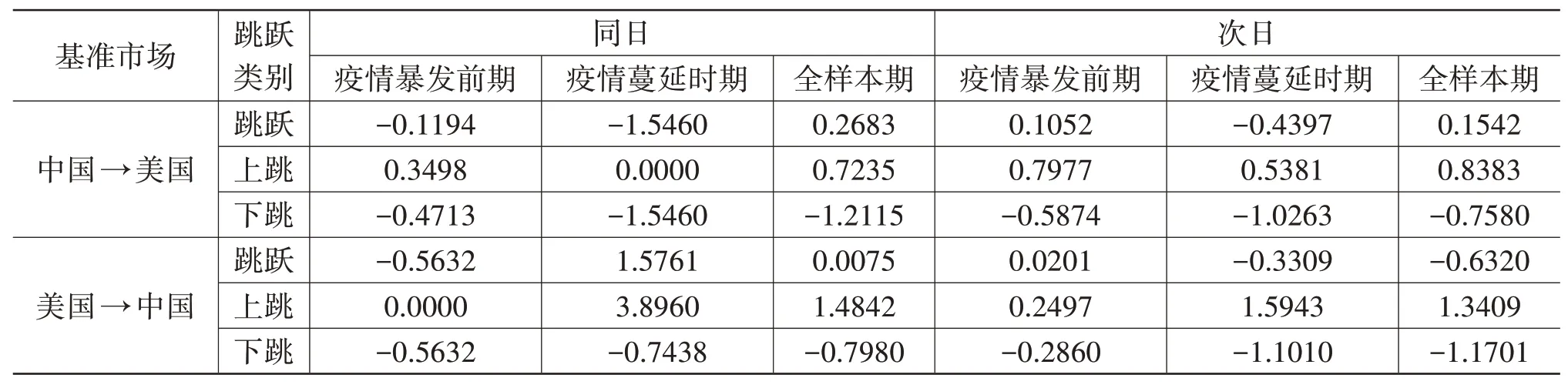
表6 平均跳跃溢出幅度(ASJS)
纵向上看,受到疫情的冲击,A股市场和美股市场的同日和次日ASJS绝对值均有所上升,这表明疫情加剧了跳跃风险在中美股市之间的传染。另外,不论是疫情暴发前还是疫情暴发后,两个市场同日ASJS均高于次日ASJS,信息在当日传播所引起的对方股市跳跃幅度明显大于次日传播所引起的跳跃幅度。这说明信息是具有时效性的,对价格的影响会随着时间逐步衰退。
横向上看,疫情暴发前后都表现为:同日美股市场对A股市场的ASJS更大,次日A股市场对美股市场的ASJS更大。换言之,A股市场的跳跃对美股市场的冲击更缓慢,但美股市场的跳跃对A股市场造成的冲击会更大。这可能是由于美国股市是信息交流的中心,四面八方的消息都会涌入,而来自中国股市的跳跃信息只是这庞大信息池中的一部分,因此被美股市场完全接收到的时间可能出现延迟。中国股市作为新兴市场,很难把精力分散到所有市场,更倾向于关注发达市场的动态,因此对美股市场跳跃信息的反应比较迅速。美国股市已经发展为成熟的国际金融市场,对市场信息的适应力更优,在面对极端风险时,能够很好地处理来自其他市场的信息冲击;而中国股市起步较晚,股票市场的价格调整不及美国股市,受到的冲击会更大。
通过对比上跳和下跳的溢出幅度,发现疫情后A股市场下跳溢出的幅度和美股市场上跳、下跳溢出的幅度均有不同程度的增加,只有A股市场上跳溢出的幅度明显下降。
另外,疫情还改变了美股市场在疫情暴发前ASJS以下跳为主的不对称性,疫情蔓延时ASJS表现为以上跳为主。
(四)跳跃对未来波动的影响
经典的ARCH和GARCH模型设定的前提是每个收益率,无论振幅大小,对其未来波动具有相同的影响,EGARCH、TGARCH和GJR-GARCH等模型是对正负扰动赋予不同的权重来考察收益率对未来波动的影响。这些模型都是将所有幅度的扰动考虑在内,没有区分大小振幅的影响。市场中时常发生的杠杆效应针对的就是大振幅的价格波动(即跳跃),而非一般的价格变化(左浩苗和刘振涛,2011)[31],杠杆效应的存在说明在考察市场扰动对未来波动的影响时有必要区分大小振幅。基于不同扰动分布的GAS模型能够有效地测度跳跃对未来波动的影响,其中基于偏斜t-分布的模型还可以捕捉跳跃杠杆效应。
在表3中,本文验证了新冠肺炎疫情冲击下中美股市存在跳跃情况,接下来将拟合GAS模型来探索这些跳跃对中美股市未来波动的影响。
对上证综指和标普500指数在三个样本期内的日内和隔夜收益率数据拟合ARFIMA-GAS模型,要求at服从广义误差分布、t-分布或偏斜t-分布。拟合的充分性由“混成”统计量Q(10)和Q2(10)来判定。关于ARFIMA(p,d,q)的阶数,借鉴Cheung和Lai(1993)[32]和Kasman等(2009)[33]的做法,让p和q在0≤p+q≤2的范围内变化,由参数估计的显著性、极大似然函数值以及残差诊断等来确定最优的(p,d,q)。
关于at的分布,需要做精确的设定,因为它决定着得分函数st的形式。对于上证综指而言,收益率的γ估计值在三个样本期都是不显著的,故先排除偏斜t-分布;然后,比较对数极大似然函数值,发现广义误差分布的值始终大于t-分布的值,故选择广义误差分布。对于标普500指数而言,无论是日内还是隔夜,γ的估计值都是高度显著的,故偏斜t-分布始终优于另外两种分布。值得一提的是,自由度ν的估计值一直是高度显著的,这意味着at的分布不可能退化为正态分布。
从式(10)—式(12)中的得分函数st可知,若at服从t-分布,则分子分母中包含的冲击(∊t)几乎完全抵消,这表明跳跃对未来波动的影响有限且温和;若at服从广义误差分布,冲击虽有所抵消,但抵消的程度弱得多,这表明跳跃对未来波动的影响是深远的;若at服从偏斜t-分布,则冲击的抵消程度介于t-分布和广义误差分布之间,跳跃对未来波动的影响是适中的,并且具有杠杆效应。表7报告了最优GAS模型的估计及残差诊断结果①因篇幅所限,仅报告了ARFIMA模型的阶数(p,d,q),其他结果可向作者索取。,从中至少可以获得以下几个方面的新发现。
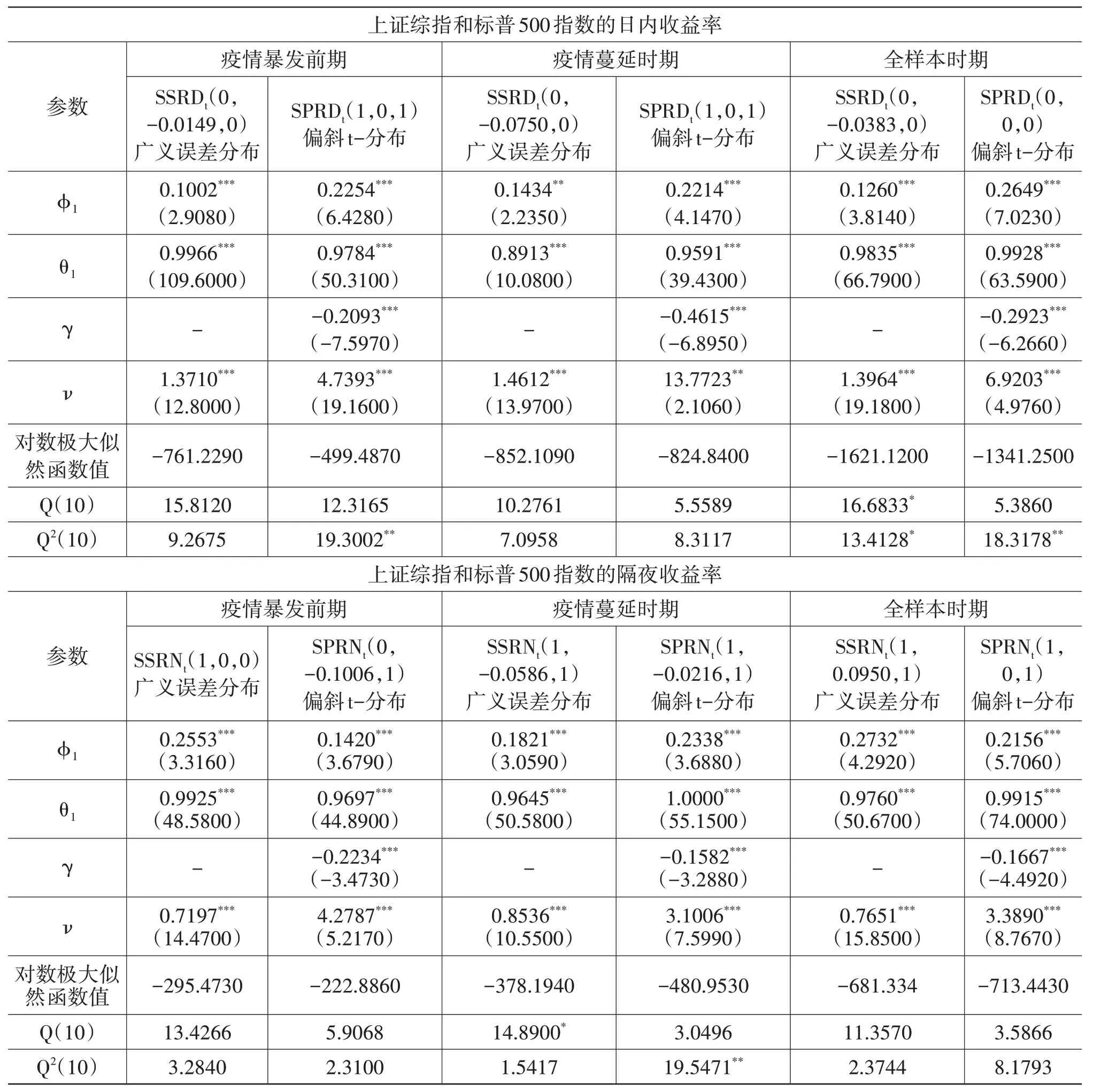
表7 基于广义误差分布和偏斜t-分布的GAS模型估计结果
第一,上证综指在三个样本期都选取广义误差分布,这说明上证综指出现的跳跃行为对其未来波动的影响是深远的,每次跳跃都不可能是一个短暂事件,A股市场很难迅速恢复平静。相比于美股市场,A股市场的有效性较弱,信息在传播过程中易受到阻碍。
第二,标普500指数在三个样本期都选取偏斜t-分布,这说明标普500指数发生的跳跃行为对未来波动的影响是适中的,程度低于上证综指。美股市场是典型的发达市场,全方位发展已经相对成熟。对比A股市场,它是强有效的,因此信息能够在市场中较快传播并且很快被消化掉。
第三,根据表7中γ值,可以发现美国股市无论在白天交易时段还是夜晚闭市时段都存在跳跃杠杆效应;而中国股市恰恰相反,在任何时段都不存在跳跃杠杆效应。这巩固了前人的共识,即普遍认为欧美发达市场均存在杠杆效应,而像中国、巴西等新兴市场通常不存在杠杆效应。
第四,疫情暴发前后对分布的选择是一致的,这说明不管是美股市场还是A股市场,跳跃对其未来波动的影响以及跳跃杠杆效应在新冠肺炎疫情暴发前后没有发生显著性变化。
总之,跳跃对中美股市未来波动的影响是客观存在的,而且有很大差异,但是新冠肺炎疫情没有改变各自的影响程度。
五、结论与建议
本文基于SVCJ模型测度了疫情暴发前后中美股市之间的跳跃溢出概率、强度及幅度,并运用GAS模型分析了疫情暴发前后中美股市的跳跃对各自未来波动的影响,获得了一些结论。
第一,中美股市在疫情暴发前后均存在明显的跳跃成分,且利空消息比利好消息更容易引起股市的跳跃溢出。
第二,中国股市对美国股市的影响力逐渐增强,子样本中中国股市对美国股市的跳跃溢出概率更高、强度更大,在两国股市跳跃溢出效应中起主导作用。
第三,中美股市的跳跃溢出概率和强度都存在一日滞后效应。
第四,跳跃的发生对中美两市未来波动的影响是客观存在的,而且疫情并未改变这种影响程度,但是中国股市的跳跃对其未来波动的影响更加深远;美国股市在白天和夜间均存在跳跃杠杆效应,而中国股市不存在跳跃杠杆效应。
在这些结论中,有的巩固了前人的成果,有的是本文的新发现。
根据以上结论,本文提出以下建议。
一是投资者应该把更多的注意力放在中国股市,不要过度受到美国股市变动的影响。尤其是在发生新冠肺炎疫情之类公共卫生突发事件时,中美两国抗击力度不同导致两国的经济环境也大不相同,此时更应着眼于本国制定恰当的投资组合,排解美国股市负面消息造成的恐慌。
二是金融监管机构应该提高信息处理的效率,利用一日滞后的时间差,在下一个交易日到来之前尽可能地降低外部冲击。
三是政府应该加速推动经济内循环形成,降低对国外供给和需求的依赖性,进而提高对国际公共卫生突发事件的抵御能力。
