月度自然利率的估计及应用：Phillips曲线的影响

张舒媛，郇志坚，卢爱珍，周思齐

（1.新疆财经大学金融学院，新疆乌鲁木齐 830000；2.中国人民银行乌鲁木齐中心支行，新疆乌鲁木齐 830000）

一、引言

当前国际环境日趋复杂，世界正经历百年未有之大变局，我国经济发展面临需求收缩、供给冲击、预期转弱三重压力，外部环境更趋复杂和不确定，我国经济遭遇的宏观随机冲击的频率和幅度也不断增加。在此背景下，2021年12月召开的中央经济工作会议指出，稳健的货币政策要灵活适度，保持流动性合理充裕。加大宏观政策跨周期调节力度，提高宏观调控的前瞻性针对性。

利率对宏观经济的均衡和资源配置方面有着重要的导向意义。目前，我国已形成较为完整的市场化利率体系，该体系运用货币政策工具调节银行体系流动性，释放政策利率调控信号，引导市场基准利率以政策利率为中枢运行，并通过银行体系传导至贷款利率，调节和优化资源配置，实现货币政策目标（易纲，2021）[1]。

自然利率是与经济长期潜在产出和稳定的通货膨胀（以下简称“通胀”）相符的短期实际（经通胀调整后）利率（Yellen，2015）[2]，能够影响市场基准利率水平。同时，自然利率与市场基准利率的差值能够衡量货币政策调控的“松”“紧”程度，对能否精准实现货币政策最终目标至关重要，因此自然利率也被视为货币政策的“锚”。目前，纽约联邦储备银行（以下简称“纽联储”）基于季度数据估计美国自然利率并将估计结果作为货币政策调控的依据之一，其采用的估计方法测度精度相对较高但时效性较差，难以满足当下各国对货币政策调控的更高要求（Kiley，2020）[3]。

综上，将自然利率作为货币政策调控的依据有助于提高货币政策调控的精确性，而进一步实现自然利率的月度估计，并充分考虑通胀的动态因素，既能提高估计的频率和精度，又有助于提高货币政策调控的灵活性、准确性和稳健性。

实践中，各国央行可以基于市场基准利率与自然利率的差值变化来引导货币政策调控，但这受限于通胀水平是否合理和Phillips曲线是否有效。通胀是决定自然利率的重要因素之一，也是央行调控货币政策的重要指标，在LW—HLW模型中，Phillips曲线把产出缺口和通胀联系起来，并主要从两个途径影响自然利率的估计结果。

一是通过调整Phillips曲线的设定影响产出缺口，进而影响自然利率。已有研究论证了季度Phillips曲线的指标选取（Laubach和Williams，2003；徐忠和贾彦东，2019）[4-5]、参数设定（Lopez-Salido等，2020）[6]等会影响自然利率的估计结果，而本文构建的月度Phillips曲线较原季度模型设定更为复杂，有理由认为月度Phillips曲线设定的调整也可能引起自然利率估计结果的波动。

二是通过通胀预期影响事前实际利率，进而影响自然利率。通胀受其预期影响已基本达成学界共识（Lucas，1972；Blanchard等，2015）[7-8]，而在自然利率估计中，事前实际利率这一指标是名义利率与通胀预期的差值，因此通胀预期的变化将影响事前利率水平，从而影响估计结果。

首先，实现自然利率的月度估计，根据估计结果判断月度Phillips曲线是否有效，并初步分析我国货币政策的调控效果。

其次，借鉴Lopez-Salido等（2020）[6]的策略，分析月度Phillips曲线滞后设定和预期跨度如何影响自然利率估计结果，并检验估计结果的稳健性。

再次，总结梳理相关重要结论。

本文其他部分安排为：第二部分整理并分析与自然利率估计相关的主要研究；第三部分介绍LW—HLW模型，详细分析自然利率估计的主要方法和相关原理；第四部分和第五部分为实证分析，第一步得到月度自然利率的估计结果，第二步对比不同Phillips曲线设定下的不同估计结果；第六部分是主要结论和研究展望。

二、文献综述

Wicksell（1898）[9]最早提出了自然利率的理论思想。Myrdal（1939）[10]进一步提出，自然利率是与资本收益率或生产率相符，使储蓄与投资相等并保持物价中性的利率。理论上，自然利率是宏观经济总供求达到均衡时的实际利率水平；实践中，利率的高低直接影响老百姓的储蓄和消费、企业的投融资决策、进出口和国际收支，进而对整个经济活动产生广泛影响（易纲，2021）[1]。

（一）自然利率的混频估计

自然利率不能被直接观测，大部分研究以提高估计准确性为主，多侧重于估算方法的多样性，而关于混频自然利率的估计则较少。本部分重点梳理自然利率的主要估算方法以及自然利率混频估计的相关原理。

1.自然利率的主要估算方法

基于经济学模型的自然利率估算方法主要有半结构模型、结构向量自回归模型、时变向量自回归模型、动态随机一般均衡模型（DSGE）等。其中，半结构模型的设定虽然简单，但适用性和可比性较强，因此也最为常用。该模型的理论框架源于新凯恩斯理论下的简约总供求均衡模型，具有坚实的经济学理论。在此基础上，通过纳入状态空间模型，再利用多变量的卡尔曼滤波（Kalman Filter）方法实现自然利率的估计。随着该方法不断发展，形成了估计自然利率的经典Laubach和Williams模型（2003）[4]，以及Holston等模型（2017）[11]。

经典的LW—HLW模型结合新维克赛尔理论框架（Woodford，2003）[12]与均衡利率的定义，通过构建包含产出、利率和通胀等变量的经济动态模型，利用卡尔曼滤波进行联合估计，同时得到自然利率、潜在产出缺口等相关变量。近年有学者尝试在原模型基础上加入其他影响因素，提高估算精确性，但是Laubach和Williams（2016）[13]认为，现有原模型可以实现多个不可观测变量的联合估计，估计结果较为简洁和稳健，也符合实际，具有较强的优势。如果需要加入其他影响因素来改善模型，建议可以将这些因素以类似于索洛余量的形式纳入原模型的时间偏好中。

2.混频估计的主要原理

传统模型只能对相同频率的变量进行回归。采用状态空间方法时，需要将低频数据处理为具有缺失值的高频数据，再将其作为状态变量，运用卡尔曼滤波进行估计，从而实现混频估计。对于流量数据，通过低频数据时期聚合（Temporal Aggregation）关系转化为线性约束。而对数的流量数据则为复杂的非线性约束，处理该部分数据可使用扩展卡尔曼滤波（Extended Kalman Filter，EKF）将混频非线性约束转为线性化约束。EKF的主要原理是通过截断非线性函数的泰勒展开式，略去非线性观测方程和状态方程泰勒展开式中的2阶及以上项，从而实现非线性函数的线性化。

3.我国自然利率的估计

我国学者运用不同的估算方法、选取不同的利率指标、在不同的模型设定下估计了我国的自然利率，目前估计结果均为季频且存在一定差异。潘淑娟和叶斌（2013）[14]使用三个月上海银行间同业拆放利率（SHIBOR）估计我国自然利率水平，得到的估计结果在0附近波动。李宏瑾等（2016）[15]、李宏瑾和苏乃芳（2016）[16]将人口和货币政策作为其他影响因素纳入了LW模型，得到的自然利率估计结果均值为2.5%。徐忠和贾彦东（2019）[5]则使用三种不同模型分别估计我国的自然利率，并将三组估计结果进行平滑处理，得出的估计结果均值约为0.3%。

目前，国内学者主要围绕季频估计展开研究，这对于日度的利率数据而言时效性相对不足。同时，虽然学界普遍认可通货膨胀对自然利率的影响，但鲜有学者考虑Phillips曲线的不同设定对估计结果的影响。由此，将混频估计和自然利率估计的方法相结合，并考虑不同Phillips曲线的设定可能会对估计结果产生的影响，有助于提高估算的及时性和准确性，从而为更加精确、灵活地调控货币政策提供依据。

（二）Phillips曲线

Phillips曲线为总需求与总供给模型提供了一个简单的解释，重点揭示了经济增长率与物价上涨率这两者之间的关系。Phillips（1958）[17]提出Phillips曲线用于证明通胀率与失业率之间的关系。之后，经济学家进一步用经济增长率指标替代失业率指标，Lucas（1972）[7]提出“产出—物价”Phillips曲线，分析通胀与产出之间的关系，使其成为宏观经济研究的重要因素和货币政策调控的重要依据。Phillips曲线是LW—HLW模型重要的构成部分，因其结构复杂，影响因素较多，对自然利率估计结果产生的影响较大。随着Phillips曲线理论的完善、对各国宏观经济刻画精度的提升，不同设定对提高自然利率估计结果的精度具有重大影响。

1.Phillips曲线研究的拓展

相关研究从诸多方面得到扩展，本文后续估算主要涉及滞后结构和预期跨度两个方面。

一是引入滞后项。Fuhrer和Moore（1995）[18]指出，通胀具有持久性，因此当前值与滞后值之间存在较高相关性。Gali和Gertler（1999）[19]将滞后通胀重新引入新凯恩斯Phillips曲线并得出混合型新凯恩斯Phillips曲线。Rudd和Whelan（2005，2006）[20-21]通过实证发现引入滞后通胀能较好拟合通胀动态过程。齐鹰飞（2011）[22]运用实证方法论证了中国的通胀与其滞后值之间存在显著相关关系。

二是引入预期。通货膨胀受其预期影响的思想至少可追溯到Phelps（1967）[23]和Friedman（1966）[24]，研究者通过引入适应性预期构造出附加预期的Phillips曲线，开创了现代短期通胀动态研究。Cogley和Sbordone（2008）[25]推导出包含趋势通胀变动以及高阶通胀预期的新凯恩斯Phillips曲线的变形形式。Scheibe和Vines（2005）[26]实证检验我国数据，认为通胀预期是我国通胀的重要影响因素。

2.LW—HLW模型下的Phillips曲线相关研究

主要从模型构建、指标选取等方面考察Phillips曲线对自然利率估计的影响。模型构建方面，Lopez-Salido等（2020）[6]基于季度HLW模型，分别运用通胀和前瞻性通胀开展估计，对比模型参数和估计结果的差异，并分析产生差异的原因。指标选取方面，为准确描述宏观经济运行特征，LW模型在Phillips曲线中加入进出口和石油价格；我国学者尝试加入汇率、房地产价格等因素估计自然利率，但是估计结果出现较大差异（徐忠和贾彦东；2019；邓创等，

2012）[5，27]。

此外，Lopez-Salido等（2020）[6]还对比了运用CPI和PCE作为通胀指标的估计结果，由于两组估计结果较为接近，研究者认为其对自然利率估计的影响较小。

3.我国Phillips曲线的相关研究

我国的宏观调控越来越关注通胀，涉及Phillips曲线的研究主要集中于以下两方面。

一方面是通过实证验证Phillips曲线在我国宏观经济运用中的可行性。

另一方面则是运用Phillips曲线分析产出缺口对我国通胀的影响。

刘金全等（2006）[28]运用具有区制转移的状态空间模型验证经济增长率与通胀的关系后，认为我国的“产出—价格”特征符合长期Phillips曲线的性质，一定程度上证明Phillips曲线的重要性。杨小军（2011）[29]构建了附加利率的Phillips曲线，通过相关实证分析得出利率是通胀的主要驱动因素的结论。通胀的动态变化受到惯性和预期的共同影响，且后者作用更大。

（三）文献述评

在估算方法方面，我国自然利率的月度估算更适用状态空间方法。在混频估计方面，目前将混频估计与自然利率估计相结合的研究相对较少。由于混频数据包含更全面的信息，运用混频数据开展估计通常可以获得更精准的估计结果，因此有必要考虑将混频数据与我国自然利率估计相结合，研究混频数据下自然利率的估计值和特征，提高观测频率。在模型设定方面，准确理解通胀的动态过程有助于更好地调控货币政策，所以有必要考虑Phillips曲线的设定和预期对估计结果的影响。同时，目前对月度Phillips曲线的研究较少，其设定是否会影响月度模型的稳健性，也具有一定的考察价值。

综上所述，考虑到混频估计方法能使数据可利用的信息更全面，估计结果更具时效性，本文将季度GDP、月度通胀和日度利率数据相结合，将混频估计方法与自然利率估计的半结构模型相结合，采用状态空间方法估计我国月度自然利率，并重点从滞后结构和预期两个因素分析月度Phillips曲线设置对估计结果的影响。

三、LW—HLW混频估算模型的简要介绍

（一）模型的介绍

季度LW—HLW模型在新凯恩斯框架下，联立IS曲线和Phillips曲线方程，将其设置为观测方程，通过设置相对应的状态方程进行联合估计，以此估算其在均衡状态下的经济增长率、产出缺口和自然利率。详细内容参见Laubach和Williams（2003）[4]以及Holston等（2017）[11]的文献，在此不做赘述。

在此基础上，本文将原来的季度估计频率提高至月度估计频率，由此得到简化后的月度IS曲线如式（1）：

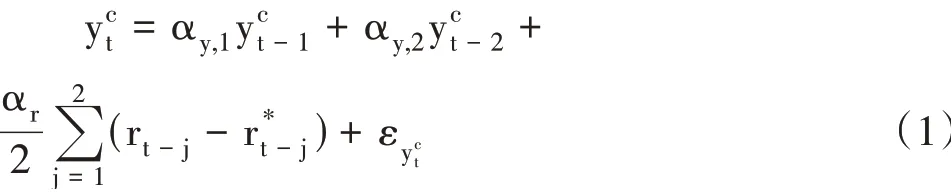
rt是事前实际利率，详细的计算公式如下：

式（2）中it是无风险单期名义利率是通胀的预期值，εyc

t是产出缺口的冲击。

国内外对于Phillips曲线滞后阶数的设定没有统一的标准，为充分捕捉月度通胀序列的动态调整机制，在这里参考O’Reilly和Whelan（2005）[30]提出的广义Phillips曲线形式构建式（3）中的广义Phillips曲线：

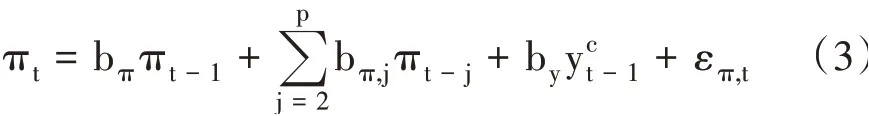
式中πt表示通胀率，πt-j是j阶滞后，bπ,j为回归系数，p为通胀率滞后阶数，επ,t为捕捉通胀的短暂冲击。

进一步分析滞后阶数p的选取，在现有的相关研究中，较为通用和规范的选取方法是通过比较AIC和SBC等信息准则来选取p。

现有的低频估计中，Scheibe和Vines（2005）[26]，Holston等（2017）[11]均认为p应为1年，也就是12个月。而实践过程中，滞后阶数p与模型的拟合优度和对数似然函数值之间具有较强的正向关系。因此，结合滞后阶数对当期通胀率产生影响的有限性和模型的简洁性，此处不固定p，而是以AIC信息准则作为指标的方式筛选确定p。仅约束p≤12，设置2至p阶滞后项系数相同，则月度Phillips曲线如式（4）：

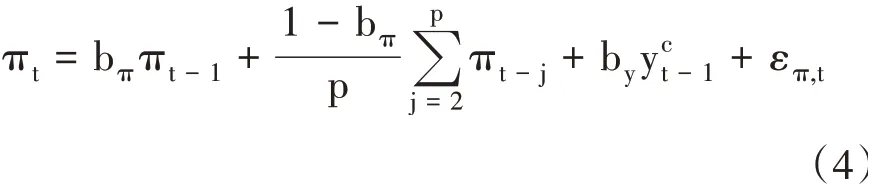
以自然利率与产出增长之间的理论联系为基础，假设得到：

其中，gt是自然产出的趋势增长率，zt则为影响的其他因素。原模型中的产出增长率的估计系数接近于1，后续纽联储在实际应用过程中也将其设定为1，故综合我国实际和国际经验，本文同样将系数设置为1。

预先对拆分后的月度产出做季节调整，对季调后的数据进行检验，结果显示其服从I（2）的过程。因此，此处将产出设定为I（2）过程以避免估计实际GDP增长的无条件均值。设定潜在产出为具有漂移项gt的随机游走（Random Walk）过程，其中漂移项gt本身也符合随机游走过程，如式（6）和式（7）：

参照纽联储设定，考察zt服从随机游走过程，如式（8）：

本文假设εy*,t、εg,t和εz,t是分别具有标准差σy.*、σg和σz的正态分布，且序列和同期之间不相关，所有方程中的残差都服从正态分布。

（二）混频处理

使用状态空间方法进行混频处理时，要先构建高低频数据桥接关系式，将低频数据视为具有缺失值的高频数据后，再进行处理。对于流量数据，如GDP须满足时期聚合的线性约束，即季度内各月GDP之和等于季度GDP。经济分析中GDP多采用对数形式，其约束为较为复杂的对数非线性约束，主要通过对非线性函数的泰勒展开式进行1阶截断，经过数次迭代后实现线性化。

本文在LW—HLW模型框架下，使用扩展卡尔曼滤波将高低频非线性的对数约束线性化，也就是使用扩展EKF将季度GDP与月度GDP这两类不同的高低频数据的对数非线性约束进行线性展开后，得到最终的月度对数GDP，如式（9）：

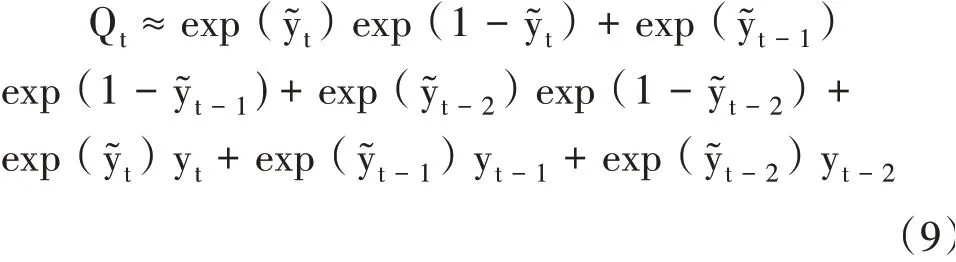
（三）估算方法

基于EKF的混频GDP对数线性化展开与LW—HLW模型相结合时，模型本身的复杂度会使迭代计算负担过重，故此处选择先拆分季度数据，再开展估算。

在此处使用的状态空间方程中，观测方程为式（1）和式（4），状态方程为式（6）至式（8）。估计的具体步骤如下：

首先，使用EKF拆分季度GDP数据为月度

GDP；

其次，将拆分后得到的月度GDP对数作为观测变量，整合至LW—HLW模型的状态空间方程中；

再次，使用中值无偏估计和SKF估计得到相应的自然利率估计值。

趋势增长率与自然利率的波动对于数据整体波动的贡献相对较小，使用最大似然法进行参数估计时会导致zt和gt的冲击方差为0。因此，本文使用中值无偏和极大似然估计相结合的参数估计方法。其中的两个比率分别为和使用这两个比率并采用最大似然估计得出模型的剩余参数（包括σy*和σyct）。

所有计算均由经济计量软件WinRATS 10完成。由于样本时间序列较短，为充分挖掘样本信息，最终使用全样本的平滑估计进行分析。同时，考虑到状态向量包含单位根，所以样本前数据采用遍历设定，估计算法采用BFGS算法。

四、实证分析

（一）数据处理

实证分析所需要用到的数据中，季度GDP和月度CPI数据均来自我国国家统计局的官网，利率数据则来自Wind数据库。由于2019年12月后的新冠病毒感染为重大突发事件，纽联储在这之后对自然利率估计的模型进行了调整，同样为避免该影响，本文将估计区间设定在2007年1月至2019年12月。与此同时，按照原LW—HLW模型的数据处理流程，对三组数据进行预处理后纳入混频估计模型进行估计。具体预处理如下。

名义利率。根据我国利率市场现状和半结构模型的相关研究（张舒媛等，2020）[31]，选择SHIBOR隔夜拆放利率作为名义利率指标。由于利率数据的频率为日度，故首先把每月内的所有日度SHIBOR隔夜拆放利率加总，其次将加总后的数据取算术平均得到月度SHIBOR，再次将其进行年化处理后可得到相应的月度名义利率，即it=100*((1+SHIBORt/36000)365-1)。

实际季度GDP。由于我国未发布实际季度GDP，本文在此处对GDP数据的处理方式为：首先，选取目前已公布的所有当季现价GDP数据，使用年度平均指数平减得到2000年不变价的季度GDP；其次，使用Denton法与年度实际GDP进行衔接；再次，对其进行X13季节调整，对结果取对数后做年化处理，即yt=400*log(RGDP)。

通胀率。我国国家统计局未发布PCE数据，因此选取CPI作为衡量通胀的指标。我国国家统计局自1987年1月开始发布当月同比CPI，1995年1月发布当月环比CPI，为统一数据口径。首先，将1995年1月前的CPI进行月度同比转换得到环比的数据；其次，在此基础上以2006年6月定基100，计算定基环比序列，年度定基CPI序列进行Denton衔接调整（张舒媛等，2021）[32]；再次，同样使用X13进行季节调整，取对数差分并年化处理，得到通胀率πt，即πt=1200*log(CPIt/CPIt-1)。

通胀率预期。月度LW—HLW模型中包含事前实际利率这一指标，该指标需从名义利率中剔除通胀的影响。为便于估计，假定通胀率动态滞后2≤p阶的系数均相同，以一季度、半年、一整年为例，简化分析通胀率受过去2个月、5个月、11个月的影响，即AR（2）、AR（5）、AR（11）。本文选取通胀率数据滚动窗口的提前年限为n，最大跨度为10年，即使用前120个月数据计算通胀预期。

（二）混频估计结果

由于LW—HLW模型不稳定，本文使用的无偏中值估计法共分为三个阶段：第一个阶段估计参数λg，第二个阶段估计参数λz，第三个阶段则使用极大似然法估计剩余参数。本文仅给出最后阶段的最终估计结果（见表1）。

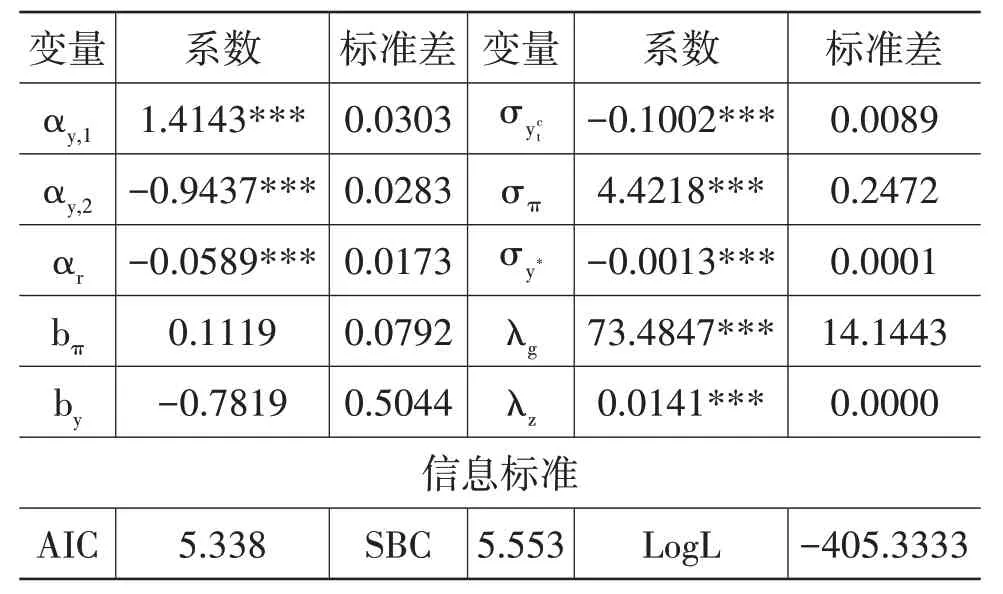
表1 我国月度自然利率估计的模型参数

产出缺口方程中，产出缺口及其滞后项的系数αy,1、αy,2之和小于1且显著性水平均小于1%，符合稳定性条件。同时分别作为周期、通胀率、产出缺口的冲击方差，标准差的波动大小在一定程度上可以反映模型的估计效果。

我国月度自然利率估计结果见图1。整个样本区间内的自然利率估计结果整体呈下降趋势，其中，2008年10月受金融危机影响，为历史最低值1.06%；2019年12月自然利率处较低水平，为1.17%，仅高于金融危机时期。

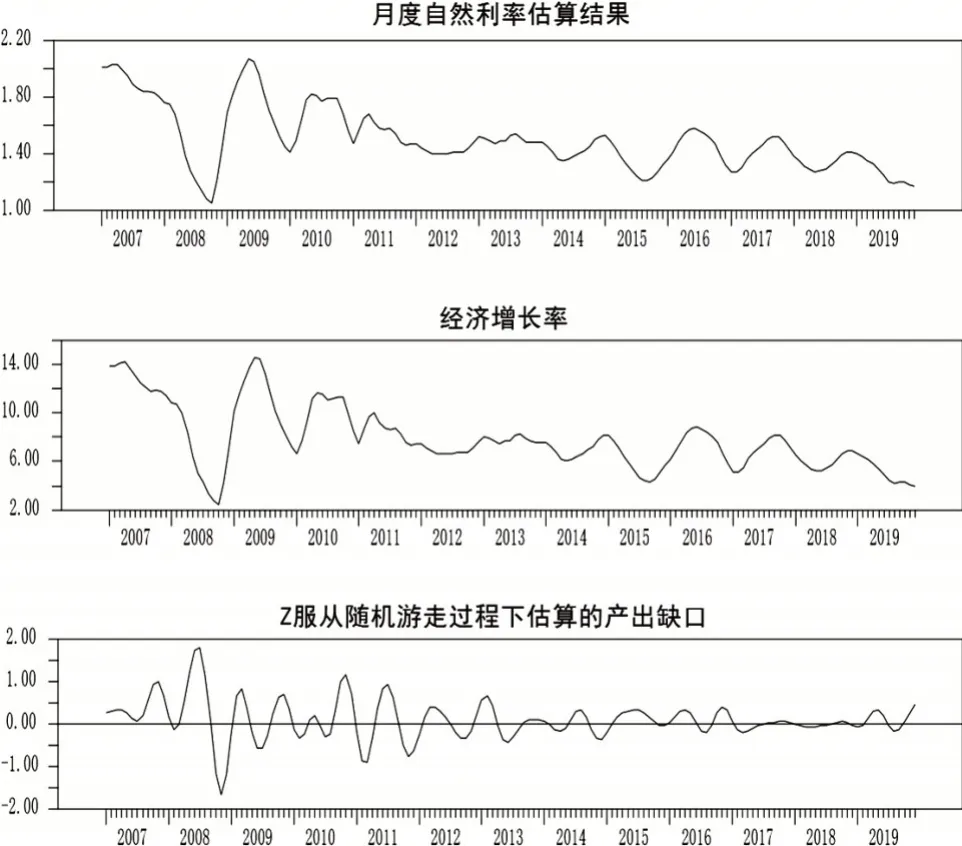
图1 我国月度自然利率估计的时序图

2008年，中国人民银行于9月至11月多次下调存贷款基准利率。12月，自然利率回升至1.44%，SHIBOR隔夜拆放利率降至自然利率下方，进入适度宽松状态，避免了可能出现的经济剧烈下行，在一定程度上有效促进了金融市场稳定和经济社会发展。

在整个样本区间内，2008年12月至2014年12月的自然利率估计值维持在1.21%—2.07%。在2008年11月发布的进一步扩大内需、促进经济增长等宏观经济政策的刺激下，经济增速快速回升至10%左右。随后，企业和地方部门债务率增高，中国人民银行适度调整货币政策，SHIBOR隔夜拆放利率保持在自然利率上方，有效落实了当时中央经济工作会议提出实施稳健货币政策的要求。

2015年1月至2019年12月，这一阶段自然利率处于历史较低水平。自然利率估计值波动幅度较为规律，波动区间为1.17%—1.59%，但整体仍呈现下行趋势，这与诸多学者判断基本一致。其间，2015年3月人民银行下调金融机构人民币存贷款基准利率，同时推进利率市场化改革，扩大金融机构存款利率浮动区间上限。经过1个月的时间，SHIBOR隔夜拆放利率与自然利率的差值有效收窄至0.9个百分点。

2015年5月，综合考虑融资成本、需求层面导致的通胀预期下行风险，中国人民银行宣布降息25BP，精准引导SHIBOR隔夜拆放利率降至自然利率下方，并将二者差值控制在1.2个百分点左右，为量化宽松留有空间。2015年7月，李克强总理在经济形势专家和企业负责人座谈会上指出要实施稳健的货币政策，SHIBOR隔夜拆放利率于同月再次小幅回升至自然利率上方，二者差值保持在1.4个百分点以内，实现了调控时机和调控力度“双精准”，高效服务实体经济。

五、Phillips曲线滞后与预期的影响

估计自然利率的另一个难点在于模型本身的稳健性普遍不足，不仅仅是模型整体的不同设置，参数设定和个别指标的轻微变动都可能导致估算结果的大幅波动（Laubach和Williams，2016；He等，2015）[13,33]。而Phillips曲线的滞后会影响模型设置，其预期则影响实际事前利率这一指标，因此二者均可能影响模型的稳健性。

从模型设定看，滞后期不同时，式（3）Phillips曲线方程中的πt-j将影响产出缺口的估计；预期不同时，式（2）的和rt将会不同。由此可见，Phillips曲线的滞后期不同和预期不同均会影响r*t的估计结果。

（一）包含通胀滞后因素的估计结果

Fuhrer和Moore（1995）[18]、Gali和Gertler（2001）[34]、Christiano等（1999）[35]、Cogley和Sbordone（2008）[25]等充分考虑滞后因素的影响，分别基于不同假设，推导出包含内在持久性的Phillips曲线，论证了Phillips曲线滞后阶对自然利率估计结果的影响。

目前，国内外尚未形成关于月度Phillips曲线的成熟理论，同时考虑到预处理时对通胀率进行了平滑处理，本文分别估计滞后1个月至2年的月度自然利率。在估算过程中，为兼顾模型简洁性，模型仅估算1阶系数并令2阶至n阶系数相等，以滞后一季度为例，阶数取3且令2—3阶的系数相等。

表2为三组具有代表性的估计结果，对应的滞后期分别为一季度、半年、一年。各组估计结果的系数相似，产出缺口及其滞后项的系数αy,1、αy,2之和均小于1，且显著性水平均小于1%，符合稳定性条件，认为模型较稳定。

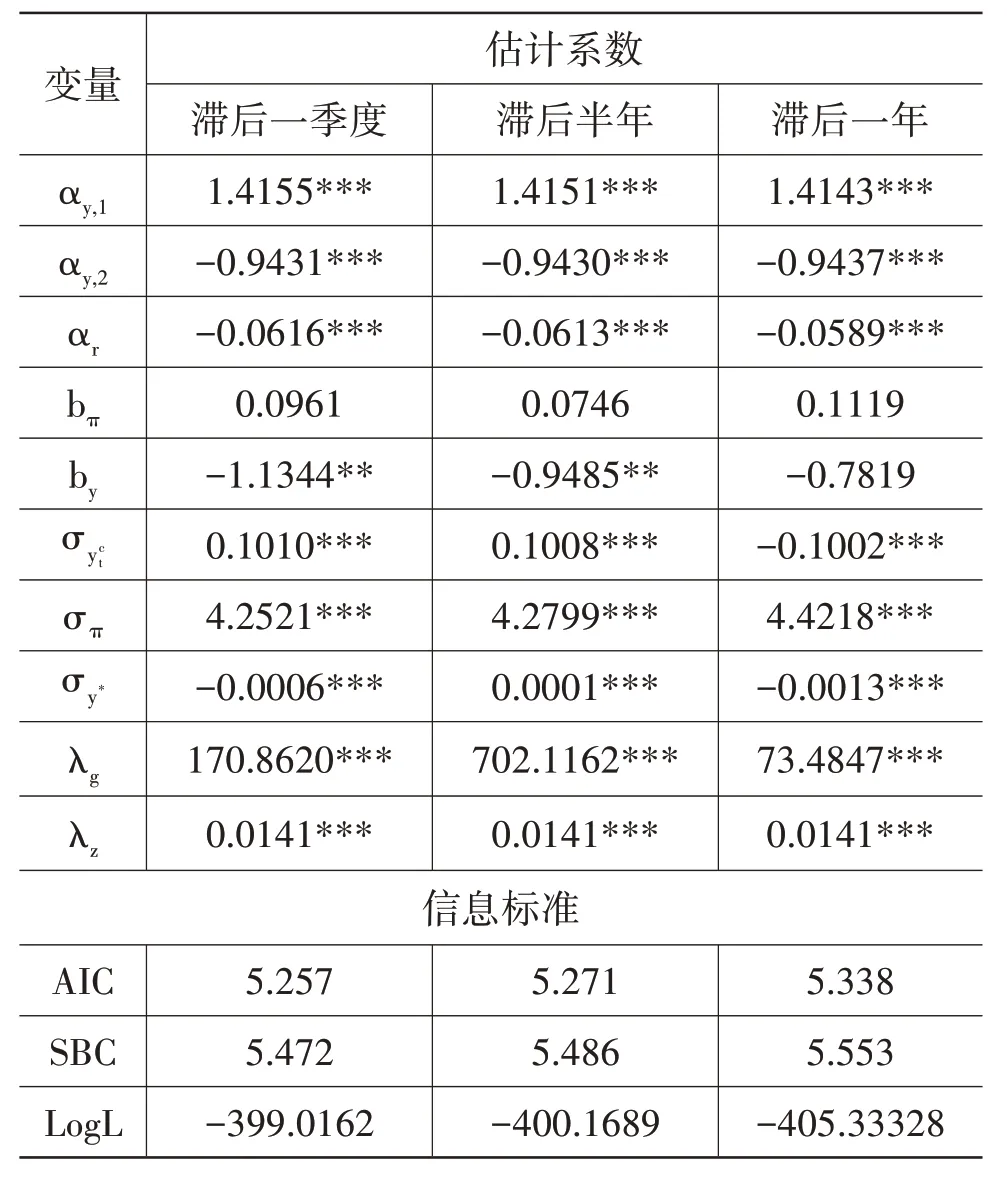
表2 通胀滞后一季度、半年、一年时月度自然利率估计的模型参数

总体上来看，在Phillips曲线不同滞后阶数的设定下，模型估计的参数差异较小，模型也较为稳定。相较而言，滞后半年以上的模型估计效果相对略优。滞后半年以上时，Phillips曲线较陡峭，对实际利率缺口αr的变化弹性也更高，更为敏感。滞后一年时，缺口略大，反映了通胀的持续性有所增加；显著且小幅的下降，反映了潜在产出增长率的影响有所减弱。

Phillips曲线的通胀率分别滞后一季度、半年、一年时，月度自然利率估计结果如图2。三组自然利率走势高度相似，但滞后一年时，自然利率对外部冲击更为敏感，波动略大。滞后一季度和半年时，自然利率较为接近且相对偏低，分别为0.40%—1.39%和0.35%—1.35%。结合已有研究，本文认为滞后一年时的估计结果更符合我国实际。

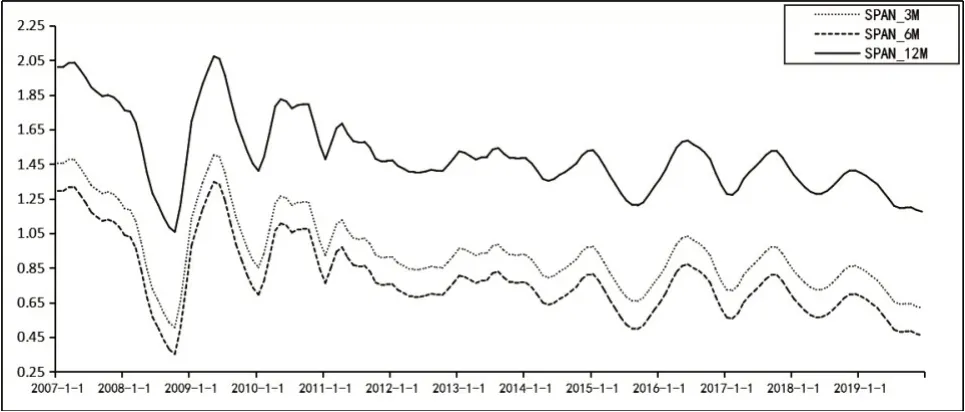
图2 通胀滞后一季度、半年、一年时月度自然利率的估计结果

（二）包含通胀预期因素的估计结果

预期理论说明了预期对通胀的重要作用（Carlson和Parkin，1975）[36]。事前实际利率是名义利率与通胀率预期之差，因此通胀率预期的调整，将直接影响自然利率的估计结果。Coibion和Gorodnichenko（2013）[37]提出，滚动窗口估计和递归估计适用于系数随时间变化可能存在结构性变化的情形。其中，滚动窗口既能够实现预测，又克服了已经实现的预期值会随信息更新而变化的不足（何启志和姚梦雨，2017）[38]。

因此，本文首先选取提前5—10年的数据滚动窗口，其次结合上文，将Phillips曲线的通胀率设置为滞后1年，再次分析不同通胀率预期对估计结果的影响。

通胀预期为5—10年时月度自然利率估计的主要参数输出结果如表3所示。不同通胀预期下，各组估计系数也高度相似，产出缺口及其滞后项系数αy,1与αy,2之和小于1且显著性水平同样小于1%，这符合稳定性条件，因此可以将其视为较稳定的估计模型。

表3 通胀预期为5—10年时月度自然利率估计的模型参数

当滚动窗口分别提前5年、6年、10年时，估计的产出缺口对利率波动较为敏感。提前7年、9年、10年时，估计结果较大，反映通胀的持续性有所提高。提前6年、7年、10年时，by均增加，Phillips曲线变得更陡峭。此外，各组结果中λz均未发生变化，而波动较大，反映潜在产出的趋势增长率对自然利率的冲击较大。

进一步分析月度自然利率的估计结果（如图3），在不同通胀预期下，各组估计结果表现稳健，波动趋势高度相似，估计值均在0.94%—2.63%之间。除通胀预期为5年时的自然利率估计结果略大外，其他组的估计结果均略低于原模型。结合主要参数的表现和已有研究，本文认为滚动窗口提前10年估计效果最佳。

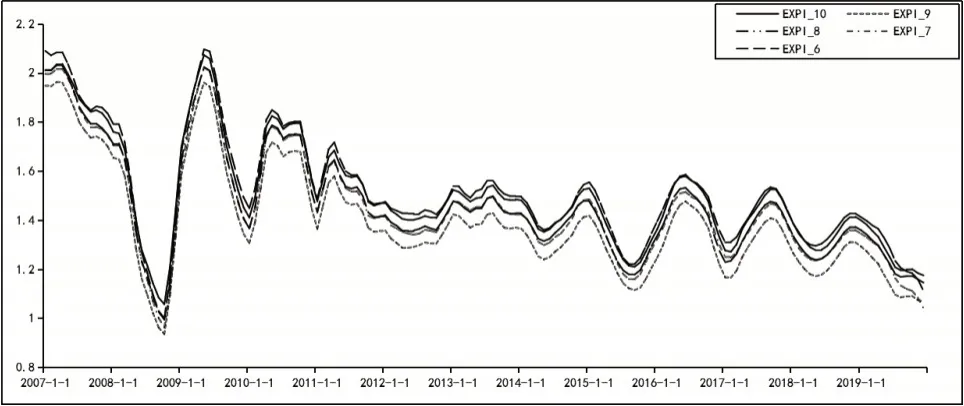
图3 通胀预期为5—10年时月度自然利率的估计结果

综上所述，自然利率估计模型中，Phillips曲线将通胀率滞后期设置为一年即12个月、将通胀率预期的数据滚动窗口提前10年时，模型的估计结果较好。此时，通胀对自然利率的影响较为明显，这与现实情况更为接近。同时，在此设定下估计得到的自然利率能够精确刻画我国不同时期的主要经济特征。结合现实和理论分析得到，产出缺口对利率波动更为敏感，潜在产出的趋势增长率对自然利率产生的影响较为明显。

从模型稳健性方面来看，虽然Phillips曲线的滞后期和预期设定有所不同，但各组模型估计的系数接近，自然利率的估计结果走势高度一致且保持在合理区间波动，证明了混频自然利率在及时捕捉经济波动的同时，也保持了较好的稳健性。

六、结论与展望

（一）主要结论

首先，本文在季度LW—HLW模型的基础上，结合我国实际情况和相应的数据特征，构建了半结构化模型。

其次，运用EKF将季度GDP拆分为月度GDP，对各组指标进行预处理后得到月度GDP的对数、月度名义利率以及月度通胀率数据。数据的预处理完成后，再使用中值无偏方法进行联合估计，得到各不可观测变量的估计值并实现我国自然利率的月度估计。

再次，针对我国宏观经济特征，进一步考虑了通胀动态特征对货币政策的影响，从Phillips曲线的滞后和预期两方面分别考察其对自然利率估计结果的影响，同时检验了模型的稳健性。

在估算方法的使用方面，本文使用扩展卡尔曼滤波不仅解决了混频数据的约束关系非线性问题，还实现了LW—HLW模型与混频线性展开的整合。模型的估算结果显示，加入混频技术后，我国自然利率测度的频率得到了有效提升，不仅得到了样本区间内的各月度自然利率估计结果，而且能清楚获得其动态的变化过程，及时反映了货币政策调控的效果。

Phillips曲线作用方面。

一是调整月度Phillips曲线的设置未对估计参数产生较大影响。该结果在验证模型稳健性的同时，也印证了近年Phillips曲线在实践中效力有所弱化的实际。相较而言，Phillips曲线的滞后期为半年及半年以上时，产出缺口对利率波动更为敏感；Phillips曲线的预期设置为7年、8年、10年时，自然利率对产出的趋势增长率波动更敏感。

二是调整月度Phillips曲线的设置未对自然利率估计结果产生较大影响。所有估计结果均在2009年以来呈现下降趋势，且估计结果保持在0.35%—2.63%之间。相较而言，通胀滞后期较短或预期时间较短时，主要估计结果略小。

三是Phillips曲线滞后一年，滚动窗口提前10年时，模型表现最优。在此设定下，通胀的影响较明显，自然利率与产出缺口、潜在产出的趋势增长率的联动关系更为显著。

现实意义方面，在研究观察的156个月中，我国自然利率呈现出下降趋势。样本区间内的月度自然利率估计值的两个历史较低位分别位于2008年9月和2019年12月，与其相对应的估计值为1.06%和1.17%。

2008年全球金融危机过后，主要国家和地区将自然利率作为调控货币政策的重要参考，通过将市场基准利率维持在较低水平（Negro等，2017）[39]，收窄其与自然利率的差值，引导积极的货币政策发挥作用。

2008年9月，中国人民银行下调我国金融机构存款准备金率和贷款基准利率，持续释放流动性，至2019年11月，SHIBOR隔夜拆放利率降至自然利率下方，发挥了宽松货币政策的作用，避免了可能出现的经济剧烈下行，稳定了金融市场和经济社会发展。

2019年，全球经济增长再次放缓，经济发展的不确定性因素增加，中国人民银行及时调控货币政策，SHIBOR隔夜拆放利率与自然利率的差值逐步收窄，为社会提供流动性。随着货币政策效果逐步显现，为经济发展提供了有力支持。同时，将SHIBOR隔夜拆放利率保持在略高于自然利率的水平，为我国应对突发的外部冲击留有较充分的货币政策调控空间。

（二）研究展望

在全球长期低利率环境下，各国货币政策空间已被大幅压缩，近年各国通胀率高企，也增加了货币政策触及有效下限的可能，影响调控效果。我国持续推进利率市场化改革、加强定向支持、创新货币政策工具，不断提高货币政策调控的精确性能有效提高货币政策传导效率，促进市场发挥资源配置的作用。

随着我国利率市场化改革的不断深入，市场化的利率风险结构与期限结构不断完善，为自然利率纳入货币政策评价和调控提供了现实条件。自然利率既能够发挥货币政策调控“锚”的作用，又能反映潜在产出缺口和实际经济增长水平，可以为准确适度、合理灵活调控货币政策提供一定的量化依据。而月度自然利率提高了自然利率的估计频率，具备更加精准和及时的优势，有助于捕捉政策调控的最佳时机。

因此，将月度自然利率估计结果纳入货币政策评价体系并作为调控的量化依据之一，对我国货币政策调控实践具有重要参考意义，也有助于我国深化利率市场化改革。