基于Abaqus高支模墙柱支撑系统优化设计
2023-02-24张金山ZHANGJinshan
张金山/ZHANG Jin-shan
(中国水利水电第十一工程局有限公司,河南 郑州 450001)
在结构层高较大的混凝土工程施工中,高支模技术是使用较多的一种支撑系统。如地下轨道地铁站工程,因层高较大,高支模技术应用非常普及。高支模指搭设高度5m 及以上或搭设跨度10m 及以上或施工总荷载10kN/m2及以上或集中线荷载15kN/m 及以上或高度大于支撑水平投影宽度且相对独立无联系构件的混凝土模板支撑工程的总称。由于高支模是一种时变结构,它很容易造成整体或局部的失稳,严重时可能会造成整个高支模系统的失稳,从而造成大量的事故。在高支模设计的最初,可能会存在局部结构分布不够规范,部分支架分布间距可能合理但不够经济。关于高支模系统的设计,目前主要采用结构力学基本方法简化后,通过施工管理软件进行计算,构件初选多靠经验预设后校核计算,一般不进行方案对比等过程,可能会造成一定的浪费。
本文以深圳轨道交通某地铁站为研究对象,基于Abaqus 有限元分析软件,通过快速建模,在满足规范规定的结构强度、刚度和稳定性的条件下,以经济性评价为目的,对高支模墙柱支撑系统进行优化。
1 工程概况
深圳某地铁车站为地下二层式结构,站台宽11.0m,有效站台长度140m。标准段结构形式为地下二层单柱双跨钢筋混凝土框架结构,站后设交叉渡线。车站顶板覆土厚度约3.0~3.4m,车站主体结构为单柱双层双跨混凝土结构。车站侧墙厚0.7m,模板采用18mm 厚的胶合板,内楞100mm×100mm 木方竖向布置,间距200mm,外楞∅48.3×3.6 双钢管水向布置,上下间距初步设计为800m,整体对称布置。
高支模模板系统包括柱模板、板模板、梁模板、侧墙模板、剪刀撑以及顶托、扣件等,本文主要针对墙柱模板支撑系统开展研究。本工程共两层,支撑系统相互独立,文中选用较高一层的墙柱支撑系统进行设计优化。由于墙柱一面紧靠隧道,故模板支撑系统只做一面设计。
2 模型构建
2.1 数值模型构建
墙柱支撑系统采用钢管扣件式脚手架,整个墙面布置,主要由∅48.3×3.6 的扣件式钢管、面板、方木、剪刀撑等结构构成。在Abaqus 有限元软件分析中,交叉钢管之间连接的方式为旋转扣件,建模时设为铰接,钢管与地面的约束为铰接。单元类型采用曲面壳单元S4R(4 节点四边形有限薄膜应变线性缩减积分壳单元),钢材本构模型采用两折线弹塑性应力-应变曲线。支撑体系有限元模型见图1。
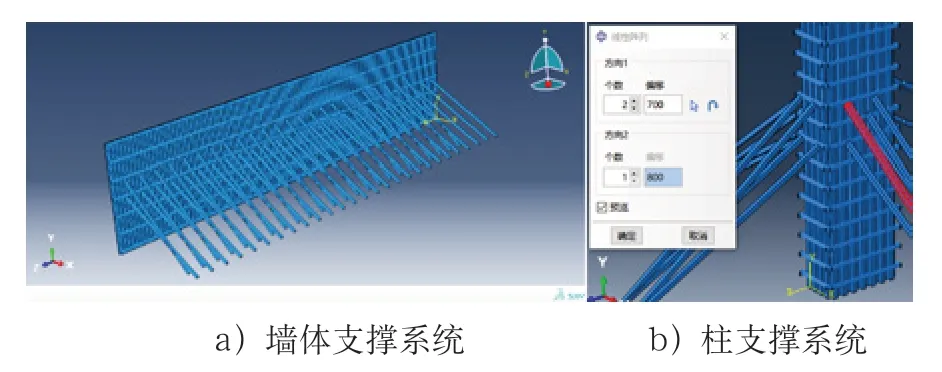
图1 墙柱支撑系统有限元模型图
2.2 支撑体系材料属性
支撑体系骨架均采用∅48.3×3.6 的扣件式钢管,材料为Q235 钢,材料属性如表1 所示。

表1 支撑系统材料属性表
2.3 支撑体系模型加载
支撑体系所受荷载直接作用在模型的侧面板上,荷载类型及组合方式根据JGJ 162-2008《建筑施工模板安全技术规范》、JGJ 130-2011《建筑施工扣件式钢管脚手架安全技术规范》及GB 50009-2012《建筑结构荷载规范》等相关规范规定的方式计算并按实际情况组合。加载后应力如图2 和图3 所示。

图2 墙模板局部应力云图

图3 墙模板局部应变云图
2.4 模型的合理性验证
为验证本文建立的有限元计算模型的准确性及适用性,对墙体支撑系统主梁(支撑方木的钢管,计算时截面取48.3mm×3.0mm)在组合荷载下弯矩进行计算。主梁截面抵抗矩W为4.49cm3,主梁弹性模量E为206000N/mm2,主梁截面惯性矩I为10.78cm4,主梁计算方式简化为为四等跨连续梁,主梁为两根。立杆间距及大梁间距均为700mm。
按传统结构力学简化方法计算,截面最大正应力σ=Mmax/W=83.96N/mm2。同样条件下,按Abaqus 有限元模型计算得出截面最大正应力σ=84.69N/mm2,误差小于2%,模型基本合理。
3 结构分析与优化
3.1 优化设计目标和变量
钢管的搭设间距直接与支撑体系强度、刚度及用钢量的大小相关。分析中以保证结构体系在满足规范允许的承载及变形能力条件下,用钢量最少为基本目标。调整的变量为支撑体系中的钢管的横向和纵向的间距,最终确定一个满足规范要求的合理骨架间距。
3.2 墙体支撑系统主梁跨度的优化
墙体支撑系统优化包括大梁跨度优化、大梁间距优化、斜撑布置优化等,这里仅以主梁跨度为例说明优化过程。通过有限元分析,分别计算可得出在不同的跨度下,结构的最大正应力σ,最大切应力τ,以及竖向挠度v,其中最大正应力变化情况见图4 所示。
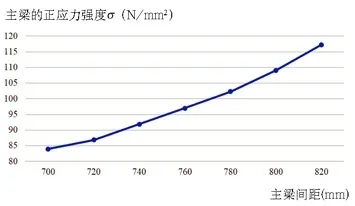
图4 主梁不同间距最大应力值比较
从图4 可以看出,最大正应力σ均小于抗弯强度设计值205N/mm2。同时计算侧向挠度均小于允许挠度。当主梁的跨度从700mm 增加到820mm 时,最大正应力和最大切应力值都呈增长趋势,且增幅先小后大;同样,竖向挠度随着主梁跨度的增大,挠度越来越接近允许挠度,并且增幅逐渐增大。由于墙体模板一段为悬挑构建,主梁间距一般不宜超过800mm。结合以上分析,悬挑式墙体支撑系统主梁跨度宜取800mm,基本满足规范及经济性要求。其他参数的优化过程方法类似。
3.3 独立柱支撑系统立杆间距的优化
柱支撑系统优化包含柱箍间距优化、立杆间距优化、对拉螺栓优化、斜撑布置优化等,这里仅以立杆间距跨度为例说明优化过程。由工程经验,立杆间距依次递增,分别取值700mm、750mm、800mm、850mm、900mm、950mm 进行分析。通过有限元分析,分别计算可得出在不同间距时,结构的最大正应力σ,最大切应力τ,以及竖向挠度υ,其中最大正应力变化情况如表2所示。
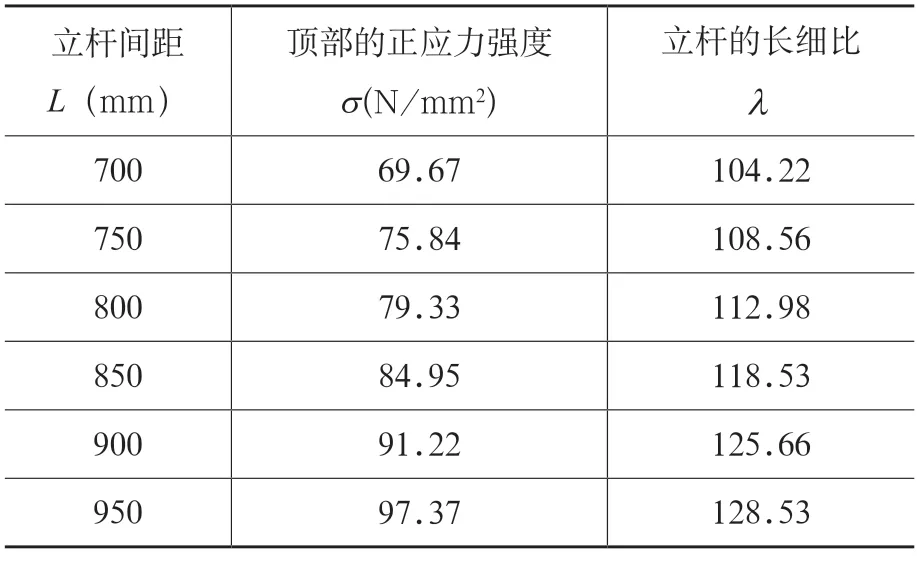
表2 立杆不同间距下参数
由表2 可以看出,立杆不同间距下的正应力强度均小于抗压强度设计值205N/mm2,且长细比均小于许用长细比[λ]=210。此外,当立杆的间距由700mm 逐渐增大到950mm 时,正应力强度和长细比也呈现递增趋势。根据JGJ 130-2011《建筑施工扣件式钢管脚手架安全技术规范》相关要求,结合柱的工程施工经验,立杆间距最大不宜超过900mm,基本满足规范及经济性要求。其他参数的优化过程方法类似。
4 结语
通过有限元软件Abaqus,建立了高支模墙柱支撑系统有限元模型,以某地铁站高支模为例,对不同支撑杆件参数进行了优化设计,得到如下结论。
1)通过有限元方法可简化计算过程,相比目前常用的结构力学简化计算方法,计算速度快,效率高。
2)经过优化设计,常规地铁站站台墙柱模板支撑体系中,在不考虑参数之间相互耦合的情况下,可能明确得出每种参数在满足规范要求的前提下最经济合理数据。可为类似工程施工设计提供一定参考。
