离散型随机变量数字特征的常见题型及处理策略

郭兴甫

(云南省曲靖市会泽县东陆高级中学)

离散型随机变量的数字特征是高中数学教材中的重要内容,也是每年高考命题的热点内容,题目难度中等偏上,题型多以解答题的形式出现,分值在12至17分之间.为帮助各位读者能在高考复习中更好地掌握这部分内容,本文以近年的高考及模拟题为例说明这部分内容的常见题型及处理策略,供复习参考.

1 离散型随机变量分布列的性质及其应用

例1(1)若离散型随机变量X的分布列为

(2)(多选题)已知m,n均为正数,随机变量X的分布列如表1所示,则下列结论一定成立的是( ).

表1

A.P(X＝1)＜P(X≠1)

B.E(X)＝1

D.D(X＋1)＜1

综上,选BCD.

2 求离散型随机变量的分布列

例2已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.

(1)求第一次检测出的是次品且第二次检测出的是正品的概率;

(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列.

(2)X的可能取值为200,300,400,则

故X的分布列如表2所示.

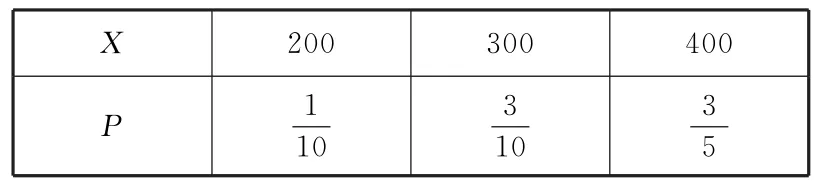
表2

3 求离散型随机变量的均值与方差

例32022年世界乒乓球团体锦标赛于9 月30日至10月9日在成都举行.近年来,乒乓球运动已成为国内民众喜爱的运动之一.今有甲、乙两位选手争夺乒乓球比赛冠军,比赛采用三局两胜制,即某位选手率先获得两局胜利时比赛结束.根据以往经验,甲、乙在一局比赛获胜的概率分别为,且每局比赛结果相互独立.

(1)求甲获得乒乓球比赛冠军的概率;

(2)比赛开始前,工作人员买来两盒新球,分别为“装有2个白球与1个黄球”的白盒与“装有1个白球与2个黄球”的黄盒.每局比赛前裁判员从盒中随机取出1个球用于比赛,且局中不换球,该局比赛后,直接丢弃.裁判按照如下规则取球:每局取球的盒子颜色与上一局比赛用球的颜色一致,且第一局从白盒中取球.记甲、乙决出冠军后,两盒内白球剩余的总数为X,求随机变量X的分布列与数学期望.

记事件A:“甲夺得冠军”,则

记Wi表示第i局从白盒中抽取的白色球,Yi表示第i局从黄盒中抽取的黄色球,X的所有可能取值为1,2,3,所以

综上,X的分布列如表3所示.

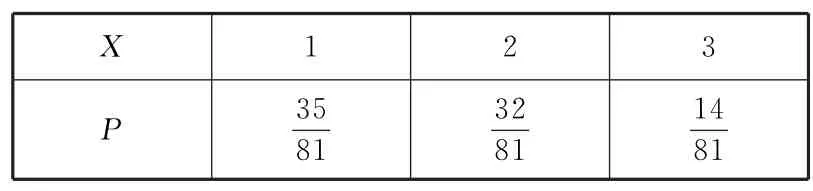
表3

例4教育部门出台了“双减”政策,即有效减轻义务教育阶段学生过重作业负担和校外培训负担,持续规范校外培训(包括线上培训和线下培训).“双减”政策的出台对校外的培训机构经济效益产生了严重影响.某大型校外培训机构为了规避风险,寻求发展制订科学方案,工作人员对2022年前200名报名学员的消费金额进行了统计整理,其中数据如表4所示.

表4

(1)该大型校外培训机构转型方案之一是将文化科辅导培训向音体美等兴趣爱好培训转移.为了深入了解当前学生的兴趣爱好,工作人员利用分层抽样的方法在消费金额为[9,11)和[11,13)的学员中抽取了5人,再从这5人中选取3人进行有奖问卷调查,求抽取的3人中消费金额为[11,13)的人数的分布列和数学期望.

(2)以频率估计概率,假设该大型校外培训机构2022年所有学员的消费金额可视为服从正态分布N(μ,σ2),μ,σ2分别为前200名报名学员消费金额的平均数ˉx以及方差s2(同一区间的花费用区间的中点值替代).

(ⅰ)试估计该机构学员2022 年消费金额为[5.2,13.6)的概率(保留一位小数);

(ⅱ)若从该机构2022年所有学员中随机抽取4人,记消费金额为[5.2,13.6)的人数为η,求η的方差.

X的分布列如表5所示.

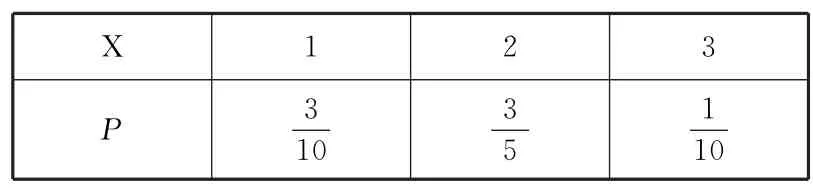
表5

(2)(ⅰ)由题意得

4 随机变量均值与方差在决策中的应用

例5某公司圆满完成预定的生产任务,为答谢员工的辛勤努力,公司决定在联欢晚会后,拟通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有4种面值的奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.

(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;

(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一种方案是2张面值20元和2张面值100元;第二种方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好? 并说明理由.

所以P(X＝80)＝P(X＝120),故员工获得80元奖励额与获得120元奖励额的概率相等.

(2)第一种方案为(20,20,100,100),设员工所获得的奖励额为X1,则X1的可能取值为40,120,200,所以

所以X1分布列如表6所示.

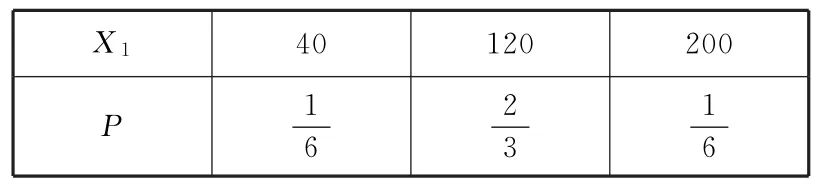
表6

第二种方案为(40,40,80,80),设员工所获得的奖励额为X2,则X2的分布列如表7所示.

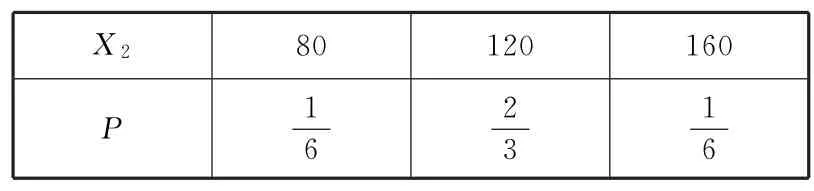
表7

又因为500E(X1)＝500E(X2)＝60000元,所以两种方案奖励额的数学期望都符合要求,但第二种方案的方差比第一种方案的小,故应选择第二种方案.

例6在中国共产党的正确领导下,我国顺利实现了第一个百年奋斗目标——全面建成小康社会.某地为了巩固扶贫成果,决定继续对甲、乙两家乡镇企业进行指导.指导方式有两种,一种是精准指导,一种是综合指导.已知对甲企业采用精准指导时,投资50万元,增加100万元收入的概率为0.2,增加200万元收入的概率为0.8,采用综合指导时,投资100万元,增加200万元收入的概率为0.6,增加400万收入的概率为0.4;对乙企业采用精准指导时,投资50万元,增加100万元收入的概率为0.3,增加200万元收入的概率为0.7,采用综合指导时,投资100万元,增加200万元收入的概率为0.7,增加400万元收入的概率为0.3.指导结果在两家企业之间互不影响.

(1)若决策部门对甲企业进行精准指导、对乙企业进行综合指导,设两家企业增加的总收入为X万元,求X的分布列;

(2)若有150万元无息贷款可供甲、乙两家企业使用,对两家企业应分别进行哪种指导总收入最高?请说明理由.

故当决策部门对甲企业进行精准指导、对乙企业进行综合指导时,两家企业增加的总收入X的分布列如表8所示.

表8

(2)指导方案1:对甲、乙两家企业均进行精准指导.设两家企业增加的总收入为Y万元,则Y的可能取值为200,300,400,且

指导方案2:对甲企业进行精准指导、对乙企业进行综合指导.

由(1)可得E(X)＝300×0.14＋400×0.56＋500×0.06＋600×0.24＝440.

指导方案3:对甲企业进行综合指导、对乙企业进行精准指导.

设两家企业增加的总收入为Z,则Z的可能取值为300,400,500,600,且

因为350＜440＜450,故选择指导方案3,即对甲企业进行综合指导、对乙企业进行精准指导总收入最高.

5 分布列、均值与方差的创新应用

例7某汽车公司最近研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如图1所示的频率分布直方图.

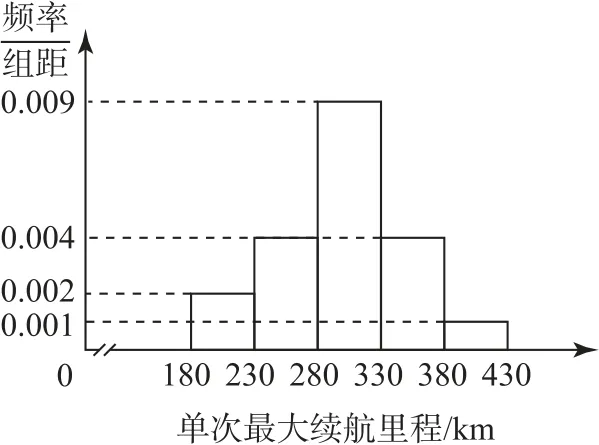
图1

(1)估计这100辆汽车的单次最大续航里程的平均值xˉ(同一组中的数据用该组区间的中点值代表);

(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航量程X近似地服从正态分布N(μ,σ2),经计算第(1)问中样本标准差s的近似值为50.用样本平均数作为μ的近似值,用样本标准差s作为σ的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250km 到400km 之间的概率;

(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正、反面的概率都是,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从k到k＋1),若掷出反面,遥控车向前移动两格(从k到k＋2),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第n格的概率为Pn,试证明{Pn－Pn－1}(1≤n≤49,n∈N∗)是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.

参考数据:若随机变量ξ服从正态分布N(μ,σ2),则

(2)由(1)及条件可得X～N(300,502),所以

(3)遥控车开始在第0格为必然事件,P0＝1,第一次掷硬币出现正面,遥控车移到第一格,其概率为

遥控车移到第n(2≤n≤49)格有两种可能:①遥控车先到第n－2格,又掷出反面,其概率为②遥控车先到第n－1 格,又掷出正面,其概率为,所以

链接练习

1.已知随机变量X～B(6,p),Y～N(μ,σ2),且P(Y≥2)＝,E(X)＝E(Y),则p＝( ).

2.某围棋学校选拔参加围棋大赛选手的规则如下:①每位参加者都要依次和A,B,C,D四位大师进行四场比赛;②每场比赛参赛选手只有获胜和失败两种结果,若获胜,则该场比赛依次得1分,1分,1分,3分;若失败,则该场得0分;③四场比赛结束后,累计得分大于或等于5分,则成为围棋大赛选手;小于5分时,则不能成为围棋大赛选手.学生甲和A,B,C,D四位大师进行比赛,获胜的概率依次为,且各场比赛相互之间没有影响.

(1)求学生甲成为围棋大赛选手的概率;

(2)设学生甲最后累计得分为X,求X的分布列和数学期望.

链接练习参考答案

1.B.

(2)随机变量X的分布列如表9所示.

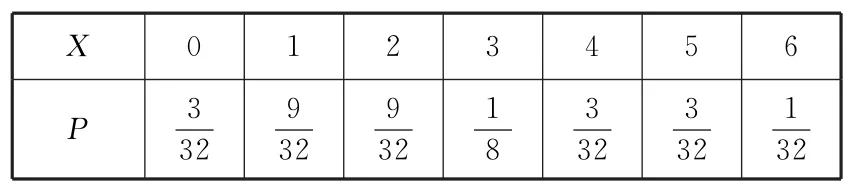
表9

(完)