恰当选择研究角度,巧妙破解排列组合问题

俞 纲 周继波

(1.云南省昆明市第三中学 2.云南省昆明市第十六中学)

排列组合与计数问题的计算是围绕着事件的完成来展开的,而完成事件的角度往往不止一种.从不同的角度来完成事件其复杂程度各不相同,这就需要我们多思考、多总结,学会选择恰当的角度来完成事件,以达到事半功倍、化繁为简的效果.

例1学校安排全校六个年级的同学去春游,有四个公园可供选择,每个年级去一个公园,则共有多少种不同的安排方法?

例2从甲、乙、丙、丁、戊、己六人中选四人去四所学校学习,每人去不同学校,其中甲不能去A学校,则有多少种不同的安排方法?

例3经过正方体任意两个顶点的所有直线中,异面直线共有多少对?

例4(1)四个人坐一排八个座位,其中恰好有两个空座位相邻,则有多少种不同方法?

(2)八人参加100米比赛,没有并列,其中甲、乙比丙、丁、戊先到达有多少种不同情况?

(2)如果直接用位置分析法或元素分析法,都要通过列举法把满足条件的形式列出来,这样相对麻烦;如果把问题形象看成按照甲、乙在前,丙、丁、戊在后的结构确定五人相对位置,再依次插入另外三人,则后三人的插入不会改变前五人的相对顺序,问题得到巧妙解决,但值得注意的是,后三人可以相邻,因此插入时要“先后逐一”插入,即每插入一人,空隙就会增加一个,则情况数为.此题还可以研究甲、乙、丙、丁、戊五人的任意排序中满足甲、乙在丙、丁、戊前面的概率,则八人任意排序中,满足条件的情况数为4032种.

例5甲、乙、丙、丁等七人各自选择周一至周日中的一天值日,每人选择不同的一天.

(1)甲不在周一,乙不在周日,则共有多少种安排方法?

(2)甲不在周一,乙不在周日,且若丙在周三,则丁不在周四,则有多少种不同的安排方法?

由此用间接法计算可得情况数为

(2)由于条件语句的逻辑关系比较复杂,在七人全排列的角度下,无论是正面研究还是用间接法都比较烦琐.这时我们可以把研究角度聚焦在第(1)问的范围内,用集合语言来描述,即

即用“甲不在周一且乙不在周日”的总情况数减去“甲不在周一乙不在周日且丙在周三丁在周四”的情况数,则可以直接计算出情况数为

例6某小组十个人中只会唱歌的有三个人,只会跳舞的有三个人,既会唱歌又会跳舞的有四个人,从中选出不同的三个人去唱歌,三个人去跳舞,有多少种不同的选法?

例7如图1所示,在六个区域中涂上颜色,有五种颜色可供选择,要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法总数为多少种?

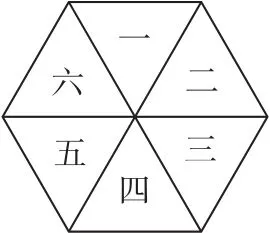
图1

例8甲、乙、丙、丁、戊、己六位同学的六张试卷放在一起,每人拿一张试卷,恰好所有同学都拿错试卷的情况共有多少种?

而通过列举法,我们得到k(2)＝1,k(3)＝2,从而k(4)＝9,k(5)＝44,k(6)＝265,问题得到解答.

(完)