基于FPGA 的北斗时统设备铷钟驯服技术实现

何文彦HE Wen-yan；雷正伟LEI Zheng-wei；甄红涛ZHEN Hong-tao；李凯丽LI Kai-li；刘雅迪LIU Ya-di

（①西安航光卫星测控技术有限公司，西安 710100；②西安电子科技大学，西安 710100）

0 引言

在我国军事和航天领域中，导航定位和授时系统在北斗信息服务中占据着越来越重要的地位。而时钟同步是精密授时的根本保证[1]。铷钟短期稳定度较好，是常用的同步原子时钟[2-4]。时间统一系统包含时统中心和若干时统分中心，是为测控系统提供统一标准时间信号和标准频率信号的系统，其设备由无线电接收机、原子频率标准、标准信号发生器和放大分配设备组成，无线电接收机通过接收卫星信号校准本地铷钟频率[5]。世界各国以性能优异的原子钟建立并保持着本国的时间体系。高精度时间统一系统设备作为授时设备，能够通过不同的链路接口对不同的设备进行授时。本文分析了一种北斗时统设备铷钟驯服技术，该技术基于FPGA 获取铷钟钟频差值，并利用vondrak 滤波和kalman 滤波算法对钟差值进行处理，然后利用PID 控制算法对铷钟电压进行控制，调节铷钟频率，实现时间同步、提高守时设备精度。

1 铷钟驯服技术实现原理

铷钟驯服技术由FPGA 和MCU 实现。FPGA 根据时间间隔测量原理，计算北斗接收机的秒脉冲与铷钟分频的秒脉冲差值，并采用kalman 算法和vondrak 算法联合对此钟差值滤波，再通过uart 发给MCU；MCU 通过PID 控制算法，对DAC 转换芯片进行精准的电压控制，从而准确地改变铷钟频率，达到驯服铷钟的目的。

1.1 时间间隔测量原理 时间间隔测量由FPGA 实现，原理如图1 所示，TX为测量时间间隔值，T0为采用时钟计数法计算出的时间间隔值，计数法存在量化误差：T1（开始信号与计数时钟信号不同步部分）和T2（结束信号与计数时钟信号不同步部分），关系如下：

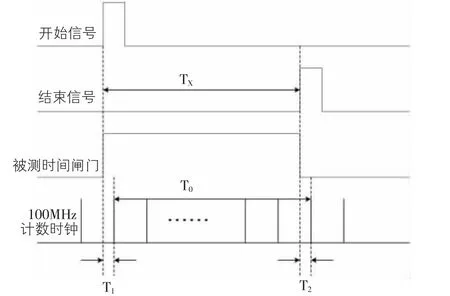
图1 时间间隔测量原理图

T1和T2两值可由时间-幅度转换法计算。计数法参考时钟为铷钟倍频的100MHz 时钟，若其在由开始信号和结束信号构成的时间闸门内计得时钟个数为N0，则T0=N0×T，这里T 为10ns。若时间闸门内时钟个数理论值为N，则钟差值为：±（N-N0）/TX。

1.2 kalman 滤波原理 kalman 滤波算法以最小均方误差为准则，根据前一估计值和最近一观察数据进行估计信号当前值。所以该算法无需知道过去全部观察数据，采用状态方程和迭代方法，以估计值的形式给出滤波值。

图2 递归描绘最小均方估计问题

kalman 滤波算法有时间更新和测量更新两部分，时间更新有两个预测方程：

测试更新有三个状态方程：

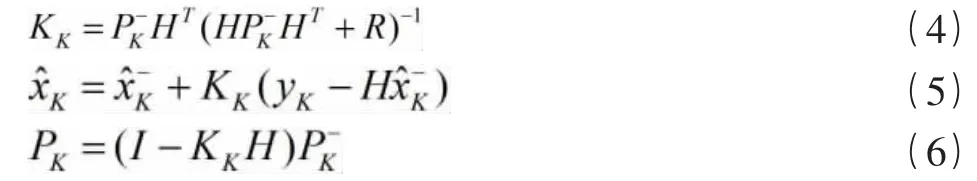
本项目中，需要根据钟差实测值和滤波效果，调节过程噪声协方差Q 和测量噪声协方差R。时间更新的两个公式通过在上一次的钟差数据计算最优化估计和其协方差的基础上，进行预测计算，得出此次的钟差数据最优估计和其协方差的预测值。在式（2）中，为钟差数据的预测值，A 为状态矩阵，为上一次钟差数据得到的最优估计，B 为控制矩阵，uK-1为控制输入。在式（3）中为钟差数据的预测值的先验估计协方差，A 为状态转移矩阵，为了简便计算，A 和AT取1。Q 为过程噪声的方差，是需要根据实验和仿真滤波效果，对此参数进行确定。

状态更新的三个公式，分别计算了本次钟差数据的卡尔曼增益、最优估计以及最优估计的协方差矩阵。在式（4）中，因为，卡尔曼增益KK可以扩展为：

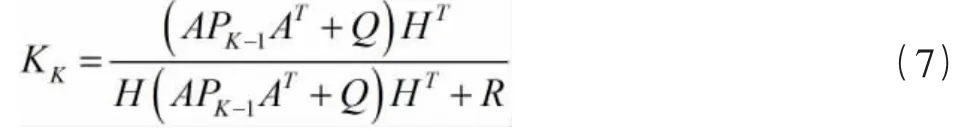
为了简便运算，取维数矩阵H 和状态矩阵A 为1，因此HT和AT也为1，可得简化的卡尔曼增益为：

可根据式（8）对Q 和R 参数进行调节，从而可以调整卡尔曼增益KK的大小。在式（5）中为此次钟差数据的最优估计，调整卡尔曼增益KK可以调整预测值和观测值yK的占比，从而调整出最优估计值。在式（6）中，最优估计协方差矩阵PK可以通过卡尔曼增益KK和最优估计协方差矩阵估计值得到[6]。

此滤波算法在FPGA 中实现，INT_FLOAT 模块将输入钟差数据转换为符合IEEE 754 标准的浮点数，Kalman_forecastOne 模块和Kalman_forecastTwo 模块分别完成了对钟差数据的预测值以及钟差数据的预测值的先验估计协方差和卡尔曼增益的计算，Kalman_update 模块完成钟差数据的最优估计以及其协方差矩阵的计算，最后通过模块FLOAT_TO_INT 模块将计算得出的最优估计转换为整数输出。

1.3 vondrak 滤波原理 vondrak 滤波在不知道观测数据变化规律及其拟合函数时，就能对观测数据平滑滤波。基本思想：通过不同的平滑因子控制数据的平滑程度，在绝对拟合与绝对平滑间选择一条折衷的曲线，保留有用信号，滤除噪声信号。

修匀数学中指出一个修匀序列满足光滑性要求，所谓光滑性要求，就是在满足S 很小的情况下，所得出的修匀值位于一条光滑的曲线上[7]。

实际处理时，过度追求光滑性会使估计值偏离原始观测值，则处理的结果与真值的偏离程度增大。可预先采用一定的处理方法，去除粗大误差，使得观测值与真值的偏离程度很小。

考虑到整体加权及正负抵消的情况下，令

上式中F 为拟合度，yi为观测值，为修匀值。当F 为0 时，说明与yi完全重合，则没有起到修匀效果。

Whittaker 于1923 年将式（9）、式（10）做了线性组合，发展为Whittaker 修匀：

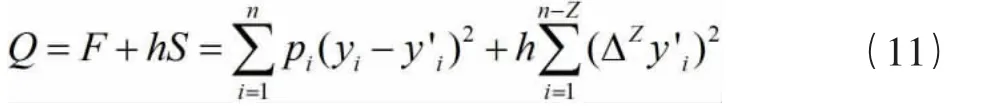
其中：pi为观测值的权序列，yi为观测值序列，为平滑值序列，h 是正常数。上述准则下得到的修匀值既满足位于一条光滑的曲线上，又与原观测序列具有一定的拟合度。

捷克天文学家J.Vondrak 对Whittaker 修匀进行改进为Vondrak 滤波：

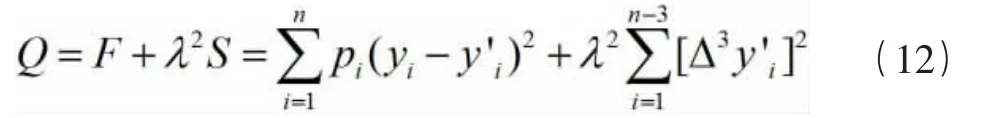
1976 年再对上式进行了改进，将拟合度和平滑度分别用平均值来代替，得：

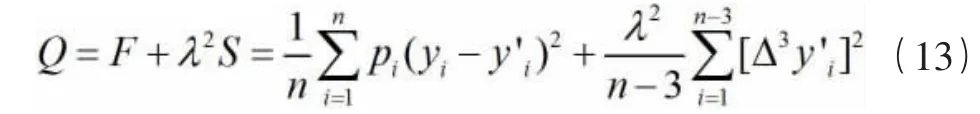
其中，pi为观测值的权序列，yi为观测值序列，为平滑序列，λ 是正常数为平滑因子（一个给定的无量纲的正数），在观测数据的绝对拟合和绝对平滑之间起着平衡的作用，ε 越小，曲线的平滑程度越强[8]。

1.4 PID 控制原理 PID 控制是一种线性控制器，将系统的输出偏差进行线性组合构成控制量，对系统进行反馈调节，原理框图如图3 所示。常用的PID 算法模型包括增量式算法、位置式算法、微分先行法三种。本次铷钟驯服采用增量式算法对铷钟控制电压进行调节。

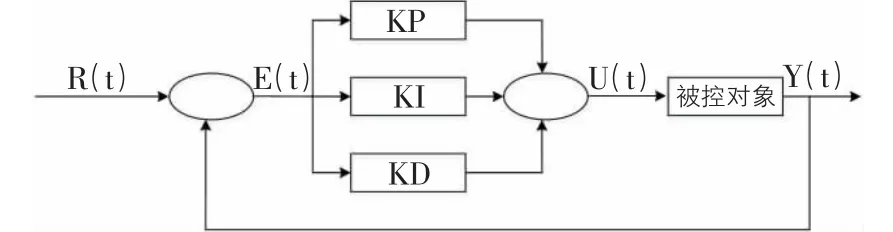
图3 PID 控制原理框图

PID 算法模型：

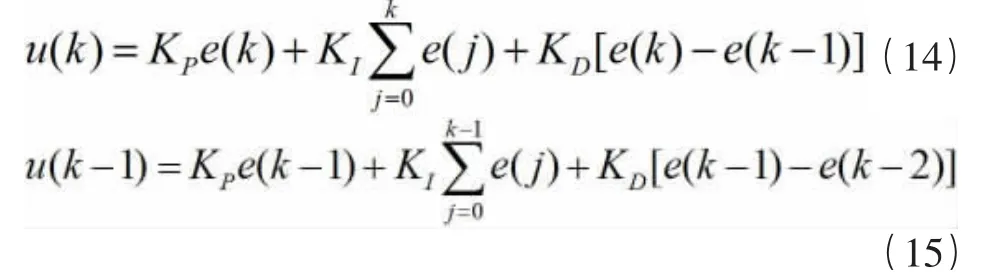
u（k）为控制器的输出值，e（k）为控制器输入值与设定值之间的误差。KP为比例系数，KI为积分时间常数，KD为微分时间常数。用式（14）减去式（15），可得：

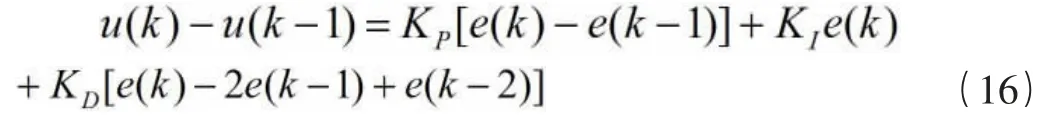
式（16）称为增量式PID 算法，Δu（k）为控制器输出控制量的变化。

对于铷钟电路上DAC 模块控制电压的输入数据，首先，设定KP、KI、KD的初值以及压控电压初始值。对于驯服铷钟来说，e（k）为当前测量得到的相差，即需获取的测量输入值。再计算增量误差：

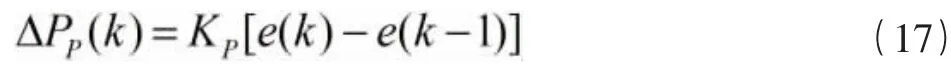
积分误差：

微分误差：

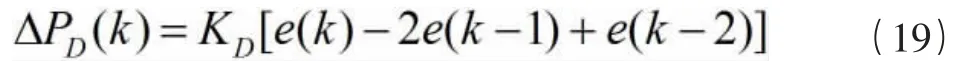
得到本次PID 的输出值：

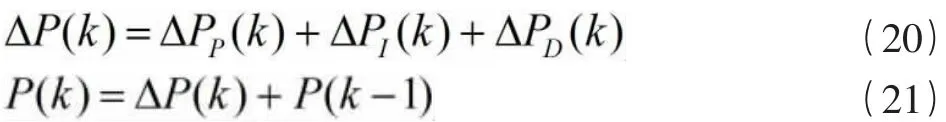
得出更新误差值：

PID 参数互相影响，调试过程中可根据情况对积分系数、比例系数、微分系统进行细调。经实际试验与测试，设备PID 参数设置：比例系数P=0.1，积分系数I=0.15，微分系数D=0.1，即P=0.1，I=0.15，D=0.1。

1.5 铷钟内部原理 铷原子钟内部原理如图4 所示，由量子部分和压控晶体振荡器组成。压控晶振的频率经过倍频和频率合成器送到量子系统与铷原子跃迁频率进行比较，并将误差信号送回压控晶振，使其锁定在铷原子特定的能级跃迁至对应的频率上[9]。

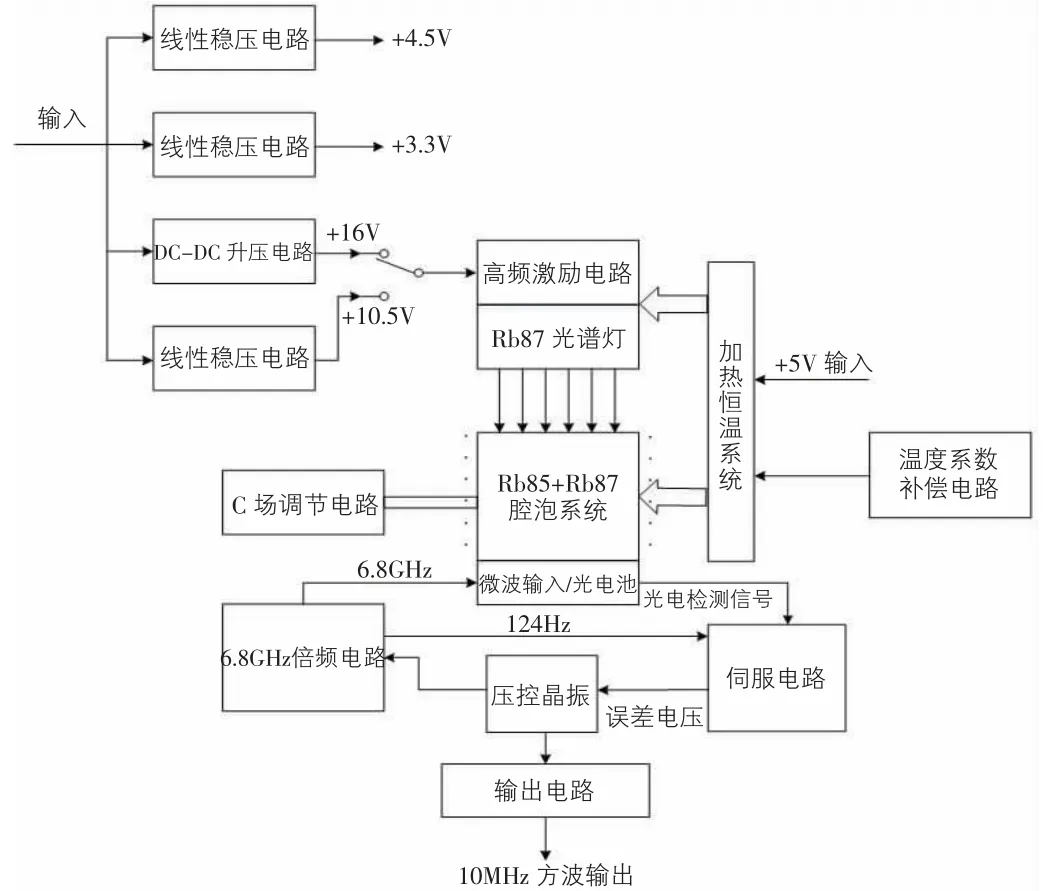
图4 铷钟内部原理图

2 铷钟驯服模块硬件组成

北斗接收机对接收的卫星信号进行解码、滤波，输出标准1PPS 信号至FPGA。FPGA 测量出标准1PPS 与铷原子钟分频产生的1PPS 之间的差值，并将滤波处理的真实差值发送给MCU，MCU 通过控制算法得到铷原子钟控制电压的控制量，并发送给高精度D/A 转换器，转换得电压值发送至铷原子钟，继而调节铷钟输出频率，使其产生的1PPS 信号与北斗卫星信号的1PPS 信号误差不超过一个时间周期，实现对铷钟频率的驯服。

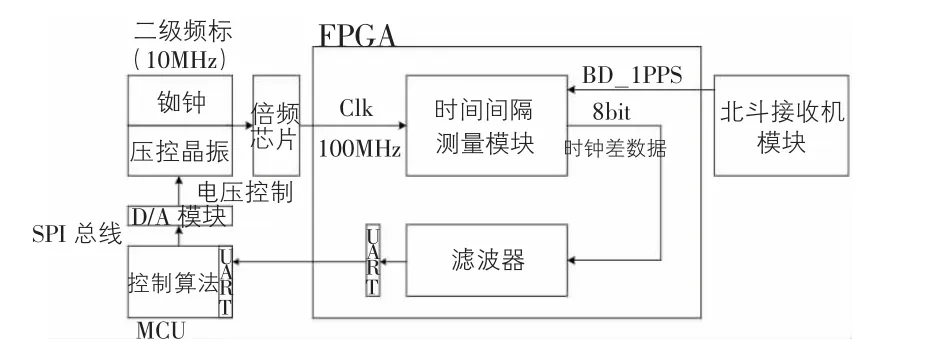
图5 铷钟驯服原理图

3 测试数据分析

本守时设备以北斗1PPS 信号作为频标信号进行比较和分析，对铷原子钟分频产生的1PPS 信号进行准确度分析和对比。图6 为kalman+vondrak 滤波后钟差数据、单独kalman 滤波后钟差数据与原始钟差数据对比。对比结果表明，kalman+vondrak 滤波对原始钟差数据进行了较好的平滑和预测，使其在卫星信号失效情况下仍能较为准确地对铷钟进行电压控制。室温环境下，测试本时统设备一天的守时精度。设备测试起始测量值208ns，设备测试24 小时之后的测量值为4.40us。根据测量出的数据可得，室温环境下设备的守时精度为4.2us。

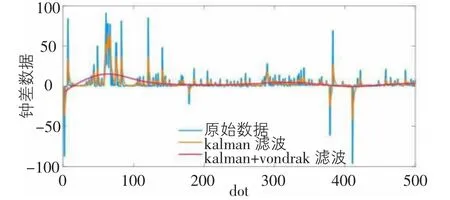
图6 kalman+vondrak 滤波后钟差数据、kalman滤波后钟差数据、原始数据数据对比

4 结论

通过研究铷原子钟驯服原理，提出了基于FPGA 的北斗时统设备铷钟驯服实现方法。以北斗接收机输出时间频率为参照，测量铷钟钟差值，对钟差值滤波前后数据进行多次比对测试。测试数据表明，结合kalman 滤波和Vondrak 滤波算法对钟差值数据的滤波效果，比单独采用kalman 滤波算法更好，为铷原子钟驯服提供了技术依据，可以较好地实现时间同步和提高守时设备精度。