基于多层连通性模型的动态调控参数优化方法
2023-02-22单高军
单高军
中国石油大庆油田有限责任公司勘探开发研究院,黑龙江 大庆 163000
为实现油田高效开发,需要制定符合现场实际情况且可操作性强的开发方案。在制定方案的过程中,同时也需要考虑如储层性质[1-3]、流体性质[4]、市场供求[5]、政策要求[6]、经济因素[7]等方面的制约因素。因此,为改善油藏生产控制,进一步完善油藏管理水平,相关学者深入研究了“油藏闭合生产优化管理技术”这一理念[8-11]。目前,我国多数老油田存在多井、多层系、多次井网加密等复杂开发情况[12-14],平面及层间矛盾突出,“油藏闭合生产优化管理技术”急需考虑这种油水渗流的复杂关系。鉴于此,笔者提出基于多层连通性模型动态调控参数优化方法,以井间连通单元为对象建立物质守恒方程,通过压力求解获得井间流量分布,饱和度追踪实现井点处油水动态计算,与单层连通性模型相比,能够验证、指导和修正储层平面及纵向的非均质性及地质连通状况,为数值模拟历史拟合、剩余油分布挖潜、稳油控水策略制定提供准确的油藏储层信息及数据支持。
1 多层连通性模型

图1 基于多层连通性模型的动态调控参数优化方法流程图Fig.1 Flowchart of optimization method for dynamically controlling parameters based on multi-layer connectivity model
基于多层连通性模型动态调控参数优化方法的主要流程如图1所示,主要包括两部分:模型参数拟合和开发方案优化。首先,以油田生产系统为主要对象,采用连通性数值模拟技术,自动拟合生产数据,进而动态修正连通性模型参数,降低模型不确定性;其次,基于不断修正后的连通性模型以及连通性数值模拟技术,采用优化控制算法动态优化模拟开发过程,预测油田生产最优工作制度,实现效益最大化。
2 参数拟合
2.1 压力及井间流量计算
针对多井多层系复杂渗流体系,考虑连通单元内注水井注水量、采油井采液量、流体重力以及油、水、岩石压缩性,并忽略层间窜流、毛细管力作用,以多层生产或注入的第i口井为研究对象,列出油藏条件下物质守恒方程为:
(1)
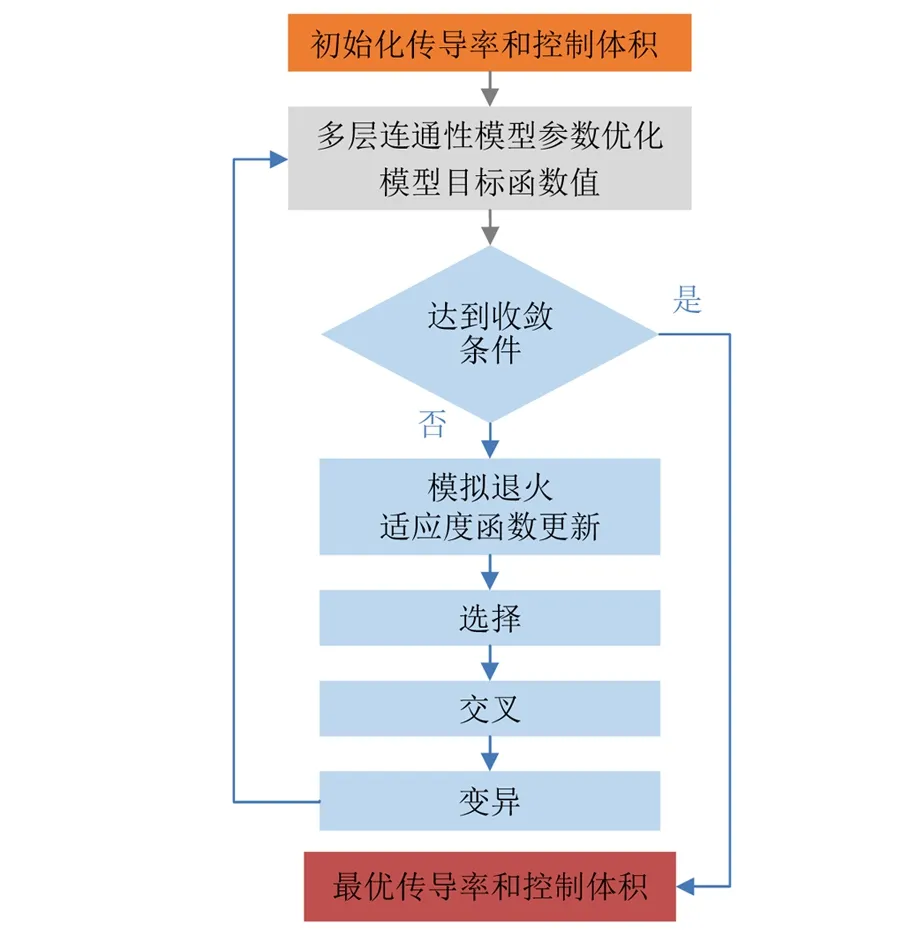
式中:Tijk(t)为第i井和第j井第k层井间综合传导率,m3/(d·MPa);pi(t)为i井在泄油区内的压力均值,MPa;pj(t)为j井在泄油区内的压力均值,MPa;α为单位转换系数,1/1000000;ρl为液体密度,kg/m3;g为重力加速度,m/s2;Dijk为i井和j井第k层高差,m;qi(t)为i井注采量,注入为正、产出为负,m3/d;Ctk为第k层综合压缩系数,1/MPa;Vpik(t)为i井第k层连通体积,m3;Nk为总层数;N2为总注采井数;t为生产时间,d。
整理式(1)可得:
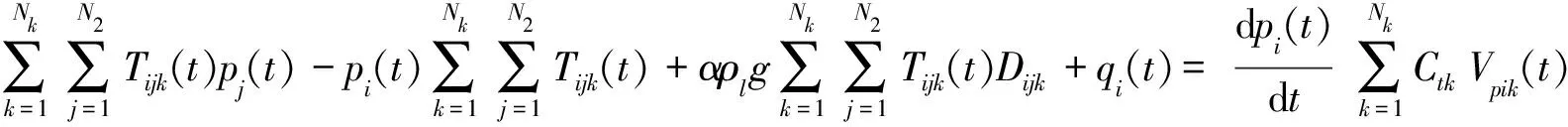
(2)
对式(2)进行隐式差分可得:
(3)
根据渗流理论,传导率和连通体积随时间而改变,可根据上一时刻压力或饱和度进行估算:
(4)
(5)
式中:Aijk为第i井和第j井在第k层渗流截面积均值,m2。
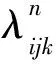
(6)
式中:Kijk为第i和j井在第k层的渗透率均值,mD;Kro为油相相对渗透率,1;Krw为水相相对渗透率,1;μok为第k层的油相黏度,mPa·s;μwk为第k层的水相黏度,mPa·s。
2.2 含水饱和度追踪计算
本文模型中,假设连通单元内渗流行为符合稳定渗流特征,即一维油水两相渗流。根据 Buckley Leverett 前沿推进理论[15],注水端任意位置的含水饱和度与累计流量满足:
(7)
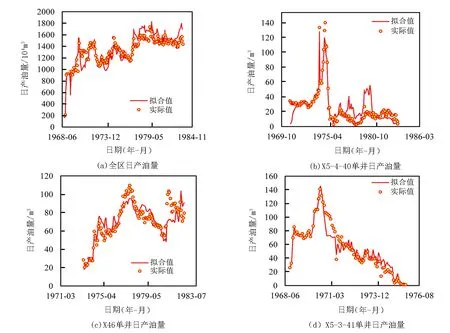
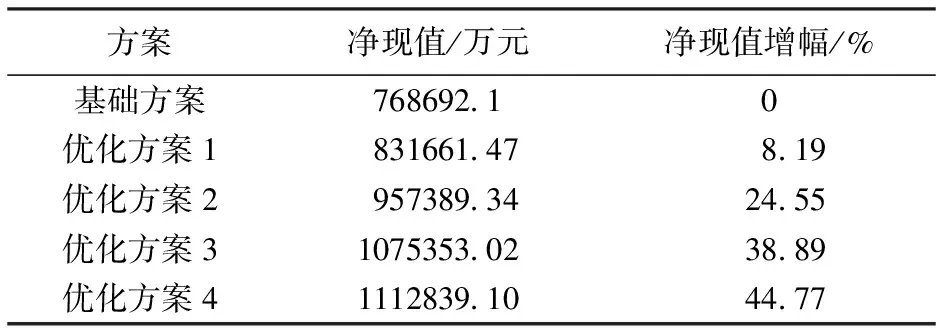
另取一点xu,其为x的上游点,满足xu (8) 由式(7)、式(8)可得, (9) 定义Fv为从xu流入到x的无因次累计流量,即: (10) 则由式(10)可得: (11) 在建立的连通性模型的基础上,优化求解模型参数,使模型计算动态与实际生产一致,进而能够进行动态预测及水驱效果评价。定义如下最小化问题: (12) 满足: m≥0 (13) (14) 式中:m为模型参数组成的向量;mpr为先验模型估计;CM为模型参数协方差矩阵;dobs为实际井产液数据;g(m)为模型预测动态数据;CD为误差协方差矩阵;VR为油藏总孔隙体积,m3。 图2 基于遗传退火进化算法的连通性参数优化Fig.2 Connectivity parameter optimization based on genetic annealing evolutionary algorithm 针对式(12)~(14)的最小化问题,采用遗传退火进化算法进行求解。其主要原因是遗传算法虽具有良好的全局搜索能力,但在实际应用中,容易产生早熟收敛的问题,而模拟退火算法能够改善遗传算法的这一缺陷。两种算法结合求解具有全局最优性和计算高效性等优势。本文基于遗传退火进化算法的连通性参数优化步骤如图2所示: ①初始化传导率和控制体积;②初始化遗传算法;③计算所有种群的适应度;④如果达到最大代数或者已经收敛,转到步骤⑤,否则对适应度进行模拟退火操作,进行选择、交叉和变异遗传操作算子,转到步骤③;⑤已经收敛,得到最优传导率和控制体积。 其中遗传算法所有种群适应度计算完成后,步骤④中对适应度进行模拟退火操作: T=T0αk (15) (16) 式中:T为每代个体的退火温度;T0为初温;k为当前代;Fit(i)为第i个种群的适应度;Fmax为当前代所有种群的最大适应度。 基于历史拟合后的连通性模型为动态预测基础,将未来油水井工作制度作为控制参数,结合约束条件,建立净现值单目标生产优化控制模型,能够同时考虑产油收益、注水以及产水处理的费用。 净现值单目标最大函数为: (17) 图3 基于遗传退火进化算法的生产优化Fig.3 Production optimization based on genetic annealing evolutionary algorithm 满足: ei(u)=0 cj(u)≤0 基于遗传退火进化算法对单目标函数进行注采生产优化,优化步骤如图3所示:①初始化注采参数;②初始化遗传算法;③计算所有种群的适应度;④如果达到最大代数或者已经收敛,转到步骤⑤,否则对适应度进行模拟退火操作,进行选择、交叉和变异遗传操作算子,转到步骤③;⑤已经收敛,得到最优注采参数。 图4 井间连接图Fig.4 Interwell connection diagram 目标区块具有含油井段长、发育层数多、单层厚度薄等特点,平均单井钻遇砂岩厚度55.77m,有效厚度15.33m,共有油井36口,转注井15口,水井3口。统计各井静动态资料后,在自编软件中生成井间连接图,油水井采用直线相连,表征油-水井以及油井之间的连接情况,如图4所示。同时,为确保水井注入水不会波及距离过远的油井,造成偏离物理意义的计算结果,油-水井以及油井之间的直线相邻连接夹角要小于15°。 基于连通性数值模拟技术,对现有生产数据进行自动历史拟合,如图5所示,全区以及单井日产油的历史拟合精度较高,进一步说明井间连通性模型参数设置较为可靠。 图5 目标区产油量拟合曲线Fig.5 Fitting curves of oil production in the target area 基于目标区块历史拟合后的连通性模型,设计优化不同开发井、不同注采生产制度的对比开发方案。各方案均预测开采五年后,模拟累计产油和净现值增幅情况。 基础方案:在连通性拟合结束时产液和注水量的情况。 优化方案1:产液量最小为0,最大为连通性拟合结束时产液量的1.5倍,只优化油井。 优化方案2:注水量最小为0,最大为连通性拟合结束时注水量的1.5倍,只优化水井。 优化方案3:注采量最小为0,最大为连通性拟合结束时产液和注水量的1.3倍,油水井同时优化。 优化方案4:注采量最小为0,最大为连通性拟合结束时产液和注水量的1.5倍,油水井同时优化。 基于连通性的生产优化模型,对基础方案和优化方案进行了模拟,得出了预测年限的累计产油和净现值,计算结果如表1、表2所示。可以看出,优化后生产指标较好,累计产油和净现值不断增加,其中优化方案4效果最好,全局最优解。 表1 累计产油统计 表2 净现值统计 1)针对我国陆上老油田井多、层系多、多次井网加密等复杂渗流情况,基于油水井物质守恒方程和Buckley-Leverett前缘推进理论建立了多层连通性模型。 2)通过自动历史拟合求取多层连通性模型参数,对油水井动态进行快速预测。基于多层连通性模型建立调控优化模型,实现了研究区块的快速生产优化。 3)将基于多层连通性模型的动态调控参数优化方法应用到目标区块调整方案设计中,与基础方案相比,五年增产原油433.82×104m3,增幅42.84%,净现值增幅44.77%。
2.3 连通性参数优化求解
3 生产优化

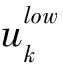
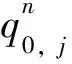
4 矿场应用
4.1 井间连通性模型

4.2 生产方案优化

5 结论
