基于LS-PrePost的不同形状装药爆炸仿真研究
2023-02-21应迪通张彦春
应迪通,张彦春
(中国刑事警察学院,沈阳 110854)
全球恐怖活动频发,涉爆案件时有发生。侦查人员在面对复杂的爆炸案件现场时,应当具备优秀的爆炸现场分析能力。爆炸现场分析是基于爆炸案件现场、爆炸试验以及爆炸仿真的理论方法。由于爆炸试验成本高、周期长、危险度高,而使用计算软件模拟爆炸过程,可以形象地展示结构的破坏和变形规律,因此爆炸有限元仿真成为了相关学者的研究重心。
爆炸有限元仿真常使用ANSYS/LS-DYNA和LS-PrePost软件进行操作。使用ANSYS/LS-DYNA 8.1进行实体建模的思路与AutoCAD相似,先构建炸药的几何体模型和空气的立方体模型,通过布尔操作和转换工作平面的多次切割,方能构建出完整的炸药模型[1]。若使用LS-PrePost进行建模,过程相对而言会简洁一些。以建立球形装药在无限空域内爆炸的1/8模型为例,选择Solid栏中的Box功能,输入参数建立立方体模型,接着使用Sphere功能直接建立1/8球体,最后使用Boolean功能切割模型即可。方形、柱形装药的几何模型同样适用此方法。划分网格常用的做法是使用Tetrahedron Mesher功能,在mesh model栏目中选择Pick skin Geometry,设定好合适的Edge Size,选定目标几何体后点击Tria Mesh使几何体表面壳单元划分完毕,点下方TetMesh完成实体有限元模型的划分。随后合并炸药模型和空气模型的共节点,以满足流体欧拉算法。上述方法属于自由网格划分方法,操作简单,适用于立方体的炸药模型,而对于球形、柱形装药的有限元模型网格划分却不容易得到优质的网格[2]。
由于方形装药的建模操作简单、网格质量高,当需要降低建模成本,又对仿真结果精度要求不高时,实际的仿真工作常常会将球形装药或者圆柱形装药简化为立方体模型。然而在大部分爆炸案件中,犯罪嫌疑人往往采用的是近似球形装药、近似柱形装药,甚至是不规则形状的炸药。在进行爆炸仿真时使用的装药形状应尽量与实际装药形状保持一致,否则会降低爆炸仿真结果的准确度。为解决球形装药建模过程中凸显的问题,本文将在第一部分专门研究球形装药建模方法,再以爆炸仿真中装药形状过度简化的问题为出发点,基于LS-PrePost软件研究不同形状装药所产生爆炸空气冲击波的差异。该项研究具有一定的理论意义,对涉爆案件的侦破具有重要的实际应用价值。
1 球形装药建模方法
查阅资料后发现,基于ANSYS/LS-DYNA和LS-PrePost软件对球形装药进行建模的有多种方法,除使用ANSYS/LS-DYNA和LS-PrePost软件的基础建模功能以外有以下三种:1)使用关键字*LOAD_BLAST建模。2)使用SPH方法建模。3)使用关键字*INITIAL_VOLUME_FRACTION_GEOMETRY建模。
本文通过总结文献资料和进行实际建模操作的方式研究三种球形装药建模方法,分析比较了三种方法在操作方法、计算时间和适用场景应用上的优缺点。
1.1 使用关键字*LOAD_BLAST建模
LS-DYNA 中储存的TNT空中爆炸超压实验数据可以利用关键字按以下方法直接调用。首先采用*LOAD_BLAST_ENHANCED关键字定义TNT当量、爆炸点及爆炸类型,再结合关键字*LOAD_SEGMENT与*LOAD_BLAST_ SEGMENT_SET定义爆炸波的接触面。此方法不需要建立空气与炸药的数值分析模型,施加方法简单,且能满足大部分爆炸案件现场的要求。
此种建模方法借用了CONWEP模型,它考虑了空气的可压缩性与轻质的特点,忽略了空气的刚度与惯性效应,因此使用它进行空中爆炸分析时不用为空气介质建模,也就是不用考虑爆炸空气冲击波在空气中的传播过程,仅有结构模型参与爆炸响应计算就可以,这样在较高的精度范围内,相比于ALE方法来说大大节省了爆炸分析的计算量[3]。此方法适用于远距离爆炸场景中玻璃介质在爆炸冲击下的动力响应研究,例如张文岚等使用了CONWEP计算模型方法对爆炸荷载作用下的高速列车车窗玻璃进行了动态响应研究[4]。
1.2 使用SPH方法建模
SPH(smoothed particle hydrodynamics)全称光滑粒子流体动力学方法,是一种无网格的纯Lagrange方法,与有限元法、有限差分法等基于网格的数值方法不同,它用一系列随机分布的粒子质点来代表整个连续介质流体[5]。这些离散出来的光滑粒子承载着所有的力学量,也能够表示材料,并确保了描述材料物理行为的状态方程能够进行有效和稳定的模拟。不同材料的粒子相对运动便形成界面滑移,且这些粒子能够按照计算公式任意流动,克服了许多基于网格的方法在求解过程中存在的问题,从而比较自然地模拟高速碰撞等物理现象[6]。在研究炸药爆炸及其作用规律的工作中,SPH方法不失为一种科学有效的方法。
建立SPH模型十分简单,在LS-PrePost的Mesh界面选择SPH Generation功能,输入球心坐标、半径、粒子分布密度即可,不需要建立空气模型;或者使用Shape Mesher事先建好实体模型,再通过SPH Generation将实体模型转化为SPH模型。具体操作的参数选择和设置如图1所示。
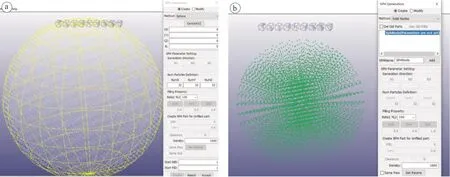
图1 建立SPH模型(a:直接建立SPH模型;b:将实体模型转换为SPH模型)Fig.1 SPH modeling (a: direct modeling; b: one converted from an ontic model)
1.3 使用关键字*INITIAL_VOLUME_FRACTION_GEOMETRY建模
此方法在传统方法基础上有所改善,是一种全新的爆炸载荷施加方式,该方法首先需要定义炸药、空气的材料参数与状态方程;然后借助关键字*ALE_MUTI-MATERIAL_GROUP定义一个包含炸药与空气的材料组;最后借助关键字*INITIAL_VOLUME_FRACTION_GEOMTRY进行填充。在LS-DYNA关键字手册中详细记载了关键字*INITIAL_VOLUME_FRACTION_GEOMTRY的用法,现以如何施加球形爆炸载荷为例介绍此方法。
图2中所建模型为1 m×1 m×1 m的立方体空气与半径5.305 cm的球形炸药,当采用传统建模时需分别单独建立空气与炸药的网格,而采用该方法建模时仅需要建立空气网格作为背景网格,然后利用关键字*INITIAL_VOLUME_FRACTION_GEOMETRY在指定区域将炸药材料填充至建好的空气网格中,并且不要求空气网格和炸药网格共节点。操作完成后,在炸药几何模型所占据的空间中,原网格中的空气被炸药材料所替代。需要注意的是,无论所选择的填充形状是什么,最终的被填充区域是炸药模型与空气模型相交的区域,即图中的1/8球体。
关键字*INITIAL_VOLUME_FRACTION_GEOMETRY的定义如图2所示,共3行。第1行的4个关键字定义空气背景,其中FMSID表示空气的PART号,FMIDITYP表示PART类型,BAMMG表示空气材料在材料组中的编号,NTRACE表示填充采样点数量,常用默认值。第2行的3个关键字定义炸药,其中CONTTYP表示炸药的形状,“6”为球形(通过选取不同的编号可模拟不同的形状,例如通过编号“5”可以定义长方体或立方体装药),FILLOPT表示填充方式,“0”表示内部填充,FAMMG表示炸药材料在材料组中的编号。第3行定义炸药的具体位置和形体参数,其中 XC、YC、ZC表示炸药球心坐标,RADIUS表示球体半径,即装药量的大小;参数设置完毕后点击右侧Insert按钮,并点击上方Accept保存。图中亮黄色网状球体即为建立的球形装药示意图。
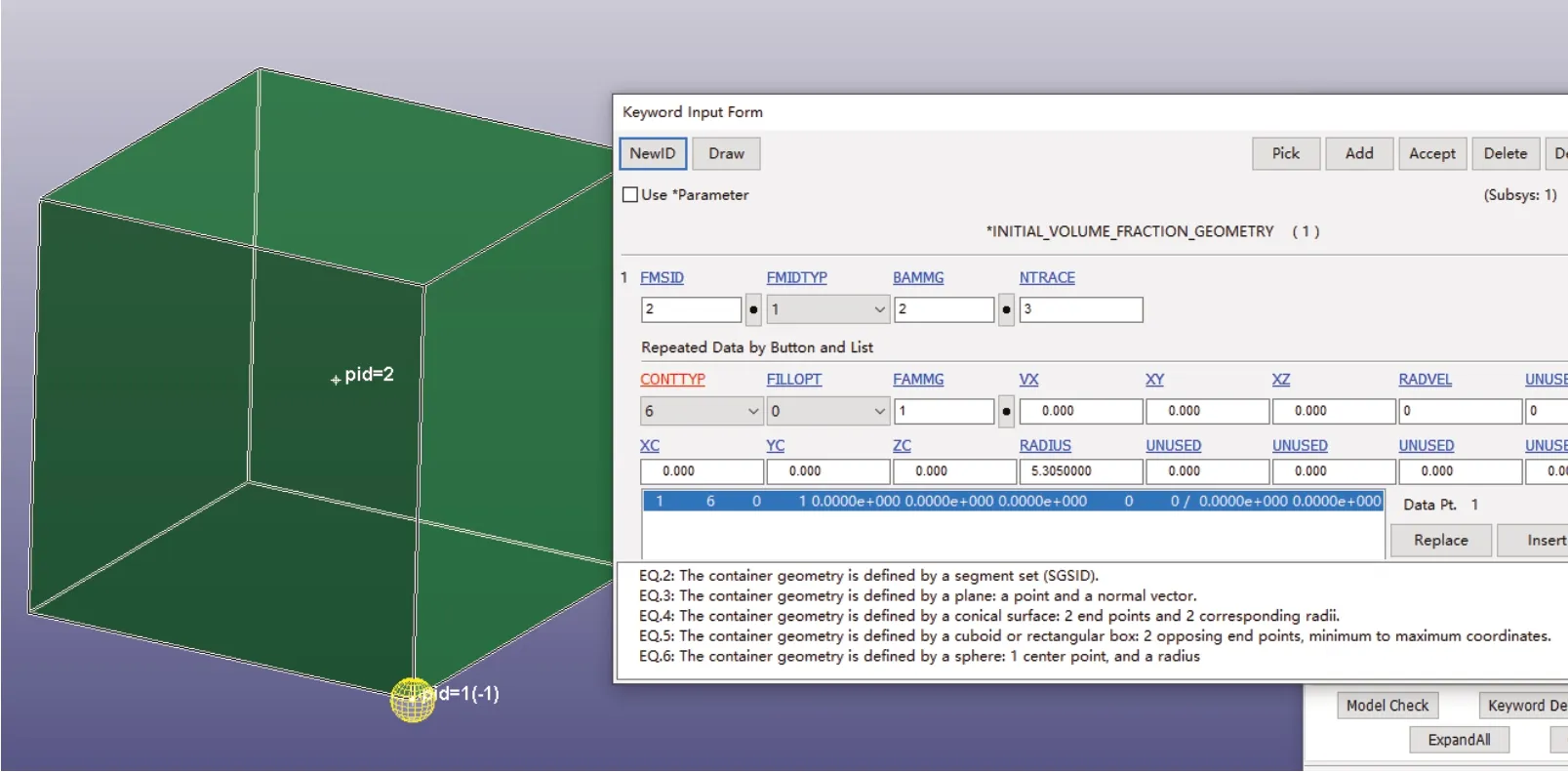
图2 使用关键字*INITIAL_VOLUME_FRACTION_GEOMETRY建模Fig.2 Modeling with the keyword *INITIAL_VOLUME_FRACTION_GEOMETRY-led way
1.4 不同建模方法优缺点
使用关键字*LOAD_BLAST建模具有局限性,其可供选择的爆炸类型只有表面接触爆炸和空中爆炸,装药的形状只有球形或半球形,且不能对表面形状复杂或有遮挡的考察对象进行动力分析。需要注意的是,在近爆情况下,该方法所调用的经验公式精确度并不高。因此在满足以下三种爆炸条件的情况下使用关键字*LOAD_BLAST建模会更有优势:1)球形装药;2)远距离爆炸;3)爆炸波接触表面几何结构简单。而使用SPH方法的优点是无需网格,没有网格畸变问题,形成的爆轰效果相对而言更加逼真,可以形象地模拟炸药爆轰及产物膨胀飞散过程。在使用SPH方法时,由于FEM算法和SPH算法各自存在缺陷,通常会结合Lagrange和SPH算法,即SPH-FEM耦合法。一部分学者[7-9]认为该方法可避免FEM算法的网格畸变问题,同时在重点部位发挥SPH算法优势,可以大大减少计算时间。
使用关键字* INITIAL_VOLUME_FRACTION_GEOMETRY建模则不需要单独建立炸药单元,仅仅通过关键字修改相应参数,就可以建立不同形状的模型、快速改变装药量,操作灵活,减少了重复建模的繁琐过程,也能避免复杂模型划分网格的困难。
2 不同形状装药形成的爆炸空气冲击波
在各种爆炸场景中,不同的物理参数直接对爆炸空气冲击波的超压峰值造成影响,例如装药形状、炸药密度、起爆点的空间位置、炸药的湿度、环境温度等参数。本文尝试将装药形状参数与爆炸空气冲击波响应值联系起来,使用上文提到的不同形状装药建模方法进行爆炸仿真实验,研究不同形状装药爆炸所形成的空气冲击波超压。考虑到使用关键字* INITIAL_ VOLUME_FRACTION_GEOMETRY可以在不需要重新建模的情况下快速建立不同形状装药的有限元模型,本文将使用该方法建立爆炸仿真模型,研究不同形状装药在无限空气域中的爆炸。
2.1 构建空中爆炸有限元模型
为了模拟真实爆炸案件中常见的近距离爆炸,本次爆炸仿真的测试点在0~1 m之间。爆炸仿真实验采用cm-g-µs单位制,使用LS-PrePost进行前后处理,使用ANSYSLS-DYNA求解器进行计算。TNT炸药当量定为1 000 g,密度是1.6 kg/cm3。通过关键字分别建立球形、柱形和方形装药。其中球形装药半径为5.305 cm;为了使柱形装药尽量接近球体,设定圆柱体长径比为1,直径和高均为9.260 cm;方形装药边长为8.550 cm。
三种装药均设置为中心点起爆。使用Shape Mesher功能建立100 cm×100 cm×100 cm的立方体空气模型,单元划分尺寸为1 cm;采用SOLID164单元和欧拉算法。划分立方体单元共1 000 000个;三种工况的炸药模型分别通过关键字*INITIAL_VOLUME_FRACTION_GEOMETRY建立。考虑到此次爆炸仿真的对称性,取八分之一实体进行建模,从而减少计算量。
2.2 材料参数选择
2.2.1 TNT本构模型和状态方程参数
TNT炸药采用目前比较通用的HIGH_EXPLOSIVE_BURN模型以及JWL状态方程加以描述,相关参数如表1所示[10]。
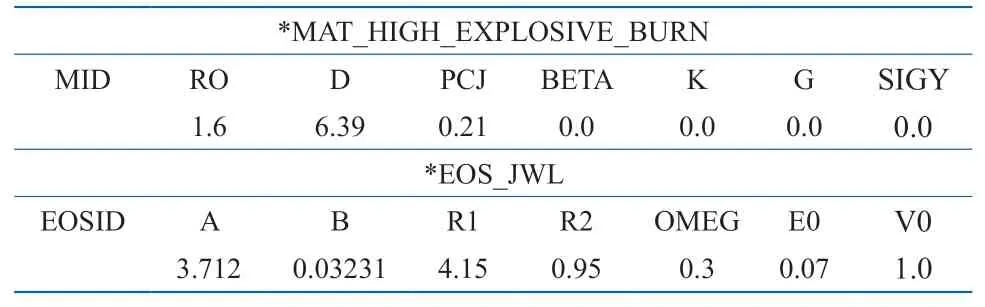
表1 炸药材料参数Table 1 Parameters for explosive as material
2.2.2 空气本构模型和状态方程参数
空气采用NULL材料模型以及LINEAR_POLYNOMIAL状态方程加以描述,在数值分析中假设标准大气条件,即平均海平面和标准温度为15 ℃,大气压力为101.325 kPa[11],相关参数如表2所示[10]。

表2 空气材料参数Table 2 Parameters of air as material
2.3 无限空气域中爆炸过程的仿真
无限空气域中的爆炸是炸药在空气中爆炸的一种理想模型,可以使用此模型的仿真结果与空气中炸药爆炸的过程做对比。炸药在空气中爆炸会瞬时转变为高温高压的爆炸产物,爆炸产物在空气中进行膨胀,其结果是在爆炸产物内形成稀疏波。同时,爆炸产物强烈压缩空气,在空气中形成爆炸空气冲击波[12]。
通过仿真手段可以将空中爆炸过程准确形象地展现出来,图3是1 kg球形TNT爆炸后在不同时刻的压强等值面效果图,以压力云图的方式表现了爆炸空气冲击波的传播过程。如图所示,爆炸空气冲击波从起爆中心开始,以球形曲面的传播方式向外围传播。爆炸空气冲击波伴随着传播距离的增加能量逐步耗散,在爆炸传播的初始阶段,超压峰值急速衰减,而后衰减过程较为平缓。其原因是在总能量不变的情况下,波阵面的表面积急速扩大,通过单位面积的能量就急剧减小;另一方面是空气受到了绝热压缩使得温度瞬间升高,产生了不可逆的能量损失,消耗了部分能量[13]。
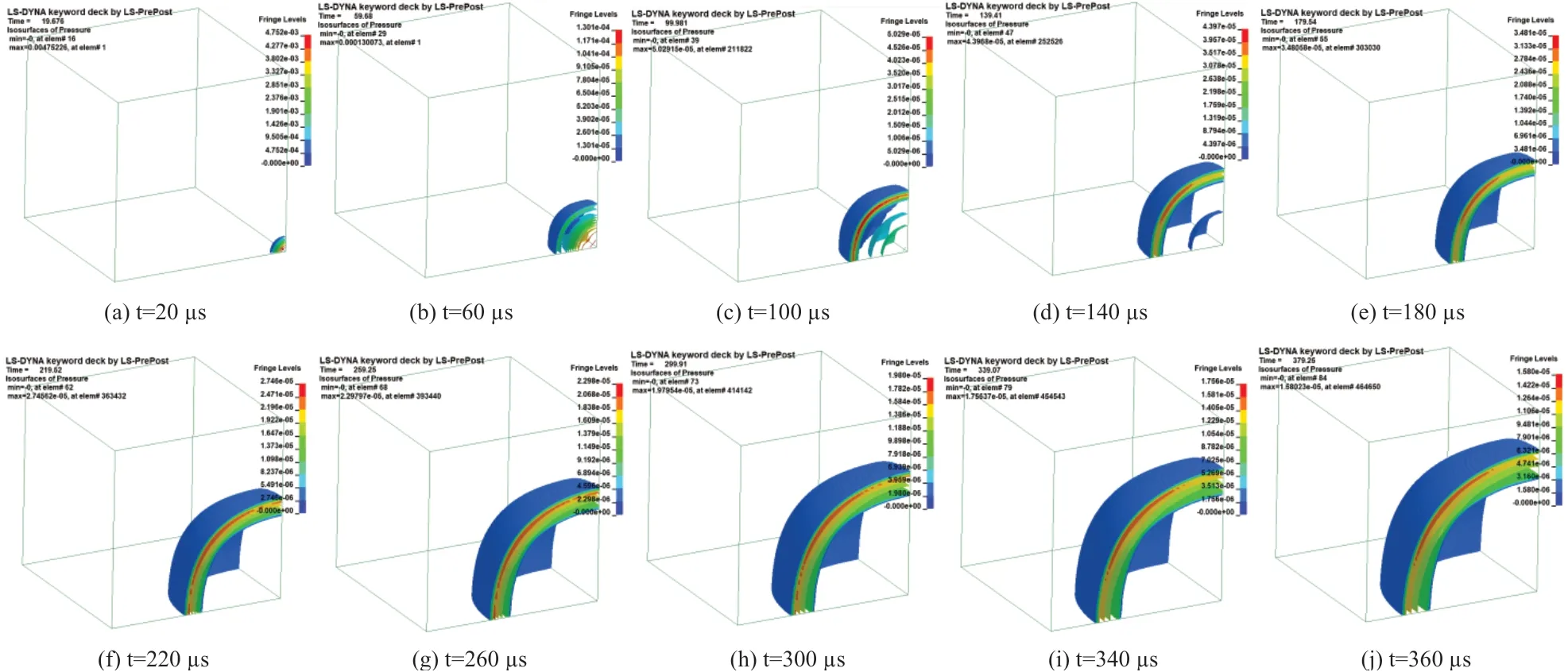
图3 球形装药爆炸空气冲击波在不同时刻的压强等值面图Fig.3 The moment-different pressure-equivalent surfaces from the exploding air-shock waves with spherical charging
2.4 有限元模型验证
为验证此基础模型是否符合爆炸空气冲击波在自由空气中的传播规律,本文将基础模型的仿真结果与经验公式预测值进行对比。常用来预测爆炸空气冲击波超压值的经验公式有两种:TM5-1300手册数据拟合公式和Henrych J公式,这两种公式在国际上受到广泛认可,近爆区的准确性相对较高。
表3和图4显示了基础模型仿真结果与经验公式计算结果的对比情况,图4中仿真的结果和经验公式的整体趋势较为一致,结合图3中爆炸空气冲击波阵面的传播形态,可以得知此模型符合爆炸空气冲击波的传播规律。

图4 爆炸仿真结果与经验公式计算结果对比Fig.4 Comparison of the results from simulative explosion with those from the empirical equation’s calculation
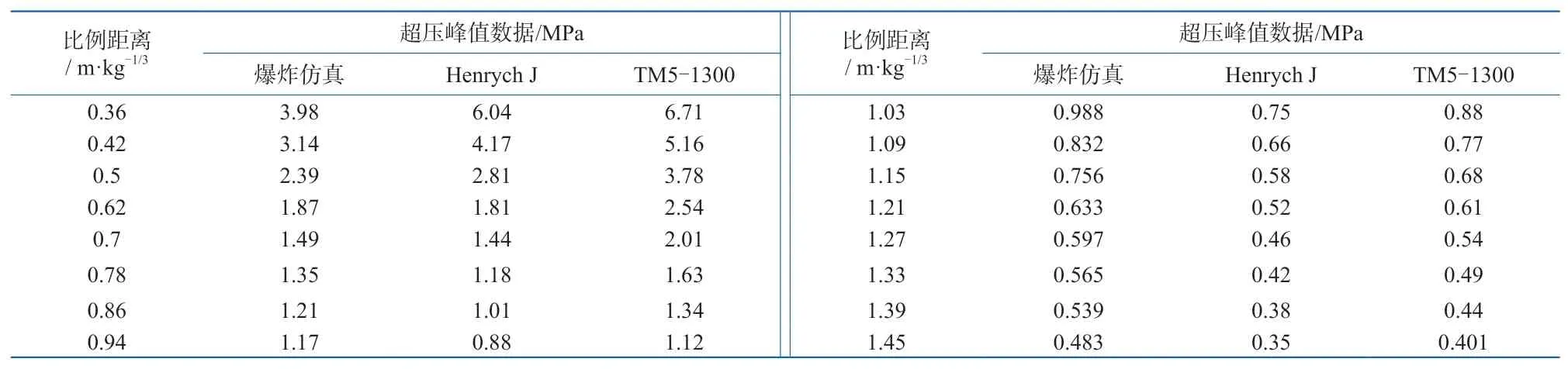
表3 爆炸仿真结果与经验公式计算结果对比Table 3 Comparison of results from numerical simulative explosion with those from empirical equation’s calculation
从图4中还可以看出,仿真结果相对偏小,尤其是在比例距离小于0.5 m·kg-1/3时,仿真结果小于经验公式的计算值。其原因之一可能是爆炸的强瞬时性以及实验装置的采样频率等受到限制,使得各种实验结果的精确数据很难在实验中被测得,所获取的数据存在很大的离散性,原因之二是仿真建模难以完全还原采集实验数据的真实爆炸场景,设备之间或者地面墙体间的反射波会增强爆炸空气冲击波的威力。
由表3和图4可见,爆炸仿真的超压峰值数据随着比例距离的增大而越来越接近经验公式的数据,且变化趋势与Henrych J公式、TM5-1300手册数据拟合公式均一致,特别是数值仿真结果与Henrych J公式结果非常接近,由此说明,本文建立的爆炸数值仿真模型是有效可靠的。
2.5 爆炸仿真结果及分析
在经过验证的有限元模型基础上,采用控制变量的方法改变爆源形状参数,使用ANSYSLS-DYNA求解器依次对球形、柱形、方形装药的有限元爆炸模型进行求解,得到不同比例距离下的超压峰值以及相对应的超压峰值到达时间,选取部分有代表性的爆炸仿真结果,作图5来展示三种不同装药方式在各比例距离处的超压峰值对比情况;分析柱形和方形装药相对于球形装药的差值,结果如表4所示。

图5 三种装药方式在不同比例距离处的超压峰值对比图Fig.5 Comparison among the three charging ways about their peak overpressures at different scaling distances

表4 三种装药方式分别在不同比例距离处的超压峰值及其差值Table 4 Peak overpressures and differences at diverse scaling distances from the indicated three charging ways
爆炸仿真结果表明:1 kg TNT空中爆炸时,选择0.1、0.4、0.6、1.0 m·kg-1/3距离处作为四个观测点,柱形装药与球形装药的超压峰值比值分别为:1.44、1.51、1.496、1.44,差值分别为9、1.73、0.93、0.50 MPa;而方形装药与球形装药的超压峰值比值分别为:1.66、2.08、2.29、2.89,差值分别为13.40、3.63、2.41、2.14 MPa。可见,在比例距离小于等于1.0 m·kg-1/3时,柱形装药的超压峰值与球形装药更接近,而方形装药超压峰值与球形装药差异更大;随着比例距离的增加,柱形装药的峰值超压与球形装药的比值变化不大,而方形装药的峰值超压与球形装药的比值逐渐增加,变化较大。
3 结论
本文基于LS-PrePost软件,研究了使用关键字*LOAD_BLAST建模、SPH法建模以及关键字*INITIAL_VOLUME_ FRACTION_GEOMTRY建模等三种常见建模方法的优缺点和适用场景,利用关键字*INITIAL_VOLUME_FRACTION _GEOMTRY建模方法,建立了球形装药有限元模型,研究得到了1 kg TNT在不同装药形状下,爆炸产生的空气冲击波超压的不同。研究表明,不同装药形状对于爆炸产生的冲击波超压的影响是不容忽视的。在研究实际爆炸案件的装药及其爆炸破坏作用时,应尽可能采用最接近实际情况的装药形状,在通过爆炸仿真方法研究问题时,也要选择合适的建模方法和装药条件,才能保证分析结果的准确可靠。
