基于灰色神经网络的小样本纳米TiO2改性聚酰亚胺薄膜寿命评估
2023-02-21刘道生陈亦杰
刘道生, 陈亦杰, 张 良
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
0 引 言
聚酰亚胺(PI)薄膜是电气领域中重要的绝缘材料之一,其凭借出色的性能,广泛应用在电工绝缘、柔性显示、航空航天以及5G通信等领域[1-2]。纳米粒子改性PI薄膜的可靠性随着制备工艺进步、介电性能调控技术发展得到提高[3-5],导致其寿命试验时间延长、试验成本增加和失效数据少等问题,使得基于大样本容量的传统绝缘寿命评估方法解决小样本数据的绝缘寿命评估问题存在局限性。因此,有必要研究能够在小样本容量下准确评估纳米粒子改性PI薄膜寿命的方法。
文献[6]假设电缆的先验分布是Weibull比例风险分布,运用贝叶斯推断提出不同工况下小样本容量电缆个体的可靠性评估方法。贝叶斯方法不依赖样本数量,使用少量数据和先验信息可以得到较好的估计,但假设的先验信息不同会产生不同的评估结果,导致评估中存在主观误差。受PI薄膜运行的特殊性影响,其先验信息较少,因此使用贝叶斯推断评估PI薄膜可靠性存在较大的主观不确定性。文献[7]采用Bootstrap方法扩充绝缘样本容量,建立非恒定形状参数的寿命评估模型,但Bootstrap方法得到的分布参数估计结果偏移大,且过分依赖原始样本的数据质量。文献[8]指出基于Bootstrap方法的寿命评估结果可能不准确。文献[9]以平均电荷密度作为退化特征量,选取Weibull分布作为伪失效寿命分布,利用虚拟增广法对绝缘可靠性进行评估。虚拟增广法的准确性取决于伪失效寿命数据分布模型能否客观表征绝缘寿命实际的概率分布。文献[10]通过蒙特卡罗仿真比较不同参数估计方法、样本容量等确定最佳的绝缘直流耐压寿命评估方案。但蒙特卡罗算法需已知绝缘寿命概率密度分布函数,因此蒙特卡罗依赖绝缘寿命分布形式和参数特征的准确性,且无通解公式。文献[11]通过支持向量机(SVM)和网格搜索法对原始数据进行训练,预测得到服从原始样本失效规律的大样本容量数据,表现出优秀的学习性能。SVM方法通过原始样本训练得到惩罚因子、核函数参数以及不敏感系数等模型参数,基于训练后的SVM模型扩充样本容量。但野值点、数据序列波动程度对SVM方法影响较大,单纯使用SVM难以保证模型参数的准确性。神经网络的输入是原始样本或对原始样本进行处理后得到的数据特征量,训练并保存网络的结构与参数,输出与原始数据具备相同特性的大样本数据。文献[12]针对小样本失效数据,使用BP神经网络对扩充后的数据进行可靠性分析,发现预测结果与实际情况之间具有较好的一致性。神经网络完全不需要先验信息,也不需要假设失效数据的分布模型,有助于降低其他小样本容量寿命评估方法的误差。
综上,本文针对纳米TiO2改性PI薄膜寿命试验成本高、失效数据少等特点,提出基于灰色神经网络的样本扩充寿命评估方法。将4种经验累计失效概率公式计算得到的失效率作为灰色神经网络输入,输出是改性PI薄膜失效时间,分别对不同电压下灰色神经网络进行自主学习训练,通过训练后具有相同结构参数的模型对相应电压下的样本数量进行仿真扩容,得到与原始数据特征和变化规律相似的扩容数据。最后,利用扩容前后的数据分别在对数正态分布和Weibull分布下,采用最小二乘法得到不同电寿命评估模型的结果并进行比较。
1 试 验
1.1 主要原材料
纳米TiO2颗粒,粒径为20 nm,南京海泰纳米材料有限公司;二甲基乙酰胺(DMAC),浓度≥99.8%,Mackin公司;4,4-二氨基二苯醚(ODA),浓度≥98.0%,Aladdin公司;吡喃二酸酐(PMDA),浓度≥98.5%,Aladdin公司。
1.2 样品制备
采用原位聚合法制备纳米TiO2改性PI薄膜,制备步骤见图1。在圆底烧瓶中加入纳米TiO2颗粒和二甲基乙酰胺(DMAC)溶液,用搅拌器搅拌1.5 h,获得分散均匀的悬浊液。向烧瓶中加入提前在真空干燥箱中干燥3 h的4,4'-二氨基二苯醚(ODA),利用超声波振荡溶液30 min,直到ODA完全溶解。然后,将同样干燥完成的吡喃二酸酐(PMDA)分成5份依次缓慢的倒入悬浊液中,ODA和PMDA的质量比为1∶1.05。在PMDA完全溶解后,用搅拌器搅拌混合物1 h,将其浇铸在涂有中性脱模剂的定制玻璃板上。将玻璃板放入真空干燥箱中干燥2 h。最后将样品放入烘箱中,分别在100、140、180、220、260℃下进行梯度固化1 h,从玻璃板上剥离得到厚度为(25±1)μm的纳米TiO2改性PI薄膜。
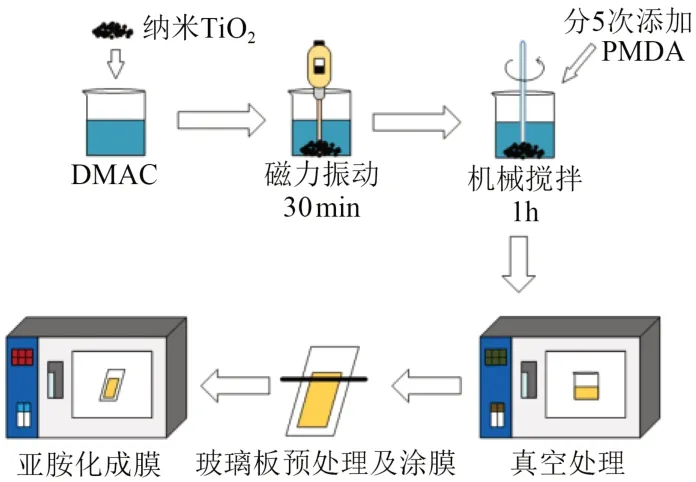
图1 纳米TiO2改性PI薄膜制备流程图Fig.1 Preparation flow chart of PI film modified by nano TiO2
1.3 电寿命试验
把采用相同工艺制备得到的性能差别微小的同批次32个改性PI薄膜分为4组,每组8个样品,再将4组样品分别在800、900、1 000、1 100 V下进行电老化试验;使用柱板电极,电极间隙为13 mm,试验温度为80℃,电压频率为2 kHz,得到不同电压下试样的失效时间,如表1所示。
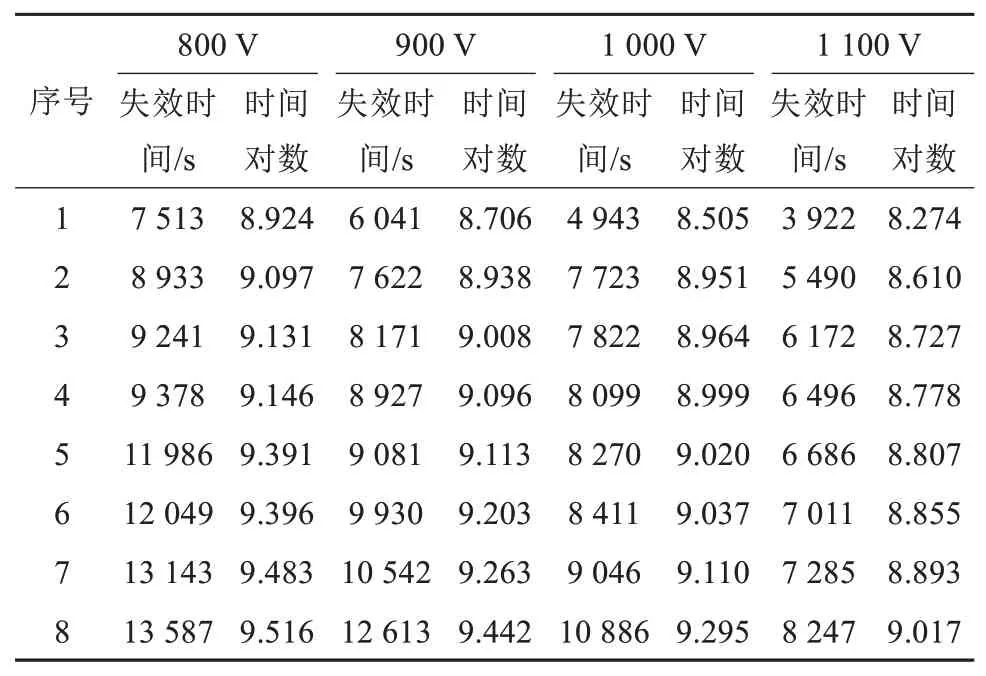
表1 不同电压下的失效时间Tab.1 Failure time under different voltages
1.4 电老化寿命评估模型
纳米TiO2改性PI的电老化寿命L与外施电压U存在符合反幂函数模型(IPM)的经验关系式,如式(1)[13]所示。

式(1)中:L为样品在试验电压下的失效时间,s;U为施加在样品上的试验电压,kV;n是绝缘的寿命表征指数,其值越大说明绝缘寿命越长;a是与材料性能相关的常数。
2 纳米TiO2改性PI薄膜寿命分布模型
对数正态分布和Weibull分布是绝缘寿命评估中常用的概率分布,本文将分别在对数正态分布和Weibull分布下,使用原始失效数据和样本容量扩充后的数据,对纳米TiO2改性PI薄膜进行电老化寿命评估,并比较评估结果。
2.1 对数正态分布
当纳米TiO2改性PI薄膜的电寿命数据服从对数正态概率模型时,其寿命的概率分布函数和密度函数分别如式(2)和式(3)所示。
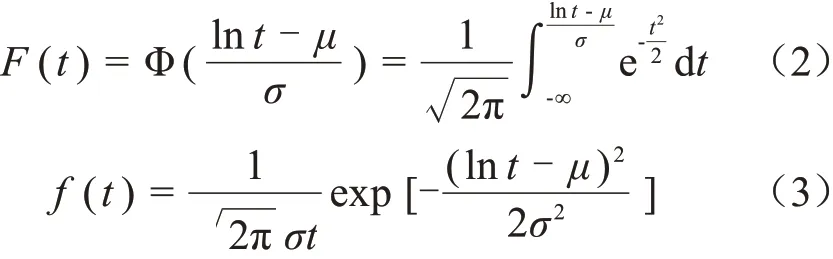
式(2)~(3)中:Φ(x)是标准正态分布函数;t是试样的失效时间;μ、σ分别是对数正态分布的数学期望和标准差。
对式(2)进行整理,得到式(4)。
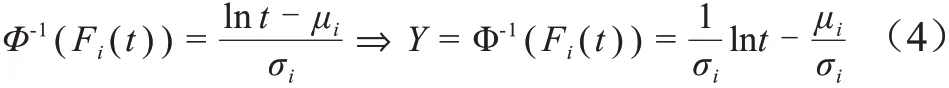
2.2 Weibull分布
当纳米TiO2改性PI薄膜的电寿命数据服从Weibull概率模型时,其寿命的概率分布函数如式(5)所示。
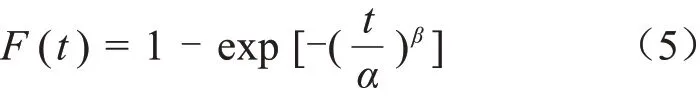
对式(5)求导可得密度函数式(6)。
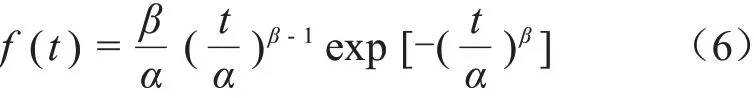
对式(6)取两次对数运算可得式(7)。
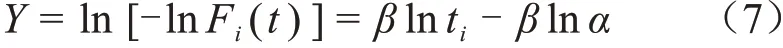
式(7)中:Fi(t)为累计失效概率;t为试样失效时间;α为尺度参数;β为形状参数。
在绝缘寿命评估中,采用不同的绝缘失效概率分布形式、寿命评估模型和经验累计函数等将得到不同的参数估计结果,最终影响绝缘统计寿命的准确性[14-15],因此避免人为选择带来的主观误差是十分必要的。大量精确的失效数据是绝缘寿命评估结果准确可靠的前提,但随着PI薄膜纳米调控技术、制备工艺和生产成本等提高,采集大量失效数据已成为难题,小样本失效数据寿命评估问题更为常见。
由于小样本数据统计特征不显著,可能导致多种分布模型拟合效果良好且相似[16],从而不能准确反映纳米TiO2改性PI薄膜的实际失效进程,也不能表征其实际失效特性。本研究运用最小二乘法拟合扩充前后的失效数据,通过相关系数对比和确定纳米TiO2改性PI薄膜寿命评估的最佳方案。
3 灰色神经网络模型
3.1 灰色神经网络模型建立
小样本扩容的实质是选取合适的方法,挖掘有限信息量中的潜在信息,找出并运用信息之间的变化规律进行准确预测。
神经网络预测精度高,具备良好的非线性函数逼近能力,可以揭示绝缘失效进程的发展趋势。而灰色模型针对小样本、贫信息的原始数据,通过对“部分”原始数据进行生成、挖掘,建立微分方程,从而预测未来数据[17]。本文将两者相结合对纳米TiO2改性PI薄膜的小样本失效数据进行数据扩充,不仅可以表征纳米TiO2改性PI薄膜失效数据的整体变化规律,还无需假设原始数据的分布模型,减小主观误差。
为弱化纳米TiO2改性PI薄膜原始失效数据序列的离散性,灰色理论通过正向累加序列生成法,得到规律性强、随机性弱的新数列x(1)(k),设原始失效序列为x(0)(k)(k=1,2,...,N),如式(8)所示。
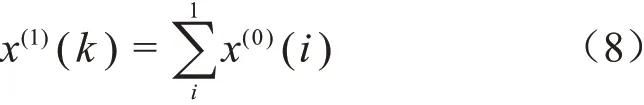
式(8)中:k=1,2,…,N,N是单一电压水平下失效数据的个数。
建立x(1)(k)的微分方程为式(9)。
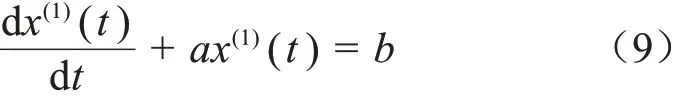
求解式(9)对应的离散时间序列响应函数得到式(10)。
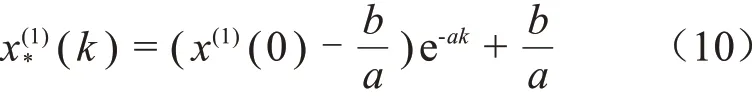
整理式(10)得到式(11)。
将式(11)引入BP神经网络中,得到1个输出参数、n个输入参数的灰色神经网络模型,图2是其网络拓扑结构。
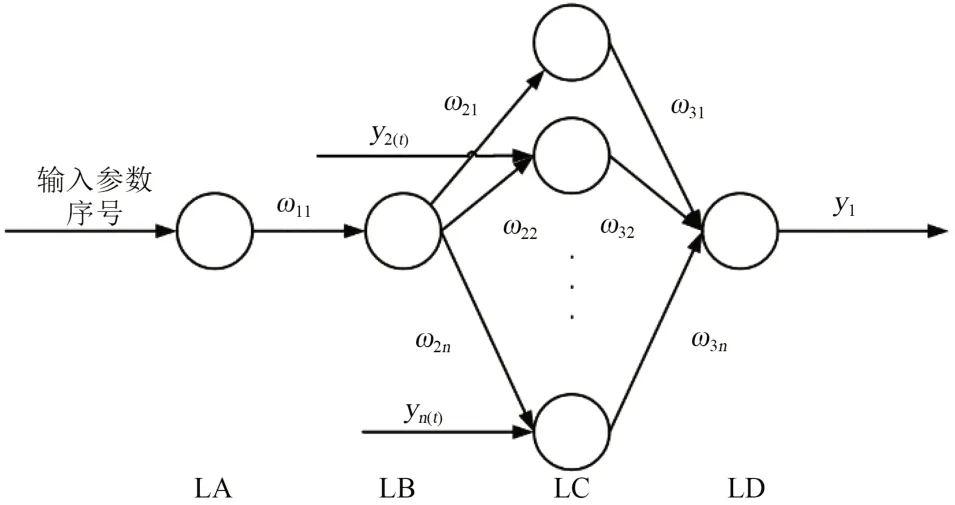
图2 灰色神经网络的拓扑结构示意图Fig.2 Structure of Grey neural networks model
图2中:y2(t),...,yn(t)是网络的输入参数;ω11,ω21,ω22,...,ω2n,ω31,ω32,...,ω3n是网络权值,y1是输出值;LA、LB、LC、LD分别为神经网络的4层。
令2b1/a=u1,2b2/a=u2,…,2bn-1/a=un-1,初始权值可转化为:ω11=a,ω21=y1(0),ω22=u1,ω23=u2,…,ω2n=un-1,ω31=ω32=…=ω3n=1+e-at。则L4层输出节点阈值为θ=(1+e-at)(d-y1(0))。
首先通过灰色方法对原始数据进行预测,将原始值和预测值作为输入对神经网络进行训练,修正灰色神经网络预测的误差。通过对累加生成的新失效寿命序列进行误差修正,降低了原始序列的分散性,进而突出失效数据的变化规律。
3.2 基于灰色神经网络的样本扩充
在不确定改性PI薄膜寿命分布模型时,可用多种经验累计失效概率作为灰色神经网络的输入,降低累计失效函数主观选择造成的误差。
数学期望公式为式(12)。
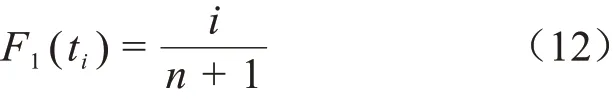
中值公式为式(13)。
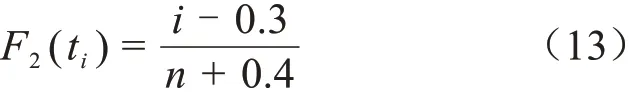
Blom公式为式(14)。
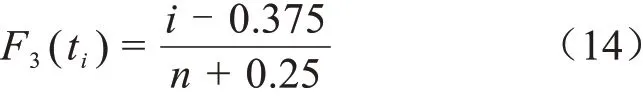
海森公式为式(15)。
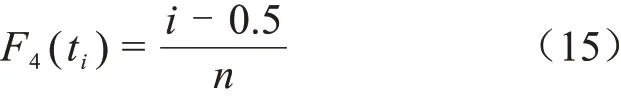
式(12)和式(13)都是通过Fi的特征值进行估计,式(12)结构简单且不受分布形式影响;式(13)是F̂i中值近似公式;式(14)是通过xi的特征值进行估计,由正态分布推导得到的近似公式;式(15)是古典概率公式的修正式,适合对偏态系数为正的分布。式(12)~(15)有一定理论基础或来自工程经验,需要确定最适合纳米TiO2改性PI薄膜寿命评估的经验公式,降低评估中的误差,以提高评估结果的准确性。
根据图3所示基于灰色神经网络的纳米TiO2改性PI薄膜寿命评估后流程,将得到的纳米TiO2改性PI薄膜电老化试验的失效数据,通过上述的累计失效概率公式计算出相应的失效概率值Fi,把向量{F1,F2,...,FN}作为灰色神经网络的输入,把原始失效序列{t1,t2,...,tN}作为灰色神经网络的输出,对灰色神经网络进行学习训练,以优化确定网络内部的权参数和阈值参数,并应用该网络模拟生成新的失效数据。
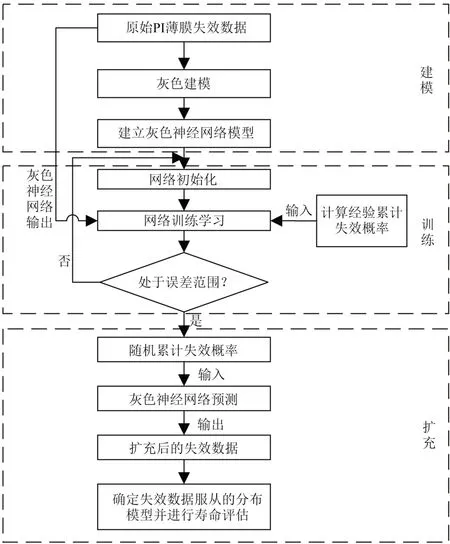
图3 基于灰色神经网络的纳米TiO2改性PI薄膜寿命评估流程图Fig.3 Life evaluation flow chart of PI film modified by nano TiO2 based on grey neural network
灰色神经网络的特性决定其仿真生成的失效数据与原始数据有近似的规律和特性,因此可用于寿命评估。
4 实例分析
通过灰色神经网络仿真生成的扩充失效数据具备与原始失效数据相似的特征和变化规律,分别对样本量扩充前后的失效数据在Weibull分布和对数正态分布下使用数学期望公式、中值公式、Blom公式和海森公式进行纳米TiO2改性PI薄膜的寿命评估,得到不同评估方案下的参数值;根据最小二乘法的相关系数ρ确定扩充前后失效数据最佳的寿命评估方案,即ρ的绝对值越接近于1,说明该方案越能反映真实的失效进程。
将采集到的纳米TiO2改性PI薄膜失效数据按数值排序:t1≤t2≤⋅⋅⋅≤tN。灰色神经网络的输入是通过数学期望公式、中值公式、Blom公式和海森公式计算的累计失效概率向量F1(ti)、F2(ti)、F3(ti)、F4(ti),输出分别是不同电压下原始失效时间的向量T800V、T900V、T1000V、T1100V。对4个电压下的灰色神经网络进行训练,当训练误差小于0.001时,保存灰色神经网络的结构和参数。向量F1(ti)、F2(ti)、F3(ti)、F4(ti)和T800V、T900V、T1000V、T1100V分别为:
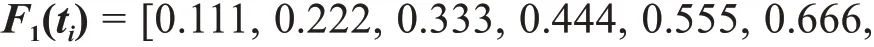

取n=50,按式(12)~(15)分别计算累计失效概率得到4×50的向量矩阵,将矩阵各行分别按从小到大排序,作为4个电压下已完成训练的灰色神经网络模型的输入,预测4个电压下失效数据样本量为50的灰色神经网络仿真扩容数据。
采用最小二乘法对扩充前后的失效数据进行拟合,得到对数正态和Weibull分布下不同经验累计失效函数的评估结果,见表2,分析拟合参数和评估结果发现:
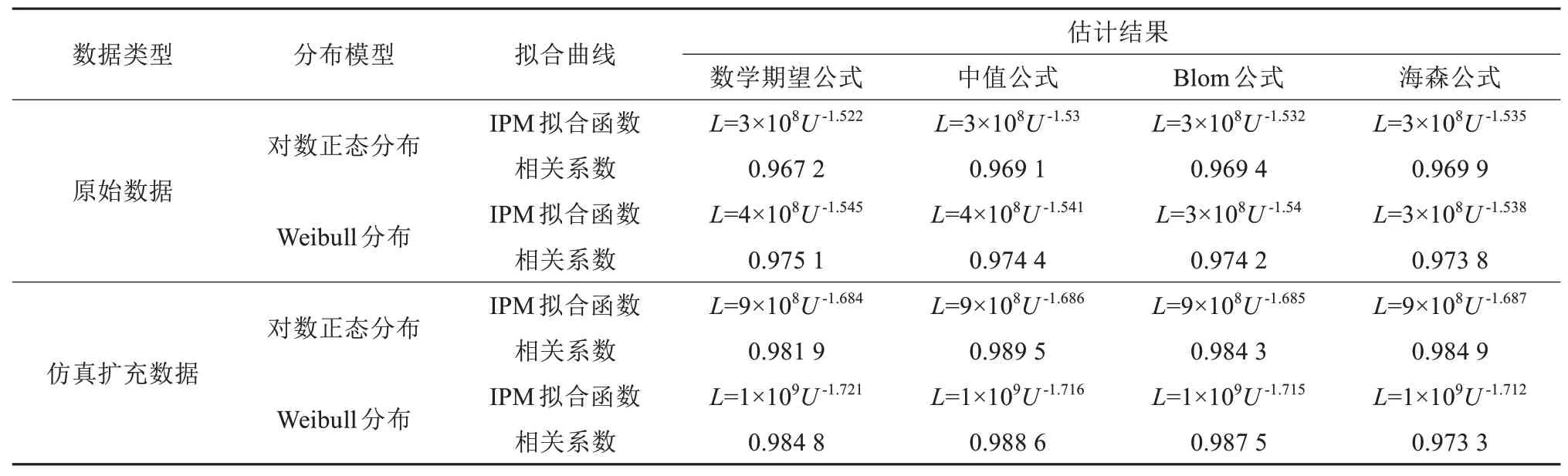
表2 纳米TiO2改性PI薄膜寿命评估结果Tab.2 Life evaluation results of PI film modified by nano TiO2
(1)相关系数ρ表征失效数据与对应概率分布的符合程度,对比Weibull分布和对数正态分布的相关系数可知,对于原始数据,在各个经验累积失效函数下Weibull分布拟合的相关系数都显著优于对数正态分布,因此Weibull分布更符合纳米TiO2改性PI薄膜原始失效数据的失效分布模型。
(2)对比扩充前后的失效数据拟合情况,发现扩充后的相关系数ρ普遍大于小样本数据,说明经灰色神经网络扩充后的寿命评估方案一方面降低了来自分布模型选择的主观性误差,另一方面减小了失效数据样本量小造成的评估误差。
(3)不同的经验累积失效函数下,两种失效概率分布模型的拟合曲线及参数略有差异,但样本容量扩充后的相关系数更接近于1,说明曲线拟合的效果得到提高,即表明随着失效样本容量的增加,经验累积失效函数对寿命评估的影响得到减弱。
5 结 论
(1)灰色神经网络的特性决定其扩充得到的失效数据与原始数据具备相似的特征和变化规律,不会改变其统计分布规律。此外,灰色神经网络还能降低失效数据分布模型选择错误造成的主观误差。
(2)选择合适的寿命评估方案,可以降低绝缘寿命评估误差。当失效数据为小容量时,纳米TiO2改性PI薄膜的电寿命评估方案应选择IPM模型、Weibull分布和数学期望公式的组合,该方案在小样本下误差最小;当失效数据为大容量时,应选择IPM模型、对数正态分布和中值公式的组合,该方案在大样本下误差最小。
(3)评估方案受样本量影响发生改变的主要原因是不同样本容量的最优拟合分布模型可能不一致,且失效数据分散性大小发生变化。样本容量扩充后的拟合相关系数比原始失效数据更接近于1,说明样本扩充后的曲线拟合效果更好,参数估计也更精确,因此寿命评估结果也更准确。
