对旋式轴流泵后置叶轮水力性能分析
2023-02-21徐添蔡一平楚士冀石丽建朱军江宇航
徐添,蔡一平,楚士冀,石丽建*,朱军,江宇航
(1. 扬州大学水利科学与工程学院,江苏 扬州 225100;2. 江苏省水利科学研究院,江苏 南京 210000;3. 国际小水电中心,浙江 杭州 310002)
近年来,轴流泵在农业灌溉、城市供水、跨流域调水等大型泵站工程方面得到广泛的应用,其典型特点是流量大、扬程低[1].而工程用泵常常需要满足大流量、高扬程的要求,此时单叶轮轴流泵就难以满足应用需求.对旋式轴流泵是一种特殊的轴流泵,它是由2个旋转方向相反的叶轮构成.对旋式叶片在直升机、通风机及潜艇的动力装置上应用成熟,对旋式轴流泵克服了双级轴流泵轴向尺寸较大的问题,但由于其结构复杂,在泵站工程较少采用.但由于其具有流量大、扬程高、运行高效区宽等特点,在工程上具有较好的应用前景,有利于推动流体机械及水利事业的进一步发展.
目前,对旋式轴流泵受到了众多国内外学者的普遍重视.王德军等[2]、孙壮壮等[3]和王俊[4]均以对旋式轴流泵为研究对象,对其内部流场进行分析,研究并总结出对旋式轴流泵拥有较为优秀水力性能的结论.孙壮壮[5]、王国玉等[6]采用数值模拟的方法研究了串列式轴流泵的内部流场,得出前、后置叶轮的水力性能明显不同.CAO等[7]研究了对旋式轴流泵后置叶轮的设计方法,考虑了后置叶轮叶尖处来流的速度缺陷,通过优化进一步提高了后置叶轮的性能.FURUKAWA等[8]对前后置叶轮进行组合试验,提出了对旋式轴流泵的运行高效区比普通轴流泵宽23%.宋娟娟[9]、幸欣等[10]和程德磊等[11]研究了改变对旋风机前后置叶轮安放角后其性能的变化,得出第二级叶轮叶片安放角的改变对运行效率的影响较大.CHOI等[12]、SHI等[13-14]基于数值模拟的方法,采用k-ε紊流模型,证明了数值模拟技术的可靠性.当前对于对旋式轴流泵的研究较少,特别是对于对旋式轴流泵后置叶轮水力性能的研究十分匮乏.
文中基于前人的研究思路,采用数值模拟和模型试验相结合的方法,研究对旋式轴流泵的水力性能,并进一步与ZML水泵模型的性能进行比较,进而研究后置叶轮对其水力性能的影响,拟为对旋式轴流泵装置的优化设计提供参考.
1 研究对象
1.1 计算模型
对旋式轴流泵模型是由进水直管、前置叶轮、后置叶轮、出水弯管这4个部分组成.其中前、后置叶轮模型均为ZML高效轴流泵模型叶轮,翼型均采用NACA06翼型.叶轮水力模型主要设计参数:设计流量Qd=360 L/s,设计扬程Hd=5.5 m,转速n=1 450 r/min,叶轮直径D=300 mm,前置叶轮叶片数为4片,后置叶轮叶片数为4片.计算模型如图1所示.
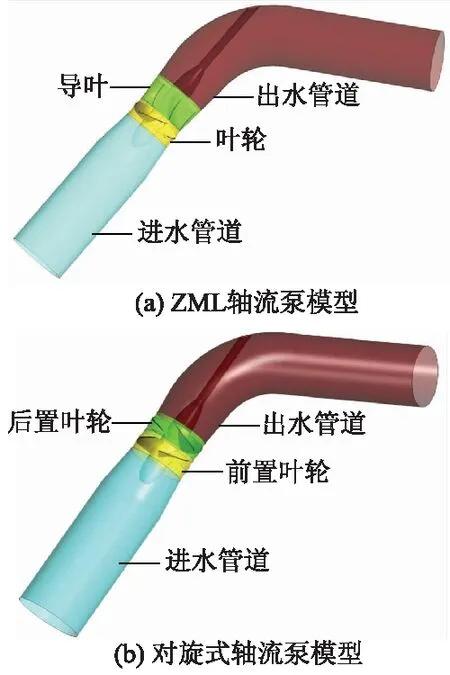
图1 泵装置模型
1.2 控制方程及边界条件
利用ANSYS CFX商业软件进行数值计算,控制方程采用雷诺时均N-S方程,紊流模型采用标准k-ε模型.标准k-ε湍流模型是在工业应用中被普遍使用的湍流模型,其计算收敛性和精确性能够符合工程计算要求.考虑到对旋式轴流泵装置内部流线并无较大弯曲,且主要预测其装置外特性,因此采用标准k-ε模型计算.最大迭代步数为1 500步,收敛精度为10-5.进口边界条件设置为总压进口,压力设为1.013×105Pa;出口边界条件设置为质量流量出流;叶轮设置为旋转域,其他区域为静止域.固体壁面边界包括叶片表面、轮毂表面、叶轮轮缘的内表面等,采用满足黏性流体的无滑移条件,近壁区采用标准壁面函数边界条件.对于静止域和旋转域及旋转域和旋转域之间的动静交界面采用Stage模型,其余各交界面均采用None交界面.
1.3 网格划分及无关性分析
文中根据伯努利能量方程计算对旋式轴流泵扬程H,由数值模拟计算得到的速度场和压力场以及叶轮上作用的扭矩来预测轴流泵叶轮的水力性能.
对旋式轴流泵扬程的计算公式为
H=(pTout-pTin)/(ρg),
(1)
式中:pTout为出口断面总压,Pa;pTin为进口断面总压,Pa;ρ为液体密度;g为重力加速度.
对旋式轴流泵效率的计算公式为
(2)
式中:M1和M2分别为电动机轴作用于前置叶轮和后置叶轮的力矩,N·m;ω为叶轮旋转角速度,rad/s;Q为流量,L/s;H为扬程,m.
由于计算精度受网格的质量影响较大,文中采用Turbo-Grid软件对前、后置叶轮进行网格划分,其余部件采用ICEM软件进行结构化网格划分,最终保证网格质量均在0.3以上.通过网格无关性验证满足数值模拟计算要求时,得到各部件网格数量,其中进水管道网格数量为24万,出水管道网格数量为35万,前置叶轮与后置叶轮网格数量均为58万.叶轮部件及出水管道网格图如图2所示.

图2 网格划分
对旋式轴流泵在运行时,前、后置叶轮起主导作用,因此前、后置叶轮的网格数量对数值模拟计算结果的精确性起决定性作用,故需对叶轮总网格数进行网格无关性分析,如图3所示.由图3可以看出,前、后置叶轮总网格数在110万时,网格数量的增加对泵装置效率的影响很小,为了减少计算工作量和节约计算资源,最终选取前、后置叶轮总网格数为116万左右.
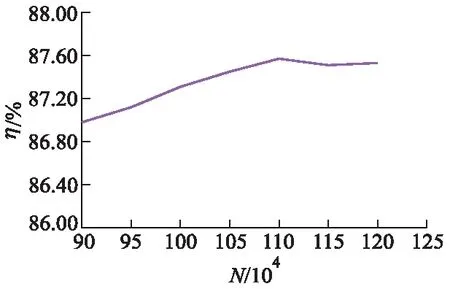
图3 对旋式轴流泵叶轮网格无关性分析
2 数值结果验证
模型泵采用ZML水泵水力模型.ZML模型泵由ZML叶轮和DYZML导叶组成.名义叶轮直径D1=300 mm,实际叶轮直径D2=299.65 mm. ZML叶轮实物如图4a所示,其轮毂比为 0.4,叶片数为4,叶轮采用黄铜材料经数控加工成形.DYZML导叶如图4b所示,其轮毂直径为110 mm,叶片数为7,采用钢质材料焊接成形.

图4 试验部件及系统实物图
图5为ZML水泵模型装置试验和数值模拟外特性对比情况.从图中可以看出,ZML水力模型数值模拟的Q-H和Q-η曲线均与对应试验曲线吻合得较好.设计工况Q=360 L/s时,ZML水力模型测试效率为84.48%,扬程为5.15 m.数值模拟最高效率为84.13%,试验测试最高运行效率为84.60%,偏差为0.47%.总体而言,数值模拟结果是准确可靠的.
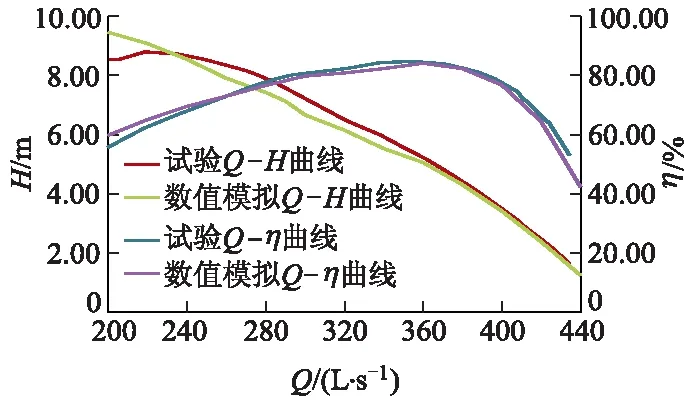
图5 ZML水泵模型装置试验与数值模拟外特性对比
将ZML水力模型叶轮数值模拟结果与对旋式轴流泵前置叶轮数值模拟结果进行对比,其外特性曲线如图6所示.ZML水力模型叶轮数值模拟结果与对旋式轴流泵装置前置叶轮数值模拟结果整体趋势一致,偏差较小.文中对旋式轴流泵的后置叶轮与前置叶轮为同一个叶轮.在性能上,前置叶轮水力性能与正常水泵叶轮性能一致,但后置叶轮与前置叶轮差别较大.文中针对后置叶轮的水力性能进行详细分析.
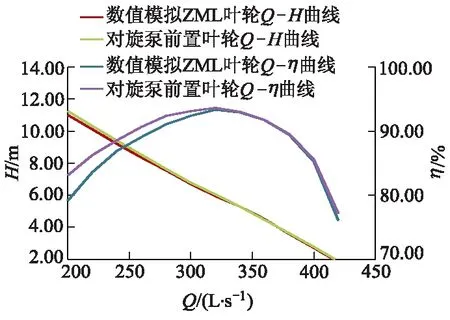
图6 ZML数值模拟与对旋泵前置叶轮外特性对比
3 计算结果分析
3.1 对旋式轴流泵外特性分析
对不同工况下对旋式轴流泵进行数值模拟,获取其不同工况下的水力性能,其性能曲线如图7所示.从图7可以看出,泵装置最优工况对应的流量为360 L/s,其最优效率为87.57%,扬程为11.32 m;而ZML水泵模型最优工况点流量为360 L/s,扬程为5.06 m,效率为84.13%.可见,在最优工况下,较ZML水泵模型对旋式轴流泵在最优工况点扬程提高了6.26 m,效率提高了3.44%.在小流量工况下,流量为300 L/s时,泵提前进入马鞍区,此时泵扬程为14.06 m,效率为79.48%;在大流量工况下,流量为440 L/s时,泵扬程为2.24 m,效率为54.16%.对旋式轴流泵装置高效区(最高效率点下降5.00%的2个点所对应的流量点之间的范围[14-15])范围更宽,扬程提高了约一倍.
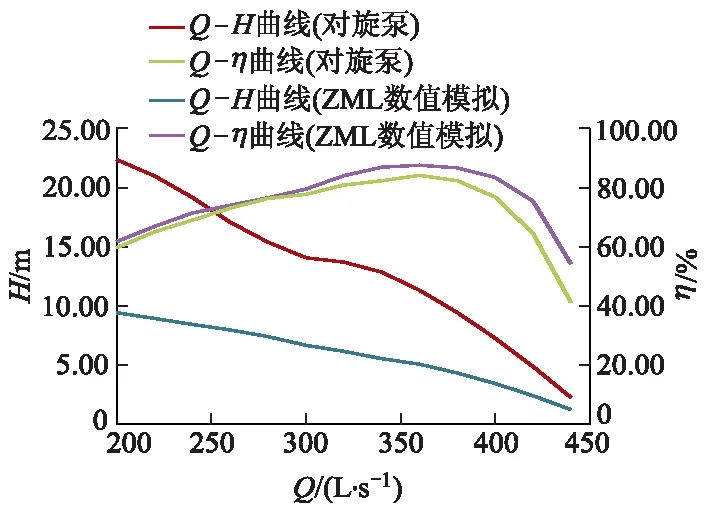
图7 对旋泵与ZML水泵模型外特性对比
从数值模拟结果发现,在扬程方面,各工况下对旋式轴流泵的扬程明显大于普通轴流泵;在效率方面,对旋式轴流泵效率曲线更加平坦、稳定,高效区范围更宽,且高效区往大流量偏移,高效区范围约为ZML水泵模型的1.5倍,最高效率为87.57%.
3.2 前、后置叶轮外特性对比分析
图8为对旋式轴流泵前、后置叶轮外特性曲线.从图8可以看出,在设计工况Q=360 L/s时,前、后置叶轮效率相差约1.02%,但后置叶轮扬程较前置叶轮扬程高3.01 m,进口流场的旋转会增加叶轮叶片的做功能力.后置叶轮Q-H曲线明显高于前置叶轮,以扬程开始出现正斜率时为临界点,后置叶轮提前进入马鞍区.
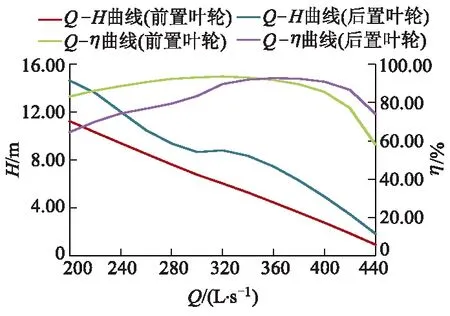
图8 对旋式轴流泵前、后置叶轮外特性对比
3.3 压力云图分布
图9,10分别为不同流量下前、后置叶轮的压力分布云图.由图可知,在各个流量工况下,后置叶轮吸力面与压力面的平均压差为711 795 Pa,大于前置叶轮的平均压差602 964 Pa,这也解释了对旋式轴流泵后置叶轮比前置叶轮扬程高的原因.在小流量工况下,对旋泵前、后置叶轮压力面的压力值沿轮毂到轮缘均逐渐升高,而吸力面的压力值沿叶片进口到出口逐渐升高.随着流量的增大,前、后置叶轮压力梯度变化较小,吸力面的压力值沿叶片进口到出口呈先减小后增大的趋势,且在叶片吸力面的中部存在明显的低压区,后置叶轮吸力面的压力梯度变化较大.在大流量工况下,对旋泵前、后置叶轮的压力面的进口处均存在明显低压区,这说明水流经过前置叶轮后其射流角度在后置叶轮背面.在设计流量工况下,对旋泵后置叶轮背面的压力梯度较前置叶轮变化较大,分布不均匀,使得后置叶轮效率明显低于前置叶轮效率.
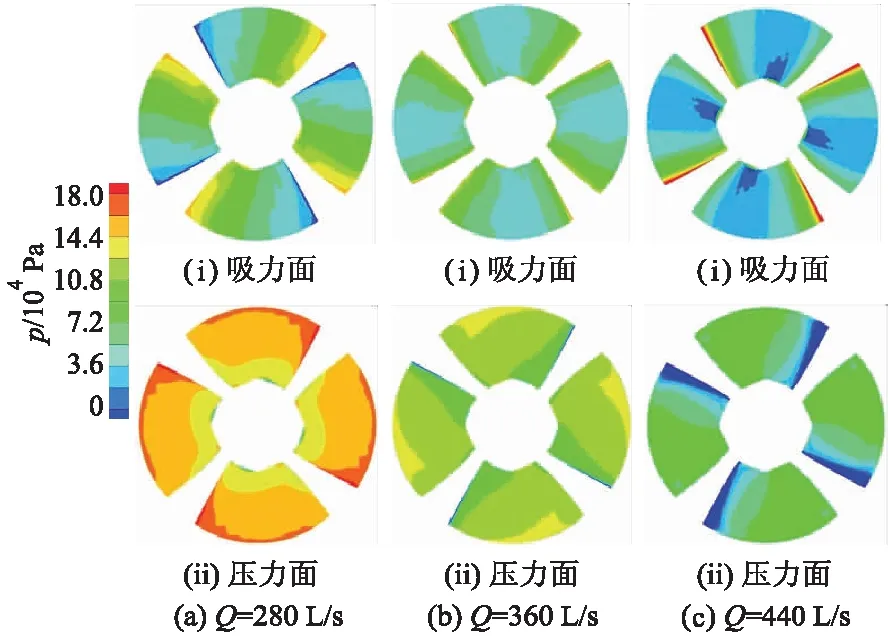
图9 对旋泵前置叶轮叶片压力云图
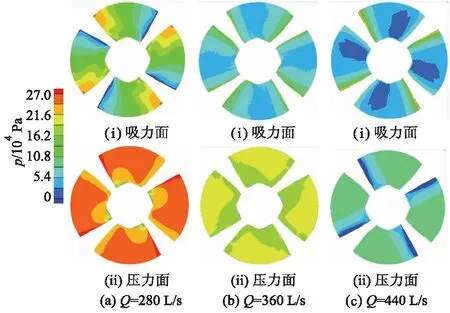
图10 对旋泵后置叶轮叶片压力云图
3.4 流场分析
对旋式轴流泵不同流量下前、后置叶轮的二维流线图如图11所示.由图11可以看出,在小流量工况下,后置叶轮内存在局部旋涡,且脱流现象严重,这会增加后置叶轮的水力损失,降低整个泵段的效率.随着流量增大,旋涡区域逐渐减小,在设计工况和大流量工况下,后置叶轮区域流态基本平顺,没有明显的脱流和旋涡区域.在小流量工况下,后置叶轮的进口液流角不合理,导致后置叶轮进口流场条件较差,从而干扰了后置叶轮出口处的流场分布.随着流量的增大,后置叶轮进口液流角分布逐渐合理,进水条件明显改善,后置叶轮内流态不断改善,无脱流和旋涡现象.
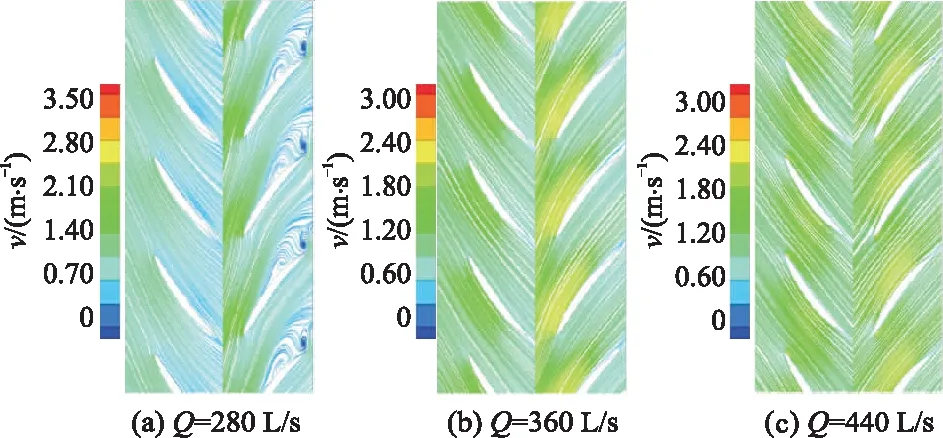
图11 对旋式轴流泵叶展方向0.2断面的二维流线分布
3.5 叶展方向进口液流角分布分析
设计工况下ZML叶轮断面翼型安放角与对旋泵前、后置叶轮从轮毂到轮缘方向的进口液流角α分布如图12所示.图中span表示叶轮叶展方向跨度,其中,轮毂处为0,轮缘处为1.0.从图中可看出,在设计工况下,前、后置叶轮进口液流角α变化趋势与ZML叶轮断面翼型安放角变化趋势一致,进口液流角从轮毂到轮缘呈现减小趋势.前置叶轮的进口液流角与ZML叶片进口角更为贴近,最大差别位于轮毂区域,相差约为12.69°,这在一定程度上说明了前置叶轮进口水流流态好,做功能力的稳定性好,流量-效率曲线高效区范围比较宽.后置叶轮进口液流角与ZML叶片安放角相差较大,在轮毂区域,ZML叶轮叶片安放角比后置叶轮进口液流角高了约20.64°;而在轮缘区域,后置叶轮和前置叶轮的进口水流均为负冲角,但后置叶轮进口液流角更接近叶片安放角,基本属于无冲击入流,这就导致了后置叶轮在大流量工况下效率要优于前置叶轮.总体上,后置叶轮的水流进口冲角要大于前置叶轮,导致后置叶轮叶片做功能力增强,后置叶轮扬程增大.
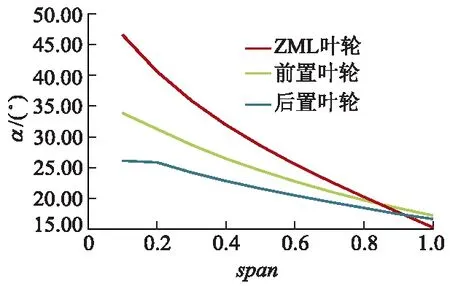
图12 对旋式轴流泵叶展方向进口液流角分布
3.6 后置叶轮安放角的影响分析
后置叶轮角度为0°时,水流经过前置叶轮进入后置叶轮的冲角较大,导致后置叶轮翼型工作能力下降.由于安放角越大,冲角越大,叶轮产生较大的脱流现象.为达到前置叶轮的水力性能,减小冲角,提高后置叶轮的水力性能,文中选择将后置叶轮安放角角度调整为-2°.外特性对比如图13所示,后置叶轮安放角为-2°时,其Q-H曲线略低于后置叶轮安放角为0°时,在设计工况Q=360 L/s时,两者扬程相差1.18 m.在小流量工况下,后置叶轮安放角为-2°时,其Q-η曲线略高于后置叶轮安放角为0°时,而在大流量工况下,后置叶轮安放角为-2°时,Q-η曲线略低于后置叶轮安放角为0°时,两者最大相差15.68%.这是由于后置叶轮安放角变小后,在轮缘处产生负冲角,压力面头部产生了较大的脱流现象,导致后置叶轮的做功能力降低,扬程曲线降低,效率曲线反而没有后置叶轮安放角为0°时稳定、高效.改变后置叶轮安放角,特别在小流量工况下,后置叶轮的马鞍区同样提前,后置叶轮的进口液流角几乎相同,未达到改变安放角理想效果.因此后置叶轮不能同前置叶轮设计相同,需要重新调整进口角度.
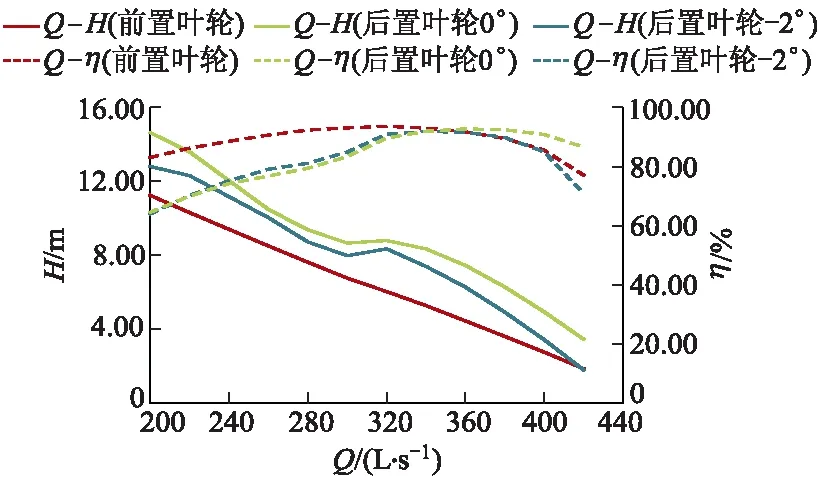
图13 对旋式轴流泵后置叶轮0°,-2°外特性对比
4 结 论
1) 对旋式装置最优工况对应的流量为360 L/s,其最优效率为87.57%,扬程为11.32 m;ZML水泵模型最优工况点流量为360 L/s,其扬程为5.06 m,效率为84.13%.故在最优工况下对旋式轴流泵扬程较ZML水泵模型提高了6.26 m,效率提高了3.44%.
2) 较普通轴流泵,对旋式轴流泵各工况下的扬程明显提高.效率曲线更加平坦、稳定,高效区范围更宽广,且高效区往大流量偏移,高效区范围约为普通轴流泵的1.5倍.
