基于改进人工蜂群算法的废旧产品拆卸规划
2023-02-21马淑梅陆星润徐立云
马淑梅 陆星润 徐立云
(同济大学 机械与能源工程学院,上海 201804)
拆解回收再利用废旧产品可以有效减少环境污染,助力实现“双碳”目标,对节能减排和资源再生具有重要意义。选择性拆解规划(Selective Disassembly Planning,SDP)问题作为拆解回收阶段的难点,极大地影响了拆解效率和收益,因而受到人们的广泛关注。
1 考虑碳排放的SDP模型
1.1 SDP问题描述
现阶段SDP问题的研究主要包括拆解度、拆卸序列以及拆卸单元的回收方式3个方面。传统SDP模型在跨度上仅仅考虑拆解回收阶段而忽略对其他阶段的影响,因此文章从产品生命周期的角度出发,分析不同回收方式对零部件原材料获取和制造阶段的影响,构建考虑碳排放的SDP模型。合理回收废旧产品的零部件,能够抵消或减少因重新生产零部件和加工原材料产生的碳排放。
1.2 碳排放拆卸混合图模型
图模型主要有无向图、有向图、与或图以及混合图模型。其中,有向图具有建模简单和易于求解的特点,但功能相对单一,无法完整表述产品的拆卸信息。因此,本文在有向图的基础上加入联接特征的碳排放信息,提出了碳排放拆卸混合图模型[1]。
碳排放拆卸混合图可以表示为G={VP,VC,DE},其中顶点VP={vp1,vp2,…,vpn}表示拆卸单元,n为拆卸单元总数,联接特征VC={vc1,vc2,…,vcs}表示拆卸单元之间的联接件和联接方式,s为拆卸特征总数,联接特征通过虚线连接两端的拆卸单元。优先约束表示图的边,两者之间存在强制性的拆卸优先关系,记为DE={de1,de2,…,dew},用实线箭头表示。有向边由优先级低的拆卸单元指向优先级高的拆卸单元。如图1所示,该碳排放拆卸混合图中包含8个拆卸单元和5个联接特征。

图1 碳排放拆卸混合图
1.3 模型优化目标
1.3.1 拆卸时间最小
拆卸时间主要包括拆卸单元从拆卸主体分离的时间ti、常规拆卸联接特征的时间tcm、破坏式拆卸联接特征的时间tdm和工具变换消耗的时间ttoolpq。因此,最小化拆卸时间f1min可以表示为

1.3.2 拆卸利润最大
拆卸利润由回收拆卸单元和联接特征的总收益Rvp、Rvc去拆卸成本f3、拆卸单元和联接件回收过程中的做工成本RCvp、RCvc得到,因此最大化拆卸利润f2max可以表示为
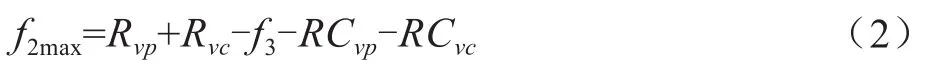
拆卸成本主要包括拆卸过程中消耗的人工成本Swf1、常规拆卸工具消耗成本Cr以及破坏式拆卸工具消耗成本Cr*,故拆卸成本f3min可以表示为

式中:Cr、Cr*可参考文献[1]进行估算。
1.3.3 减少的碳排放最多
产品拆解回收对不同阶段碳排放的影响主要包括拆解过程中因拆卸操作产生、回收过程中因回收再加工产生以及通过不同回收方式回收拆卸单元而抵消或减少的碳排放量。最大化减少的碳排放f4max表示为

拆解过程中产生的碳排放量Gd是拆卸联接特征产生碳排放的总和,即

因回收减少的碳排放量Gr为

拆卸单元vpi在不同的回收方式下减少的碳排放量Gik的计算为

拆卸单元再利用和再制造时,减少的碳排放Gi1和Gi2为抵消的原材料获取阶段的碳排放制造阶段的碳排放GEi减去因回收产生的碳排放GCiK;对拆卸单元进行材料回收时,减少的碳排放Gi3为抵消的原材料获取阶段的碳排放减去因回收产生的碳排放;进行废弃处理时,减少的碳排放Gi4为0。再利用、再制造和材料回收过程中产生的碳排放量Gi1、Gi2和Gi3可以从回收作业中获取。拆卸单元制造阶段产生的碳排放GEi以文献[2]提出的制造过程碳排放量化方法进行估算[2]。
2 改进人工蜂群算法
人工蜂群算法在多目标优化问题求解中表现出求解高效和结果理想等特点,因此提出改进的多目标人工蜂群算法(Improved Artificial Multi-objective Bee Colony Algorithm,IMOABC),可用于求解多目标SDP问题。
IMOABC算法的详细运算流程如下。
步骤1:设定蜜源个数PS、最大迭代次数、蜜源开采次数上限limit以及外部档案容量Q。
步骤2:初始化蜜源,通过非支配排序和拥挤度计算初始化外部档案Q。
步骤3:通过交叉操作在雇佣蜂的领域内产生新的蜜源。
步骤4:判断新蜜源是否被原蜜源支配,若被支配则将原蜜源分配给雇佣蜂,否则将新蜜源分配给雇佣蜂,并将开采度设为0。
步骤5:重复步骤3和步骤4,更新PS个雇佣蜂的蜜源。
步骤6:按锦标赛规则从雇佣蜂中选取2个较好的个体进行交叉操作产生新的蜜源。
步骤7:判断新蜜源是否被原蜜源支配,若被支配则继续开采原蜜源分配,并将其开采度加1,否则将新蜜源分配给观察蜂,将开采度设为0。
步骤8:重复步骤7和步骤8,更新PS个观察蜂的蜜源。
步骤9:检查各蜜源的开采次数是否大于开采上限,若大于则转化为侦查蜂寻找新的蜜源,并将开采度设为0。
步骤10:检查是否有重复的蜜源,若有,对重复的蜜源进行重构。
步骤11:进行非支配排序和拥挤度计算,更新外部档案Q。
步骤12:重复步骤4至步骤12,直到迭代次数达到最大迭代数,得到问题的Preto解集。
采用三链表结构对蜜源进行编码,记为v={v1,v2,v3}。v1={a1,ai,…,an}表示拆卸序列,ai为第i个被拆卸的拆卸单元。v2={b1,b2,…,bn}表示v1中对应拆卸单元的拆卸方式,其值代表拆卸方式编号。v3={c1,c2,…,cn}标记v1中对应拆卸单元的回收方式,其值代表回收方式编号。根据文献[2]中可行解的方法随机生成PS个完全拆卸序列,定义变量hlast表示完全拆解序列v1中最靠后的目标拆卸单元的编号,保证实际拆解序列长度L不小于hlast,即可生成符合约束要求的不完全拆解序列,其计算公式为

依据上述操作得到可行的拆解方案,将生成的蜜源记为v´={v1,v2,v3,L}。
为确保雇佣蜂阶段交叉后生成的新v1仍能满足优先约束关系,采用优先保存交叉(Precedence Preservative Crossover,PPX)的方法对2个个体方案进行交叉操作。PPX交叉操作流程:随机生产一条由2个父代个体编号组成的序列,长度与个体长度相等;根据随机生成的序列,依次从各自父代个体上选取子代基因将其插入子代个体,并在父代个体上删除该基因。重复该过程,直到所有子代基因选择完毕[3]。
图2描述了一个简单的PPX交叉过程。执行PPX的父代个体均为完全拆卸序列。为拆除所有目标拆卸单元,每个交叉后的子代个体需要根据式(8)随机生成对应的L。

图2 PPX过程
在观察蜂阶段采取锦标赛选择策略,选取2个局部最优个体进行PPX交叉操作,结合贪心策略将比较后较优的蜜源分配给观察蜂进行采蜜工作,以提高蜂群的寻优能力[4]。第一,确定选取的个体数量N。第二,从种群中随机选择N个个体。个体被选择的概率相同,根据个体的非支配等级和拥挤距离进行排序,选择最优者作为PPX交叉操作的父代之一。第三,重复第二步的操作选取另一个父代,执行PPX交叉操作生成新个体。将产生的新个体与原种群个体比较,取代种群中表现较差的个体。第四,重复第二步和第三步的操作,直到所有观察蜂均被分配完毕。
3 实例应用
结合SDP模型和IMOABC算法,以某废旧变速箱为案例进行拆解规划。
3.1 案例数据收集
某双离合变速箱对应的拆卸混合图如图3所示。该变速箱主要由23个拆卸单元构成。变速箱内部单元的拆卸信息如表1所示。从拆卸单元的回收收益和危害性角度考虑,将编号为4、8、18和20的拆卸单元作为选择性拆卸的目标。

图3 碳排放拆卸混合图
其他无法直接收集和获取的SDP模型输入数据采用以下方式进行估算。查询相关设计手册中对应联接特征的参数,文献[5]中螺栓联接装配碳排放的计算方法,对拆卸螺栓联接产生的碳排放量进行GEol-m估算[5]。根据变速箱的BOM表,参考表1估算拆卸单元和联接特征原材料获取阶段产生的碳排放GMi。
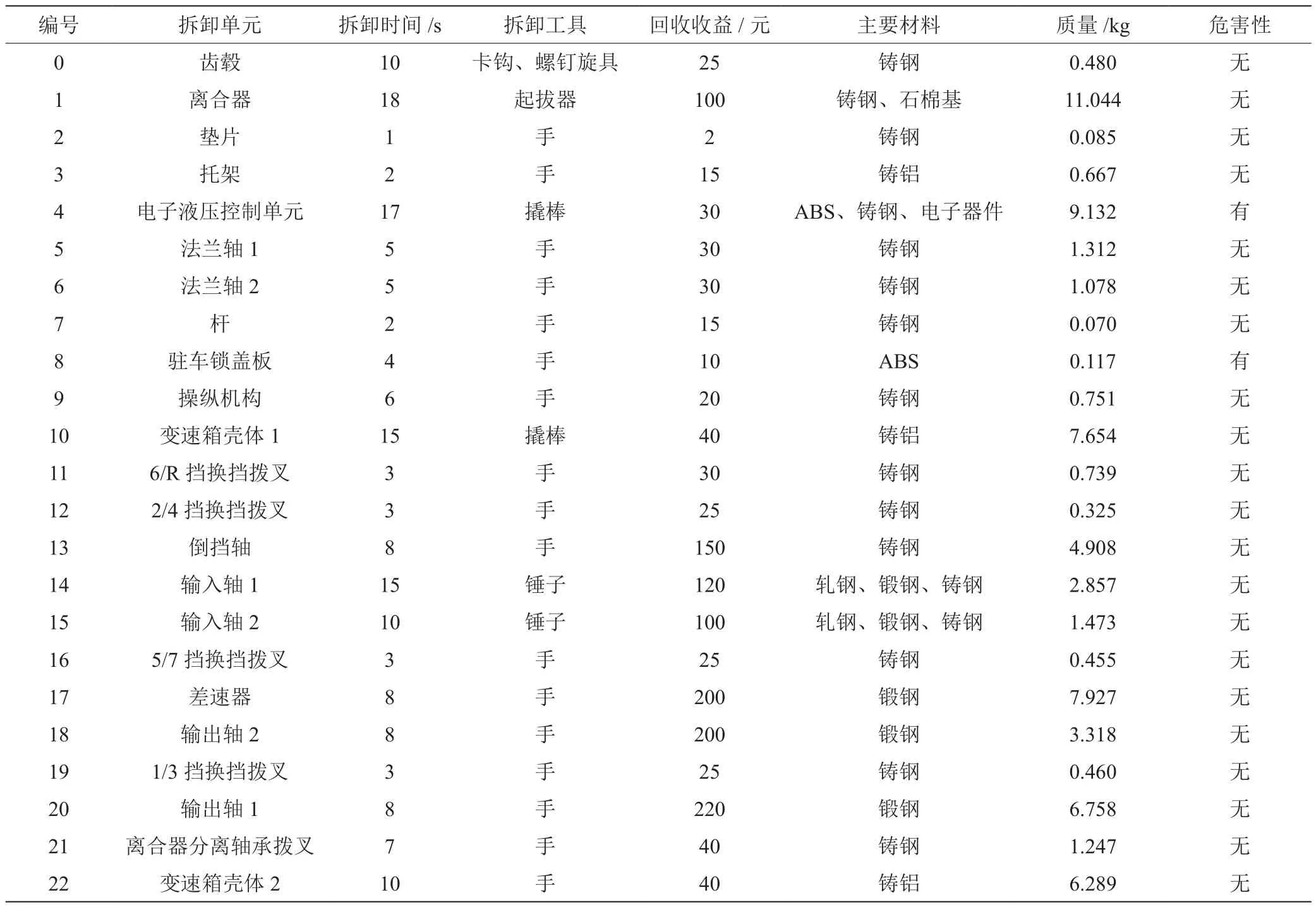
表1 变速箱内部单元的拆卸信息
3.2 试验结果分析
为验证IMOABC算法的全局性,与未改进的多目标MOABC、多目标快速非支配排序遗传算法(Non-dominant Sorting Genetic Algorithm-Ⅱ,NSGA-Ⅱ)以及人工鱼群算法(Artificial Fish-Swarm Algorithm,AFSA)进行比较。所有算法种群规模均设为100,迭代100次。各算法的参数设定如下:国际数学奥林匹克竞赛(International Mathematical Olympiad ABC,IMOABC)的选择个体数为35,蜜源开采上限为5;NSGA-Ⅱ的交叉概率为0.9,变异率为0.1;AFSA中觅食行为最大尝试次数为5,视野visual=50,拥挤度设为0.8。涉及的所有算法均在C++中编程,运行环境配置为Intel(R) Core(TM)i5-7 300HQ CPU处 理 器,NVIDIA GeForce GTX 1 050 2 GB显卡,2.50 GHz主频,12.0 GB内存。4种算法迭代后的Pareto前沿如图4所示,结果观察到IMOABC的Pareto前沿在分布、收敛和数量上都比其他算法更理想。IMOABC的Pareto解集如表2所示,可见拆卸利润越高的拆卸方案减少的碳排放越多,但要花费的拆卸时间越久。合适的拆卸方案可以根据决策者的期望选择,通常可以人为对优化目标设置权重进行排序选择。
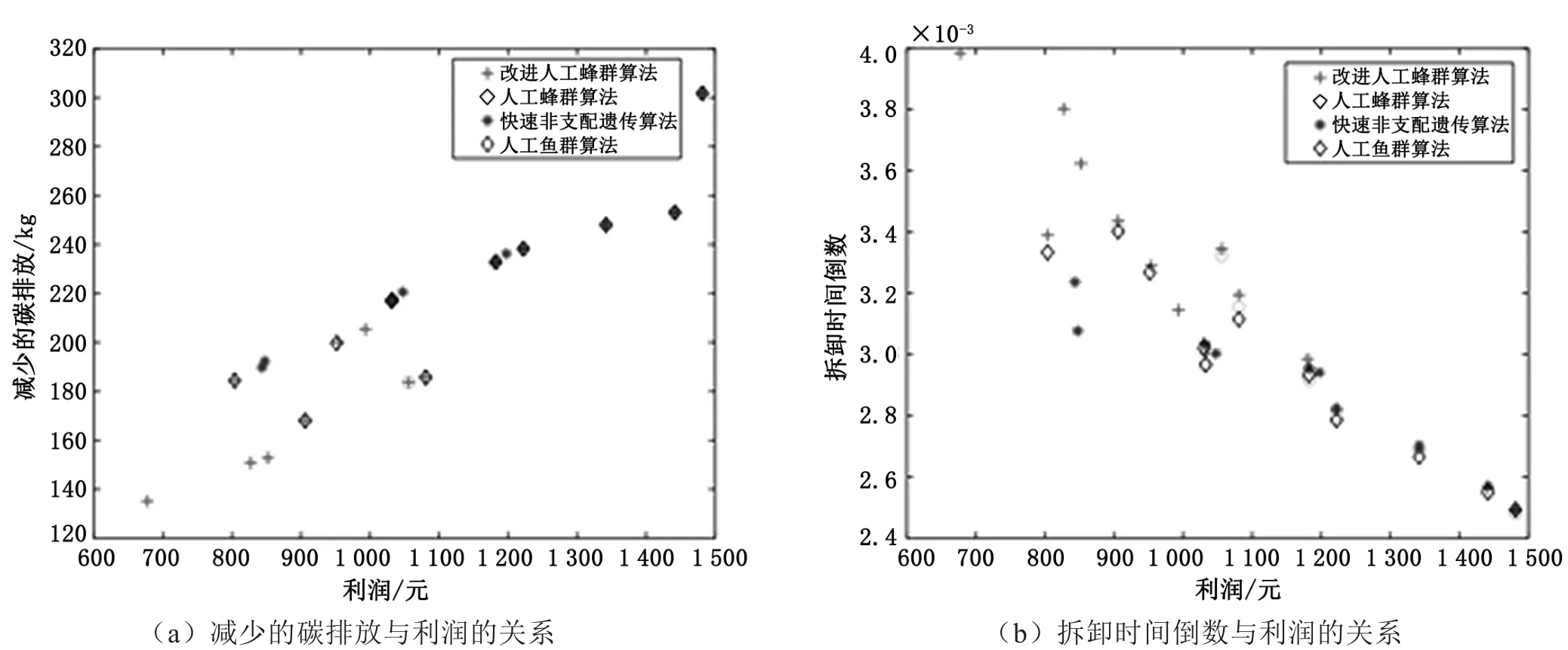

图4 不同算法的Pareto前沿
4 结语
针对废旧产品的拆解回收再利用,建立考虑碳排放的SDP模型,将拆卸利润、拆卸时间和减少的碳排放作为优化目标,采用IMOABC算法对该模型进行求解,获得高质量的Pareto解集,最后结合某双离合变速箱的拆解案例,验证模型和算法的可行性和高效性。
