基于BA-RVM算法的发动机故障诊断技术研究*
2023-02-20陈财森胡海荣程志炜房璐璐
陈财森,胡海荣,程志炜,房璐璐
(1.陆军装甲兵学院演训中心,北京 100072; 2.陆军装甲兵学院信息通信系,北京 100072;3.32167部队,西藏 拉萨 850000)
1 引言
为了打赢信息化战争,装备保障技术同样也需要信息化。发动机是装甲装备的核心部件,直接关乎到装甲装备的作战能力。传统的故障诊断技术已经不适用于大规模装甲装备的故障诊断,在信息化条件下,结合人工智能技术对故障进行预测判断,高效率高准确率地定位故障可以提高装备保障的质量,才能快速恢复战斗力。
1985年,美国的通用汽车公司就已经开始对汽车的发动机故障诊断进行研究[1],此后,一些发达国家的汽车发动机故障诊断系统也得到迅速发展。我国的发动机故障诊断技术研究起步较晚,但到目前为止,我国的发动机故障诊断技术也已经相对成熟。文献[2,3]利用神经网络对发动机的故障进行预测,并能确定故障的原因。文献[4]利用波形和数据流诊断汽车发动机的电控系统故障。故障诊断技术发展到现在,虽然结合了新的分析方法,如BP(Back Propagation)神经网络、支持向量机SVM(Support Vector Machine)和贝叶斯分布等算法,但是预测的准确率仍然不高,且由于应用对象不同,其技术还无法直接应用在装甲装备发动机的故障诊断上。
2 发动机故障参数分析
发动机运行时,传感器会采集发动机的各种参数,这些参数被称为数据流,包括发动机的节气门开度、转速、氧传感器等参数。本文采集如表1所示的9个典型的发动机参数进行分析。
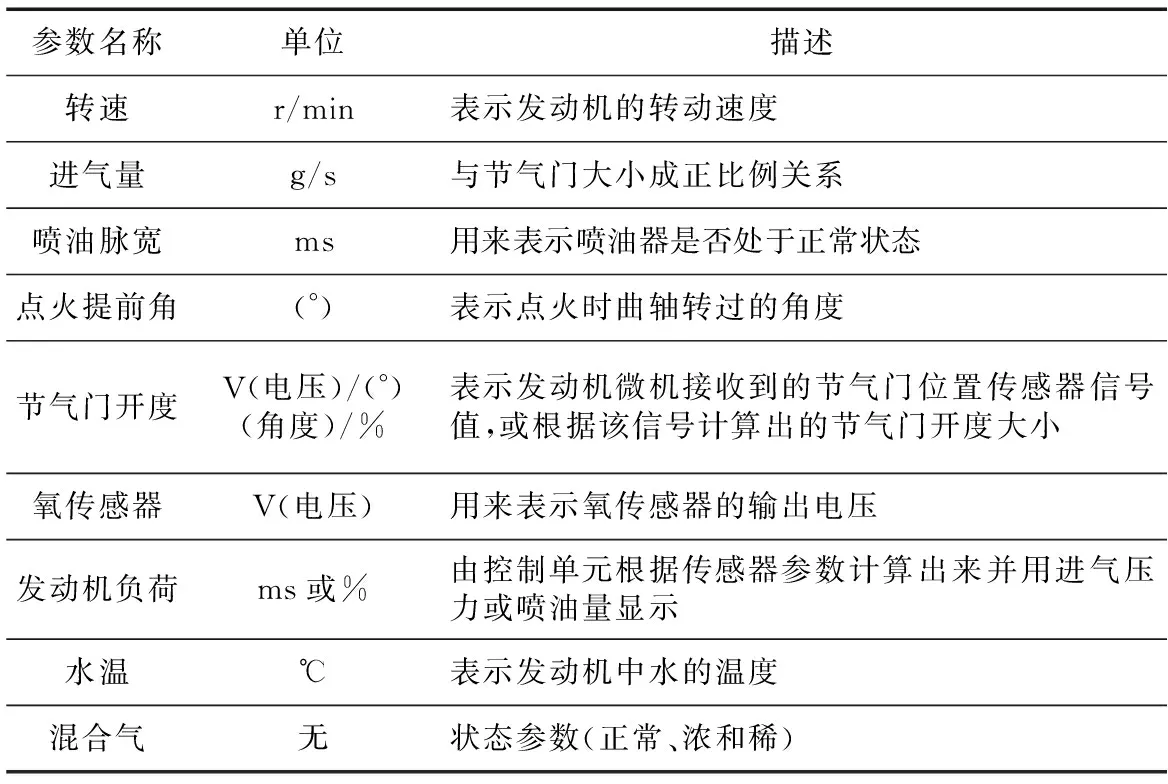
Table 1 Typical engine parameters表1 发动机典型参数
通过分析表1所示的9个参数,能够确定6种故障,分别是空气流量计故障、氧传感器故障、水温传感器故障、节气门故障、喷油器故障和空气滤清器故障。不同的传感器采集数据的单位不一致,导致这些数据无法直接使用。因此,在使用数据前,必须对其进行预处理,以免某一个参数的巨大变化导致模型预测失真。通过采集大量的发动机参数信息与故障信息,训练出一个合理的预测模型,然后直接输入传感器参数的数据快速准确地得到故障类型。
3 基于BA-RVM算法的发动机故障诊断模型
3.1 蝙蝠算法
剑桥大学Yang教授[5]在2010年提出一种模拟蝙蝠捕获猎物时使用超声波的启发式搜索算法,被称为蝙蝠算法BA(Bat Algorithm)。蝙蝠在利用超声波判断猎物的过程中,如果靠近猎物,其发出的脉冲数量将会增加,并且响度会减小,直到蝙蝠捕获猎物。蝙蝠寻找猎物的过程可转换为寻找最优解的问题。蝙蝠算法将每一个蝙蝠作为搜索空间的一个解,通过蝙蝠随机飞行产生的适应值来寻找下一次迭代的最优值,当蝙蝠随机飞行产生的适应值优于飞行之前的适应值,则更改蝙蝠的位置,否则保持蝙蝠的位置不变,将在下一次迭代中继续随机飞行,直到得到比当前蝙蝠的适应值更优的位置。所以,蝙蝠总是朝着最优解前进,最终收敛于问题的最优解。与遗传算法和粒子群优化算法相比,蝙蝠算法的效率和准确率都有明显的提高[6]。在算法循环迭代过程中,通过改变蝙蝠的速度、响度和频率来寻找局部最优解,直到局部最优解收敛或者完成指定迭代次数。
算法1蝙蝠算法BA
输入:所有蝙蝠的位置xi,所有蝙蝠的速度vi。
输出:最优蝙蝠的位置xbest。
步骤1初始化蝙蝠位置xi和蝙蝠的初始速度vi,其中i∈[1,n],n为种群的数量。
步骤2初始化种群飞行时脉冲响度Ai、脉冲发射率ri及脉冲频率fi,并确定频率搜索范围[fmin,fmax],根据适应值函数计算初始化蝙蝠种群的适应值,并记录最优适应值fitnessbest和最优位置xbest。

fi=fmin+(fmax-fmin)β
(1)
(2)
(3)
其中,β∈[0,1]是服从均匀分布的随机数,xbest为全局最优位置。
步骤4生成一个随机数rand1,如果rand1大于脉冲发射率ri,对最优蝙蝠位置xbest进行扰动,产生新值进行替换,以降低算法陷入局部最优的概率。扰动公式如式(4)所示:
(4)
其中,ε是[0,1]的随机数,A(t)是当前时刻t时所有蝙蝠脉冲响度的平均值。
步骤5再次生成一个随机数rand2,如果rand2小于脉冲响度Ai且更新后的位置适应值fitnessi (5) (6) 其中,α∈(0,1),γ>0。 步骤6重复执行步骤3~步骤5,直至满足设定的最优解xi的条件或者达到最大迭代次数。 步骤7输出全局最优适应值和最优解。 ti=y(x;ω)= (7) 其中,ωi表示权重,δ是服从N(0,σ)分布的噪声,x表示位置矩阵,ω表示权重向量,K(x,xi)是核函数,Φ(x)由N×(N+1)阶的核函数构成,如式(8)所示: (8) 本文假设ti服从独立分布,样本的概率表达式如式(9)所示: p(t|ω,σ2)= (9) 其中,t表示ti的矩阵。为防止ω和σ2过渡拟合,一般使用高斯先验概率分布对参数进行约束,如式(10)所示: (10) 其中α为N+1维超参数向量。 后验分布基于Bayes公式,如式(11)和式(12)所示: p(ω|t,α,σ2)=(2π)-(N+1)/2|Σ|-1/2× (11) μ=σ-2ΣΦ(x)2t Σ=(σ-2Φ(x)TΦ(x)+A)-1 (12) A=diag(α0,α2,…,αN) 这里统一使用超参数表示,RVM的概率表达式p(t|α,σ2)的定义如式(13)所示: (2π)-(N+1)/2|σ2Ι+Φ(x)A-1Φ(x)T|-1/2× (13) 最后求解p(t|α,σ2)的最大值,如式(14)所示: p(t|α,σ2)∝p(t|α,σ2)p(α)p(σ2) (14) 从而得到求解最大值的公式,如式(15)所示: (15) 设新的输入和输出为(x*,t*),通过以上分析,输出t*的均值和方差如式(16)和式(17)所示: y*=μTΦ(x*) (16) (17) 核函数能够将复杂难分的数据映射到高维空间,使数据更容易区分,RVM常用的核函数有: (1)高斯核函数:对样本数据的维度和大小没有限制,局部寻优能力较强,应用较为广泛,如式(18)所示: (18) 其中,p和q是空间中任意2点的向量表示。 (2)多项式核函数:与高斯核函数相比,多项式核函数的全局寻优能力更强,但是参数n调节过大时,容易产生过拟合现象,且需要消耗大量的计算资源,如式(19)所示: K(p,q)=(apTq+c)d (19) 其中,a表示调节参数,c用来设置核函数中的coef,d表示最高次项次数。 (3)拉普拉斯核函数:是高斯核函数的一个变种,具有降低核参数敏感性的特征,如式(20)所示: (20) 在RVM训练的过程中,通过迭代得到最终的模型权重值,再根据式(7)进行分类。文献[7]在求RVM参数时,通常把核矩阵剪枝阈值设置为107,终止迭代阈值设置为10-3,以便在有限迭代中尽早获取合适的参数。 RVM算法的核心是获取一个合适的参数,因此核函数的选择对RVM算法分类结果的影响特别大,将直接影响RVM的判断准确率。本文使用BA作为核函数来寻找RVM的最优参数。 算法2BA-RVM算法 输入:BA和RVM算法参数。 输出:xbest。 步骤1初始化BA和RVM算法的参数,并按照Tipping[7]的经验值设置核矩阵剪枝阈值。 步骤2确定RVM的目标函数,把BA中的蝙蝠作为当前RVM核参数宽度计算目标的值,得到最优位置xbest。 步骤3对蝙蝠的速度vi和位置xi进行随机更新。 步骤4计算蝙蝠的目标函数值,如果优于目标函数值xbest,则更新局部最优位置xbest。 步骤5重复步骤3和步骤4,直到迭代次数达到最大或满足RVM的阈值条件。 基于BA算法自适应核参数RVM的流程如图1所示。 Figure 1 Flow chart of adaptive kernel parameter RVM based on BA 图1 基于BA自适应核参数RVM的流程图 发动机传感器采集的每个参数的量纲和单位不一样,如果不对数据进行预处理,将会导致数值大的参数对结果影响过大,所以在数据分析前,需要对样本数据进行归一化处理,以保证实例各参数值处于同一个数量级,消除不同量纲之间的差异。通常归一化有线性归一化(Min-Max Scaling)和Z-score标准化(Z-score Standardization)2种方法: (1)线性归一化,如式(21)所示: (21) 其中,Xi表示样本实例数据,Xmin表示样本实例数据的最小值,Xmax表示样本实例数据的最大值,X*表示归一化处理后的数据。这种归一化也叫做离差标准化,通过对样本实例数据进行线性变化,使处理后的数据值在[0,1]。这种方法适合样本实例数据比较稳定,没有异常极端值的情况。 (2)Z-score标准化,如式(22)所示: (22) 其中,Xi表示样本实例数据,μ表示样本实例数据的均值,σ表示样本数据的标准差,X*表示归一化处理后的数据。经过Z-score标准化后的数据符合高斯分布,这种方法适合处理样本实例数据存在异常值和较多噪声的情况。通过Z-score标准化,能够避免异常值和极端值给结果带来的影响。 本文实验的操作系统环境为Ubuntu 18.04,CPU为Intel Core i5-7500,显卡为NVIDIA GTX1050i,内存为16 GB。在发动机故障诊断中,选择高斯核函数和线性归一化函数的预测效果最佳[8]。本文的6种故障类型属于离散数据,为了让分类器更好地处理数据,实验对故障类型和正常状态进行one-hot编码,编码规则如表2所示。 Table 2 One-hot coding of fault type 表2 故障类型one-hot编码 本文采集12/200ZL型水冷废气涡轮增压柴油机的样本数据500条,其中400条用于训练,100条用于测试(随机从总样本中抽取)。通过使用线性归一化函数,将数据进行归一化处理,部分样本数据如表3所示。 Table 3 Normalized engine data stream表3 归一化后的发动机数据流 为了让实验结果更具代表性,本文同时使用BP神经网络和SVM算法对同一份数据进行训练预测并将测试结果与BA-RVM的进行比较。首先使用BP神经网络对数据进行训练预测,将BP神经网络的隐藏节点设置为10,测试结果如图2所示。图2中的纵坐标表示故障编码,横坐标表示测试样本的编号。从图2可以看出,BP预测的错误率为12%,结果较为理想。 Figure 2 Testing results of BP neural network图2 BP神经网络的测试结果 BA-RVM算法的测试结果如图3所示。可以看到,错误率只有3%,与BP算法相比,错误率降低了66.67%;与SVM算法相比,错误率降低了62.5%。由于RVM中有大量的矩阵运算,在训练过程中,消耗的时间较长,约为SVM算法的6倍,但是在预测判断时,所消耗的时间少于SVM的,能够快速准确地给出结果。综合分析可知,基于BA-RVM算法的发动机故障预测要优于基于BP算法和SVM算法的,并能够快速定位故障类型。 Figure 3 Testing results of BA-RVM algorithm图3 BA-RVM算法的测试结果 本文针对传统检测技术在大量故障装备中难以准确快速诊断发动机故障,且诊断工作量大、效率低等问题,提出一种基于BA-RVM算法的发动机故障诊断模型。通过分析蝙蝠算法BA获得最优解的特点和相关向量机算法原理,结合装甲装备发动机的状态参数特点,在故障诊断分析模型训练时,采用蝙蝠算法对相关向量机算法RVM的核参数宽度进行调节优化,使用BA作为核函数来寻找RVM的最优参数,从而得到RVM最优参数的预测模型。实验结果表明,本文所提的基于BA-RVM算法的模型与基于BP算法的模型相比,错误率降低了66.67%;与基于SVM算法的模型相比,错误率降低了62.5%。基于BA-RVM算法的发动机故障诊断模型不仅能够快速地给出预测结果,而且预测准确率还较高。3.2 相关向量机算法
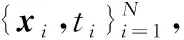
3.3 BA-RVM算法

3.4 数据特征归一化方法
4 实验与结果分析




5 结束语
