基于改进PSO-DE融合算法的风电场储能容量优化配置
2023-02-20陈涛邢金晶刘闯卢银均李俊陈海旭
陈涛,邢金晶,刘闯,卢银均,李俊,陈海旭
(1.国网湖北省电力有限公司荆门供电公司,湖北 荆门 448000;2.三峡大学电气与新能源学院,湖北 宜昌 443002;3.国网福建省电力有限公司福州供电公司,福建 福州 350000)
0 引言
随着国家“双碳”目标的提出,可再生能源将在未来能源市场中扮演越来越重要的角色。风是一种可再生能源,清洁无污染,且分布广泛,推广和使用风力发电能够有效减少碳排放量,缓解能源危机[1-2]。我国幅员辽阔,海岸线狭长,陆海风能资源都十分丰富[3],但风电功率随机性和波动性较大,在并网过程中会对电力系统稳定性和安全性造成威胁[4-5]。研究表明,在风电场配置一定储能设备能够有效抑制风功率波动,提高风电利用率[6-8],因此对风电场储能容量优化配置进行研究,具有十分重要的战略意义。
在风电场储能优化配置方面,刘颖明等人建立了风电集群储能容量优化配置模型,并采用蚁狮算法求解得到了储能系统容量及功率配置方案[9]。杨晓雷等人建立了包含储能系统总投资成本、电压偏差和有功损耗的多目标优化配置模型,并利用立方混沌映射策略对鲸鱼算法进行改进,采用改进鲸鱼算法对多目标模型进行了求解,算法分析验证了改进鲸鱼算法在风电场储能系统选址定容的有效性[10]。韩邵丹建立储能优化配置模型时考虑了机组运行成本、风险成本和储能成本,并给出了相应约束,建立了基于人工蜂群算法的储能优化配置机会约束目标规划模型[11]。此外,遗传算法、粒子群算法也被应用到风电场储能优化配置领域[12-13]。目前风电场储能优化配置模型虽然很多,但优化目标过于单一,大多为经济效益和储能投资成本,模型的求解精度也有待进一步提高。
基于此,以蓄电池作为风电场储能设备,综合考虑蓄电池投资成本和风电场弃风率,建立风电场储能容量优化配置模型,利用改进粒子群差分融合算法对风电场的最优储能容量进行计算,并结合算例分析对风电场最优储能容量配置的合理性进行论证。
1 风电场储能优化配置模型
1.1 蓄电池数学模型
蓄电池安装方便、功率响应迅速,能够有效平抑风电场功率波动。假设风电场以蓄电池作为储能设备,令t时刻风电场功率波动为ΔP(t),则
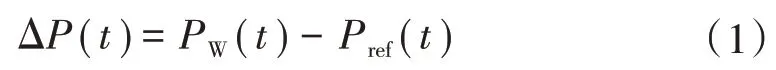
式中:PW(t)为风电场在t时刻的输出功率;Pref(t)为调度时间窗口内PW(t)的平均值,又称为输出功率参考值,调度时间窗口由调度部门根据负荷需求确定。
在充放电过程中,蓄电池的充放电功率均有限制,其充放电功率为

式中:Pbatcmax和Pbatdmax分别为蓄电池的最大充电功率和最大放电功率。
如果蓄电池的充放电功率Pbat(t)>0,则处于充电状态,反之,如果Pbat(t)>0,则处于放电状态。
蓄电池充放电过程中需要考虑容量及最大充放电功率的影响,因此其充放电模型分为充电和放电两种不同的情况[14]。
1)蓄电池充电。如果ΔP(t)>0 且蓄电池的蓄电量未达到其最大容量Cbat.N,在此过程中,蓄电池会一直充电,充电过程中容量和功率的表达式分别为
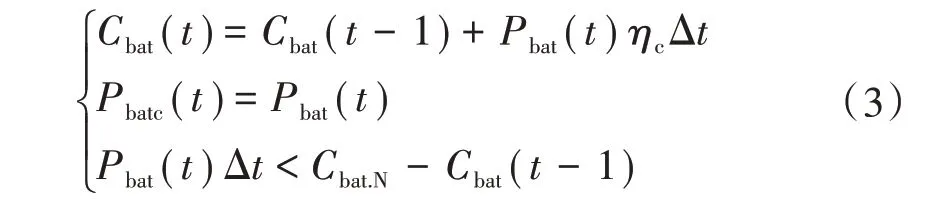
式中:Cbat(t-1)、Cbat(t)分别为蓄电池在t-1时刻和t时刻的容量;Δt为风电功率采样时间间隔;ηc为充电效率,取值范围为[0.65,0.85];Pbatc(t)为t时刻蓄电池的充电功率,Pbatc(t)>0。
当t时刻蓄电池充电至最大容量,即停止充电,未利用的风电功率通过卸荷器进行卸载,则有

2)蓄电池放电。如果ΔP(t)<0 时且蓄电池的电量未释放至最小容量Cbat.min,在此过程中,蓄电池一直放电,则放电过程中容量和功率的表达式为
式中:ηd为放电效率,ηd=1;Pbatd(t)为t时刻蓄电池的放电功率,Pbatd(t)<0。
当t时刻蓄电池放电至最小容量,即停止放电,则有

1.2 目标函数
风电场配置不同容量的储能设备,其投资成本和风电功率平抑效果会产生较大差异,储能蓄电池容量越大,投资成本越大,但风电功率平抑效果越好,风电场弃风率越小,反之,投资成本越小,风电场弃风率越大。因此为了获得更大的经济效益,应使二者平衡。综合考虑考虑蓄电池投资成本和风电场弃风率,分别建立相应的目标函数。
蓄电池投资成本的目标函数为

式中:ρ为蓄电池单位容量所需的成本,万元/MWh。风电场弃风率的目标函数为

式中:T为调度周期;SL(t)为t时刻风电场有无弃风现象的布尔量。
如果t时刻ΔP(t)>0 时且蓄电池的蓄电量已充电至最大容量,则蓄电池在t+1时刻结束充电,t+1时刻后损失的电能即为弃风能量电量,SL(t)的取值为
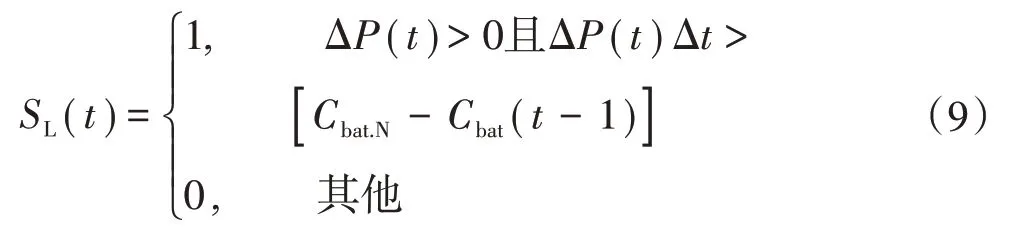
由此可见,风电场储能容量配置模型的有两个目标函数。为了简化计算,利用补偿系数将多目标函数转化为单目标,该目标函数称为综合成本,其表达式为

式中:λ为补偿系数,其作用是让蓄电池投资成本f1和风电场弃风率f2具有相同数量级。参考文献[15],λ取8×105元。
1.3 约束条件
1)蓄电池容量约束条件为

式中:Dd为蓄电池的放电深度。
2)充放电功率约束条件为
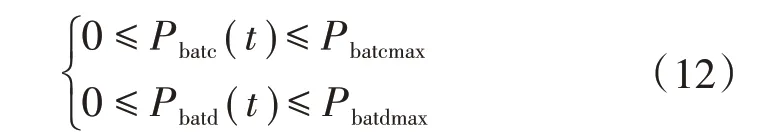
3)风电功率波动约束条件为
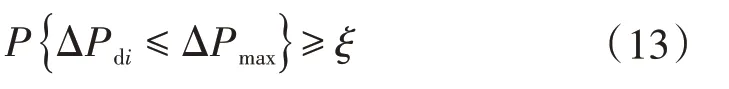
式中:ΔPdi为风电场安装第i个储能蓄电池后的功率波动值;ΔPmax为ΔPdi的最大值;ξ为风功率波动约束的可信度水平。
4)蓄电池荷电状态约束为
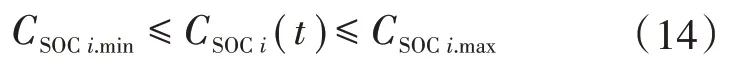
式中:CSOCi(t)为t时刻蓄电池的荷电状态;CSOCi.min和CSOCi.max分别为第i个储能设备的荷电状态的最小值和最大值。
1.4 平抑风功率波动评价指标
风电场安装配置储能设备后,风电功率波动幅度相对于安装前将有所下降,为了对储能设备的风功率波动平抑效果进行评价,通过计算有功功率偏差率α对此进行评价,其计算公式为

式中:Pd(t)为t时刻风电场安装配置蓄电池后的风电功率。
2 模型求解
2.1 改进PSO-DE融合算法
PSO-DE 融合算法是结合粒子群算法和差分进化算法寻优特点提出的一种优化算法[16-17]。PSO 算法和DE 算法虽然都能完成寻优,但两种算法的个体生成过程不同,PSO-DE 融合算法能够使两个种群中的信息更好地交流,在迭代过程中始终选择两个种群的整体极值进入下一代,避免单一算法在寻优过程中陷入局部最优。PSO 算法[18]和DE 算法[19]的群体极值可表示为


式中:θ(·)为适应度函数值。
PSO-DE 融合算法虽然融合了PSO 算法和DE 算法的寻优特点,解决了算法陷入局部最优的问题,为了进一步提高算法的计算精度,从三个方面对PSO-DE 融合算法进行改进。
1)惯性权系数调整。在PSO-DE融合算法中,惯性权系数被设置为固定值,为了增强算法前期的全局搜索能力和后期的局部寻优能力,对惯性权系数进行如下调整,具体公式为

式中:β(k)为第k次迭代时的惯性权系数;βstart、βend分别为惯性权系数的初值和终值;δ为控制因子。
2)越界粒子变异操作。PSO-DE 融合算法在寻优过程会出现粒子越界的现象,常规方法是使越界粒子的速度等于边界值,这样会降低粒子的多样性,降低算法的全局搜索能力。为此,对越界粒子执行变异操作,具体为
式中:uk为PSO 算法中粒子第k次迭代时的个体极值;umax、umin分别为粒子运动范围的上、下限;γ为变异率;r为[0,1]之间的随机数。
3)粒子初始化规则调整。为了使PSO-DE 融合算法中不同种群间更好地信息交流,PSO 算法和DE算法中的元素应当属于同一区间[zmin,zmax],为了保持种群多样性,将粒子初始化规则进行调整,具体为:

式中:hk为DE算法中粒子第k次迭代时的个体极值。
2.2 改进PSO-DE 融合算法求解风电场储能优化配置模型
采用改进PSO-DE 融合算法对风电场储能容量配置模型进行求解,具体步骤为:
步骤1)设置调度周期和调度时间窗口,并向有关部门获取风电功率PW(t)及风电功率参考值Pref(t)。
步骤2)设置PSO-DE 融合算法相关参数:种群规模为30,最大迭代次数为300,阈值为0.1,惯性权系数初值和终值分别为0.9 和0.4,加速因子为2.05,DE 加权系数、变异算子和变异率分别为0.5、0.8和0.01。
步骤3)根据综合成本的目标函数计算蓄电池最大容量Cbat.N个体适应度值。
步骤4)参数初始化,将种群中的个体分配给种群PPSO和PDE,利用式(20)和式(21)分别为各粒子赋初值。
步骤5)利用PSO 算法更新种群PPSO中各粒子的速度和位置,并利用式(19)对越界的粒子进行修正。同时利用DE 算法对种群PDE中各粒子执行选择、杂交、变异操作,并利用式(19)对越界的粒子进行修正。
步骤6)找出种群PPSO和PDE中的最优个体A1=
步骤7)计算并比较a1=θ(A1)和a2=θ(A2)的大小,选择适应度值小的个体进入下一代。
步骤8)判断个体适应度值是否满足条件或者算法已达到最大迭代次数,若是,则输出个体最优适应度值,否则,继续执行迭代。
步骤9)程序结束,输出全局最优解。
3 算例分析
以西北地区某风电场为例进行仿真分析,该风电场装机容量为100 MW,通过计算其最优储能容量来验证本文提出风电场储能容量优化配置计算方法的正确性和实用性。该风电场2021 年风功率变化情况如图1所示。

图1 风电场2021年风功率变化情况
设置调度周期为1 年,即T=8 760 h,调度时间窗口Δt=1 h,风功率波动约束的可信度水平ξ=0.95[20]。风电场中配置的储能蓄电池参数如表1所示。

表1 蓄电池参数
在MATLAB 中编制计算程序,利用改进PSO-DE融合算法对风电场优化配置模型进行求解,改进PSO-DE 融合算法的迭代过程如图2 所示,为了对比分析,图2 中同时给出了PSO-DE 融合算法的迭代过程,由图2 可知,改进PSO-DE 融合算法找到最优解时所需的迭代次数更少,求解精度更高。

图2 两种算法的迭代过程
表2 给出了两种优化算法的优化结果。由表2可知,相比PSO-DE算法,改进PSO-DE融合算法的迭代次数、收敛时间和最优解分别为48 次、0.58 s 和624.18万元,均优于PSO-DE 算法,可见PSO-DE 融合算法提高计算精度,加快算法收敛,同时也验证了所提改进策略的正确性。

表2 两种优化算法的优化结果
当目标函数取得最小值时,对应的最优储能容量为11.25 MWh,风电场弃风率为0.15%。图3 给出了风电场弃风率随储能容量变化的过程,由图3 可知,当风电场储能容量小于11 MWh,随着储能容量的增大,弃风率迅速减小,风能利用率明显增大;当风电场储能容量超过11 MWh,随着储能容量的增大,弃风率缓慢变小,直到储能容量达到20 MWh 左右时,风能利用率达到最大,不再随着储能容量而变化。

图3 弃风率变化曲线
图4 给出了有功功率偏差随储能容量变化的过程,由图4 可知,随着储能容量的增大,风电场输出功率的有功功率偏差逐渐减小,可见储能设备使风电场输出功率更平滑,越接近风功率的参考出力,当风电场储能容量超过11 MWh后,储能容量的增大已无法抑制风电场输出功率的随机波动。因此综合考虑储能成本、弃风率和风功率平滑效果,该风电场的最优储能储量为11.25 MWh。

图4 有功功率偏差变化曲线
求解出风电场最优储能容量后,对风电场配置储能蓄电池后的平抑效果进行验证,2020年1月1日08:00 至20:00 的风电输出功率变化情况和经过储能蓄电池平抑波动后的输出效果如图5 所示。从图5可以看出,在风电场配置11.24 MWh的储能蓄电池后,风电场输出功率波动明显减小,功率输出更平稳,平抑风功率波动效果明显。
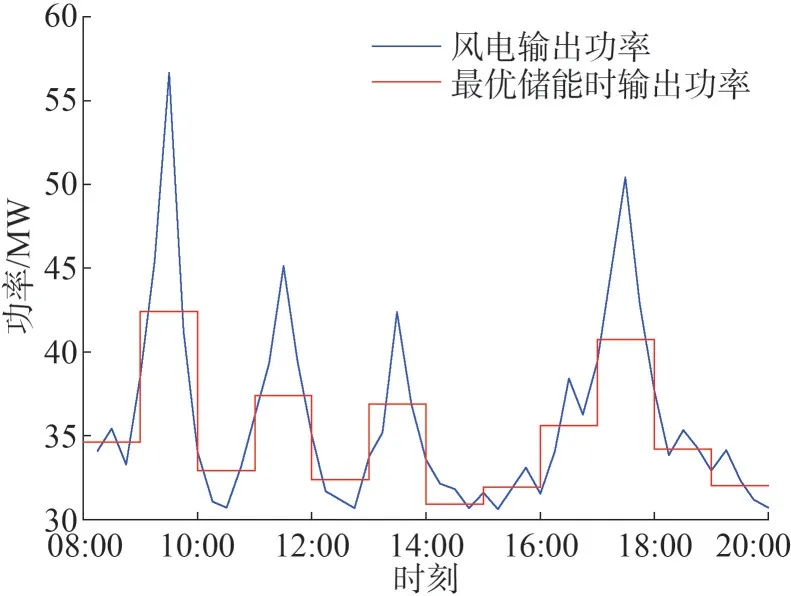
图5 风功率预测值及最优储能时风电场输出功率
4 结语
将蓄电池作为风电场储能设备,对风电场储能容量优化配置进行研究,综合考虑蓄电池投资成本和风电场弃风率,建立了由蓄电池投资成本和风电场弃风率组成综合成本为目标函数的风电场储能容量优化配置模型,采用惯性权系数调整、越界粒子变异操作和粒子初始化规则调整等策略对PSO-DE 算法进行改进,提高了PSO-DE算法的计算精度和收敛性能,并利用实际风电场运行数据进行了算例分析,结果表明,改进PSO-DE 融合算法只需要48 次迭代就找到了综合成本最小值为624.18 万元,对应的最优储能容量为11.25 MWh,风电场弃风率为0.15%,验证了本文提出的风电场最优储能容量计算方法的实用性。
