基于氢储能的可再生能源系统协同规划方法
2023-02-19刘学智
高 源,刘学智
(1. 上海交通大学 电子信息与电气工程学院,上海 200240;2.贵州电网有限责任公司 电力科学研究院,贵阳 550002)
0 引言
建立高渗透率可再生能源系统是实现碳中和的必由之路。在实现高渗透率可再生能源的道路上,存在诸多问题尚待解决,一方面,风力发电与光伏发电具有低碳、经济、环保的优点,被广泛运用高渗透率可再生能源系统,但风光发电存在间歇性、随机性、难以控制等特点,且呈现日内及季节性波动的特性[1]。另一方面,由于传统燃煤、燃气机组的高碳排放,难以适应高可再生能源渗透率的电力系统。氢储能在长时间存储与多能源耦合具有很大优势,具有潜力成为平抑跨周、跨季节与跨部门能量平衡的重要储能类型[2],如何利用氢储能成为提升高渗透率可再生能源系统可靠性与经济性的必要技术。
在可再生能源出力不确定性处理方面,目前国内外针对可再生能源与储能协同规划方面的研究主要面向微网中的多能互补系统[3—5],基于典型的每日出力场景展开计算,未能充分考虑可再生能源出力的季节性特征。文献[4]根据对风电季节特征的分析,生成风电初始场景并运用向后选择算法对场景进行缩减。在此基础上,对基于场景法的IES规划过程。文献[5]构建了考虑多重不确定性因素的分布式电源鲁棒规划模型。基于场景法的研究在场景缩减时可能导致极限场景的丢失,基于鲁棒优化模型的研究建模和求解过于复杂且难以理解。针对该问题,有研究利用全年时序生产模拟的方式对可再生能源的容量计算[6]。全年时序生产模拟通过逐小时的可再生能源出力为输入,不仅充分考虑可再生能源的日内随机性与互补性,也能体现出可再生能源的季节性特征。文献[7]研究计及电力系统灵活性基于时序曲线的运行模拟模型方法和储能需求分析流程,统筹优化系统目标水平年的储能结构及容量。根据有关欧洲风光储互补发电系统储能配置的研究,风电发电量占比为60%,光伏发电量占比为40%时,能抵御季节性的依赖,当配置完全为光伏发电或风力发电时,所需储能的容量将剧增[8]。因此,通过全年时序生产模拟的方式合理规划各种可再生能源比例能有效抵御可再生能源季节性波动的影响[9]。
针对长时间尺度下储能配置方面,现有研究针对高渗透率可再生能源系统的规划中大多考虑在系统中配置电池储能[10],少有文献能综合考虑蓄电池在寿命、成本、环境污染等方面的劣势,此外电池储能属于短期储能,并不适合跨季节性存储。氢储能技术作为具有巨大潜力的季节性储能,能够实现大规模能量转移与功率支撑能力,对环境友好,能量密度高,存储时间长,成为未来电力系统中最主要的储能方式[11—12]。文献[13]简要描述风-氢耦合系统相关概念和框架,结合国内外相关研究动态和成果基础上,对发展风-氢耦合发电技术提供了建议。文献[14]以风力发电公司为投资主体,探索风电场和电转气厂站的协同投资建设模式。文献[15—17]从电源类型的层面规划各类型电源的扩展容量,建立了计及氢负荷的电源规划模型。当前关于氢储能的研究主要着眼于氢能的调度运行、提高可再生能源的消纳。氢储能相对电池储能的优势在于成本低,能够实现每日、周、季节的能量转移,但也存在储能效率低的劣势,应合理配置的储能容量、优化规划策略,提升整个系统的经济性。此外,很少研究能充分对比基于氢储能系统与基于电池储能的可再生能源系统规划优劣性。
综上所述,已有大量关于计及储能的可再生能源系统的研究,但尚无研究针对长时间尺度下基于氢储能的可再生能源系统规划与协同运行方法的研究,也尚未有研究考虑对比不同地区下不同储能类型系统规划成本等多方面因素。本文建立了基于氢储能的可再生能源系统协同规划模型,将系统成本问题与运行模拟问题统一到规划层面,使制—储—用氢纳入可再生能源规划决策。以最小年化成本为目标函数验证基于储能系统的经济性,根据具有不同风光资源特性的两地区风光数据进行算例分析,并对比了本文提出的系统与基于电池储能的可再生能源系统的转化效率、经济性、弃电率等参数。最后,引入可调度能源(dispatchable energy,DE)价格与电解槽设备输入功率变化量对系统参数的灵敏度分析。
1 基于氢储能的可再生能源系统协同规划模型
1.1 系统总体架构及思路
本文所对比的基于传统电池储能的可再生能源系统和基于氢储能系统的可再生能源系统结构如图1 所示。可再生能源发电系统由光伏发电系统、风力发电系统互补发电。电池储能系统选择目前最为常见的锂电池,整个氢储能系系统由电解槽、储氢罐、压缩机和燃料电池组成。氢储能系统利用电解槽将电能转化为氢气通过压缩机储存到储氢罐中,储氢罐中的氢气通过燃料电池将氢气转化为电能给系统供电。
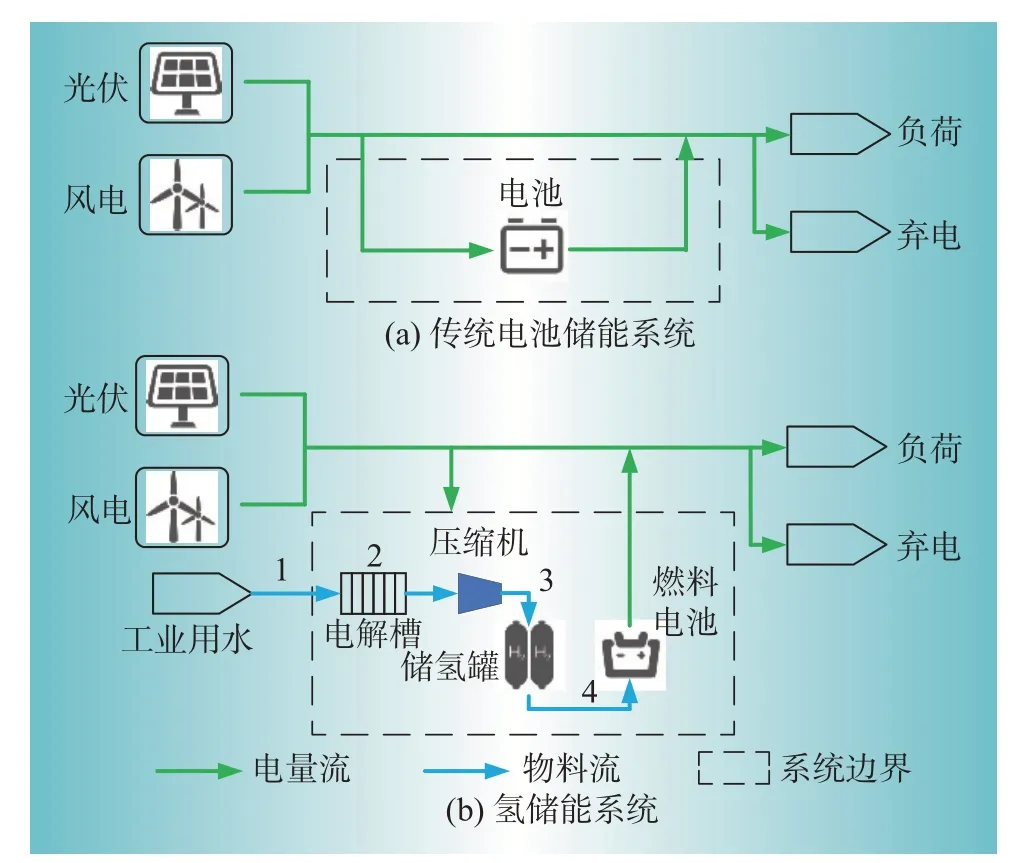
图1 两种类型储能模型的系统结构Fig.1 System structure of two types of energy storage models
文章的总体思路如图2 所示,首先输入可再生能源出力、负荷需求及系统各部分成本数据,将目标函数中非线性规划转化为线性规划问题优化求解,然后对比不同地区配置不同类型储能系统对输出量的影响,进一步分析氢储能系统的优劣性,最后引入可调度能源价格及电解槽功率变化量对系统进行灵敏度分析。

图2 总体思路Fig.2 General idea
1.2 可再生能源发电系统模型
可再生能源发电装置的容量系数(capacity factor,CF)反映了选用的可再生能源机组利用率的参数,定义为在分析期间内产生的总电量除以在此期间额定功率运行时产生的总电量
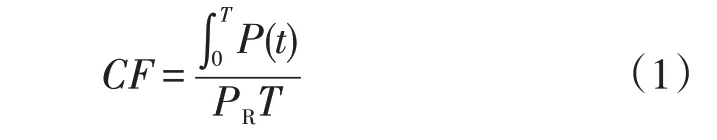
式中:CF为可再生能源发电设备容量系数;P(t)为发电机组在t时刻的功率;PR为额定功率;T为模拟的数据总时长。
可再生能源发电模型是基于风力发电与光伏发电的标准化数据表示出的,其定义为整个分析期间的累计发电量等于一年内的总负荷需求量[8]
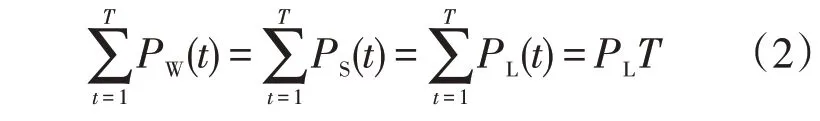
式中:PW(t)为t时刻风力发电机输出功率;PS(t)为t时刻光伏输出功率;PL(t)为t时刻负荷需求功率。
由于可再生能源具有间歇性,可再生能源发电量过剩不可避免,为了量化过剩发电量,引入了可再生能源渗透率γ,定义为可再生能源发电装置产生的总电量与总需求电量的比值:例如γ为2时,代表可再生能源发电总量是负荷需求总量的2倍。可再生能源输出功率可表示为
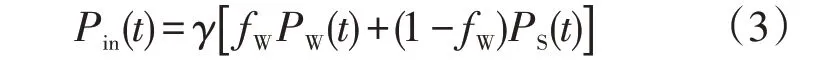
式中:Pin(t)为t时刻可再生能源输出功率;fW为可再生能源发电中风力发电的占比。由于本文仅考虑了两种可再生能源,因此光伏发电的占比用(1-fW)表示。
1.3 氢储能系统模型
目前最为常见、技术成熟度最高的储氢技术为压缩氢气储能。对系统的能量平衡方程进行建模
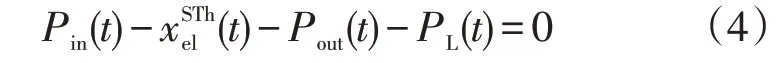
式中:x(t)为t时刻整个储氢系统中消耗的电量与释放电量,为正时为耗电、为负时为放电;Pout(t)为t时刻可再生能源弃电量;PL(t)为t时刻负荷需求。
电解槽电解水将电力转化为氢气和氧气,氢气压缩机消耗电力将产生的氢气储存进储氢罐中,当需要储氢系统供电时,利用燃料电池将氢气转化为电力,这一过程表示为
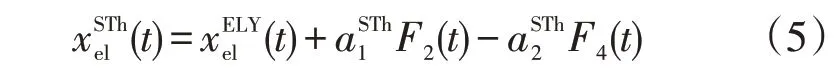
式中:x(t)为t时刻电解槽的运行功率;a为氢气压缩机压缩单位质量氢气耗电量(3.03 kWh∕kg);a为燃料电池的单位质量氢气的耗电量(22.28 kWh∕kg);F2(t)为氢气压缩机的氢气给储氢罐的氢气流量;F4(t)为储氢罐供给燃料电池的氢气流量。
如图3所示,由于电解槽的物理与化学特性,过去研究中常使用常数标准能耗比曲线,实际上能耗比呈非线性或线性函数,本文选择能耗比线性化函数,电解槽输入功率如下所示[18]
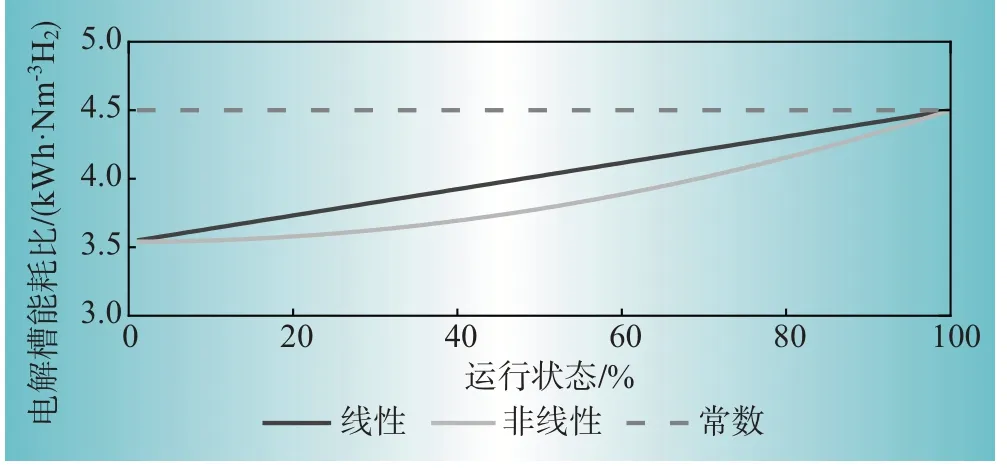
图3 电解槽的能耗比关系Fig.3 Energy consumption ratio of electrolytic cell
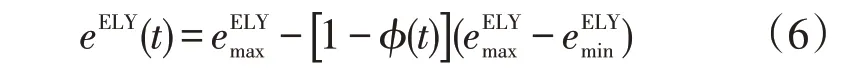
式中:eELY(t)为单位流量电解槽的耗电量;e为满载状态下的单位流量的耗电量,取4.5 kWh∕Nm3,为方便压缩氢气造成体积变化,用质量进行表征,相当于55.7 kWh∕kg;φ(t)为电解槽工作百分比率;e为空载状态下的耗电量,取3.54 kWh∕Nm3,相当于39.4 kWh∕kg。
通过物料衡算反映出系统化学转化过程中物料比例及物料转变的定量关系。储氢过程的物料衡算方程为


式中:F1(t)为电解槽电解水流量;MW.H2O、MW.H2分别为水与氢气的分子摩尔质量;F3(t)为经过氢气压缩器压缩后的氢气流量,由于忽略整个过程中的氢气损失因此对于每一时刻等于存在等式(9)。建立了储氢系统运行模型,表示两个相邻时刻储氢罐的容量时序关系
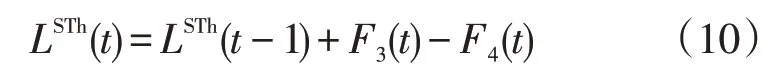
式中:LSTh(t)为经过储氢罐中t时刻的储氢量。
借鉴传统的蓄电池荷电状态(state of charge,SOC)的概念定义氢储能的SOC,保证储能设备的安全运行与使用寿命[19]。除满足SOC约束外,储氢还需满足最大储氢量、最大氢气流量、燃料电池最大消耗氢气流量约束以及全年产生氢气和消耗氢气总量约束

1.4 电池储能系统模型
文中所对比的电池储能系统由锂电池构成,根据设备的出力,建立电量平衡方程如下所示
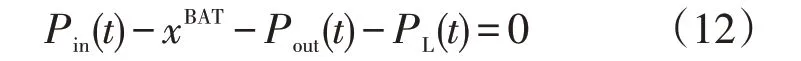
式中:xBAT为锂电池的充放电功率,其值为正时表示电池储能系统充电,为负时表示电池储能系统放电

式中:Pch(t)、Pdis(t)分别为t时刻储能的充放电功率。电池储能过程的能量状态方程为
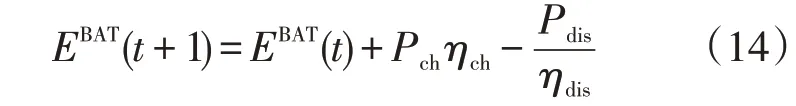
荷电状态约束:为减少过充过放对储能的使用寿命的影响,电池SOC与氢储能SOC都应当在合理的限定范围内;电池储能充放电约束:电池的输出功率需小于额定功率且不能同时充放电;初始与结束状态平衡约束:储能运行周期内的初始时刻与结束时刻的荷电状态相同。相关约束如式(15)所示

2 目标函数及评价参数
目标函数为系统的年化成本最低,对每个设备运行和容量规划进行优化,从而评估整个系统的经济性。系统的年化成本计算公式为

式中:CGEN为发电设备的年化成本;CELY为电解槽装置的年化成本;CSTh为储氢罐的年化成本;CFC为燃料电池的年化成本;CPW为工业用水年化成本。
发电设备的年化成本计算方法为

式中:i为不同类型的发电设备,为W 时代表风电、为S 时代表光伏发电;CFi为容量因子;fCR为投资回收系数;FCapEx为固定投资成本;FOpEx为运营成本。fCR计算公式为
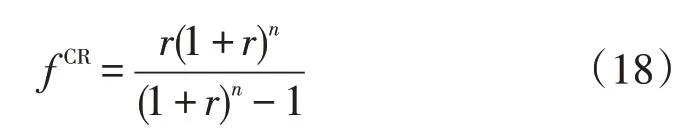
式中:r为贴现率;n为系统中元件的寿命。
电解槽、压缩机、储氢罐以及燃料电池的固定投资年化成本组成了氢储能系统的年化成本

工业用水年化成本为
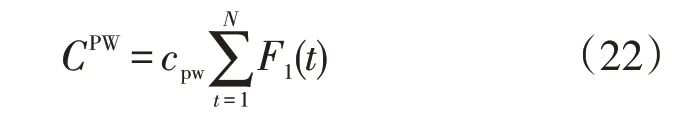
式中:cpw为工业用水的单价。
系统规划的目的是确定存储设备(电池、电解槽、储氢罐、燃料电池)及可再生能源输出功率的最佳规划容量及其运行方式,从而最小化系统年化成本。优化问题的约束条件除了受限于上文给定的约束外,还受制于以下的约束
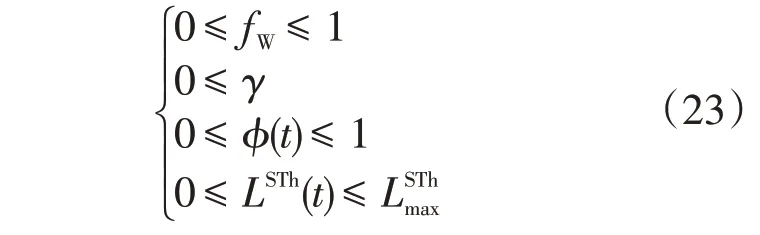
绿电比例指风力与光伏发电进入系统中的比例,用于评估系统的环保性

弃电率指标用于表征系统的可持续发展水平

式中:βcut为系统的弃电率。
3 算例仿真
本文所建立的基于氢储系统的数学模型为非线性模型,难以求解,将其转化易于求解的线性规划模型,基于电池储能的模型为混合整数线性规划模型,两种模型都利用GAMS软件优化求解。
3.1 算例数据
本文的算例数据采用上海某海岛(A),新疆某地区(B)两地区2019 年全年时间间隔为1 h 的历史天气数据转化为风光发电数据,验证所提方法的有效性。风力发电与光伏发电标准化后曲线如图4所示。对于A地区,风电CF值为0.329、光伏CF值为0.161,风电利用率大于光伏利用率;对于B地区,风电CF值为0.043、光伏CF值为0.250,光伏利用率远大于风电利用率;A 地区的风电利用率优于B 地区,而B地区的光伏利用率优于A地区。


图4 A,B两地区的标准化风光发电功率Fig.4 Standardized wind and solar power generation in regions A and B
两地区在2019 年标准化负荷需求如图5 所示,两地区负荷呈现出季节性分布,用电高峰在夏季,用电低谷在冬季,A地区负荷波动性大于B地区。
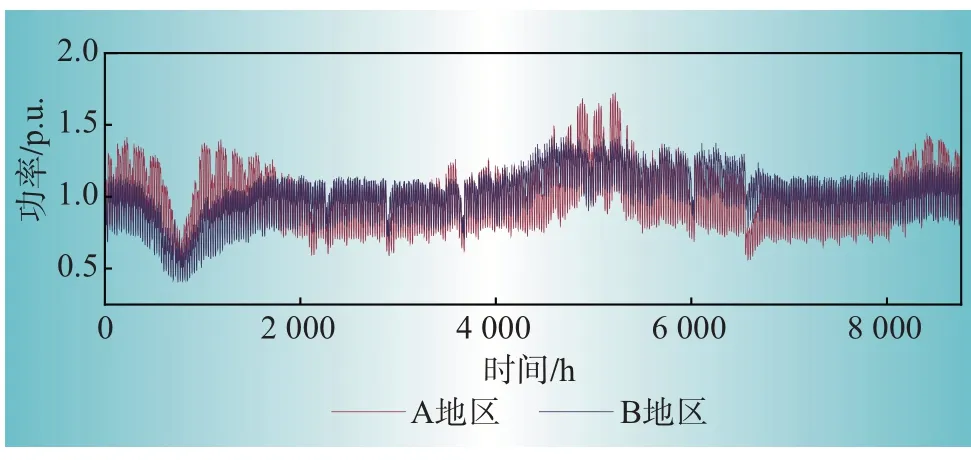
图5 A,B两地区的标准化负荷需求Fig.5 Standardized load demend in regions A and B
系统中各元件的相关参数如表1所示。

表1 各元件的相关参数Table 1 Related parameters of each component
3.2 不同类型储能系统的成本对比分析
为直观分析不同类型储能的系统在不同地区的规划结果,采用文中所提的两种储能模型对A,B两地区规划结果的成本进行分析,不同系统成本构成如图6 所示。从中可知无论在A 与B 地区,规划基于氢储能的可再生能源系统的年化成本都小于规划基于电池储能的可再生能源系统,表明了本文所提的规划模型的经济性。由于氢储能与电池储能不同储能方式,在A 地区规划基于氢储能的可再生能源系统的成本小于B 地区,而基于电池储能的可再生能源系统呈现出相反的结果。对于不同储能类型的系统在A、B两地的成本构成比例也不同,A地区规划基于两种储能的光伏、风电、储能成本基本相等,而在B地区风电成本为0,表明该地区不适合规划风电。

图6 不同类型储能在A、B两地区的年化成本对比Fig.6 Annual cost comparison of different types of energy storage in regions A and B
不同类型储能系统的规划参数对比分析如表2所示,对比了不同类型储能在A、B 两地区的参数。从表中可知系统在不同地区规划的可再生能源渗透率、风力发电量、弃电率、储能的最大充放电功率∕最大氢气质量、储能容量参数不同。对于氢储能系统,A地区可再生能源渗透率小于B地区,而储能容量大于B地区,系统能够更好消纳可再生能源,使弃电率小于B 地区;对于电池储能A 地区可再生能源渗透率大于B地区,而储能容量小于B地区,导致弃电率较小,氢储能电池的弃电率远小于电池储能。对于两种储能方式A 地区的风电占比分别为62.12%与60.27%,B 地区的风电占比同为0%,说明A地区适合风光互补发电,而B地区由于风电CF远小于光伏CF,导致风电的成本较高,全部由光伏发电提供较优。对于氢储能系统的可再生能源弃电率都小于电池储能系统,说明规划氢储能有效减少可再生能源弃电率。通过计算系统储能装置充电总量除以放电总量得到氢储能与电池储能效率的转化效率,由于电解槽的电耗比曲线呈现线性分布,两地区电解槽工况不同,A地区氢储能转化效率大于B 地区,对于电池储能在A、B 地区转化效率都保持恒定,氢储能转化效率低于电池储能。

表2 不同类型储能在A、B两地区的参数对比Table 2 Parameters comparison of different types of energy storage in regions A and B
不同类型储能在A、B 地区的SOC变化量如图7所示。由于不同地区所需配置的风电、光伏、储能容量不同,导致不同时刻风电、光伏出力不同,氢储能系统及电池储能系统在配合充放能的策略也不同。在A地区,氢储能SOC变化量呈现出季节性,电池储能SOC呈现出频繁波动的特性,氢储能SOC变化幅度小于电池储能。对于B 地区,由于该地区在经济性最优规划下,光伏发电量占比为100%,两种储能的SOC变化都表现出波动频率大。两地区不同储能的SOC都在0.1~0.9之间波动保证了储能系统运行的安全性。
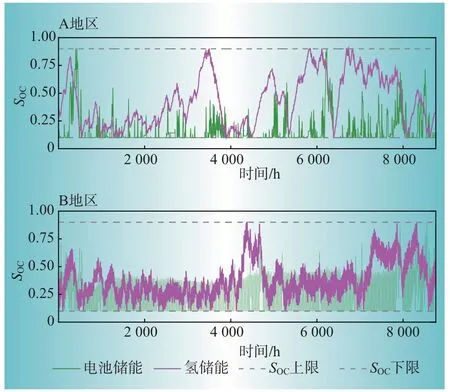
图7 A,B地区不同储能类型的SOCFig.7 SOC of different energy storage types in regions A and B
3.3 灵敏度分析
(1)可调度能源价格灵敏度分析
系统规划在于平衡绿电比例、弃电率以及经济性3 要素,对于不同的系统3 重要素的优先级是不同的。研究3重要素的影响关键在于分析不同要素之间的关系,上述分析主要关注该系统的经济性,尚未考虑引入可调度能源。本小节研究允许系统中引入可调度能源,发掘经济性、绿电比例以及弃电率3者的变化。将公式重新改写为
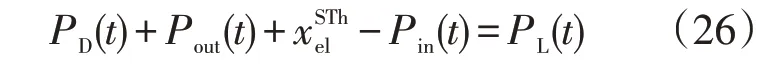
式中:PD(t)为t时刻可调度能源功率。假设可调度能源的成本为350~17 500 元∕MWh 时,研究系统的相关参数的变化。
图8显示了可调度能源价格对A地区储氢罐容量、绿电比例、弃电率以及年化成本的影响。年化成本与绿电比例随着可调度能源价格的增大而增加,弃电率与储能容量并没有随着可调度能源的价格一直递增,而是先增加到一定值后,稍微减小直到趋于稳定。当可调度能源价格小于350元∕MWh,规划风光发电设备及储能对系统并不是最优选择,系统全部由可调度机组发电。当价格大于15 750元∕MWh,由于引入可调度能源对整个系统不再具有经济性,此时系统将完全使用可再生能源,导致上述4 个参数均不再变化。

图8 可调度能源价格对A地区参数影响Fig.8 Influence of the price of dispatchable energy on the parameters of region A
(2)电解槽输入功率变化量灵敏度分析
由于电解槽电解水是一个缓慢的化学过程,需要考虑电制氢设备输入功率变化量,本小节研究对电解槽设备输入功率变化量对系统参数的影响,结果在低电解槽设备输入功率变化量下需要配置风电增加系统经济性。
图9显示了A 与B 两地区电解槽设备输入功率变化量对年化成本的影响,A 地区年化成本基本保持不变,B 地区随电解槽设备输入功率变化量的增加而急剧减小,表明了对于具有不同风光资源的地区,电解槽设备输入功率变化量对年化成本的影响差异巨大。
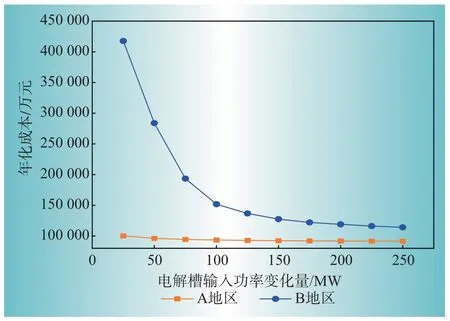
图9 电解槽输入功率变化量对A,B地区年化成本的影响Fig.9 Influence of limit of input power variation of electrolytic cell on annual cost in region A and B
4 结论
从实现未来高渗透率可再生能源出发,考虑可再生能源的日内与季节性波动,提出全年时序生产模拟的基于氢储能的可再生能源系统协同规划方法。对比上海某海岛与新疆某两地区的基于氢储能的可再生能源系统模型与基于电池储能的可再生能源系统所需配置装置参数、弃电率、储能效率及年化成本。最后对引入可调度能源价格与电解槽设备输入功率变化量对系统进行灵敏度分析。所得主要结论如下:
(1)氢储能系统转化效率上低于电池储能系统,但是在经济性与弃电率上具有优势。
(2)不同地区规划的结果不同,风光互补发电并不一定能增加经济性,在制定规划方案时,因地制宜选择适合该地区的规划方案。
(3)随着可调度能源价格增加,系统的年化成本、绿电比例、氢储能容量呈现上升趋势。
(4)系统的年化成本随着电解槽设备输入功率变化量的增加而减少,达到一定值时,不再变化。对于具有不同风光资源的地区,系统相关参数及年化成本受其影响差别巨大。D
