陶瓷研磨球直径对其磨耗性能的影响
2023-02-19夏维煌杨海涛张军恒唐涛李俊国沈强
夏维煌,杨海涛,,,张军恒,唐涛,李俊国,沈强
(1 广东佛山市陶瓷研究所控股集团股份有限公司,佛山 528300;2 萍乡市金刚科技工业园有限公司,萍乡 337022;3 武汉理工大学材料复合新技术国家重点实验室,武汉430070)
1 前言
陶瓷研磨球主要用在球磨机中进行物料粉碎研磨,其具有高硬度、适中密度、耐磨、耐腐蚀以及无金属杂质污染等重要优势,在建筑卫生陶瓷、水泥、矿山、电子材料、磁性材料、油漆、化妆品、食品、制药等工业中广泛使用[1-5]。
磨耗性能代表的是陶瓷研磨球的使用寿命,是陶瓷研磨球关键性能指标之一。根据现有行业标准[6],磨耗性能指标包括耐磨系数和当量磨耗两种。其中耐磨系数指的是单位时间失重百分比,有明确的物理意义。但在实际测试中发现耐磨系数受到陶瓷研磨球直径极大影响,并不能本征表达其磨耗性能。为了本征表达磨耗性能,耐磨系数被乘以直径及相关系数而逐渐演变成当量磨耗,其为无量纲量。但随着陶瓷研磨球向高耐磨方向发展,当量磨耗也逐渐受到直径的影响,无法本征表达其磨耗性能。因此目前是直径20 mm 以内的小球以耐磨系数来表征其磨耗性能,直径20 mm 以上的大球则以当量磨耗来表示。
鉴于当前陶瓷研磨球直径对磨耗测试性能影响显著,行业标准的测试效率不能满足企业大批量产品检测需求。新型高效磨耗检测方法逐渐受到重视。实验室快速球磨法是其中之一[7],其采用高转速(转速通常在400转每分钟以上)的工况来强化磨损,使得磨耗性能检测效率相比于常规检测显著提高。球的直径(代表体积和质量)越大,随之而来的冲量会显著增加,大直径的陶瓷研磨球具有极大的撞碎球磨罐的实验风险。通常该种方法适用于小尺寸(通常直径20mm 以内)研磨球或微珠,并且与小球的高转速的实际工况有些接近。
本文将在现有行标基础上研究研磨球直径对不同表达方法的磨耗性能的影响,以期寻找到磨耗性能的更合理表征,如此可以显著的提高测试效率。除了上述行标所述的耐磨系数、当量磨耗、还有类似的单位面积磨损量(下称面积磨耗并推导给出计算公式)表示方法本文将一并对比研究。
2 试验方法
2.1 实验材料
采用某些公司生产的如下规格的陶瓷研磨球为研究对象,相关参数如表1。

表1 陶瓷研磨球的基本信息
2.2 实验步骤
采用内径200 mm、内长220 mm 的聚氨酯球磨罐,装入4 kg 研磨球和2 kg 石英砂(40-60 目之间)和4 kg清水,其中石英砂的加入更好的模拟球磨工况。以80 转每分钟转速在球磨试验机上球磨24h,记录研磨球在球磨前后的质量,按下列公式计算磨耗。重复测试3 次取平均值。

式中,Y1为耐磨系数,单位为g kg-1h-1;
Y2为当量磨耗,单位无量纲;
△m 为研磨球球磨前后质量差值,单位为g;
m 为研磨前的质量,单位为g;
△t 为球磨时间,单位为h;
K 为修正系数,4.17×10-4,单位为mm-1;
D 为研磨球直径,单位为mm;
另外面积磨耗定义为单位面积单位时间的磨损量,也即

式中,Y3为面积磨耗,单位为g m-2h-1;S 为所有研磨球的总表面积,单位m2。
对于单颗研磨球,其体积V0和表面积S0如公式

因此总的研磨球的数量N 为

式中ρ 为研磨球密度,单位为g cm-3;研磨球总表面积S 为

将方程(7)代入方程(3)中,得到最终的面积磨耗公式(8)。

3 结果与讨论
3.1 直径对耐磨系数的影响
图1 给出了陶瓷研磨球的耐磨系数随直径的变化趋势。从图中可以看到,陶瓷研磨球Q1 的耐磨系数随直径有明显的衰减。对于耐磨系数稍小的陶瓷研磨球Q2,其衰减幅度变小,对于耐磨系数更小的陶瓷研磨球Q3,仍然可以看到其随直径衰减的现象,在耐磨系数衰减至0.17 g kg-1h-1后,直径的影响才不明显。
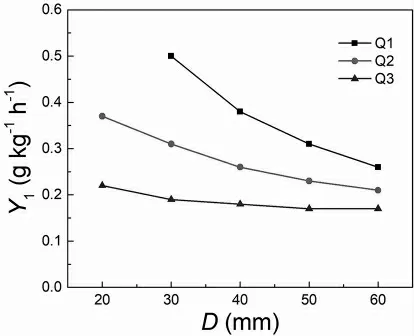
图1 陶瓷研磨球的耐磨系数随直径的变化趋势图
3.2 直径对当量磨耗的影响
图2 给出了陶瓷研磨球的当量磨耗随直径的变化趋势。从图中可以看到,所有样品的当量磨耗与直径呈现出线性关系。三种球磨耗最大的研磨球Q1,其当量磨耗随直径变化不大。在球磨粉碎行业中,早期的陶瓷研磨球是天然鹅卵石等石材基础上发展而来,其磨耗性能相比于鹅卵石有较大的提高,但当量磨耗相比于当前产品仍然偏高,研磨球Q1 就是典型代表。陶瓷研磨球Q1的当量磨耗随直径变化不大的规律也是行业标准中采用当量磨耗的缘由之一。对于磨耗性能稍好的陶瓷研磨球Q2,其当量磨耗随直径线性增大,对于耐磨系数更小的陶瓷研磨球Q3,线性增大的趋势更明显。
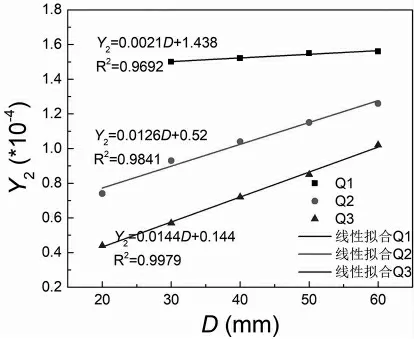
图2 陶瓷研磨球的当量磨耗随直径的变化趋势图
3.3 直径对面积磨耗的影响
图3 给出了陶瓷研磨球的面积磨耗随直径的变化趋势。从图中可以看到,三种陶瓷研磨球的面积磨耗呈现的规律与当量磨耗是一致的。对比公式14 和面积磨耗的计算公式8,可以推导出它们的关系为公式9。显然符合图3 所示规律。由于当量磨耗是无量纲的物理量,而面积磨耗的物理意义是单位面积单位时间的磨损量。因此可以考虑将面积磨耗等效为当量磨耗的物理意义。
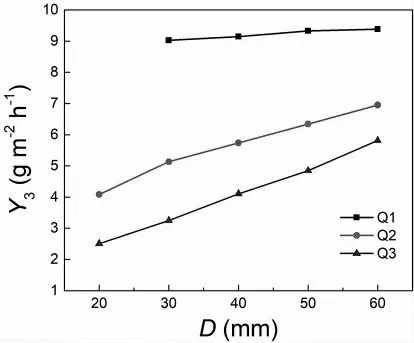
图3 陶瓷研磨球的面积磨耗随直径的变化趋势图

4 讨论
研磨球在实际球磨过程中同时包含了撞击引起的冲击磨损和表面摩擦引起的磨剥磨损[8-10]。冲击磨损与磨球的质量成正比,磨剥磨损与研磨球表面积成正比。相关公式推导如下。可以看到冲击磨损(公式11)与直径无关,而磨剥磨损(公式12)与直径成反比关系,对直径比较敏感。从推导出的耐磨系数理论表达式(13)可以看出,磨耗与直径呈现衰减趋势,这与图1 所示规律一致。
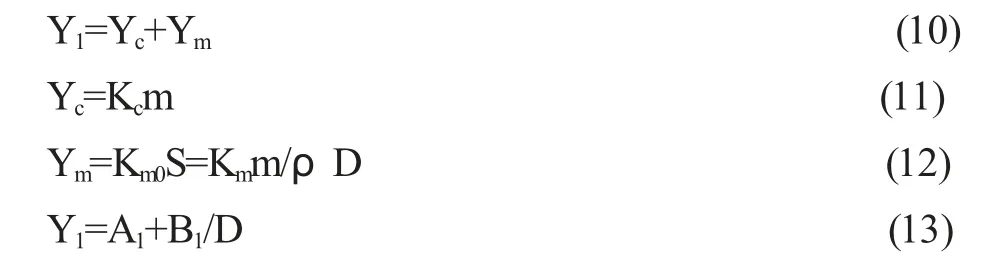
式中,Yc为冲击磨损,Ym为磨剥磨损;Kc、Km0、Km、A1、B1均为常数;其中A1=Kcm,B1=Kmm/ρ。
仔细推导当量磨耗的计算公式2 中修正系数K,其值为0.01/24,其中24 为测试时间(小时,h)。也即当量磨耗的计算公式可以改写成公式14,可以进一步推导出当量磨耗与耐磨系数的关系如公式15 所示。如此当量磨耗的最终理论表达式16 在公式13 基础上乘以D 推导而来。这与图2 所示规律一致。

从消除直径对磨耗性能测试结果的影响的角度出发,只有当磨剥磨损机制占比很小至可以忽略时,冲击磨损机制占据主导地位时,耐磨系数更适合批量表征。反之,当磨剥磨损机制占据主导地位时,当量磨耗更适合批量表征。对图2 中数据进行线性拟合,可以得到相关常数(表2)。可进一步对耐磨系数实验数据解析,可以得到冲击磨损机制和磨剥磨损机制的各自贡献(表3)。对直径敏感的磨剥磨损机制占比如表4 所示。可以看到不耐磨的样品Q1 的磨剥磨损机制占据主导地位(占比超过90%),此时当量磨耗有利于提高测试效率。而高耐磨的陶瓷球如样品Q3 的磨剥磨损机制不占主导地位,但其仍有相当占比。此时当量磨耗和耐磨系数都不适合批量表征。但其意味着陶瓷球继续向高耐磨发展至磨剥磨损相对可忽略时,耐磨系数则适合批量表征。

表2 陶瓷研磨球的磨耗性能相关常数
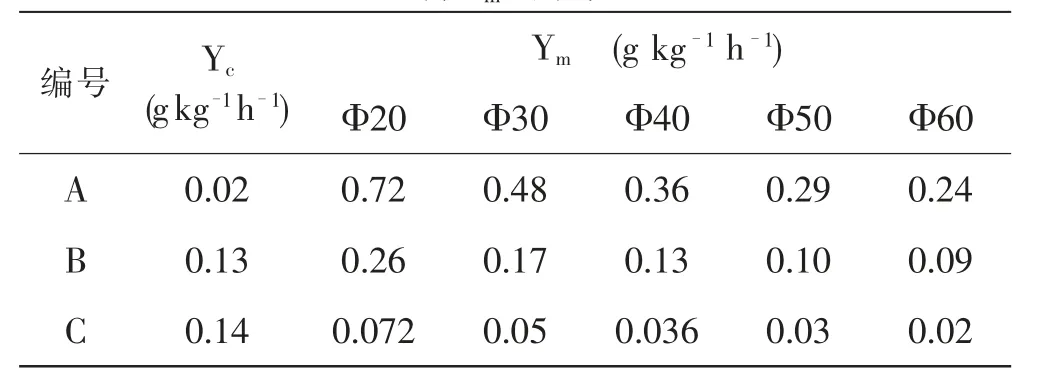
表3 陶瓷研磨球的冲击磨损机制Yc 和磨剥磨损机制Ym 的磨耗
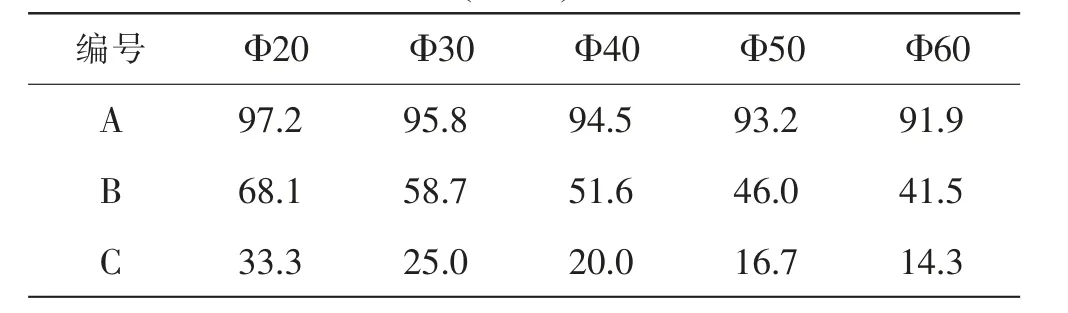
表4 陶瓷研磨球的磨剥磨损机制的占比(Ym/(Yc+Ym),%)
5 结论
本文探究了陶瓷研磨球直径对其磨耗性能的影响并对比了不同磨耗表征方法。得到如下结论:
(1)耐磨系数随着研磨球直径增大呈现衰减趋势。其衰减趋势是磨剥磨损机制贡献的。高耐磨产品的磨剥磨损机制占比低,意味着陶瓷球继续向高耐磨发展至磨剥磨损相对可忽略时,耐磨系数适合批量表征。
(2)当量磨耗随着研磨球直径增大呈现线性增大趋势。只有当磨剥磨损机制占比超过90%,此时冲击磨损机制可忽略,当量磨耗有利于提高测试效率。不耐磨产品的磨剥磨损为主要机制构成,当量磨耗适用于这种产品的批量表征。
(3)面积磨耗的物理意义是单位面积单位时间的磨损量,可等效为无量纲单位的当量磨耗的物理意义
