带电微粒在滤膜附近的定向运动*

周宏伟 欧阳文泽 徐升华2)†

1)(中国科学院力学研究所微重力重点实验室,北京 100190)

2)(中国科学院大学工程科学学院,北京 100049)

滤膜在过滤和分离领域具有非常广泛的使用,但滤膜对溶液中的组分具有吸引或排斥作用,导致粒子产生定向运动,进而在膜附近产生粒子富集或“粒子禁区”等截然不同的效应,目前对此认识尚不清楚,粒子浓度分布不能实时准确测量是其中最大的困难.本文以表面带负电荷的胶体粒子为模型物质,利用胶体粒子结晶后粒子浓度可以实时原位测量的优势,研究了纤维素滤膜对粒子运动行为的影响规律.研究结果发现带电微粒会自发地在滤膜表面产生富集,滤膜中微量阴阳离子释放导致的扩散泳效应是微粒朝向滤膜产生定向运动的主要原因,基于扩散泳和粒子扩散两种机制构建了粒子运动方程和模型,数值计算结果和实验结果定性一致.此外,粒子除了朝向滤膜的纵向运动之外,壁面电渗流和横向扩散还会使粒子朝向壁面产生迁移,导致管壁粒子数的增多.

1 引言

滤膜使用方法简单、过滤分离精度高,在生物医药工程、食品卫生、化工能源以及环境保护等领域受到了广泛的关注和使用.在外界能量或化学位差的推动下,滤膜可以使小于孔径尺寸的粒子或带电荷的分子透过膜孔,剩余部分则被截留下来,从而实现对两组分或多组分混合物的分级分离、提纯和浓缩富集.再生纤维素膜是一种在蛋白质分离纯化、血液透析等方面广泛使用的滤膜,具有亲水性和生物相容性好、可降解、渗透性和热稳定性高、低毒性等优点[1-4].但是在实际过滤过程中,由于蛋白质与滤膜之间的相互作用会显著降低样品的回收率,这种损失对于一些贵重蛋白质的分离和提纯是无法接受的.因此,研究溶液中带电微粒在滤膜影响下的运动行为,对于减小过滤过程中目标物质的损失,避免滤膜膜孔的堵塞具有重要的实际应用价值.

滤膜对溶液中分散物质的影响较为复杂,不同情况下会产生吸引或排斥作用,导致溶液中粒子的定向运动,进而在膜附近产生粒子富集或“粒子禁区”等截然不同的效应,目前对此认识尚不清楚,滤膜的离子效应、滤膜和颗粒之间的静电作用等都会对粒子的运动行为产生显著影响.

在滤膜的离子效应方面,由于滤膜制备过程中的化学反应或者滤膜自身材质问题,使得滤膜中残留有微量的阴阳离子,有些离子可以通过清洗去除,有些离子是化学键合在膜上的,只要和溶液接触,就会有离子释放和离子扩散.如Florea等[5]发现Nafion 滤膜和胶体粒子在溶液中接触后,胶体粒子会从滤膜-水的界面上被排斥数百微米,从而在滤膜表面附近形成“粒子禁区”,滤膜中的氢离子(来源于膜成份中磺酸基的电离)与溶液中的钠离子之间的离子交换导致的扩散泳效应可能是其主要原因.基于此现象,Lee等[6]制备了微流控器件用于无动力驱动的水净化装置;Chen等[7]在微流体通道内,实现了样品的混合、分离和定向引导.但是,Esplandiu等[8]进一步研究发现,并非所有粒子都会远离滤膜形成“粒子禁区”,还和粒子表面带电性质有关,只有表面带负电荷的粒子可以,而带正电的粒子运动方向相反,会在滤膜表面富集.滤膜的离子效应和粒子表面带电性质共同决定了粒子的运动方向.

滤膜和粒子间的静电作用是另一个不可忽视的影响因素,由于滤膜表面荷电基团在水溶液中的电离或者对溶液中离子的特异性吸附,滤膜表面通常带有电荷,会和溶液中的带电物质产生静电排斥或吸引作用.例如Oh等[9,10]研究了聚酰胺滤膜对带正、负电荷及中性纳米粒子的影响,发现静电作用是粒子运动和滤膜污染的主要原因,正电荷粒子被滤膜吸引加速滤膜的污染,负电荷粒子被滤膜排斥减轻污染.Zhang等[11]通过在滤膜上接枝电中性的两性离子聚合物,降低了滤膜表面的zeta 电势,可以显著降低静电作用导致的膜污染.Singh和Song[12]发现粒子的zeta 电势随着溶液pH 值的增大而增大,滤膜受污染程度和粒子zeta 电势呈现负的线性相关,而和溶液离子强度的自然对数值呈现正的线性相关,其原因在于pH 值的增大会增强粒子间的排斥力,而离子强度的增强会屏蔽粒子表面电荷,压缩粒子双电层厚度,降低粒子间的排斥力.除此之外,溶液中电解质浓度、电解质种类等也会对滤膜附近粒子的运动行为有影响[13-15].

以上这些研究表明,由于滤膜成分以及物理化学性质上的差异,滤膜和溶液中物质的相互作用机制亦不相同,进而会对溶液中带电微粒的运动行为以及后续的分离效果产生截然不同的影响.本文研究了再生纤维素膜对带电聚苯乙烯(PS)胶体粒子在溶液中运动行为的影响.之所以选择带电胶体粒子,主要基于以下两个方面的考虑:第一,胶体粒子可以视为蛋白质或污染物的原型,二者在大小和带电情况方面类似;第二,胶体粒子浓度可以实时监测,胶体结晶(胶体粒子有序排列形成晶格结构)后形成的胶体晶体可以作为粒子浓度探测器,结合反射光谱分析技术可以在无外界干扰的条件下实时、原位地测量粒子的时空分布,这对于认识粒子运动规律和运动机制至关重要.

2 实验部分

2.1 实验材料

实验中所用的聚苯乙烯粒子由乳液聚合法合成,粒子表面带有磺酸基(R-SO3H),当粒子分散在溶液中时,磺酸基的电离会使得粒子表面带有负电荷.粒子的表面电荷数约为680,由电导率-粒子数密度法测得[16];粒子的直径和多分散指数由动态光散射仪(Brookhaven,BI-200SM,USA)测量,其结果分别为90 nm,0.06.滤膜采用的是管状微型透析管(Slide-A-Lyzer MINI Dialysis Units,Thermo Scientific)底部的再生纤维素滤膜,其截留分子量(MWCO)为3500 Da.

2.2 实验装置与实验方法

实验装置如图1 所示,反射光谱仪(Avaspec-2048,Avantes,Netherlands)光源发出的白光经过光纤传导后垂直照射到石英样品管(内径10 mm,长30 mm)上,由样品反射回来的光被光谱仪检测器接收得到反射光谱图.实验时,首先把经过离心纯化、脱盐的胶体粒子溶液注入样品管中,由于粒子间的静电排斥作用,胶体粒子会形成有序排列的液态胶体晶体.然后把微型透析管插入样品管中,使透析管底部的滤膜和样品管中的粒子溶液充分接触(t=0 h),随后用封口膜(parafilm)密封上下管之间的连接部分,防止水分蒸发和外部空气进入.最后,根据实验需求,在上面的透析管内注入粒子溶液或者纯水,并加盖密封.需要说明的是,由于后续这些操作导致的时间延迟,本文中反射光谱的首次测量时间t0约为0.2 h.

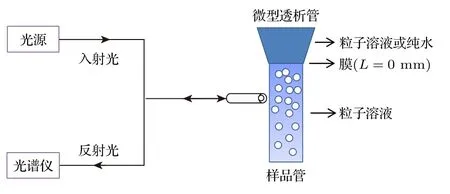
图1 实验装置示意图Fig.1.Sketch of the experimental setup.

样品管中粒子的空间分布由反射光谱光纤上下移动进行测量(滤膜的位置设定为L=0 mm,测量范围L=0.5—15.5 mm).反射光谱反射峰波长的变化可以转变为粒子体积分数Φ和粒子数密度n的变化[17,18]:

其中a为粒子半径,λ为反射峰波长,ν为溶液的折射率(νν粒子Φ+ν水(1-Φ)).

3 实验结果与讨论

3.1 粒子纵向运动和模型分析

图2 是样品(纯水-滤膜-粒子溶液)在t=0.2 h和t=31 h 时的反射光谱图,以及对应的反射峰波长分布和粒子体积分数分布.可以看出,t=0.2 h时在距离滤膜不同距离处,反射峰波长分布基本是一致的,均在765 nm 左右,表明开始时样品管中的粒子分布是均匀的(图2(a)和图2(c)),管内各处的粒子体积分数均和初始体积分数Φ0=0.012一致(图2(d)).但是,在滤膜的持续影响下,t=31 h 时管内样品反射峰的波长分布发生了很大的变化:样品中粒子的分布从初始的均匀分布变为不均匀分布(图2(b)和图2(c)),距离滤膜越近的地方,粒子体积分数越大,粒子越多,在靠近滤膜的一端和远离滤膜的一端,反射峰波长相差约200 nm,粒子体积分数相差约2.5 倍(图2(d)).

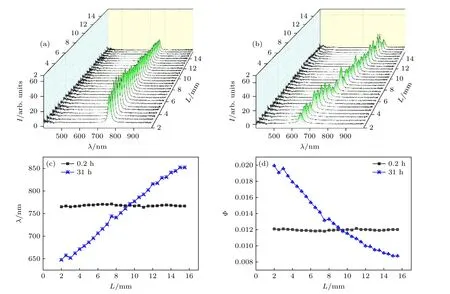
图2 (a)t=0.2 h 和(b)t=31 h 两个典型时刻的反射光谱图,以及与之对应的反射峰波长分布(c)和粒子体积分数分布(d)Fig.2.Reflection spectra at two typical time points(a)t=0.2 h and(b)t=31 h,and the corresponding peak wavelength distribution(c)and volume fraction distribution(d).

为了更加详细地研究样品管中粒子分布的动态演化过程,分别在不同时刻和不同位置对管内的粒子浓度分布进行测量,相关的Φ-L曲线和Φ-t曲线如图3(a)和图3(b)所示.需要说明的是,图3(a)中t=0.2 h的Φ-L曲线中没有L<2 mm 的数据,其原因是滤膜和样品溶液初始接触时产生的液面振动,使得滤膜附近的胶体晶体样品遭到破坏,反射光谱无法测量.但是随着静置时间的延长,该区域内的胶体粒子会重新结晶形成晶体,所以从t=1 h 开始以及后面的时刻,L<2 mm 的区域重新有了数据.

Φ-L曲线(图3(a))可以完整地反映整个样品管中不同位置处粒子浓度随时间的变化趋势,在不同时刻,Φ-L曲线表现呈现出不同的形状,说明管内粒子分布一直在发生演变.为了叙述方便,根据粒子浓度Φ和初始浓度Φ0之间的关系,将样品分为3 个区域:区域I,Φ＞Φ0;区域II,Φ<Φ0;区域III,Φ=Φ0.在t=1 h 时,粒子分布呈典型三区域:区域I(Φ＞Φ0,0—1.5 mm),区域II(Φ<Φ0,2.0—7.5 mm),区域III(Φ=Φ0,8.0—15.5 mm),表明此时滤膜的影响范围大约为7.5 mm.t=5 h 时,区域I(0—4 mm)和区域II(4—15.5 mm)的范围均逐渐扩大,区域III 消失,表明滤膜的影响已经遍及了整个样品区域.t=10 h 时,区域I继续扩大,区域II 持续缩小,区域III 消失.最终,在t=31 h 时,管内样品分布达到稳定,Φ-L曲线基本呈线性,此时区域I 的范围达到最大,区域II的范围达到最小,区域III 完全消失.

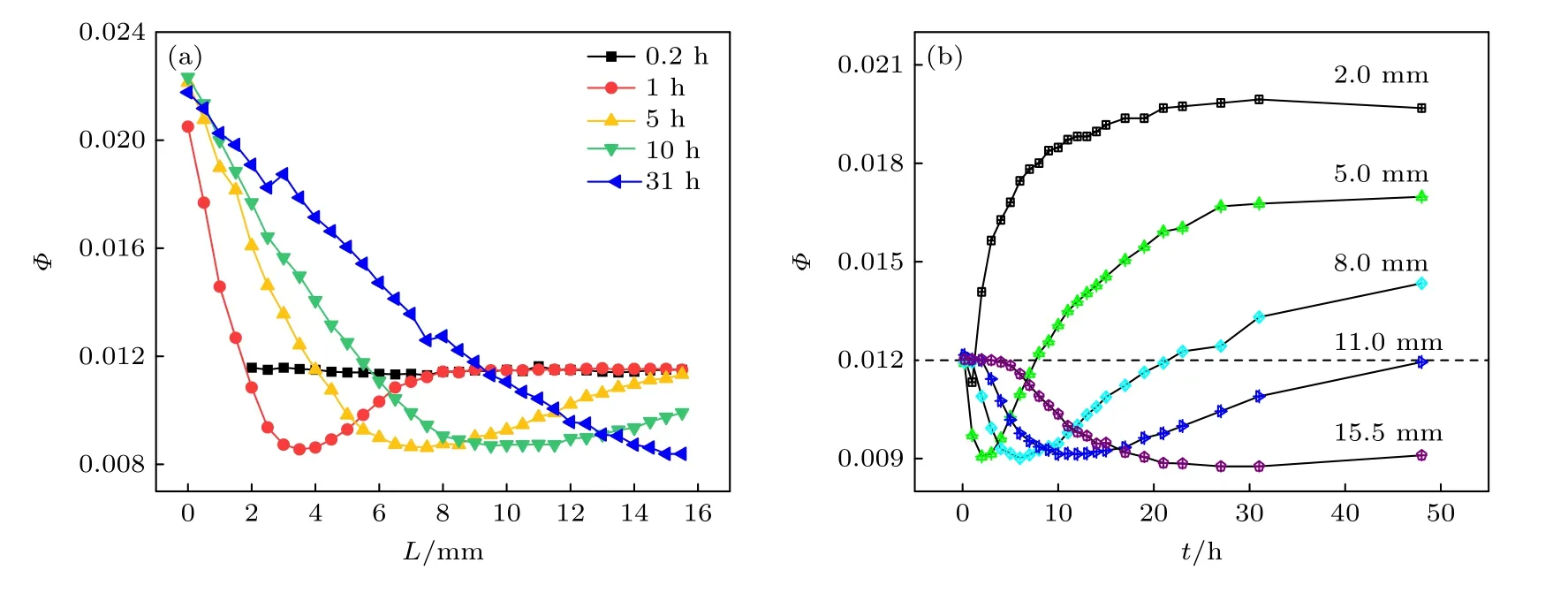
图3 样品管中粒子浓度分布的演变过程(a)不同时刻的Φ-L 曲线;(b)不同位置的Φ-t 曲线Fig.3.Particle concentration evolution in the sample tube:(a)Φ-L curves at different time points;(b)Φ-t curves at different locations.

Φ-t曲线(图3(b))反映了同一位置处粒子体积分数随时间的变化趋势.可以看出,Φ-t曲线也呈现不同的形状,大致分为3 类:第1 类,Φ-t曲线快速增长然后趋于平缓,表明粒子在持续、快速地增多,这类变化主要发生在距离膜较近的位置(L=2.0 mm);第2 类,Φ-t曲线先下降后增长(L=5.0,8.0,11.0 mm),表明这些位置的粒子数先减小后增大.曲线呈下凹形状意味着滤膜造成的定向迁移效应非常强烈,在很短时间内就会造成大量粒子朝向滤膜运动,粒子离开后的那部分空间由于得不到下方粒子的及时有效补充,所以形成了暂时的粒子亏空状态(Φ-t曲线下降),然后随着下方粒子的持续补充,区域内粒子数又得以重新增加(Φ-t曲线上升).第3 类,Φ-t曲线先保持不变然后持续下降并趋于平缓,这类变化主要发生在样品管底面附近(L=15.5 mm),在滤膜影响没有到达之前,粒子体积分数保持不变(Φ-t曲线不变),滤膜影响到达以后,粒子数开始缓慢下降,由于管底面处的粒子无法再得到下方粒子的补充,所以Φ-t曲线表现为持续的下降.以上实验结果表明,在纯水-滤膜-粒子溶液的体系中,溶液中的带电粒子会发生明显的、朝向滤膜的定向迁移运动.

粒子产生这种长距离、大范围定向运动的原因,首先可以排除膜表面带电特性的影响,因为静电作用范围主要集中于靠近滤膜表面的区域,不会引起整个样品池内粒子分布的变化.其次,考虑可能是滤膜两侧渗透压不一致所致.实验中所用的滤膜截留分子量为3500 Da,尽管道尔顿数和粒子大小没有明确对应关系,但技术资料表明3500 Da 的滤膜只能允许大约5 nm 以下的颗粒通过,滤膜孔径远小于实验中所用的胶体粒子直径90 nm,因此,滤膜上方的水分子可以自由穿过滤膜,而滤膜下方的粒子,虽有向上运动的趋势,但限于滤膜孔径,只能在滤膜附近富集.为此,将滤膜上方的纯水溶液更换为与滤膜下方完全一样的胶体粒子溶液,即粒子溶液-滤膜-粒子溶液.实验结果表明,粒子溶液-滤膜-粒子溶液(PP)体系和纯水-滤膜-粒子溶液(WP)体系中粒子浓度的变化趋势完全一致(图4),这表明粒子的定向运动和膜两侧的渗透压差别关系不大,其原因可能是胶体粒子浓度太小(Φ0=0.012),导致膜两侧渗透压差别也很小,不足以驱动粒子运动.

图4 纯水-滤膜-粒子溶液(WP)体系和溶液-滤膜-粒子溶液(PP)体系在不同时刻的粒子浓度分布Fig.4.Particle concentration profiles in water-film-particle(WP)system and particle-film-particle(PP)system at different times.

为了进一步分析粒子定向运动的原因,将滤膜浸泡在纯水溶液中,然后用离子色谱仪(DIONEX ICS2500,DIONEX ICS2000)测试了其中的离子成份,结果如表1 所列.从表1 可以看出,纯水中所有阴阳离子含量都很低,低于纯水自电离产生的H+和OH—的浓度(1.0×10—7mol/L),可以忽略不计.但是,在纯水中放入滤膜后,阴阳离子浓度显著增大,Cl—,,K+为10—6mol/L 量级,Na+为10—5mol/L 量级,分别是纯水情况下的10 倍和100 倍,这些离子的释放可能是导致粒子产生朝向滤膜运动的主要原因.

表1 滤膜中所含离子的成分、浓度以及相关离子的迁移率Table 1.Ion species and concentration contained in the film and the mobility of relevant ions.

对于粒子在阴阳离子存在条件下的运动,传统扩散泳理论给出了解释[19-22].一方面,如果溶液中存在扩散速率不同的阴阳离子,离子扩散将会导致电荷分离产生扩散电势,驱动溶液中的带电粒子发生定向的电泳运动(EP).从表1 离子迁移率可以看出,在浓度大于10—7mol/L 的几种离子中,阴离子Cl—的迁移率最大,Cl—的扩散将会形成一个从膜指向样品管远端的扩散电势,驱使带负电的胶体粒子朝向滤膜运动.另一方面,阴阳离子从膜扩散而来,在粒子朝向膜的一侧和背向膜的一侧形成电解质浓度的差异,在电解质浓度高的一侧,粒子表面双电层内流体的压力较大,使双电层内流体和粒子表面产生相对滑移,流体流向低浓度电解质一侧,而粒子被挤压朝向高电解质浓度一侧,称之为化学泳(CP).粒子的扩散泳速度可写为vpΓp∇lncs,式中cs是电解质溶液浓度;Γp是粒子的扩散泳迁移率,其中第1 项是粒子电泳的贡献(ΓEP),第2 项是粒子化学泳的贡献(ΓCP),ε和η分别是溶液的介电常数和黏度,kB是玻尔兹曼常数,T是热力学温度,z是电解质价数,e是电子电量,ζp是粒子zeta 电位值,β是反映电解质阴阳离子迁移率差异的常数.需要指出的是,对于本文中的混合电解质溶液[23,24],在不考虑低浓度离子(离子浓度小于10—7mol/L)的情况下,β可表示为:其中D+,i,xi分别是第i种阳离子的迁移率和摩尔分数,在这里包括Na+,,K+三种阳离子,Dcl-是Cl—的迁移率.

据此,可以建立粒子的运动方程.粒子迁移运动的通量j可以表示为:j-D∇cp+cpvp,D是粒子扩散系数,cp是粒子浓度.根据粒子数守恒∂cp/∂t+∇·j0,二维情况下的控制方程可以写为

首先,扩散泳只发生在盐浓度梯度∇lncs方向,即y方向(图5(a));其次,如果只考虑y方向的扩散(粒子扩散的主要起因是扩散泳导致的y方向的粒子浓度梯度,因此这么考虑是合理的),则(2)式可以简化为

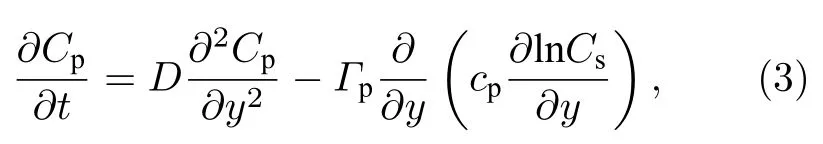
初始条件为cpc0(t0),边界条件为(x0,xW),0(y0,yL),其中W和L分别为样品管投影矩形的宽和长.对方程(3)进行数值求解,结果如图5(b)所示,可以看出计算结果和实验结果具有较好的一致性,说明模型比较准确地抓住了粒子运动的内在物理机制,即粒子扩散泳和扩散是粒子朝膜定向迁移的主要原因.需要指出的是,在模型中忽略了重力的作用(重力方向为+y方向,和粒子运动方向相反),因为文中所用胶体粒子直径较小,和水的密度差也仅为0.05 g/cm3,Peclet 数远小于1[25],重力影响很小.

图5 模型示意图(a)和数值计算结果(b)Fig.5.Schematic diagram of the model(a)and the numerical simulation results(b).

3.2 粒子横向运动

为了分析壁面区域粒子数的变化规律,根据图3(a)中的Φ-L曲线构建了一个简单模型(见图6(a)),用Φ-L曲线和Φ0之间的面积近似代表区域内的粒子数量N:

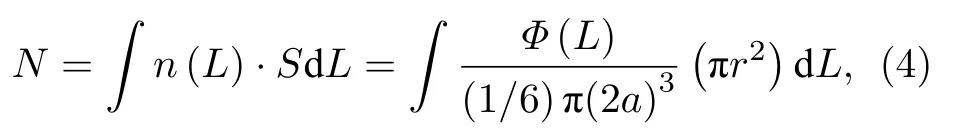
其中r和S分别是样品管内径和截面积,n(L)和Φ(L)分别是L处粒子的数密度和体积分数.根据(4)式,在一定时间内增加的粒子数N+、减少的粒子数N—以及净变化的粒子数Nnet分别为

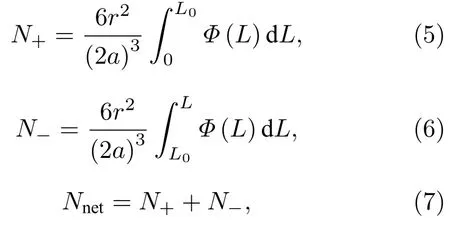
式中L0表示Φ-L曲线与Φ0的交点,Φ＞Φ0区域内粒子数增加,Φ<Φ0区域内粒子数减小,据此计算的粒子数目变化如图6(b)所示.

图6 壁面粒子数的计算(a)粒子迁移量计算示意图;(b)增加的粒子数、减少的粒子数和粒子数净变化Fig.6.Calculation of particle numbers near the container wall:(a)Model used to calculate the number of migrated particles;(b)the increased,decreased and the net change of particle numbers.

可以看出,在滤膜和胶体粒子溶液接触的前5 个小时,样品管上部增加的粒子数N+和样品管下部减少的粒子数N-基本是等量的,Nnet0,粒子数守恒.从t＞ 5 h 开始,N+继续增加,但是N-减小变缓,Nnet0且Nnet＞0 .这里有两点需要说明:第一,Nnet0 意味着粒子数不守恒.对比图3(a)的Φ-L曲线可以发现,粒子数不守恒的发生时刻恰好是样品池底部粒子数发生改变的时刻,即粒子扩散泳运动传导到池底的时刻.由于粒子扩散泳只发生在∇lncs方向(见图5),粒子朝向滤膜发生迁移之后,样品池底不能及时提供用以补充的粒子,所以发生了粒子数不守恒的现象.第二,Nnet＞0意味着粒子除了发生朝向滤膜的纵向迁移之外,还发生了朝向器壁的横向迁移.显然,仅仅考虑粒子扩散泳运动,无法对此进行解释,因为扩散泳只在纵向起作用.分析认为粒子横向迁移的原因大致有3 种.

1)粒子扩散.已有研究证实,在溶液中扩散电势的作用下,玻璃池壁表面会产生电渗流影响粒子的运动和组织行为[26,27].在本研究中,扩散电势方向指向池底,池壁表面电渗流vw也是朝向池底,与粒子扩散泳vp方向相反,因此壁面处粒子的运动速度为vp-vw,远离壁面处的粒子运动速度为vp,由于粒子运动速率的差异,就会在样品池的横向方向形成粒子浓度梯度,扩散效应导致粒子发生横向的迁移.

2)粒子升力.流场中的物体通常会受到垂直于主流方向的侧向升力,Segre 和Silberberg[28]于1961 年首次发现颗粒在圆管层流中的侧向迁移效应.理论研究表明Navier-Stokes 方程中的非线性惯性项是其主要原因,因此颗粒的这种侧向迁移也称之为惯性迁移效应[29].Rubinow 和Keller[30]进一步推导出了管道流中不同径向位置处颗粒受到的升力Fl∝a5R,其中a为粒子半径,R为粒子在管道中的径向位置.粒子扩散和粒子升力似乎解释了粒子朝向壁面发生横向迁移的原因,但是进一步的估算表明,无论是粒子扩散系数(D～10-12m2/s)相比较于粒子扩散泳系数(Γp～10-10m2/s),还是升力(Fl∝a5)相比较于Stokes阻力(假设平衡时扩散泳驱动力和Stokes 阻力相等,Fs∝a),都存在数个数量级的差异,因此单纯依靠扩散和粒子升力不足以导致粒子产生明显的横向迁移运动.

3)池内流动的影响.溶液中扩散电势的存在,使得样品池内沿着池壁产生从滤膜指向池底的电渗流vw,由于流体的不可压缩性,池内将会形成以样品池轴线为对称轴的左右两侧环流(图7),这种由于外场梯度(温度梯度、浓度梯度)导致的环流十分常见[31,32].在环流的作用下,样品池上部粒子被输送靠近壁面,下部粒子被输送远离壁面,由于上部粒子浓度cp_top比下部粒子浓度cp_bottom要大,就会导致朝向壁面的横向粒子净迁移vw×(cp_top-cp_bottom).但是,鉴于粒子运动受到多方面因素影响的复杂性,我们目前尚未建立起合适的粒子横向运动模型,此方面研究有待进一步的开展,特别是壁面流动的计算.

图7 样品池内流动示意图Fig.7.Schematic diagram of flow in the sample cell.

4 结论

本文用带电胶体粒子作为蛋白质等带电物质原型,分别研究了纯水-滤膜-带电粒子和带电粒子-滤膜-带电粒子两种不同体系中纤维素滤膜对带电微粒运动行为的影响规律.结果发现带电粒子会大量富集在滤膜附近,离子色谱分析表明纤维素滤膜在水中会释放少量的Na+,K+,Cl—等阴阳离子,这些离子扩散速率不同导致的粒子扩散泳效应是驱动粒子朝向滤膜运动的主要原因.基于粒子扩散泳和粒子扩散的物理机制,建立了粒子运动模型并进行了数值计算,计算结果和实验结果具有较好的一致性.此外,研究还发现粒子除了发生朝向滤膜的纵向迁移之外,还会发生朝向管壁的横向迁移,单纯考虑粒子扩散泳无法对此进行解释,必须考虑壁面渗流导致的池内环形流动对粒子输运的影响.本文的研究结果在认识滤膜和带电组分之间复杂相互作用机制,提高溶液中蛋白质等带电组分的回收率和减小滤膜污染等方面具有重要的参考意义.