兼顾地形形态与特征的非航海TIN-DDM自动综合算法

季宏超，董 箭，李树军，张志强，魏 源,3

1. 海军大连舰艇学院军事海洋与测绘系，辽宁 大连 116018； 2. 海图信息中心，天津 300450； 3. 91937部队，浙江 舟山 316002

数字水深模型(digital depth model，DDM)是利用有限、离散的水深点实现对海底地形表面高低起伏形态的数字化表达，根据水深点数据组织方式的不同，分为规则格网DDM(GRID-DDM)和不规则三角网DDM(TIN-DDM)[1-6,26]。相比于GRID-DDM，TIN-DDM未经过任何数据内插处理，且直接采用实测水深作为其模型采样点，因此TIN-DDM在反映地形形态变化方面的优势相对突出，基于TIN-DDM的海底地形形态分析结论相对更加准确[1-3,7]。随着海底观探测技术的发展，高分辨率、海量水深数据支持的高保真TIN-DDM构建、分析及表达在海底工程建设、海洋地学研究、水下武器装备效能评估等方面愈发受到重视[7]。

根据应用场景及对象的需求不同，TIN-DDM可被划分为航海TIN-DDM与非航海TIN-DDM。区别于强调舰船海上航行安全的航海TIN-DDM，非航海TIN-DDM的应用场景与陆地数字高程模型(digital elevation model，DEM)相一致，其应用对象的基本需求是在识别海底地形形态和维护海底地形特征的基础上，强调航行资源的有效利用，辅助海底工程建设、水下武器装备效能评估等方面的决策分析，同时为海洋地学等科学研究领域提供重要技术支持[1-3,7]。因此，非航海TIN-DDM的构建、分析及表达需重点关注采样点邻域构成的海底地形形态判定是否准确、反映海底地形特征的采样点保留是否充分，尤其在TIN-DDM综合的过程中，随着TIN-DDM采样点数量的压缩，利用有限采样点实现TIN-DDM地形特征的充分性维护是实现高保真TIN-DDM多尺度表达的关键环节。

受传统航海TIN-DDM主要服务于舰船航行安全保障的固定思维约束，目前专门针对非航海TIN-DDM应用需求的自动综合算法研究较少[7]。而由于非航海TIN-DDM与陆地DEM应用场景的相似性，现有的非航海TIN-DDM自动综合算法多数通过借鉴和改进陆地TIN-DEM多尺度表达算法获得，如信息量判别法、三角面片法、矢量夹角法、点面距法、三维Douglas-Peucker法等[8-11]。尽管海底地形特征与陆地地形特征在几何特性上并无差异，均由地形特征点、线共同构成，但与陆地TIN-DEM在数据采集时已包含完整的地形控制信息(一般由典型的地形特征点构成)不同，海底地形测量由于其测量手段和方式的特殊性，无法直接获得海底地形特征信息及与之相关的海底地形范围。因此，现有的自动综合算法难以实现非航海TIN-DDM中深层次地形特征信息的充分挖掘，且针对空间尺度与地形形态判定结论的关联性探索不够深入。自2003年Smith提出了面向航海表面(navigation surface，NS)服务的滚动球变换概念，滚动球变换严密的几何特征度量特性被广泛应用于DDM构建及多尺度表达中[12-17]。文献[7]结合非航海TIN-DDM的应用需求，提出了顾及地形形态多尺度表达的TIN-DDM快速自动综合算法，该算法利用滚动球变换的地形形态定量识别特性，构建了采样点地形类型与滚动球半径的关联模型，通过对滚动球接触点与滚动球半径的数值关联性分析，实现了面向非航海TIN-DDM地形形态连续尺度表达的滚动球变换[12]。

文献[7]将采样点地形类型与滚动球半径的关联模型应用于非航海TIN-DDM地形形态连续多尺度表达过程，在一定程度上解决了陆地TIN-DEM多尺度表达算法在非航海TIN-DDM综合应用中存在的地形形态划分边界不明确、空间尺度认知存在差异等问题。然而，文献[7]中采样点地形类型与滚动球半径的关联模型，仅实现了依据临界滚动球半径数值的TIN-DDM采样点地形类型判定，既无法定量描述采样点地形类型的区域边界(范围)，更难以反映采样点地形类型由微观至宏观的连续形态变化规律，由此导致了TIN-DDM综合结论的相对不确定性。此外，文献[7]提出了删除平坦(起伏程度较小)地形采样点和保留复杂(起伏程度较大)地形采样点的非航海TIN-DDM综合思路，在一定程度上尽管实现了TIN-DDM整体地形的形态维护，但由于缺乏平坦地形采样点的概念界定及其在复杂地形形态中的特征值量化评价，难以实现海底地形形态识别的准确性及整体海底地形特征维护的充分性。

为解决上述问题，本文在深入分析文献[7]算法的基础上，将地形形态识别范围的概念引入TIN-DDM采样点地形类型与滚动球半径的关联模型，以临界滚动球半径为关联纽带，建立了面向宏观、微观地形的采样点地形类型精细化判定流程，通过连续尺度变换条件下采样点临界滚动球半径的数值变化规律分析，设计了面向海底地形形态识别的采样点地形特征定量评价指标，构建了依采样点评价指标的TIN-DDM自动综合算法，实现了兼顾地形形态与特征的非航海TIN-DDM自动综合。

1 顾及地形形态多尺度表达的TIN-DDM快速自动综合算法及局限性分析

1.1 算法基本原理

为便于算法叙述，首先引入滚动球变换的概念。参照文献[14]，滚动球变换定义为三维空间一无限光滑球体沿TIN-DDM一侧滚动并生成轨迹曲面的一种几何变换。滚动球变换有正向和负向之分。数学形式上，滚动球变换等价于TIN-DDM正向缓冲体边界变换与负向缓冲体边界变换的组合。图1为TIN-DDM滚动球变换的纵向剖面图。图1中，r表示滚动球半径；黑色实线表示TIN-DDM地形纵向剖面；黑色虚线表示滚动球球心位于TIN-DDM表面滚动形成的上下缓冲体边界；滚动球沿TIN-DDM上下表面滚动(球心位于TIN-DDM上下缓冲体边界)将形成新的上下轨迹曲面。

图1 滚动球变换原理Fig.1 The principle of rolling ball transformation

文献[12]在分析滚动球上下轨迹曲面形态差异的基础上，通过分析滚动球接触点与滚动球半径之间的数值关联，顺次求解各TIN-DDM采样点与滚动球接触状态变化时的临界滚动球半径，构建了TIN-DDM采样点地形类型与滚动球半径的关联模型。即

(1)

文献[7]利用式(1)设计了与地形形态连续尺度表达过程相一致的TIN-DDM自动综合算法。为控制综合后的TIN-DDM精度，文献[7]算法利用2倍的测量中误差(2Δδ)作为特征地形识别和平坦地形高程的传递阈值，通过设定两种综合判据的方式，对经计算小于此阈值的采样点进行删除。第1种综合判据(简称“判据1”)是将被判别采样点与其最近采样点的深度差值Δh与2Δδ做比较；第2种综合判据(简称“判据2”)是将凹(凸)性地形采样点的凹(凸)程度Δd与2Δδ做比较。

1.2 算法局限性分析

尽管文献[7]算法在一定程度上实现了TIN-DDM整体地形的形态维护，但该算法无法定量描述TIN-DDM采样点地形类型的区域范围，且缺乏平坦地形采样点的概念界定，难以保证海底地形形态识别的准确性及整体海底地形特征维护的充分性。

1.2.1 海底地形形态识别准确性方面

由海底地形连续可微的特性可知，海底地形形态的识别效果与其所处的区域分布范围密切相关。如图2(a)所示，A、B、C、…、J为TIN-DDM上相邻的采样点(以黑色圆点表示)，采样点顺次连接形成的黑色实线表示TIN-DDM的地形纵向剖面。其中，A、E、F、J的水深值相同，且A、E间的距离与F、J间的距离相等；B、D、G、I浅于A、E、F、J，同样具有相同水深值，且B、D间的距离与G、I间的距离相等；C位于B、D的垂直平分线上，且水深值介于A、B之间；H位于D、I的垂直平分线上，且水深值介于F、J之间；C浅于H。基于上述假设，C、H在TIN-DDM地形纵向剖面中均为凹性地形采样点，且TIN-DDM采样点H所表达的凹性地形的程度强于采样点C。由于采样点所表达的地形凹凸程度由弱到强的变化过程与TIN-DDM地形形态综合尺度由小到大的变化过程相一致，故在TIN-DDM综合过程中采样点C应优先于采样点H被删除。

图2 海底地形形态识别准确性分析Fig.2 The analysis of seabed topographic forms recognition accuracy

基于上述分析可知，由于该模型无法定量描述凹性地形和凸性地形的区域分布范围，导致其地形类型的判定结论存在一定的不确定性，最终造成了其采样点综合点序与地形形态综合尺度变换的不一致性。

1.2.2 海底地形特征维护充分性方面

地形特征是地形形态征象的概括和抽象，通常以地形特征点、线的方式组织和表达，但由于地形综合的多尺度特性，地形特征本质上是地形采样点的固有属性。如图3(a)所示，A、B、C、…、I为TIN-DDM上相邻的采样点(以黑色圆点表示)，采样点顺次连接形成的黑色实线表示TIN-DDM的地形纵向剖面。其中，C位于在地形起伏较大区域(以红色虚线框标记)的坡面上，其至相邻采样点连线的距离为hC；F、G、H位于地形起伏较小的平坦区域(以绿色虚线框标记)，其至各自相邻采样点连线的距离分别为hF、hG、hH，且hF=hG=hH>hC。根据文献[7]算法的综合思路，因采样点F、G、H处于地形起伏较小的区域内，在综合过程将作为“平坦地形采样点”被优先删除。然而，需要指出的是：一方面，尽管采样点C所处区域的地形起伏较大(地形较复杂)，但由于采样点C与B、D近似共线(hC数值较小)，采样点C的删除对其所处区域的地形起伏影响不大(即采样点C的地形特征表达能力较弱)，故采样点C应同样作为“平坦地形采样点”被优先删除；另一方面，尽管采样点F、G、H所处区域的地形起伏较小(地形较平坦)，但其在该区域的地形特征表达作用相对明显(直接决定了该区域的平坦程度)，且由于hF=hG=hH>hC，故采样点F、G、H的地形特征表达能力应强于采样点C。由于采样点表达地形特征的能力由弱到强的排列顺序与地形形态综合尺度由小到大的变化过程相一致，故采样点C应先于采样点F、G、H被删除。

分别计算采样点H与其最近采样点I的深度差ΔhI与采样点C、F、G的凹凸程度ΔdC、ΔdF、ΔdG(如图3(b)所示)。由于采样点C、F、G的凹凸程度与采样点H深度差之间存在ΔdG<ΔdF<ΔhI<ΔdC的数值大小关系，如若依据“判据2”的删点原则，采样点F、G、H应先于采样点C被删除，这与图3(a)中“采样点C应先于采样点F、G、H被删除”的分析结论不符。

图3 海底地形特征维护充分性分析Fig.3 The analysis of seabed terrain features maintenance adequacy

基于上述分析，文献[7]算法针对“平坦地形采样点”的概念相对狭义，且无法实现采样点地形特征表达能力的定量描述，部分复杂地形中的“相对平坦采样点”无法有效删除，最终难以保证TIN-DDM整体地形特征维护的有效性。

2 面向采样点地形特征定量评价的TIN-DDM自动综合模型

作为非航海TIN-DDM自动综合的基础前提，海底地形形态识别的关键在于凹凸地形识别范围的准确界定，考虑到TIN-DDM任意采样点Pi处的局部地形形态分布取决于其Delaunay影响域的位置与范围，本文将Delaunay影响域引入海底地形形态的识别过程，结合滚动球在TIN-DDM表面滚动过程中与采样点接触程度的变化规律分析，建立微观至宏观的采样点地形类型精细化判定模型，实现采样点地形类型的识别。

2.1 TIN-DDM采样点微观地形类型与滚动球半径的关联模型

Delaunay影响域是指包含采样点Pi的Delaunay三角形组成的空间邻域，其在几何上定义了距离采样点Pi的最近采样点集，即为包含采样点Pi的Voronoi单胞V(S,Pi)与其相邻Voronoi单胞共同所对应采样点组成的区域[18-19]。即

H(S,Pi)={Pj|G(S,Pi,Pj)≠Ø}

(2)

式中，H(S,Pi)表示S中采样点Pi的Delaunay影响域；采样点Pj表示H(S,Pi)的任意顶点；G(S,Pi,Pj)表示采样点Pi的任意Voronoi边。如图4所示，采样点Pi周围的阴影部分即为其Delaunay影响域H(S,Pi)[18]。

图4 Delaunay影响域概念Fig.4 The concept of Delaunay influence domain

由当前测深系统中海底地形跟踪与控制相关原理可知，在地形任意方向上至少存在连续记录的3～5个采样点才可判定海底凹凸地形的存在。Delaunay影响域位置与范围的唯一性及其所关联采样点数量在地形形态识别方面的有效性，决定了Delaunay影响域可作为海底微观地形类型判定的区域分布范围[20-21]。由于Delaunay三角形的空外接圆特性，Delaunay影响域内的采样点与外部采样点相对独立。因此，Delaunay影响域约束下的采样点地形类型与滚动球半径关联模型在地形类型判定的结论上将会出现明显改变。式(1)改化为

(3)

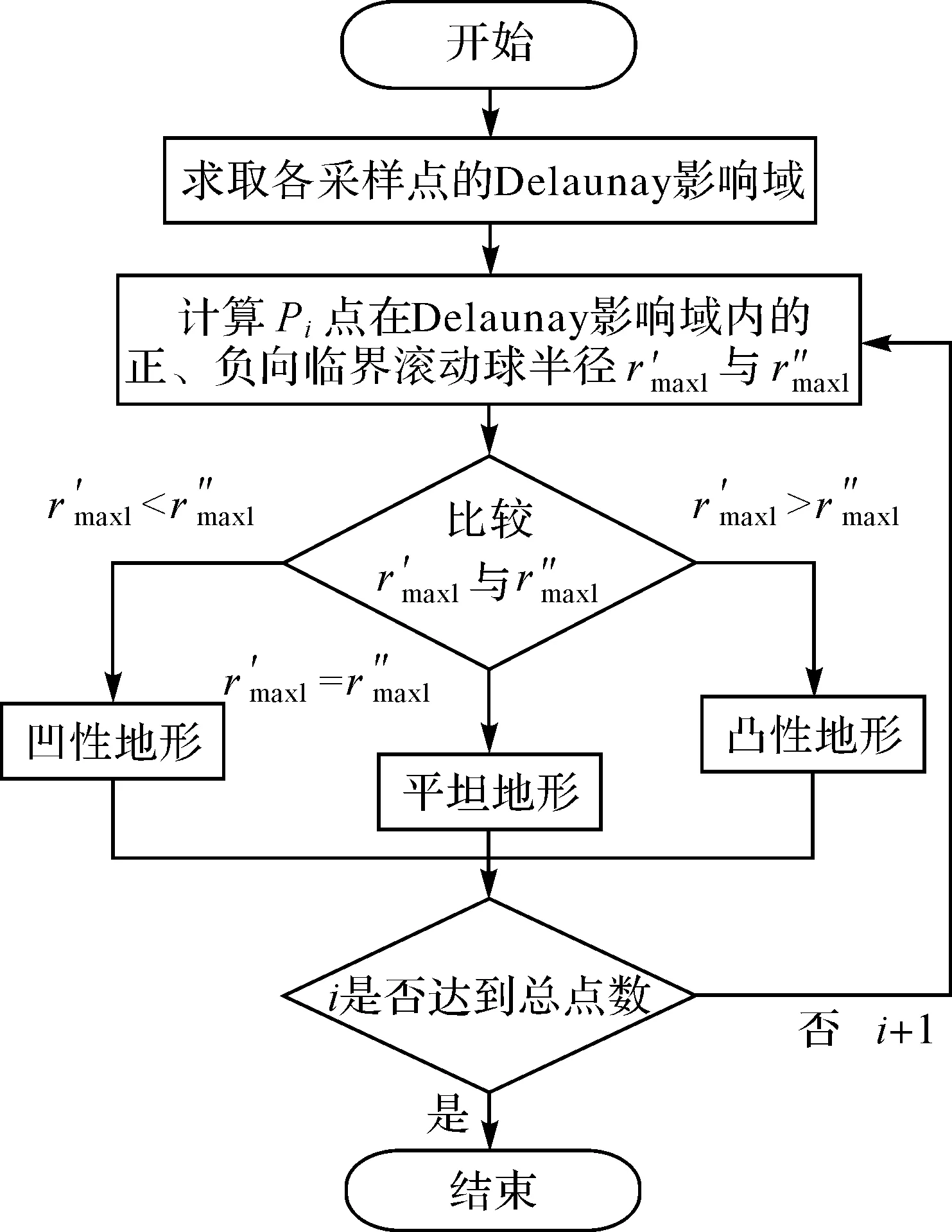
图5 采样点微观地形类型判定流程Fig.5 Determination process for the micro-topography type of sampling point

2.2 TIN-DDM采样点宏观地形类型与临界滚动球半径关联模型

在Delaunay影响域约束的微观地形类型判定的基础上，进一步考虑地形结构信息对TIN-DDM综合的影响，本文依据临界滚动球半径数值变化规律对采样点进行了宏观尺度上的地形类型划分。如图6所示，A、B、C、D、E为TIN-DDM上相邻的采样点(以黑色圆点表示)，采样点顺次连接形成的黑色实线表示TIN-DDM的地形纵向剖面。其中，A、E深度值相同；B、D浅于A、E，同样具有相同水深值，且B、D与A、E的垂直平分线相互重合；C位于B、D的垂直平分线上，浅于B、D。

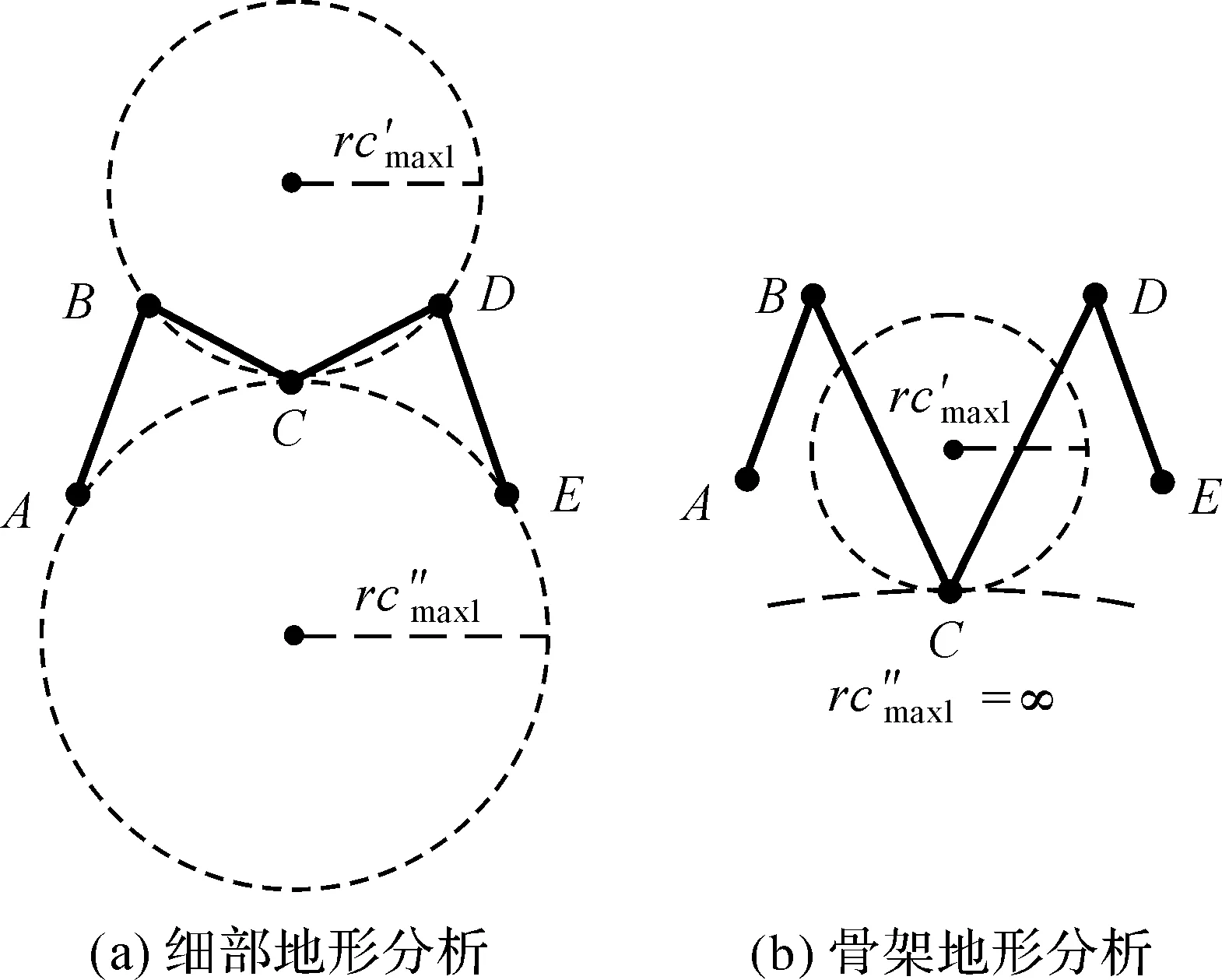
图6 采样点宏观地形类型与临界滚动球半径关联性分析Fig.6 Correlation analysis between macro-topography type and critical rolling ball radius of sampling points

(4)

式中，QH(Pi)表示TIN-DDM采样点Pi的宏观地形类型属性；1为细部地形；2为凸性骨架地形；-2为凹性骨架地形。

2.3 面向海底地形形态识别的TIN-DDM采样点地形特征定量评价指标

在采样点地形类型识别的基础上，定量分析和评价采样点的地形特征表达能力，实现地形形态识别条件下采样点综合点序的严密生成，是实现海底地形特征充分性维护的基础前提。为此，本文通过连续尺度变换条件下采样点临界滚动球半径的数值变化规律分析，阐明了采样点地形特征表达能力与正负向临界滚动球半径比值相关性，设计了面向海底地形形态识别的TIN-DDM采样点地形特征定量评价指标。如表1所示，TIN-DDM上相邻的采样点(以黑色圆点表示)顺次连接形成的黑色实线表示TIN-DDM的地形纵向剖面；采样点A、B所在地形均为凹性细部地形；采样点C、D所在地形均为凸性细部地形；采样点A、B、C、D在纵向上连续变化，其余采样点位置恒定。

表1 临界滚动球半径与细部地形采样点地形特征表达能力关联性分析Tab.1 Correlation analysis between critical rolling ball radius and terrain feature expression ability of detail topography sampling points

(5)

表2 临界滚动球半径与骨架地形采样点地形特征表达能力关联性分析Tab.2 Correlation analysis between critical rolling ball radius and terrain feature expression ability of skeleton topography sampling points

(6)

式中，Ωskeleton(Pi)表示骨架地形采样点Pi的地形特征评价指标。由于细部地形采样点地形特征评价指标Ωdetail(Pi)的取值区间在0至+∞之间，而骨架地形采样点地形特征评价指标Ωskeleton(Pi)的取值区间同样在0至+∞之间，在数值上无法有效区分细部地形采样点与骨架地形采样点，由此本文通过对采样点地形特征评价指标进行公式变换的方式，实现细部(骨架)地形采样点地形特征评价指标在数值上的有效区分。即

(7)

图7 平坦地形采样点地形特征评价指标分析Fig.7 Evaluation index analysis of terrain feature for flat topography sampling points

2.4 TIN-DDM采样点综合点序分析

为维护TIN-DDM整体地形特征的充分性，同时兼顾采样点综合数量的要求，在非航海TIN-DDM自动综合中，地形特征表达能力较弱(较强)的采样点应优先删除(保留)。由此，地形特征表达能力较弱，即地形特征评价指标数值较小的采样点，应被视为TIN-DDM自动综合过程中优先删除的采样点。如图8所示，依地形特征评价指标数值的采样点综合点序与地形形态综合尺度变换的过程一致。

图8 采样点综合点序分析Fig.8 Generalization point sequence analysis of sampling points

3 试验与分析

为验证本文所提算法在TIN-DDM地形特征维护方面的充分性，本文在C#环境下实现了本文算法和文献[7]算法，并利用Surfer与Matlab软件对试验结果进行可视化显示与分析。试验数据为我国某海区的多波束水深数据构建的TIN-DDM，共包含12 774个采样点且已经过误差改正、粗差剔除等前期处理。试验环境为Inter(R)core(TM)i5处理器，主频为2.5 GHz，内存为8 GB。图9为原始TIN-DDM的地形表面。

图9 原始TIN-DDM地形表面Fig.9 Original TIN-DDM topographic surface map

利用本文算法和文献[7]算法分别对原始TIN-DDM进行综合处理，综合过程中删除的采样点数量分别为2000、4000、6000、8000、10 000。图10、图11分别为不同数量采样点删除后的TIN-DDM地形表面图及二维投影图，A区域为海底沟壑构成的面状区域(简称“面状沟壑区域”，以红色实线表示)；B区域为海底沟壑构成的条带状区域(简称“条带状沟壑区域”，以绿色实线表示)。

图10 不同数量采样点删除后的TIN-DDM地形表面图Fig.10 TIN-DDM topographic surface map after deletion for different number of sampling points

图11 不同数量采样点删除后的TIN-DDM二维投影图Fig.11 TIN-DDM two-dimensional projection after deletion for different number of sampling points

试验结果表明：①在综合尺度较小的情况下(采样点删除数量分别为2000、4000、6000时)，由于两类算法中均采用了平坦地形采样点优先删除、复杂地形采样点首要保留的TIN-DDM综合思路，两类算法的综合效果基本相同；②随着综合尺度的增大(采样点删除数量分别为8000、10 000时)，由于两类算法在“平坦地形采样点”概念界定上的不同，尽管在A区域的综合效果区分不大，但在B区域呈现出本文算法效果优于文献[7]算法的趋势。主要原因在于：相比于B区域，A区域中的海底沟壑分布较广且相对集中，文献[7]算法将此区域中的采样点多数判定为“复杂地形采样点”，采取优先删除B区域中“平坦地形采样点”的策略保证A区域的地形特征，导致难以维护B区域的地形特征；本文算法的微观、宏观地形类型判定原理实现了复杂地形中部分“相对平坦采样点”的有效识别，且利用地形特征评价指标对各类“平坦地形采样点”进行了综合点序的严密生成，在充分维护A区域面状海底沟壑特征的基础上，保证了B区域条带状海底沟壑特征的有效保持。

其次，为验证本文算法在TIN-DDM地形形态识别方面的优势，将文献[7]算法中采样点地形类型与滚动球半径关联模型(式(1))与本文算法的采样点地形特征定量评价指标(式(5))相结合形成对比算法。利用本文算法和对比算法分别对原始TIN-DDM进行综合处理，综合过程中删除的采样点数量分别为2000、4000、6000、8000、10 000。图12为不同数量采样点删除后的TIN-DDM地形表面。

图12 算法地形形态识别分析Fig.12 Analysis of algorithm for topographic form recognition

试验结果表明：①在综合尺度较小的情况下(采样点删除数量分别为2000、4000、6000时)，由于两类算法利用滚动球半径数值比较确定采样点地形类型的总体思路不变，两类算法的综合效果基本相同；②随着综合尺度的增大(采样点删除数量分别为8000、10 000时)，在C区域(以红色矩形区域表示)呈现出本文算法效果优于对比算法的趋势。主要原因在于：相比于本文算法，对比算法中的采样点地形类型的区域分布范围不明确，其在地形类型的判定结论方面存在一定的不准确性，进而影响地形特征评价指标数值的准确计算和综合点序的严密生成，由此导致C区域中原本连续分布的海底沟壑经对比算法综合后呈现出不连续性加剧的趋势。

然后，为验证本文算法在TIN-DDM精度保持方面的优势，将经本文算法和文献[7]算法综合后的TIN-DDM分别与原始TIN-DDM进行叠置分析，计算综合前后TIN-DDM的地形表面积差、包含水体体积差(由TIN-DDM地形表面至0 m水深平面所包含的水体体积)。如图13所示，本文算法在TIN-DDM地形表面积差、包含水体体积差方面的数值均明显小于文献[7]算法，即本文算法具有较高的算法精度。

图13 算法精度分析Fig.13 Algorithm accuracy analysis

最后，为验证本文算法在地形特征维护方面的优势，利用ArcGIS 10.1中的地形特征线提取功能(基于地表流水模拟法[22-26])提取原始TIN-DDM栅格化后的地形特征线，并依据提取的地形特征线对原始TIN-DDM中采样点进行邻近度分析，提取原始TIN-DDM中的地形特征点(总数为2229。山谷点数为916；山脊点数为1313)，依据地形特征点对经本文算法和文献[7]算法综合后的TIN-DDM采样点进行比对与分析。如图14所示，相比于文献[7]算法，本文算法综合后的TIN-DDM采样点中包含更多的地形特征点，即具有较好的地形特征维护优势。

图14 算法地形特征维护分析Fig.14 Analysis of algorithm for terrain feature maintenance

4 结 论

本文从海底地形形态识别和海底地形特征维护的应用需求出发，提出了面向非航海TIN-DDM地形形态连续尺度表达的滚动球变换综合算法的改进思路。以采样点地形类型的有效识别为目标，将Delaunay影响域引入海底地形形态的识别过程，结合滚动球在TIN-DDM表面滚动过程中与采样点接触程度的变化规律分析，建立了微观至宏观的采样点地形类型精细化判定模型；以定量分析和评价采样点的地形特征表达能力为要求，通过连续尺度变换条件下采样点临界滚动球半径的数值变化规律分析，阐明了采样点地形特征表达能力与正负向临界滚动球半径比值相关性，设计了面向海底地形形态识别的TIN-DDM采样点地形特征定量评价指标，建立了依地形形态综合尺度变换的采样点综合点序。试验分析表明：本文算法能在识别海底地形形态的基础上实现海底地形特征的有效维护，且具有较高的TIN-DDM精度保持优势。由于算法在数据预处理阶段未对TIN-DDM建立分块索引，难以实现算法的并行处理，算法整体耗时相对较大，下一步将研究滚动球变换过程中TIN-DDM的自适应分块及算法并行设计，实现算法运行效率的显著提升。