序列卷积神经网络支持下线状地图目标的分段方法

2023-02-18李连营黄浩然晏雄锋

测绘学报 2023年1期

杨敏，陈果，李连营，黄浩然，苗静，晏雄锋,2

1. 武汉大学资源与环境科学学院，湖北武汉 430079； 2. 同济大学测绘与地理信息学院，上海 200092； 3. 武汉市测绘研究院，湖北武汉 430022

地图上的线状目标表示道路、河流、海岸线、行政区界线等地理实体。它们在几何形态上呈现不同的模式结构，反映所表达对象的空间分布特征和地理意义。特别地，同一线状目标的不同部分通常呈现出不同的模式类型。例如，经过不同性质滩涂的海岸线、表达不同类型地貌的等高线、穿越不同地形区域的道路线等。因此，对线状目标隐含的模式特征进行识别并实施分段处理具有重要意义[1]。以线状目标的制图综合为例，不同形态结构的曲线段需要采用不同的化简操作，从而保证输出结果的合理性[2]。前期研究工作主要关注综合变换操作的程序实现，针对线状目标设计了多种化简算法[3-6]。然而，如何合理地选择算法及参数，仍然依赖专业人员对线状目标模式特征的判断，导致综合实施过程的自动化水平不高[7]。因此，当前研究的重点逐渐转向线状目标的模式识别与分段工作[8]，以便不同模式的曲线段自动匹配相适应的化简算法，从而构建完整的“模式诊断→行为决策→操作执行”技术链条。

线状目标分段研究涉及两个方面：模式类型的划分和模式识别与分段方法的构建。前者属于空间认知范畴，要综合考虑线状目标的几何特征和地理属性。文献[9]将山区道路曲线段的模式划分为光滑、弯曲且方向固定、弯曲且方向不固定及非常弯曲。文献[10]将局部海岸线区分为光滑曲折性小、曲折但方向固定、弯曲且方向不明3种模式。本文关注后一阶段工作，即自动识别不同模式类型的曲线段并完成线状目标的分段处理。

针对这一问题，目前主要存在两类方法。

方法1：将某些特征点作为分段的切割位置，关注线状目标几何形态在特征点处延展方向的变化。特征点可以采用局部曲率极值点、拐点，也可以是通过曲线压缩方法对线状目标实施处理后保留的节点，如Douglas-Peucker(DP)算法[11]、Visvalingam-Whyatt(VW)算法[12]。该类方法采用节点间长度、角度、曲率等简单参量进行分析，对复杂形态结构的描述能力不足，难以保证按同质性原则输出曲线段。

方法2：将弯曲结构作为曲线形态的基本单元，通过对局部弯曲特征的统计分析实现不同模式曲线段识别。文献[13]利用移动窗口按固定步长沿着线状目标移动，统计每个窗口内曲线段的弯曲特征参量并结合神经网络技术进行形态结构的分类，最后将相邻窗口同种模式的曲线段合并实现分段输出。文献[10]利用同样的策略结合贝叶斯模型设计了海岸线的分段方法。相比较方法1，基于弯曲特征分析的方法能够更好地考虑高层次的形态结构，从而提升分段结果的合理性。然而，该类方法依赖人工选择特征参量，容易受到人的主观性影响。此外，不同要素类型甚至不同区域环境下分布的线状目标，需要选择不同的特征参量组合，导致实际应用难以推广。

针对现有方法的不足，本文引入卷积神经网络(convolutional neural network,CNN)构建线状目标的模式识别与分段方法。作为深度学习中的代表性算法，CNN仿造生物视知觉机制构建得到。通过隐含层内的卷积核参数共享和层间连接的稀疏性，CNN具备从浅层信息中提取深层次特征的能力[14]。早期CNN主要处理格点化或序列化特征数据，在图像分割[15-16]、自然语言处理[17]等任务中表现出色。通过重新设计卷积和池化等运算后，可拓展处理图结构组织的数据[18]。近些年，相关学者也将CNN及变种应用到地图数据处理中，包括面状目标形状编码认知[19]、岛屿边界线综合[20]，建筑物目标模式分类[21]、居民地综合处理[22-23]等。深度学习网络能够从样本数据中获取决策知识，无须人工进行特征选择与规则设计。从视觉认知的角度看，曲线的模式分段与图像的语义分割存在相似之处，即将具备相似特征的基本单元组合形成局部连续的同质结构。受此启发，本文提出如下的线状目标分段思路：将相邻节点构成的线元类比栅格模型中的像元，线状目标则组织为由线元描述特征构成的序列结构；在此基础上，将线状目标分段问题转化为每个线元的模式分类问题，并参考用于像元分类的全连接网络模型，构建序列卷积神经网络(sequential CNN,SCNN)用于线元特征序列学习与模式预测；最后，通过相邻且同种模式类型线元的合并处理输出分段结果。

1 方法

本文提出的线状目标分段方法包括3个步骤(图1)：①线元特征准备；②线元特征学习与模式分类；③分段结果组织与后处理。

图1 基于SCNN的线状目标分段模型框架Fig.1 Framework for segmentation of linear map objects using a SCNN model

1.1 线元特征准备

1.1.1 几何坐标预处理

图2 线状目标的几何坐标预处理过程Fig.2 The preprocessing of geometric coordinates of linear objects

(1)

1.1.2 线元特征提取与表达

假定预处理后线状目标L包含节点p1，p2，…，pn+1，pi=(xi,yi)(1≤i≤n+1)，其中，xi和yi表示pi的位置坐标，pi和pi+1所构成的直线段称为线元ei，如图3所示。线元作为线状目标的基本构成单元，其两侧端点的坐标差异体现了局部曲线段在该位置的微观变化，因此，本文以pi和pi+1间横坐标差Δxi和纵坐标差Δyi作为ei的描述特征，表示为(Δxi,Δyi)。那么，线状目标L的几何信息可表达为一系列线元特征构成的二维序列((Δx1,Δy1),(Δx2,Δy2),…,(Δxn,Δyn))，并以此作为模型的输入。

图3 线元特征的提取与表达Fig.3 Feature extraction and encoding for segment elements

1.1.3 线元模式类别标注

线元模式类别标注过程如图4所示。首先，由专业人员对线状目标进行分段，并标注出每条子线段的模式类别。模式类别的划分需要综合考虑地图比例尺、几何形态特点、后续应用需求等。然后，将每一子线段的模式类别信息赋予其包含的所有线元。最终，线状目标L的标注信息表达为标签序列T=〈t1,t2,…,tn〉，其中ti表示线元ei的模式类别。

图4 线元标注过程Fig.4 Illustration of the labeling for segment elements

1.2 线元特征学习与模式分类

本文参考经典U-net[15,17]构建面向序列数据的CNN模型进行线元模式特征分类识别。基本思想是通过多个卷积、池化、上采样运算单元将N×F维的输入特征，即1.1.2节中介绍的n×2维序列，变为一个同尺寸但更低维的向量(即N×1维)，即1.1.3节中介绍的n×1维标签。训练学习的目标是让输出向量与线元模式标注结果尽可能接近。整体网络架构如图5所示。

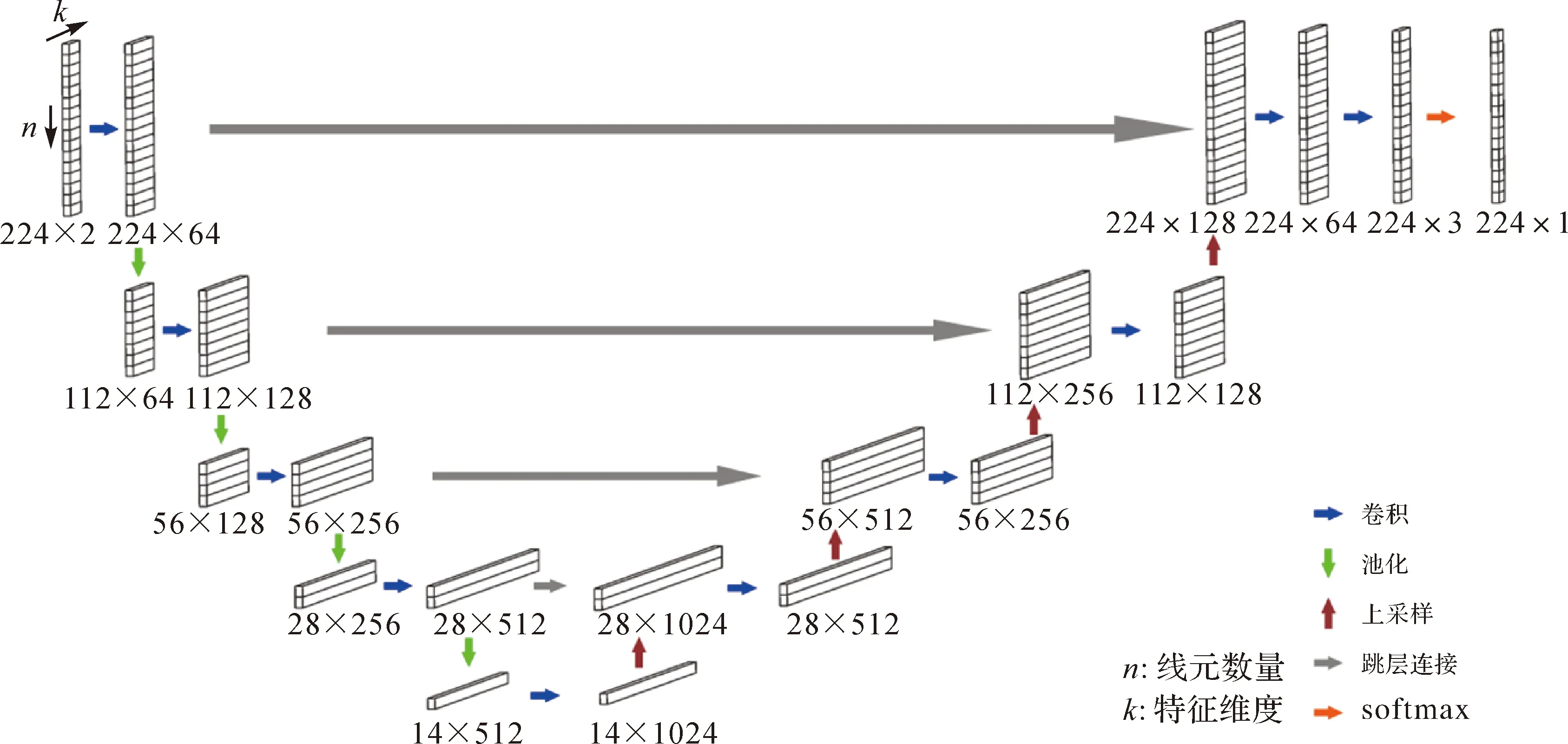
图5 面向线元模式分类的SCNN架构Fig.5 SCNN architecture for pattern classification of segment elements

1.2.1 卷积与池化运算

卷积运算的目的是从浅层次的线元特征中提取用于形态分析的高层次特征。先通过卷积滤波器对输入特征实施卷积运算，然后利用激活函数输出为卷积特征。由于线元序列属于一维结构，利用宽度为h的卷积核w∈hk对线元片段Li:i+h-1进行计算，产生新特征ci的表达式为

ci=f(w⊗Li:i+h-1+b)

(2)

池化运算通过间隔采样获取粗粒度的主体特征，有助于减少参数和计算量及防止过拟合现象，提升模型的泛化能力。本文采用最大池化运算，对窗口大小为l的线元片段特征Ci·s:i·s+l-1，取其最大特征值作为输出，表达式为

(3)

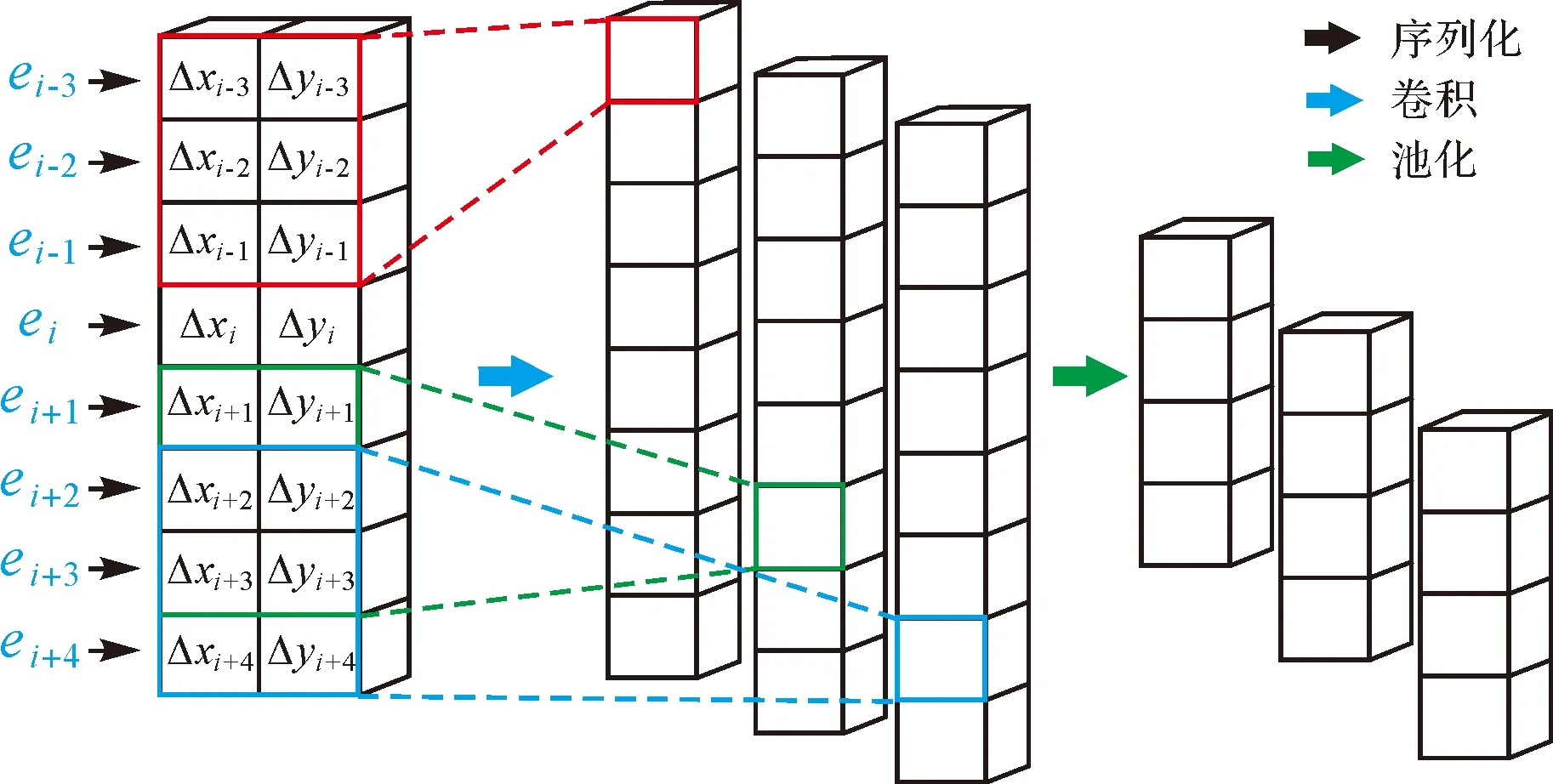
图6 序列数据的卷积和池化运算Fig.6 Convolution and pooling operations on sequential data

1.2.2 上采样运算与跳层连接

通过运用连续的上采样运算，特征图尺寸可恢复为原始输入大小。针对输入的特征图P，步长为s、卷积核尺寸为k的上采样运算表示为

U=WTP

(4)

式中，W表示卷积核的稀疏矩阵；U={u1,u2,…us(i-1)+k}为输出特征向量。

值得注意的是，池化及上采样运算会导致特征图中元素表达信息的损失。为了控制这种信息损失，建立特征提取阶段特征图与上采样阶段特征图间的跳层连接关系(图5)。具体地，将上采样后的特征图与特征提取阶段中与之通道数量相同的特征图进行拼接，从而产生一个通道数翻倍的特征图，然后运用卷积运算校正特征图中各元素的值使得通道数恢复。

1.2.3 分类预测与训练

在最后一层卷积运算后，得到长度为线元数量n、通道数为模式类别数量m的输出值。对于第i个线元(1≤i≤n)，其每个通道上输出值为zj(1≤j≤m)，用Softmax激活函数处理，即

(5)

模型训练过程表现为不断调整参数以最小化预测值与标签值之间的差异，即损失值。本文采用交叉熵作为损失值的度量函数，表达式为

(6)

式中，xi为第i个线元的预测值；yi为标签值。交叉熵越小，则预测值与标签值越接近。数据输入模型后先通过前向传播得到预测值，并计算其损失值；随后计算损失值相对各个参量的偏导数，并利用反向传播定理按给定学习率对参量进行更新，以逐步降低预测值与标签值之间的损失。

1.3 分段结果组织与后处理

将待分段的线状目标输入训练好的SCNN模型后，模型预测得到每个线元的模式类别；将相邻且模式类别相同的线元合并后形成曲线段，作为输出的分段结果。但初始分段结果中可能存在长度较短的曲线段(图7)，这不符合形态认知的连贯性原则。因此，本文采用一种迭代融合的方法用于分段结果后处理。首先，搜索长度最小且小于设定阈值lmin的曲线段，记为si，前后相邻曲线段为si-1、si+1；将si的模式类别调整为与si-1和si+1中较长者相一致并实施合并；重复上述步骤，直至所有曲线段长度大于阈值lmin。其中，lmin的取值由表达比例尺、后续应用需求等因素综合确定。

图7 分段结果的融合后处理Fig.7 Fusion processing of the segmentation results

2 试验分析与讨论

2.1 试验数据与模式类别划分

本文采用1∶5万行政区界线(广东省广州市)和1∶25万山区道路(四川省攀枝花市)开展试验。其中，行政区界线训练集和测试集包含线状目标数量分别为96和66，道路训练集和测试集的目标数量分别为81和27。几何坐标预处理时，行政区界线和道路目标的节点压缩矢高ε与内插距离阈值w分别设置为10、150和20、300 m。

对于行政区界线，结合本文试验数据的曲线形态特征以及不同综合化简算法处理数据的特点，划分为光滑型、折线型和弯曲型3种模式，如图8(a)所示。其中，折线型曲线段在一定范围内呈平直状，在某些位置切线方向发生变化而产生弯折，并且弯折处呈近似直角。该类型曲线段大多出现在居民地区域，综合化简时注重关键转折点的保留及正交特征的保持[5-6]。弯曲型曲线段的切线方向呈不规律变化，存在不同大小弯曲构成的复杂层次结构。该类型行政界线多源自复杂地形特征线，如山脊、海岸线等，需采用具备识别弯曲结构能力的化简算法[3]。光滑型线段的线形较为流畅，弯曲长度和半径较大，切线方向变化较为平缓。对于山区道路目标，参考文献[9]中考虑的方向变化、曲折度、光滑性特征，以及结合本文试验数据中常出现的曲线形态特征，最终划分为4种模式类别，分别是：①光滑型，线形流畅、曲折性小；②弯曲且方向固定型，存在小弯曲或折曲，但主体弯曲方向不变；③弯曲且方向不固定型，即弯曲方向不明，存在波动；④非常弯曲型，形态结构呈回形针状，符号化后容易出现图形冲突现象，如图8(b)所示。不同模式类型的道路曲线段，同样需要采用不同的化简算法。

图8 模式类别划分与人工标注案例Fig.8 Examples of line pattern types and manual labeling of administrative boundary and mountain road

2.2 样本数据生成与模型参数设置

构建的SCNN模型输入线元特征序列长度设置为224。采用滑动窗口和几何变换两种方法进行样本数据的生成与扩容。如图9所示，滑动窗口方法是在线状目标的起始点创建一个窗口，提取窗口内部的曲线段作为一个样本；然后，按照预设步长滑动窗口并重复上述操作，直至终止点被窗口包含。其中，窗口大小设置为与模型输入序列长度相一致，移动步长设置为20个线元。几何变换方法是对滑动窗口提取的曲线段进行旋转，以扩容样本。试验中，每个曲线段按间隔15°旋转得到一个新样本。最终，行政区界线训练数据集共形成4225个样本，道路训练数据集共形成5180个样本。对于参与测试的行政区界线或道路目标，按照输入序列长度进行切割形成测试样本。若样本包含线元数量达不到输入序列的长度要求，则通过零值填充方式补齐。最终，行政区界线测试数据集形成80个样本，道路测试数据集形成174个样本。

图9 样本数据生成与扩容Fig.9 Sample generation and augmentation

采用Adam算法[24]训练模型50轮，学习率为0.000 1，批次大小为32，随后对测试集进行测试。两种已有基于机器学习的分段方法被用于与本文方法进行对比，即BANN(backpropagation artificial neural network)方法[13]和NB(Naïve Bayes)方法[10]。这两种方法均利用移动窗口提取曲线段，采用线段长度与基线长度比、弯曲长度均值、转角均值等10个特征参量描述曲线段的形态结构[10]。其中，利用主成分分析方法选择信息量之和大于90%的描述特征作为机器学习模型的输入值。通过多次试验对比分析，行政区界线和道路目标的移动窗口大小与移动步长分别设置为1500、150 m和6000、600 m。BANN隐含层包含15个神经元，并采用ReLU激活函数，贝叶斯方法采用高斯模型。

2.3 试验结果与分析

首先，本文评估了行政区界线和道路测试数据中线元总体分类准确率，即正确分类的线元数量与线元总数的比率，分别为90.8%和85.8%，这表明本文构建的序列卷积网络可以较好地从样本数据中捕获线元的形态特征，实现较为准确的线元分类。不同方法对两组测试数据的最终分段结果如图10所示。

针对两组测试数据，3种方法都能根据形态特征进行有效分割，形成具备形态均质性的线段。对比BANN和NB两种方法，本文方法模式类别预测错误情况较少，分段较为准确。例如，图10(c)、(d)所示的行政界线数据分段结果中黄色椭圆标注区域，存在光滑型线段被对比方法预测为折线型模式，且表现出因依赖单个弯曲而不具备较大区域内的宏观性判断，而本文方法的分段结果更为合理，符合视觉认知；图10(g)、(h)中所示的道路数据分段结果中紫色椭圆标注区域，存在非常弯曲型线段被对比方法预测为弯曲且方向不固定型，而本文方法的分段结果与人工标注一致。此外，BANN方法和NB方法分段结果中存在不少零碎分割现象，例如图10(c)、(d)、(g)、(h)中绿色椭圆标注的区域，而本文方法通过迭代融合方法处理后可有效避免该现象。

图10 不同方法对两组测试数据的分段结果示例Fig.10 Comparison of the segmentation results of the two testing datasets obtained by the manual annotation and the three automatic methods

进一步地，采用一致性比率指标对不同方法的分段识别结果进行量化评价。对于某一模式类别i的分段一致性比率LAi，定义为

(7)

式中，L_correcti表示该类别曲线段被完全正确识别的长度；L_totali表示该类别曲线段的总长度。对于整体的分段一致性比率LA，定义为

(8)

式中，L_total表示测试集线状目标的总长度。

不同方法的整体分段一致性比率和不同模式类别的分段一致性比率统计结果见表1。分析发现，本文方法在两个测试数据集上取得的整体分段一致性比率均超过85%，相较其他两种方法有一定提升。具体来看，针对行政区界线数据，BANN方法和NB方法识别弯曲型曲线段的一致性比率都达到90%，略优于本文方法；但是对于光滑型和折线型曲线段，两种方法的一致性比率都低于本文方法。结合图10(a)—(d)分析也发现，这两种方法中大量的光滑型曲线段被错误地识别为折线型，特别是NB方法对光滑型曲线段的识别一致性比率仅达到48.87%。经统计，标注为光滑型的368.9 km曲线段中有181.1 km被划分为折线型。针对山区道路数据，本文方法对不同模式曲线段的识别都好于两个对比方法。但是针对光滑型的曲线段，3种方法的分类精度都相对偏低；对于非常弯曲型的曲线段，BANN方法和NB方法都容易错误地识别为弯曲且方向不固定型，如图10(g)、(h)中紫色椭圆标注区域。

表1 利用不同方法对两组测试集线状目标分段结果的评价指标统计Tab.1 Evaluation index statistics of the segmentation results for the two testing datasets using different methods (%)

2.4 讨论

上述试验结果表明，本文方法整体上优于基于BANN和NB模型的分段方法。这可能与常规机器学习方法要求人工选择特征描述参量有关。例如，采用基于弯曲结构定义的特征参量，适合于描述行政区界线上弯曲形曲线段形态变化，而对于光滑型和折线型曲线段则缺乏有效描述能力。本文方法则充分利用深度学习的深层次特征抽取能力，以线元为基本单位，以线元两侧端点的横纵坐标差作为特征描述，通过卷积神经网络表征高阶特征，从而避免人为选择特征描述参量带来的主观性，对不同尺度、不同类型的线状目标分段适应性更好。

但同时也发现本文方法在分段点的确定上相比于人工标注存在一定差异，主要包括两种情形：①部分不同模式类别的曲线段之间本身存在交界模糊的现象，如图11(a)所示，该种情形具备存在的合理性，对最终分段结果的影响较小；②不同模式类别的曲线段之间分界点明确且两侧线形差异明显，但是本文方法产生了错误的分段输出，如图11(b)所示，该情形与模型对边缘信息辨识能力不足有关，这也是本文方法所面临的难点问题之一。采取的措施包括在多个尺度范围提取特征并进行融合处理，但这会提升模型的复杂程度且降低计算效率，后续需要进行更加深入的研究。

图11 分段边界模糊的两种情形Fig.11 Examples of inaccurate segmenting boundaries

3 结论

本文设计了一种线元特征学习与模式分类预测的SCNN模型，并在此基础上实现形态异质曲线段的分割。该方法的创新之处在于：①将不规则的矢量线状目标组织表达为线元特征构成的序列，满足深度学习模型的规范性数据输入要求；②引入图像语义分割领域的思想，将线状目标分段问题转化为线元的模式分类问题，利用卷积运算实现邻域信息的集成与高层次特征的提取，从而提升模式识别与分段性能；③以线元两端点的坐标差作为输入特征，通过深度学习获取高层次的曲线段类别描述特征，有效避免人工选择特征带来的主观性影响。采用不同比例尺的行政区界线和山区道路数据进行试验验证，输出结果的分段一致性比率分别达到91.25%和85.65%，相比较基于传统机器学习的分段方法有一定提升。

后续工作将围绕以下几方面开展：①将本文方法应用到海岸线、等高线、单线河流等其他类型的线状目标，同时进一步扩展形态特征分类模式，更全面地考察本文方法的优势和不足之处，并更好地与后续地图数据处理操作(如综合化简)建立衔接关系；②改进SCNN模型，包括输入特征维度和网络层数的优化，以及其他激活函数的尝试等；③高质量的样本数据对基于深度学习的方法具有重要影响，后续将围绕不同语义类型的线状目标及不同的应用场景构建专门的样本数据集。