渐进性优化的尺度自适应Cauchy稳健估计模型及其应用
2023-02-18李加元张永军艾明耀胡庆武
李加元,张永军,艾明耀,胡庆武
武汉大学遥感信息工程学院,湖北 武汉 430079
稳健估计是几何处理与平差系统中的一个核心基础问题[1-5],在摄影测量与遥感、计算机视觉、机器人视觉等领域发挥着重要作用。它是一种同时进行几何模型拟合与异常值检测的技术,能够从被污染的观测值中正确估计出观测值所满足的几何模型。由于实际观测值中不可避免地存在粗差(异常值),该技术已被广泛应用于误匹配剔除[6]、光束法平差[7-8]、点云配准[9-10]、同时定位与制图(simultaneous localization and mapping,SLAM)[11]等摄影测量任务中。基于M估计的迭代加权最小二乘(iterative reweighted least squares,IRLS)[12-19]和随机采样一致性方法(random sample consensus,RANSAC)[20-27]为最常采用的两类稳健估计方法[28]。
IRLS又称选权迭代法[12-13],相比RANSAC类方法,其优点是运算效率高并且能够确保局部最优解[28],IRLS通常采用M估计作为稳健核函数。在迭代过程中,IRLS的核心思想是基于观测值残差赋予粗差小权值,可靠观测大权值,从而缓解粗差对平差系统的影响。IRLS的关键在于权函数的选取,常用的权函数包括Huber、Cauchy、Welsch、Tukey等M估计核[13]。文献[15]基于验后方差估计思想推导权函数。文献[16]提出一种基于IGG(institute of geodesy and geophysics)权函数的迭代加权总体最小二乘法。文献[18—19]分别从效率与稳健性方面对传统M估计进行改进。IRLS及现有变种都存在一个严重缺陷,即IRLS在理论上无法处理高于50%的粗差。一旦观测值中粗差比率高于50%,此类方法完全失效。随着自动化处理的普及,观测值包含50%粗差的情形随处可见,如影像特征匹配、点云特征匹配、SLAM闭环检测等。因此,在这些任务中,对高粗差比率较为稳健的RANSAC方法更受青睐。
RANSAC是一种假设检验技术[20],它主要包括两个步骤:①基于随机最小子集的几何模型估计;②基于一致性集的几何模型验证。RANSAC交替执行上述两个步骤直至满足终止迭代条件,对应于最大一致性集的几何模型被认为是正确解。RANSAC存在大量改进算法[21-27]。MLESAC(maximum-likelihood estimation by random sampling consensus)[21]基于概率统计思想,采用最大化似然性来取代RANSAC方法的最大化一致集大小。LO-RANSAC(locally optimized RANSAC)[22]和FLO-RANSAC(fixing locally optimized RANSAC)[23]通过增加局部优化过程来减少所需的采样次数。GC-RANSAC(graph-cut RANSAC)[24]通过引入图割技术来进一步提高局部优化的可靠性。RECON(residual consensus)[25]利用残差一致性来消除RANSAC对内点阈值的依赖性。USAC(universal RANSAC)[26]将多种改进算法的特性纳入一个通用框架内,包括工程及计算等方面的技巧。MAGSAC++(marginalizing sample consensus)[27]提出一种独立于内点阈值的打分函数。但是,RANSAC类方法存在3大缺点:①采用最小集估计几何模型仅能获得近似解,最优解需全部观测值参与解算;②随着粗差比率的增加,此类方法的时间复杂度呈指数增长,运行效率低下;③RANSAC类方法难以直接应用于测量平差系统中。
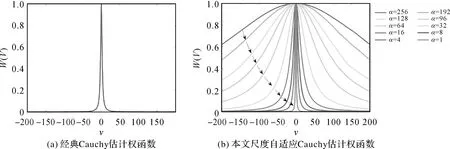
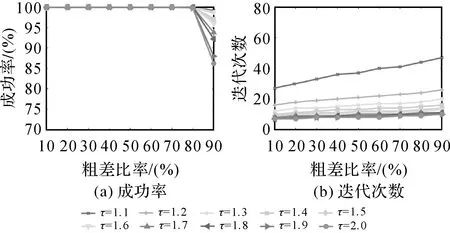
近年来,许多研究工作试图突破上述M估计的瓶颈问题。例如,M估计被pbM估计器[29]和广义pbM估计器[30]重新表述为基于投影的优化问题,并基于变量误差(EIV)模型进行求解。加权Q范数[31]估计器进一步提高了Q范数模型(0 本文旨在构建一种同时继承IRLS的优点(高效且最优)与RANSAC的优点(能处理高于50%的粗差)的模型,提出了基于渐进优化的尺度自适应Cauchy稳健估计模型(注:本文所提尺度自适应模型具有通用性,并不仅限定于Cauchy估计,也适用于Huber、Tukey等M估计)。所提模型引入尺度因子来不断过滤大残差观测值并调节Cauchy核函数的稳健性,采用由粗到精的方式进行渐进优化。与前期工作[33]的不同之处主要表现为两个方面:①本文模型与统一代价函数的数学模型不同。本文模型是M估计模型的推广,为非分段函数,不存在奇异点问题;②在模型优化求解过程中,每次迭代利用控制参数剔除一部分大残差观测值,因此,在本文的优化过程中,观测值是动态变化的。而在统一代价函数模型中,尽管观测值在某次迭代中获取了很小的权值,但在后续迭代中有可能重新获得较大权值,导致迭代震荡现象。此外,本文还给出了其在经典摄影测量任务中的应用,包括匹配剔除、后方交会及点云配准。试验结果表明,该模型明显优于基于M估计的IRLS模型和RANSAC类方法。 M估计是最大似然估计的泛化形式,其数学表达如下(以线性回归为例) (1) 式中,ρ(vi)为稳健核函数,vi=(f(xi,θ)-yi)为观测值(xi,yi)的残差;f(·)是观测值所满足的几何模型(此处为线性模型);θ为待求模型参数;N为观测值数目。 表1 常用的M估计核函数ρ(v)和权函数w(v)(v为观测值残差,c为常量)Tab.1 Several commonly used M-estimators and their weight functions (v is the residuals of observations,c is a constant) 式(1)通常转换为下述IRLS问题进行求解 (2) (1) 变量估计:给定权值w(vi)t-1作为已知量(t为迭代计数器),采用加权最小二乘法求解问题(3) (3) (3) 交替迭代执行步骤(1)和(2),直至满足算法终止条件。 动机:经典Cauchy估计只能处理低粗差比率问题。如果粗差比率较高(>50%),则初始估计(首次迭代)模型将大幅偏离真值,从而造成正确观测值的残差较大,权重很小。图1(a)为经典Cauchy估计的权函数,可以看出,当残差为20时,其权重仅为0.01。在如此苛刻的条件下,许多正确观测值并没有实际参与优化过程。因此,理想的稳健估计代价函数应该首先让所有观测值都参与到优化过程,然后,随着迭代的进行逐渐提高代价函数的稳健性,最终变为经典的M估计函数。具体如图1(b)所示,观测值取得小权值(假设为0.01)所对应的残差阈值应随着迭代的进行不断缩小。开始时所有观测值都参与优化,尽管初始模型可能不准确,但残差较大的正确观测值仍会对优化过程做出较大贡献。每次迭代后由于阈值减小,一部分具有最大残差的观测值将会被赋予小权值,这些具有最大残差的观测值通常都是粗差观测。因此,随着代价函数的变化,许多粗差观测被剔除,真实的粗差比率会不断降低。当代价函数变为经典M估计时,真实粗差比率将会小于50%。 图1 传统Cauchy M估计与理想稳健估计的权函数曲线对比Fig.1 Comparison of traditional M-estimation function and the ideal function for robust estimation 模型:为实现上述过程,本文提出了尺度自适应Cauchy稳健估计模型。在经典Cauchy估计中引入尺度参数α来控制代价函数的稳健性,其数学公式为 (4) 与其对应的权函数为 (5) 图1(b)显示了不同尺度下的权函数曲线。可以看到,当α取值越大时,越多的观测值能够参与优化过程;反之,当α取值越小时,只有残差很小的观测值参与优化,模型估计精度越高。 求解:所提模型为经典M估计的变种,可采用“由粗到精”的IRLS优化策略。首先,将α初始化为大值(本文将初始尺度α0设为初始估计模型的最大残差),进行模型估计、粗差剔除和权值更新;然后,随着迭代过程α不断减小,并执行上述步骤直至模型收敛。 (1)变量估计:给定尺度αt-1和观测值权值w(vi,αt-1)t-1作为已知量,采用加权最小二乘法求解问题,见式(6) (6) (3)尺度更新:减小尺度αt=αt-1/τ,其中τ为步距常数(本文设为1.3)。 (4) 交替迭代执行步骤(1)—(3)直至满足终止条件。 可以看出,所提模型的优化过程与传统IRLS相似,仅多出粗差剔除与尺度更新过程。因而,其也具有传统IRLS方法的优点,如优化效率高、具有最优解、适用于平差系统等。 稳健估计在摄影测量与遥感任务中具有重要作用,本节将所提尺度自适应Cauchy模型应用于误匹配剔除、相机位姿估计及点云配准中。 yi=f(xi,θ)=Axi+t (7) 式中,A为2×2仿射矩阵;t为2×1平移向量;θ=(A,t)为仿射变换模型参数。误匹配剔除的尺度自适应Cauchy权函数为 (8) (9) 式中,P=K[R,T]为3×4相机投影矩阵;Pk(k=1,2,3)为P的第k行;θ=(R,T)为位姿参数。 后方交会的尺度自适应Cauchy权函数为 (10) Yi=f(Xi,θ)=RXi+T (11) 式中,θ=(R,T)为配准参数;R为三维旋转矩阵;T为三维平移向量。 误匹配剔除的尺度自适应Cauchy权函数为 (12) 如果在模型f中加入尺度因子,该问题即变为摄影测量中经典的绝对定向问题。 采用模拟试验和真实数据试验来评估本文模型的稳健性、精度及效率。基于误匹配剔除、相机位姿估计及点云配准3个任务,将所提模型与Cauchy估计、Welsch估计、RANSAC、FLO-RANSAC及MAGSAC++进行对比分析。试验选用均方根误差(RMSE)、成功率及运行时间作为定量评价指标。每种方法的详细配置信息(参数与代码来源)见表2。所有方法的运行时间均在单核1.8 GB赫兹CPU i7-8550U上统计得到。 表2 对比方法参数设置与代码实现Tab.2 The parameter settings and implement details of each compared method 试验结果如图2所示,Cauchy和Welsch估计在粗差比率低于50%的情况下精度与速度均为最优。但是,一旦粗差比率超过50%,其性能将急剧下降,成功率曲线现断崖式下跌至0。这也与M估计在理论上只能处理低于50%的粗差观测的结论相吻合。与M估计相比,RANSAC类方法(RANSAC、FLO-RANSAC和MAGSAC++)和本文模型则对高粗差比率较为稳健,能处理高达90%的粗差观测。由于RANSAC类方法无法获得最优解,RANSAC和FLO-RANSAC的模型估计精度相对较差(RMSE最大)。虽然MAGSAC++也是RANSAC的一种变体,但是其在算法中采用了M估计来提升模型精度。本文方法精度与M估计相当,运行效率仅次于M估计。在粗差比率为90%时,本文模型比RANSAC方法快将近3个数量级,比采用C++实现的MAGSAC++快将近2个数量级。 图2 误匹配剔除模拟试验结果Fig.2 Comparison of mismatch removal results on the simulated data 真实试验:选取6种类型(包括可见光-可见光、红外-可见光、SAR-可见光、深度图-可见光、地图-可见光、夜光-白天)的多模态影像对进行试验对比。本文采用RIFT算法提取初始匹配点集。由于多模态影像存在严重的非线性辐射畸变,初始匹配点的粗差比率较高(>80%),传统M估计无法成功解算,故只与其他3种方法进行对比,试验结果见表3。本文模型同时取得了最佳模型精度与运行速度。模型精度相比排名第二的方法提升了15.6%;运行效率比采用C++实现的MAGSAC++快25倍,比RANSAC和FLO-RANSAC快350多倍。本文模型在每种影像对上的定性定量结果如图3所示。 表3 误匹配剔除真实试验结果Tab.3 The results of mismatch removal on real data 注:n为初始匹配数量,γ为粗差比率,黄线表示正确匹配对。图3 本文方法在多模态影像上的匹配结果Fig.3 Our feature matching results on the multi-modal image dataset 图4 后方交会模拟试验结果Fig.4 Comparison of image orientation results on the simulated data 真实试验:选用2张由SWDC倾斜相机所摄影像作为测试数据,影像大小为5406×7160像素,摄影比例尺约为1∶8000,相对航高接近700 m。其中,第1幅影像由中心垂直摄影相机拍摄所得,焦距为12 102.1像素;第2幅影像由倾斜摄影相机获取,焦距为14 671.5像素。采用GPS-RTK技术在第1幅影像覆盖测区内布设了36个控制点,第2幅影像测区布设了60个控制点。然后,由人工刺点方式获取这些控制点所对应的像点坐标。然而,由于人工刺点错误,两幅影像中正确像点观测个数分别仅为12和15,即两幅影像的粗差比率分别为66.7%和75%。实现结果见表4,本文方法再次在RMSE和运行时间两个指标上取得了最优,解算精度约为1个像素。 表4 后方交会真实试验结果Tab.4 The results of image orientation on real data 模拟试验:模拟过程与误匹配剔除类似,不同之处在于点云配准的观测值为三维坐标点,并且几何模型为仅包含三维旋转和平移的刚体变换。三维点由正态分布N(0,1002)获得,旋转角在区间[-π/2,π/2]内随机生成,平移量在区间[-100,100]内生成,高斯噪声标准差为0.1 m。试验结果如图5所示,M估计(Cauchy和Welsch)在粗差比率超过40%后,性能开始急剧下降。反观本文方法,即使在90%的粗差比率下,其解算成功率依然接近100%。 图5 点云配准模拟试验结果Fig.5 Comparison of point cloud registration results on the simulated data 真实试验:从ETH公开激光点云数据集中选取3个点云匹配对进行试验,每个匹配对间的真值刚体变换已知。这些激光点云的数据量非常大(千万级点数),因此,首先利用格网滤波方法进行降采样,采样间隔为0.1 m。然后,采用ISS(intrinsic shape signatures)[36]算法和FPFH(fast point feature histograms)[37]算法分别进行特征检测与特征描述,并通过最近邻匹配得到初始3D特征匹配点。由于激光点云缺乏纹理信息,3D特征描述符的显著性比较差,所以初始匹配集中粗差比率非常高(本文试验中>96%)。在进行算法对比试验之前,首先基于支持线投票策略进行初步筛选,过滤掉部分粗差观测。试验结果见表5,可知,本文模型的配准精度达到了0.2 m(两倍的点云分辨率)。除开预处理部分(降采样、初始匹配、支持线投票)的耗时外,本文模型仅需0.02 s即能实现配准参数解算。详细的定性定量结果见图6。 表5 点云配准真实试验结果Tab.5 The results of point cloud registration on real data 注:n为初始匹配数量,γ为粗差比率,绿线表示正确匹配对。图6 本文方法在三维激光点云上的配准结果Fig.6 Our registration results on 3D LiDAR point clouds 基于点云配准模拟试验来分析步长参数τ的最佳取值,试验过程与3.3节类似,区别在于步长参数τ的取值不同,试验结果如图7所示。 由图7可知,当粗差比率小于80%时,τ在1.1~2.0间取值时均能取得100%的成功率;当粗差比率大于80%时,τ的取值越大,成功率越低。而算法所需的迭代次数与τ成反比,即τ越小,迭代次数越多,计算效率越低。综合成功率和效率因素,τ的建议取值范围为1.3~1.6,本文取1.3。 图7 参数τ敏感性分析试验结果Fig.7 Results of sensitivity analysis of parameter τ 本文模型存在一个隐含假设前提,即粗差观测近似满足均匀或者随机分布(非对抗性粗差,non-adversarial outliers)。如果该假设前提不成立,则本文模型可能失效。比如,当粗差观测大于50%,并且它们之间也满足另一个几何模型时,本文模型的解算结果将为粗差观测所满足的几何模型。因此,其不适用于多几何模型同时估计的情形。再比如,当正确观测与粗差观测在空间分布上各自聚为一团,并且相距较远时,那么,由于初始估计偏差过大可能导致模型无法收敛。解决该类问题只需提供待求模型的良好初值。 本文提出了一种渐进优化的尺度自适应Cauchy稳健估计模型。该模型引入了尺度控制参数来调节经典Cauchy核函数的稳健性。此外,该参数还发挥内点阈值的作用。在优化过程中,采用粗到精的迭代加权最小二乘法(IRLS)不断提升核函数的稳健性并过滤掉大残差观测值,降低真实粗差比率。采用大量模拟与真实数据对本文模型的正确性、解算精度、运行效率、通用性进行验证,得到以下几点结论: 与采用M估计作为核函数的IRLS方法相比,本文模型能处理高粗差比率的情形。与RANSAC类方法相比,本文模型能获取最优解,模型求解精度更高,并且运行效率提升了2~3个数量级。本文模型具有较好的通用性,在误匹配剔除、后方交会和点云配准任务中均取得了很好的效果。综上所述,笔者认为该模型具有很好的实用性,在大多数摄影测量、计算机视觉等任务中能够取代已被广泛应用的RANSAC方法。 因为本文模型与经典选权迭代法在形式上保持一致,笔者相信本文模型亦能用于平差系统中,进一步提升现有平差系统的抗差性能,这将是笔者下一步的研究重点。此外,IRLS方法比牛顿法的收敛速度慢,在高维度问题上尤为突出,后续笔者将进一步研究基于牛顿法的稳健估计模型[38],提升平差系统运行效率。1 经典M估计与IRLS




2 尺度自适应Cauchy稳健估计模型

3 模型应用
3.1 误匹配剔除

3.2 后方交会
3.3 点云配准

4 试验结果与分析

4.1 误匹配剔除
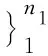



4.2 后方交会




4.3 点云配准



4.4 参数τ敏感性分析
4.5 模型缺陷
5 结 论
