基于高参数均匀性的叶片曲面光顺造型方法*
2023-02-18陈志同
田 野,宁 涛,陈志同
(1.北京航空航天大学机械工程及自动化学院复杂曲面先进加工技术实验室,北京 100191;2.北京航空航天大学机械工程及自动化学院飞行器制造工程实验室,北京 100191)
复杂曲面类零件被广泛应用于航空发动机、直升机螺旋桨、汽轮机、汽车精密模具等关键部件的生产制造中。航空发动机具有高复杂度和高精密性的特点,其制造技术是国防实力的重要衡量标准。航空发动机叶片的质量很大程度上决定了发动机的核心性能。叶片曲面的光顺造型对后续的加工流程极为重要,光顺的曲面造型更有利于生成平滑的刀轨,提高加工精度与加工效率。因此叶片的曲面造型不是仅停留在对数据点的简单拟合来获得其大致外形,更重要的是对数据点进行一系列的优化,自动快速地获得光顺曲面。国内外学者关于曲面的光顺造型开展了一系列研究。
在叶片光顺曲面造型方面,根据叶片几何特征间约束的表达可分为基于曲线变形的曲面造型方法与基于曲线拟合的曲面造型方法。曲线变形方法包含七段圆弧法、非刚性配准法、分段高斯映射法等。七段圆弧法最早由Mohaghegh 等[1]提出,通过单层二维截面上数据点的划分来拼接构造七段圆弧以获得完整截面轮廓线。从特征约束的角度出发,Mohaghegh 等[2]提出了叶片曲面重构的3 个基本步骤来构造叶片曲面。Piya 等[3]提出分段高斯映射法并在机翼上应用且取得了成功。Li等[4]提出的非刚性变形配准方法可在一定的精度条件下重构多层截面轮廓线。Zhao 等[5]提出基于自由变形的叶片截面线重构方法重构截面轮廓线。曲线拟合方法中较有代表性的方法为Werghi 等[6–7]提出的直线和圆弧特征在叶片截面轮廓线中的约束拟合法。Ke 等[8]提出了基于B 样条等自由曲线的约束拟合方法。Khameneifar 等[9]给出了基于数据点不确定度的最小波动线拟合方法。
在曲面造型这一领域,国内也进行了相当多的研究工作。莫堃等[10]提出了结合流场约束的隐式曲面重构方法,保证了重构曲面的几何精度要求。吕学庚[11]提出一种航空发动机叶片流曲面重构方法,降低了叶片曲面重构的不确定性。曲学军等[12]利用统计学知识给出了平面轮廓线数据的B 样条曲面拟合算法并对平面轮廓线扫描数据进行B 样条曲面拟合。张云[13]给出了一种改进的中弧线–厚度分布方法,可用于精锻叶片自适应重构。施恒涛等[14]提出了一种基于多项式的曲率连续前缘造型方法,通过给定叶片前后缘和叶身交点过渡部分的中弧线和厚度分布的各阶导数来保证截面轮廓线曲率连续。周承号等[15]对点云数据进行数据处理,并对数据进行了流场的数据模拟,完成了涡轮叶片的曲面造型。黄攀[16]基于叶片二维翼型及三维叶片泛函集成表达理论,利用NURBS 节点控制向量构建了风力机叶片曲面模型。
上述研究中依旧存在一些问题,具体表现在:(1)通常将每层截面轮廓线作为整体来进行优化,生成的整张封闭曲面往往需要在调整数据点位置时,同时控制其逼近精度,导致算法异常复杂,影响在实际工程中的应用;(2)忽视了参数均匀性对叶片曲面造型的影响,除了沿截面轮廓线的周向参数外,叶片曲面沿径向的参数均匀性也会很大程度上影响曲面质量。
为了进一步解决由于参数不均匀导致的曲面不光顺问题,本文提出了一种基于高参数均匀性的叶片曲面光顺造型方法:(1)通过生成4 张曲面以代替整张封闭曲面,实现了对叶片造型过程的解耦,避免叶片边缘过渡部分与叶身的过度约束;(2)以弧长参数化方式构造关键曲线,在保证造型精度的前提下使多层截面轮廓线光顺,达到叶片周向和径向同时参数均匀对齐的效果,提升了曲面的光顺程度;(3)用户输入数据点,应用优化算法即可高效自动地生成光顺叶片曲面,极大程度上简化了叶片的建模流程。通过对某型号发动机叶片数据点进行曲面造型与实际加工,对提出方法进行了验证。
1 基于高参数均匀性的叶片曲面光顺造型方法
在航空发动机叶片模型构造过程中,可能会面临两方面问题。(1)初始数据点通常沿径向分层分布,每一层数据点均位于同一平面上,层与层之间相互平行。在构建叶片截面轮廓线时,如直接用封闭曲线拟合,在首尾相接处极易出现不光顺现象,边缘部分曲率变化越剧烈,得到封闭曲线的精度越低,进而导致构造的曲面发生扭曲或自交叉。(2)目前曲线的参数化方式多为积累弦长参数化,在数据点曲率变化较大的部分,实际弦长与实际弧长的差值变大,故需要对积累弦长参数化方法进行改进以提高参数均匀性,具有高均匀性的参数可以保证叶片曲面各层截面轮廓线的周向和径向参数准确对齐,避免曲面起伏或局部厚度变化而导致整体造型结果不理想,本文提出一种叶片曲面光顺造型方法。算法输入为叶片初始数据点信息,通过数据预处理进行初步区域划分,进而利用样条拟合以及非线性方程组的迭代求解获取关键曲线参数,进而结合中弧线–变半径厚度圆的曲线包络理论生成光顺叶片曲面,整体构造流程如图1所示,需要说明的是,每个前置条件衍生出的所有后置条件均需全部满足,才能进入下一流程。

图1 叶片光顺曲面造型流程Fig.1 Process of blade smooth surface modeling
1.1 光顺叶片截面轮廓线的快速生成
1.1.1 诱导曲线的构造
本文采用中弧线–厚度分布函数的形式来生成叶片截面轮廓线,在输入仅有数据点的前提下,首先将数据点大致分为叶盆、叶背、前缘、后缘4 个部分,叶盆曲线与叶背曲线统称为叶身曲线,对前缘和后缘部分的数据点分别进行最小二乘圆弧拟合,得到其拟合圆圆心;接着对叶身部分的数据点进行样条拟合,以获得叶身曲线的大致轮廓;最后由两拟合圆圆心以及其连线的中垂线与叶身曲线的两个交点的中点生成中弧线的诱导曲线。诱导曲线生成算法具体步骤如下。
(1)将数据点分为左右两个半区,需要先获取这组数据点集的最小二乘直线。对于同一平面上的数据点集,最小二乘直线是指已知的数据点集到该直线距离的平方和最小,即具有最小二乘解。在获得最小二乘直线LALB后,可以获取数据点集中距离最小二乘直线距离最大的测量点,记为PA,过PA做Y轴的平行线LP,找到数据点集中距离LP最近的一点,记为PB;以PA和PB将数据点分为左右半区,申请两组容器pntsL和pntsR 来储存左右半区的数据。
(2)为将数据点分为叶盆、叶背、前缘、后缘4 个区域,需要选取4 个特征点。首先找到数据点的精确公切线,由于仅寻找公切线,会有很多可行解,因此需要加上一个限制条件:两个切点分别位于左右半区的下侧。得到的精确公切线CT 和切点PCL、PCR,如图2所示,选取PCL、PCR作为两个特征点。利用已获取的公切线,遍历数据点集,寻找左右半区两端在公切线方向向量上投影的极值点作为另外两个特征点,文中取x坐标的极大值点PM与极小值点PN,图3给出了后缘部分的特征点PN。获取了全部4 个特征点后,将数据点集分为4 部分并存储在4组容器中,后缘、叶盆、前缘和叶背部分数据点分别对应存储容器pnts1、pnts2、pnts3 和pnts4,点区间的选取规则为左闭右开。
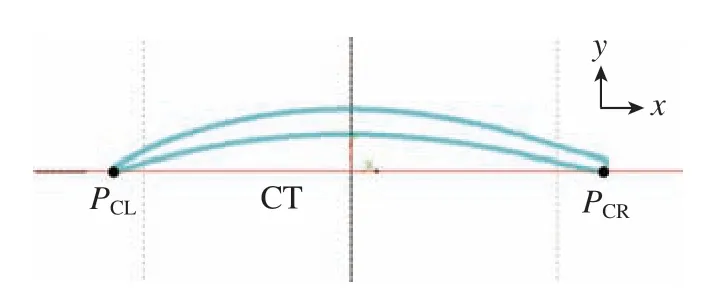
图2 截面轮廓线数据点的精确公切线Fig.2 Exact common tangent of contour data points
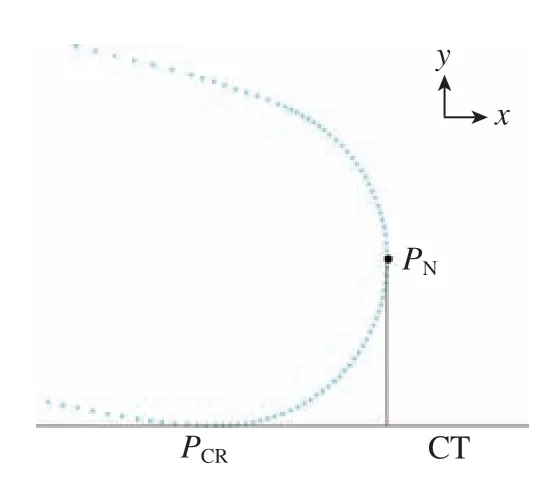
图3 后缘部分的特征点Fig.3 Feature points of trailing edge
(3)利用步骤(2)存储容器pnts1和pnts3 中的点进行最小二乘圆弧拟合,得到叶片前缘与后缘部分的最小二乘拟合圆弧。值得注意的是,进行一次拟合很难满足精度要求,因此需要给定一定的容差δ来进行迭代拟合,容差由叶片造型允许误差决定。得到满足精度要求的最小二乘拟合圆弧后,可以获得两侧的圆弧圆心,记为O1和O2。
(4)利用步骤(2)存储容器pnts2和pnts4 中的点,以样条插值方式得到近似的叶身曲线,记为CA和CB。连接O1和O2,得到线段并计算出其中垂线T,中垂线T与CA、CB分别交于PU和PD两点,取PU和PD的中点,记为PO;以O1、PD、O23 点插值出诱导曲线LG,如图4所示。
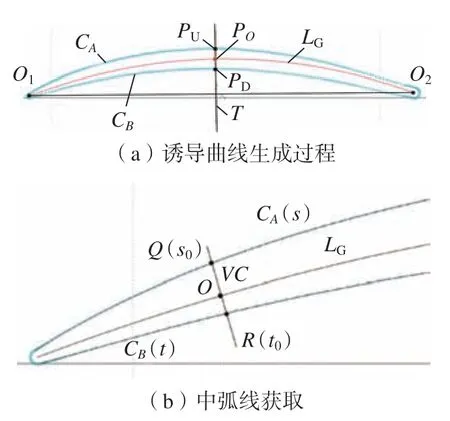
图4 精确中弧线的获取Fig.4 Generation of accurate camber curve
1.1.2 弧长参数化方式光顺中弧线的获取
根据1.1.1 节中生成的诱导曲线,利用改进的牛顿迭代法生成初始中弧线,进而对中弧线进行弧长参数化,最后进行给定容差的光顺处理,可以得到容差范围内的光顺中弧线以及厚度分布函数。
诱导曲线的参数区间Interval 为u∈[0,1],在诱导曲线上按照一定的步长取点,过这些点分别作诱导曲线的垂线,内切圆圆心一定在垂线上。叶背曲线CA的含参数表达式为CA(s),叶盆曲线CB的含参数表达式为CB(t),O(x0,y0)为诱导曲线上的点,将其作为内切圆圆心的初始点,内切圆半径为r0,其初始值设为左侧最小二乘圆弧的半径,直线VC为过O点的诱导曲线的垂线且满足方程Ax0+By0+C=0,Q(s0)与R(t0)分别为VC与CA和CB的交点,将其作为切点初始值;CA'(S0)和CB'(t0)为曲线在该处的切矢,则可列出非线性方程组,即

通过具有预估–校正格式的改进牛顿迭代法可求解上述非线性方程组,初始值上文已经给出。通过试验得知,上文的初始值迭代运算次数一般在3 次以内,可以快速收敛至近似解。可以得到一系列内切圆圆心{Oi}以及内切圆半径{ri},i=0,1,…,n,其中,n为按给定步长选取的参数点数量,进而利用3 次样条插值的方法获得精确中弧线,其参数表达式为MCac(u)。对生成的精确中弧线进行光顺处理和弧长参数化,首先利用改进的能量法,对中弧线进行给定容差的光顺处理,得到更加平滑的中弧线,按示例叶片的加工要求,建模允许误差应比最大允许加工误差降低一个数量级,因此其偏差控制在0.001 mm 以内,针对不同叶片的加工要求,光顺偏差可灵活调整,图5给出了光顺前后的中弧线曲率梳分析。
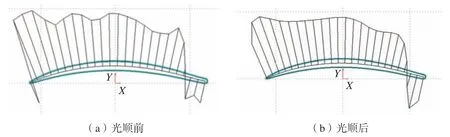
图5 中弧线曲率梳分析Fig.5 Analysis of curvature combs of camber curve
目前曲线的参数化多为积累弦长参数化方式,即用弦长近似代替弧长,这种参数化方式在参数的末端边界部分会产生较大的积累误差。为了消除由于算法本身所带来的误差,对光顺中弧线进行重新参数化,即由积累弦长参数化转变为弧长参数化。具体分为以下4 个步骤。
(1)计算出光顺中弧线的总弧长,然后按照上文给定的参数步长在中弧线上取点,记录下这些数据点{Di},以及对应中弧线上的参数{ui},其中,i=0,1,…,n。
(2)依次计算从中弧线起始点到数据点{Di}的弧长与曲线总弧长的比值,以这个比值来代替原先的参数,记为{ui'},i=0,1,…,n。
(3)计算{ui'}与{ui}的差值,当所有差值均小于给定容差 (针对文中算例,容差取10–6mm)时弧长参数化结束,令ui=ui',否则回到步骤(1),直到满足差值小于给定容差,其中,i=0,1,…,n。
(4)用给定点串和参数的方式插值步骤 (3)中最终得到的数据点,其参数和节点矢量均固定,最终得到弧长参数化的光顺中弧线MC(u)。
1.1.3 光顺叶片截面轮廓线生成
在生成弧长参数化的光顺中弧线后,首先利用中弧线–厚度分布函数的方式构造叶身曲线,然后在叶片截面轮廓线的前缘和后缘部分生成过渡曲线,并保证过渡曲线与叶身曲线G1连续,最终得到光顺的叶片截面轮廓线。具体实现步骤如下。
(1)求解厚度分布函数。对内切圆半径集合{ri},其中,i=0,1,…,n以及1.1.2 节中最终得到的中弧线上的参数集合{ui}进行3 次样条插值可以得到r–u曲线,即厚度分布函数曲线。
(2)厚度分布函数曲线的光顺与弧长参数化。利用改进的能量法,对步骤 (1)中生成的r–u曲线进行给定容差的光顺处理,得到更加平滑的中弧线,其偏差控制在0.001 mm以内。利用与1.1.2 中相同的弧长参数化方法对厚度分布函数曲线进行弧长参数化。图6给出了光顺前后的厚度分布函数曲线以及以曲率为参数的曲率梳分析。
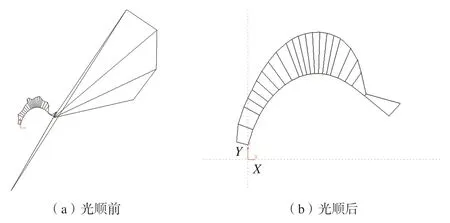
图6 厚度分布函数曲线曲率梳分析Fig.6 Analysis of curvature combs of thickness distribution function curve
(3)生成叶身曲线。利用1.1.2中得到的中弧线MC(u)以及步骤(2)中得到的光顺厚度分布函数曲线生成叶身曲线。首先计算一系列内切圆圆心,中弧线起点记为O0MC,其参数u0MC=0,终点记为O1MC,其参数u1MC=0,取参数中点=(u0MC+u1MC),然后得到对应内切圆圆心,计算到O0MC与O1MC连线之间的距离,当距离大于给定容差时 (针对文中算例,容差取10–4mm),记分别为O3MC、u3MC,O3MC将中弧线分为两部分,对这两部分中弧线重复上述过程,直至所有相邻3 个内切圆圆心均小于给定容差,计算结束。
最终得到内切圆圆心集合{OiMC},以及对应中弧线上参数{uiMC},i=0,1,…,p。其中,p为最终得到的内切圆圆心数量。
通过上述计算得到的厚度分布函数曲线方程以及一系列内切圆方程可以看作单参数曲线族F(x,y,c)=0,其中,c为参数,对应中弧线上的参数u,F(x,y,c)对x,y,c连续可微。由包络曲线的定义可以得到

在式(2)中消去参数而得到的方程F(x,y)=0,所表示的曲线即为单参数曲线族F(x,y,c)=0 的包络曲线。依此求解可得到叶盆和叶背上的点,然后利用样条插值得到叶身曲线,如图7所示。

图7 叶身曲线Fig.7 Profile of blade
(4)生成过渡曲线。在得到叶身曲线后,需要生成前缘和后缘部分的过渡曲线,可得到完整的叶片截面轮廓线;下文以生成叶片的前缘过渡曲线为例,后缘部分的过渡曲线生成方法完全相同。分别取叶身曲线的左端点M和N作为生成过渡曲线的两个控制顶点,并生成端点在曲线处的切线TM和TN,过1.1.1 节中步骤 (3)得到的拟合最小二乘圆弧的所有数据点做两条切线的投影,在TM和TN上找到距离叶身左端点最远的投影点VA与VB,以此作为拟合过渡曲线的另两个控制顶点。
以4 个控制顶点M、N、VA、VB生成3 次Bezier 曲线作为初始过渡曲线,为保证生成的过渡曲线与叶身曲线的连续性,将3 次Bezier 曲线进行两次升阶操作,即5 次Bezier 曲线;对5 次Bezier 曲线以1.1.1 节中步骤(3)得到的拟合最小二乘圆弧的数据点为参考点进行迭代的逼近与光顺处理,直至过渡曲线与叶身曲线的搭接部分误差小于10–8mm,以得到与叶身曲线G1连续的过渡曲线,如图8所示。
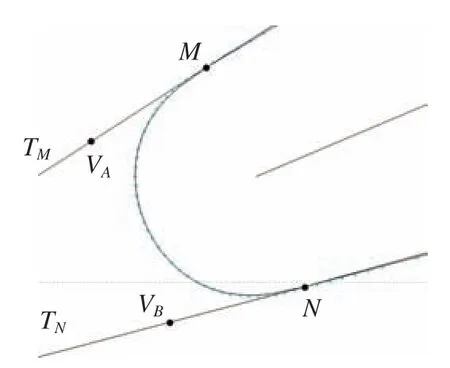
图8 过渡曲线的生成Fig.8 Generation of transition curve
值得指出的是,若直接用拟合最小二乘圆弧的所有数据点进行迭代逼近与光顺处理,会面临点串越界的情况,即部分数据点位于M和N的右侧,因此在进行逼近和光顺之前,对拟合最小二乘圆弧的数据点集进行了处理,剔除掉越界的点。
1.2 光顺叶片曲面的生成
1.2.1 叶身曲面造型
在得到光顺的叶片截面轮廓线后,通过曲面放样可获得叶盆和叶背两张曲面。曲面放样中沿v方向参数化的具体方法:对1.1.3 节中生成的叶身曲线进行反算,得到其B 样条的控制顶点,如图9所示,以叶盆曲线的一部分为例,RB 和RB'为相邻两层叶盆曲线的一部分,{CPi}和{CPi'}(i=0,1,…,6)为对应的控制顶点,求解相邻两层对应的控制顶点之间的实际距离占所有不同层对应控制顶点的实际距离之和的比例作为v方向的控制参数。由于同一层截面线上的控制顶点均在同一平面上,且经过1.1.3 节中步骤(3)的算法处理,所有的叶身曲线非常接近于弧长参数化,极大地减小了积累弦长参数化引起的不同层截面线之间的u方向误差,因此可以确保v方向的参数对齐且不会出现参数曲线扭曲的情况,生成的放样曲面如图10所示。
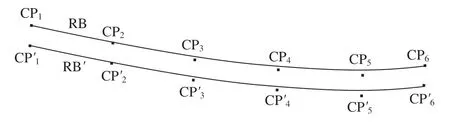
图9 反算B 样条的控制顶点Fig.9 Inverse computation of B-splines control points

图10 放样曲面Fig.10 Lofted surface
1.2.2 前后缘过渡曲面造型
拾取两张曲面,两条脊线和多条过渡曲线进行融合操作。以前缘过渡曲面生成为例,其具体步骤如下。
(1)如图11所示,拾取叶盆曲面SE 和叶背曲面SX,以两曲面的左边界SC 与SC'作为前缘过渡曲面的脊线,相邻两层过渡曲线为TC0与TC1。TC0与SC、SC'交于IP0、IP0'并取连线的中点O0作为原点,过O0作平面PV垂直于线段IP0IP0',过IP0作SC的切线T0,过IP0'作SC'的切线T0',将T0与T0'求平均并投影到平面PV,投影所得向量为x轴,以平面PV中x轴的垂线方向为z轴,利用右手定则得到y轴建立局部坐标O0xyz。同样的方法用于TC1建立局部坐标系O1xyz。

图11 融合曲面Fig.11 Blend surface
(2)取曲线SC 在IP0与IP1之间的部分取参数中点,得到IP2,对SC'采用相同的策略,获得IP2',用步骤(1)中的方法建立局部坐标系O2xyz,将TC0与TC1在O2yz面内的投影曲线进行加权平均,并对其添加限制条件,令其两个端点分别与IP2、IP2'两点重合,且端点处与SE、SX 与O2yz平面的交线保持G1连续,利用迭代逼近的方法得到插值曲线TC2。
(3)对全部相邻的过渡曲线重复步骤 (2),直至满足密度要求,得到曲线组{TC0,TC1,…,TCn},其中,n为给定曲线密度,以得到的曲线组生成平滑过渡曲面。
文中算法均在CAM5 曲面造型系统中进行开发,在叶片的光顺造型过程中,用户选择航空发动机叶片的数据点文件,系统读取数据点后,在用户操作下,自动进行叶片曲面光顺造型相关操作,包含诱导曲线的构造、弧长参数化方式光顺中弧线的获取、光顺叶片截面轮廓线生成、叶身曲面造型以及前后缘过渡曲面造型,直到完成叶片曲面光顺造型。
2 结果分析
2.1 理论分析
假设给出某条曲线的参数表达式C(u),a≤u≤b,其中,a∈R,b∈R,曲线上的数据点集为{pi},其中,i=0,1,…,n,则按照积累弦长参数化所得到的参数区间为

对于曲线C(u),弧长参数表示式为
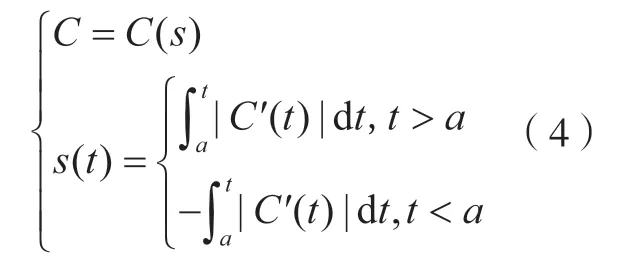
式中,s为弧长参数;a为曲线初始参数左边界;t为积分参数;s(t)为一个确定的极限,与曲线整体长度、数据点集分布、曲线局部的曲率变化率无关,因此其精度高于积累弦长参数化。本文的优化方法构造了弧长参数化的光顺中弧线以及叶身曲线,选择合适的曲面放样方法得到叶身曲面。在边缘过渡部分,由于曲线整体长度较短,且脊线参数分布合理 (为叶身曲面的边界),故采取积累弦长参数化方式,为尽量消除曲率变化率对精度的影响,在参数化时采取了加密的策略。数据点的参数经上述步骤完全确定,在4 张曲面上的数据点沿双方向等参数线曲率变化平滑,避免了曲面的扭曲现象,达到光顺的效果。
2.2 造型实例分析
为验证本文提出的叶片曲面光顺造型方法的正确性,选取具有20层截面轮廓线的某型号航空发动机叶片数据点为例,进行了叶片曲面光顺造型试验验证,叶片的加工最大允许误差为–0.03~+0.05 mm。通过对造型结果以及实际加工效果的分析,验证了所提出方法的正确性。结果分析从以下4 方面进行。
(1)精度分析。计算所有数据点到生成曲面的距离,为简洁起见,图12中仅展示叶背曲面的100 个数据点及后缘过渡曲面的100 个数据点。其中数据点到叶身曲面的最大距离为0.008915 mm,到前缘后缘过渡曲面最大距离为0.006173 mm,均满足叶片建模的精度要求。
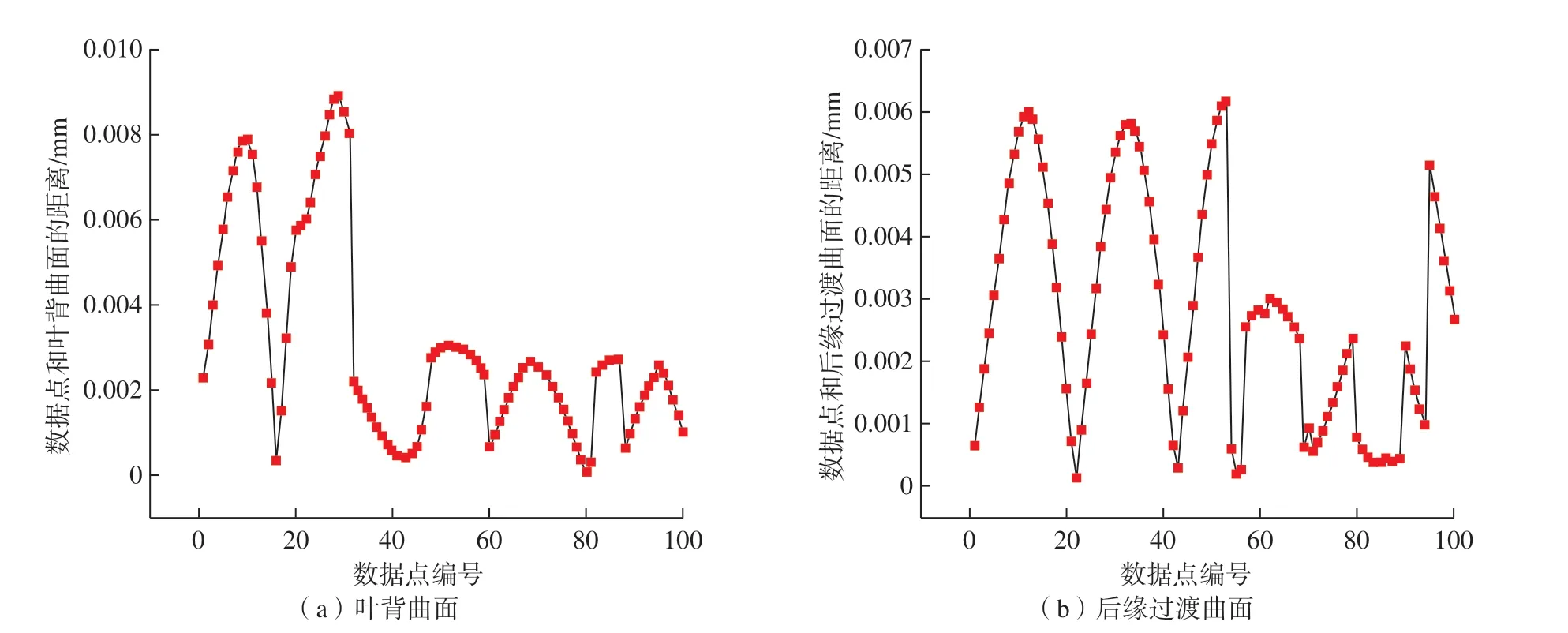
图12 数据点到曲面的距离Fig.12 Distance of data point to surface
(2)曲面曲率分析。分别对初始叶片曲面和经过手工调整的模型曲面以及利用文中算法生成的光顺叶片曲面进行曲率分析。图13中曲面由左至右分别是UG 初始建模曲面、人工调整的曲面和光顺造型曲面。从分析结果可以看出,UG 直接通过插值曲线和曲线组方式建模,将叶片模型作为一个整体来进行曲面建模,其在前缘和后缘部分有曲率突变并延伸到了叶身部分 (图13(b)),人工调整的模型曲面有同样的问题,而通过文中方法进行的叶片光顺曲面建模是由叶盆、叶背、前缘、后缘4个部分构成,通过精确的分区避免了曲率突变问题,较剧烈的曲率变化被严格地限制在边缘过渡曲面部分,在边缘和叶身过渡部分曲率变化更加平滑,曲面的整体也更加光顺。

图13 曲面的曲率分析Fig.13 Curvature analysis of surfaces
(3)截面轮廓线曲率梳分析。截面轮廓线的曲率梳分析最能说明曲线的光顺性,以曲率为参数对3 个模型均进行了相同参数位置的截面轮廓线曲率梳生成。初始模型的截面轮廓线在前后缘过渡部分保持了G1连续,但叶身曲线曲率变化不平滑;手工调整模型是根据加工经验,通过人工修改数据点使其符合加工要求,可以看到,其叶身曲率变化不平滑,且在前后缘过渡部分无法保证G1连续。虽然可以生成较为平滑的刀轨,但是对于曲面建模而言具有很大的风险与不确定性。通过分析对比 (图14)可以得到结论:应用文中算法进行快速建模的光顺叶片曲面模型,其截面轮廓线曲率变化平滑,且在前缘后缘部分保持G1连续,具有良好的几何性质。

图14 截面轮廓线曲率梳分析Fig.14 Curvature comb of profile curves
(4)刀轨平滑性分析。应用控制变量法,分别在3 个模型中生成的叶片曲面上相同区域选取相同的加工参数生成刀轨,在初始模型中生成的刀轨有回折,从而引起刀轴突变,因此试件加工后表面会有振纹,加工效果很差。而应用文中算法生成的叶片曲面上的刀轨平滑无回折,加工效果较好且满足加工要求,如图15和16 所示。由此可以得到结论:利用文中优化方法快速自动生成的光顺叶片曲面具有良好的参数均匀性及光顺度,减少了刀轨的波动性,从而大幅提高加工质量、减少机床磨损。
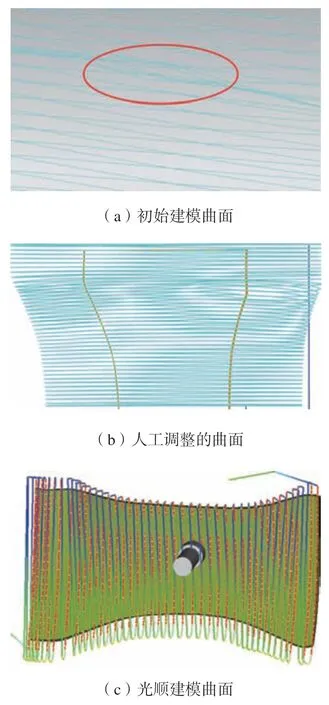
图15 刀具轨迹的生成Fig.15 Generation of toolpaths
3 结论

图16 经过加工的叶片Fig.16 Machined blade
(1)本文以航空发动机叶片为研究对象,对叶片曲面造型中存在的问题进行分析,将叶片特征之间的关系解耦与特征曲面均匀参数化相结合,提出了基于高参数均匀性的叶片曲面光顺造型方法。考虑到叶片目前的整体造型过程较为烦琐,将优化算法集合于曲面造型系统中,用户可以通过简易操作自动高效地获取光顺的叶片曲面。
(2)本文提出优化算法通过生成4 张曲面以代替整张封闭曲面,实现了对叶片造型过程的解耦,避免了叶片边缘过渡部分和叶身部分的过度约束,在使算法流程简化的同时保证了造型精度,利于在实际工程中的应用。
(3)在叶片造型过程中实现特征曲面双方向均匀参数化,有效提升了曲面的光顺程度,便于后续的加工。在叶片曲面上具有相同v参数的点可以构成等v参数线族,在实际加工中可以进一步研究此曲线族与加工方法的关系。文中提出的方法还可以推广至其他具有复杂曲面特征的典型航空类零件的曲面造型。
(4)在输入数据点后,用户只需要进行简单的操作即可应用优化算法快速自动地生成光顺叶片曲面,解决了叶片曲面造型整体流程烦琐的问题。将优化方法应用于某型号叶片的实际加工,数据分析和加工效果验证了方法的正确性。
