Design of a Computational Heuristic to Solve the Nonlinear Liénard Differential Model

Li Yan,Zulqurnain Sabir,Esin Ilhan,Muhammad Asif Zahoor Raja,Wei Gao and Haci Mehmet Baskonus

1School of Engineering,Honghe University,Mengzi,661199,China

2Department of Mathematics and Statistics,Hazara University,Mansehra,21300,Pakistan

3Faculty of Engineering and Architecture,Kirsehir Ahi Evran University,Kirsehir,40500,Turkey

4Future Technology Research Center,National Yunlin University of Science and Technology,Yunlin,64002,Taiwan

5School of Information Science and Technology,Yunnan Normal University,Kunming,650500,China

6Department of Mathematics and Science Education,Faculty of Education,Harran University,Sanliurfa,63500,Turkey

ABSTRACT In this study, the design of a computational heuristic based on the nonlinear Liénard model is presented using the efficiency of artificial neural networks (ANNs) along with the hybridization procedures of global and local search approaches.The global search genetic algorithm(GA)and local search sequential quadratic programming scheme(SQPS)are implemented to solve the nonlinear Liénard model.An objective function using the differential model and boundary conditions is designed and optimized by the hybrid computing strength of the GA-SQPS.The motivation of the ANN procedures along with GA-SQPS comes to present reliable,feasible and precise frameworks to tackle stiffand highly nonlinear differential models.The designed procedures of ANNs along with GA-SQPS are applied for three highly nonlinear differential models.The achieved numerical outcomes on multiple trials using the designed procedures are compared to authenticate the correctness,viability and efficacy.Moreover,statistical performances based on different measures are also provided to check the reliability of the ANN along with GASQPS.

KEYWORDS Nonlinear Liénard model; numerical computing; sequential quadratic programming scheme; genetic algorithm;statistical analysis;artificial neural networks

1 Introduction

In scientific fields, most of the real-world problems are observed in plasma physics, solid state physics, mathematical biology, fluid dynamics, and chemical kinetics, which have been stated in the form of differential systems[1].Various approaches have been exploited to solve these types of models,like Chebyshev polynomial based approximation scheme, closed-form scheme, spectral collocation method,subdomain finite element scheme,Bernoulli collocation method,predictor-corrector scheme,variational iteration scheme,homotopy perturbation scheme,differential quadrature scheme,quantic B-spline differential scheme, power series scheme, differential transformation scheme, Pade series scheme and Legendre polynomial function approximation and so on[2-7].

The present study is related to solving a nonlinear Liénard model (NLM) using the efficiency of artificial neural networks (ANNs) along with hybridization procedures of global search genetic algorithm (GA) and local search sequential quadratic programming scheme (SQPS). All the abovecited schemes have their own benefits and drawbacks, however, the stochastic computing efficiency based on ANN along with GA-SQPS is neither been tested nor implemented to solve the stiff-natured NLM.The NLM is mathematically given as[8]:

The above form of the NLM is used to generalize the damped springmass system as well as these models have been applied in the physically substantial areas by taking different values of theq(f),u(f)and.In the above NLM,u(f)is the restoring force,is the external force andq(f)f＇is the damping force.By takingq(f)=ε(f2-1),u(f)=fand= 0,the model form becomes the nonlinear Van der Pol model based on the electronic vacillation[9].The NLM is implemented in the modeling of fluid mechanics[10].Furthermore,the vacuum tube technology progressed by using oscillating circuits based on the NLM[11].

Due to the huge importance of the NLM,the focus of the research community was to present the significant applications of this model[12-19].The computing stochastic solvers are used to present the solutions of various singular models, functional differential systems, biological systems, prediction models and fractional applications [20-29]. However, the stochastic computing efficiency based on the strength of ANN along with GA-SQPS has not been implemented to present the numerical performances based on the NLM. These stochastic contributions proved the worth to observe the robustness and accuracy-based ANN along with GA-SQPS for solving the NDM.

Few novel influences based on the stochastic scheme are shortened as:

• Design of ANN along with GA-SQPS is presented successfully for solving the NLM.

• The matching of achieved and exact results for three different problems based on the NLM establish convergence,reliability and precision.

• The values of the absolute error(AE)are obtained in good measures for solving each example based on the NLM.

• The consistent,accurate performance is observed through statistical observations on multiple trials of ANN along with GA-SQPS in terms of semi-interquartile range(S.I.R),mean absolute deviation (MAD), Nash Sutcliffe Efficiency (NSE) and Theil’s Inequality Coefficient (TIC)metrics.

• Beside sensibly precise continuous input training interval, ease in the concept, robustness,smooth implementable training,extendibility and stability are other commendable proclamations for the designed ANN along with GA-SQPS.

The rest of the paper is organized as; Section 2 presents the designed procedure, optimization process and statistical performances.Section 3 describes the discussions of the results.Section 4 shows the conclusions and upcoming research directions.

2 Methodology

This section presents the design of the ANN along with GA-SQPS measures to solve the nonlinear Liénard differential model. The detail of fitness function is accessible using the mean square error along with the learning practice of the hybrid computing GA-SQPS.

2.1 Mathematical ANN Modeling

The ANNs have been exploited to solve various applications arising in numerous fields [30].The proposed results are signified aswhileis thenthderivative. The mathematical terminologies are given as:

whereksignifies the neurons,Lis the activation function and [aP,wP,bP] denote thepthcomponent form of[a,w,b].The log-sigmoid= 1/(1+activation function in the networks is written as:

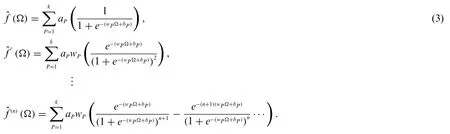
An error based fitness function(EFit)is given as:

HereEFit-iandEFit-iiare the fitness functions associated to NLM and its boundary conditions,given as:

whereNh= 1,fP=,q(f)=q(fP),U(f)=U(fP)andgP=gh.One may describe the Eq.(1)with the availability of suitable weightsW,i.e.,EFit→0.

2.2 Optimization Procedure:GA-SQPS

The optimization processes to solve the nonlinear Liénard differential model using the designed ANN along with GA-SQPS measures are provided in this section.

GA is an optimization based global search technique work to present the solutions of the linear and nonlinear networks. It is normally implemented to regulate the precise population results for numerous steep/complex systems based on the optimal training performance.GA is applied recently as automatic clustering [31], molecular sequence alignment, bioinformatics [32], energy efficiency and thermal comfort in building design [33], structural optimization [34], weight setting problem in OSPF/IS-IS routing[35],assembly sequences[36],image annotation[37],CNN template learning[38]and risk-based partner selection problem[39].

The performance based on the GA optimization converges rapidly by the hybridization with the local search scheme by taking its best values as initial inputs.Therefore,an efficient SQPS,i.e.,a local search technique is implemented in the process of hybridization.SQPS is used recently in unified fullchip CMP model aware dummy fill insertion framework [40], quasilinear parabolic optimal control problems[41],convex/nonconvex economic dispatch models[42],fractional order control design[43]and economic dispatch of micro-grid[44]and some related other applications[45-47].The designed structure using the ANN procedures along with GA-SQPS for the NLM is presented in Fig.1.

2.3 Performance Measures

The statistical operators performances of MAD, TIC, S.I.R and ENSE are provided together with the global representations to check the reliability of the designed ANN along with GA-SQPS.The detailed pseudocode based structure of the designed ANN along with GA-SQPS for solving the NLM is presented in Table 1.The mathematical notations of the statistical operators are written as:

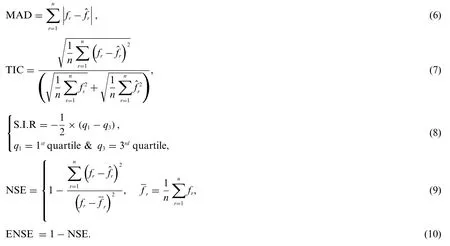
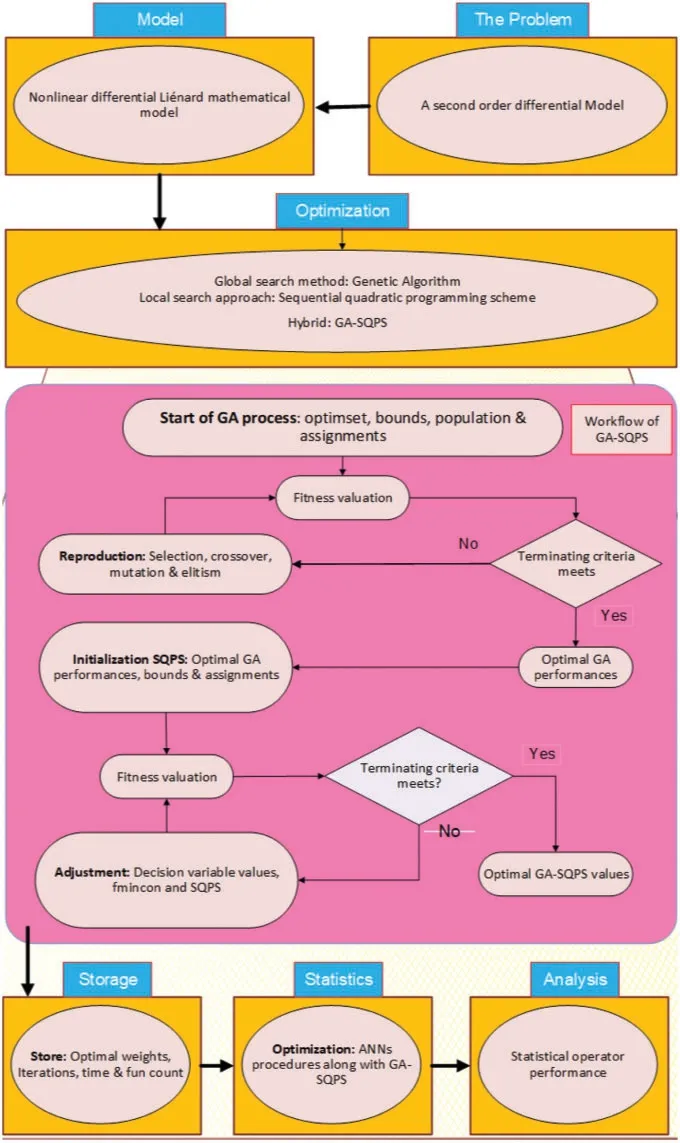
Figure 1:Designed structure using the ANN procedures along with GA-SQPS for the NLM

Table 1: Detailed structure of the designed ANN along with GA-SQPS for solving the NLM

3 Simulations and Results Performance

The current section present the result discussions for three different problems based NLM by applying the ANN along with GA-SQPS.The graphical and numerical measures have been provided to assess the convergence and accuracy.

Problem 1:Consider the NLM involving trigonometric ratios is given as[8]:

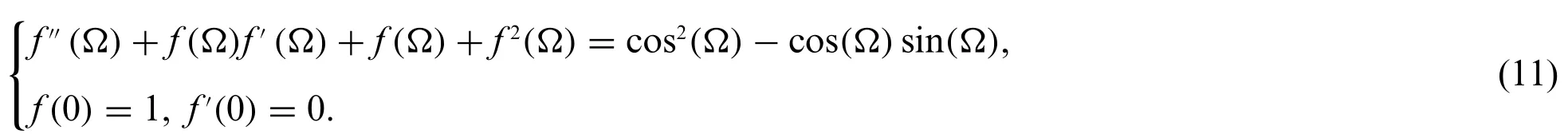
The exact form of the solution is cos,the error function is given as:

Problem 2:Suppose the higly NLM is written as[8]:

The exact solution of Eq.(13)isand the error function is given as:

Problem 3:Suppose the higly NLM is shown as[8]:

The exact solution of Eq.(13)isand the error function is given as:

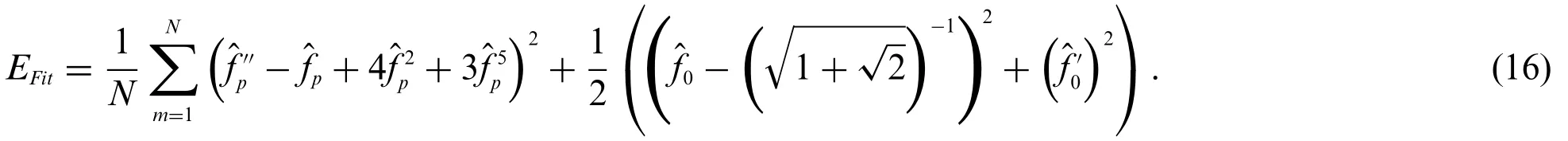
The results based on NLM for problems 1 to 3 have been performed through the numerical performance of global and local search GA-SQPS. These optimization procedures of GA-SQPS is provided in Table 1 and the whole practice is repeated for fifty multiple runs to produce a larger data of parameters.The proposed results through the designed ANN along with GA-SQPS are provided using the trained weights and mathematically given as:

The graphical measures are provided in Figs.2 to 6 for each problem based on a nonlinear Liénard differential model using 30 numbers of variable,10 neurons with[0,1]input and 0.05 step size.The obtained results based on best weights are given in Figs.2a-2c using the above Eqs.(17)-(19).The comparison plots based on the exact,best and mean solutions are accessible in Figs.2d-2f.The mean and best results are plotted using the proposed ANN along with GA-SQPS and presented with the true results. The matching of the proposed and true outcomes validates the correctness of the proposed ANN along with GA-SQPS.The AE plots based on the best and mean solutions are drawn in Subfigures 2g and 2h. It is observed that the AE best values for problems 1-3 lie 10-07to 10-10,10-05to 10-07and 10-06to 10-08, respectively. The mean AE values were found around 10-02-10-04,10-03-10-04and 10-02-10-03for problems 1,2 and 3.The performance procedures for the best,mean and worst results for the NLM is provided in Figs.2j-2l. For problem 1, the best MAD, TIC and ENSE operator values lie around 10-07to 10-10,10-10to 10-11and 10-13-10-15,the values based on the mean operators of MAD,TIC and ENSE lie as 10-03-10-05,10-06-10-08and 10-03-10-04,while the worst MAD, TIC and ENSE operators found as 10-01-10-02, 10-04-10-05and 10-02-10-03. For 2ndproblem,the best MAD, TIC and ENSE operators are calculated as 10-05-10-06, 10-08-10-09and 10-04-10-05,the MAD,TIC and ENSE operator mean values are 10-03-10-04,10-07-10-08and 10-02-10-04,while the MAD,TIC and ENSE worst operator measures found as 10-02-10-03,10-05-10-06and 10-03-10-04.For 3rdproblem,the best MAD,TIC and ENSE operators found as 10-05-10-06,10-09-10-10and 10-10-10-11,the MAD,TIC and ENSE mean operators are 10-03-10-04,10-06-10-08and 10-02-10-04,while the MAD,TIC and ENSE operator worst performances found as 10-01-10-02,10-03-10-05and 10-02-10-03.These best presentations through the comparison of the results in the form of AE along with the statistical operators indicate the correctness of the proposed scheme for the NLM.

The statistical representations for Fitness (FIT), TIC, MAD and ENSE together with the histograms are provided in Figs.3-6.The best FIT values are observed in Fig.3,which are reported as 10-07-10-09, 10-08-10-11and 10-04-10-08for 1-3 problems. Fig.4 shows the optimal TIC values calculated as 10-08to 10-11for problem 1 to 3.Fig.5 presents the optimal MAD performances,which are observed as 10-04to 10-08for 1 to 3 problem. Fig.6 illustrates the opimal ENSE performances,which are observed around 10-09-10-14for 1stproblem,10-07-10-08for 2ndproblem and 10-04to 10-07for 3rdproblem. In another sense, one can observe based on these performances that almost 85%of executions achieved a very reasonable and precise accuracy level of the statistical measures. The optimization tool built-in command MATLAB has been used in this study for the optimization procedure as well as other simulation studies.

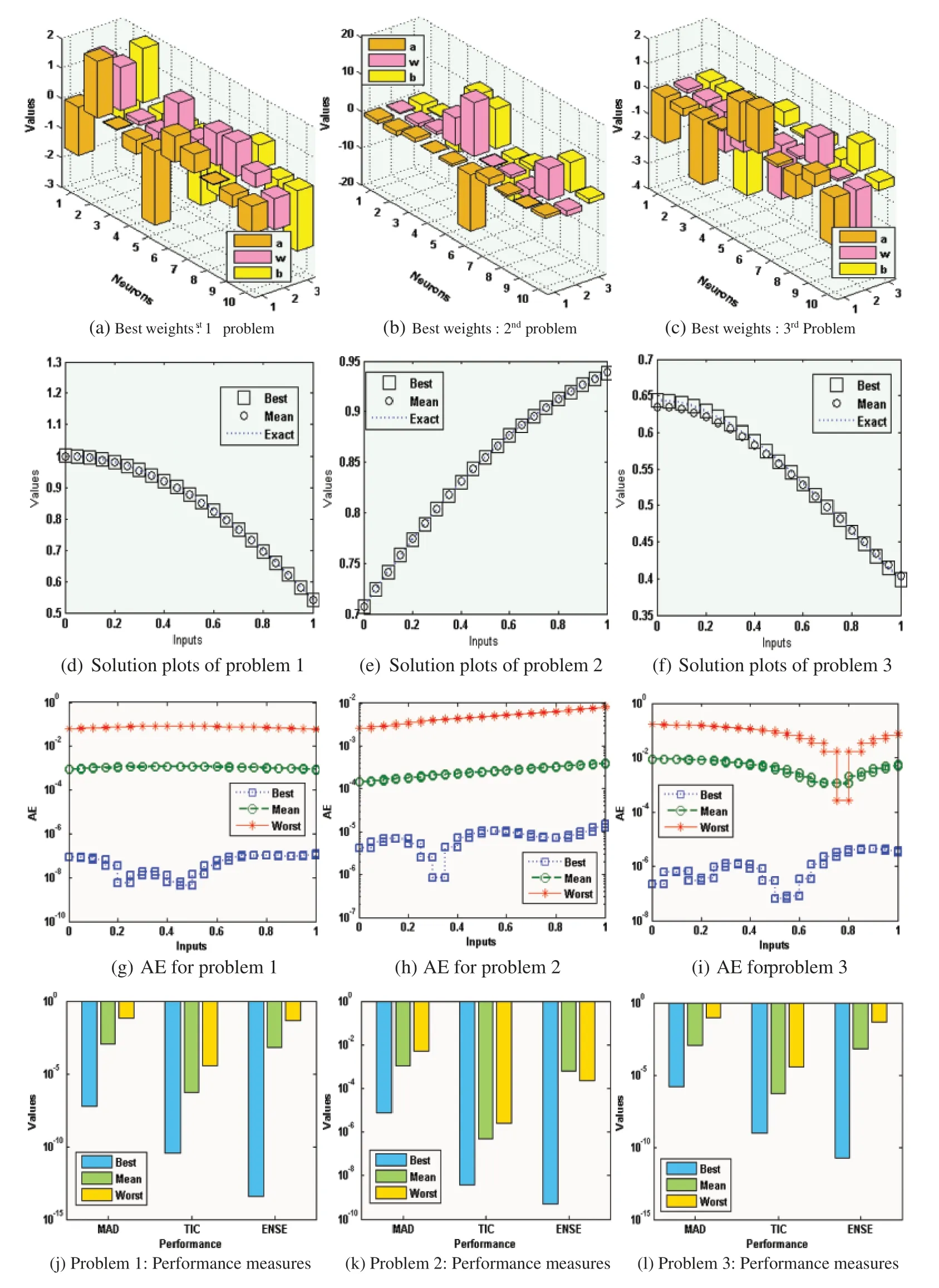
Figure 2:Best weights,solution plots,AE and performance indices for each problem of NLM

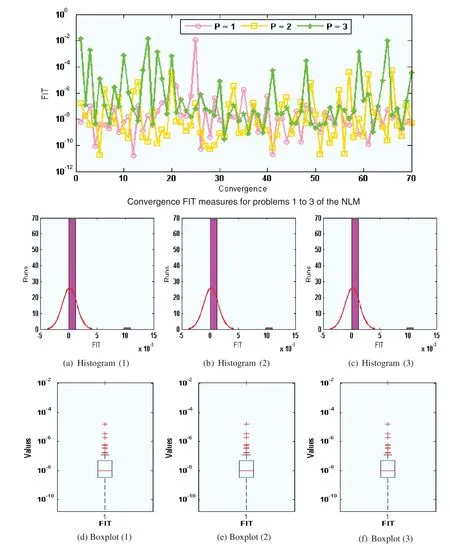
Figure 3:Performances of the FIT convergence for problems 1 to 3 based NLM

Figure 4:Performances of the TIC convergence for problems 1 to 3 based NLM

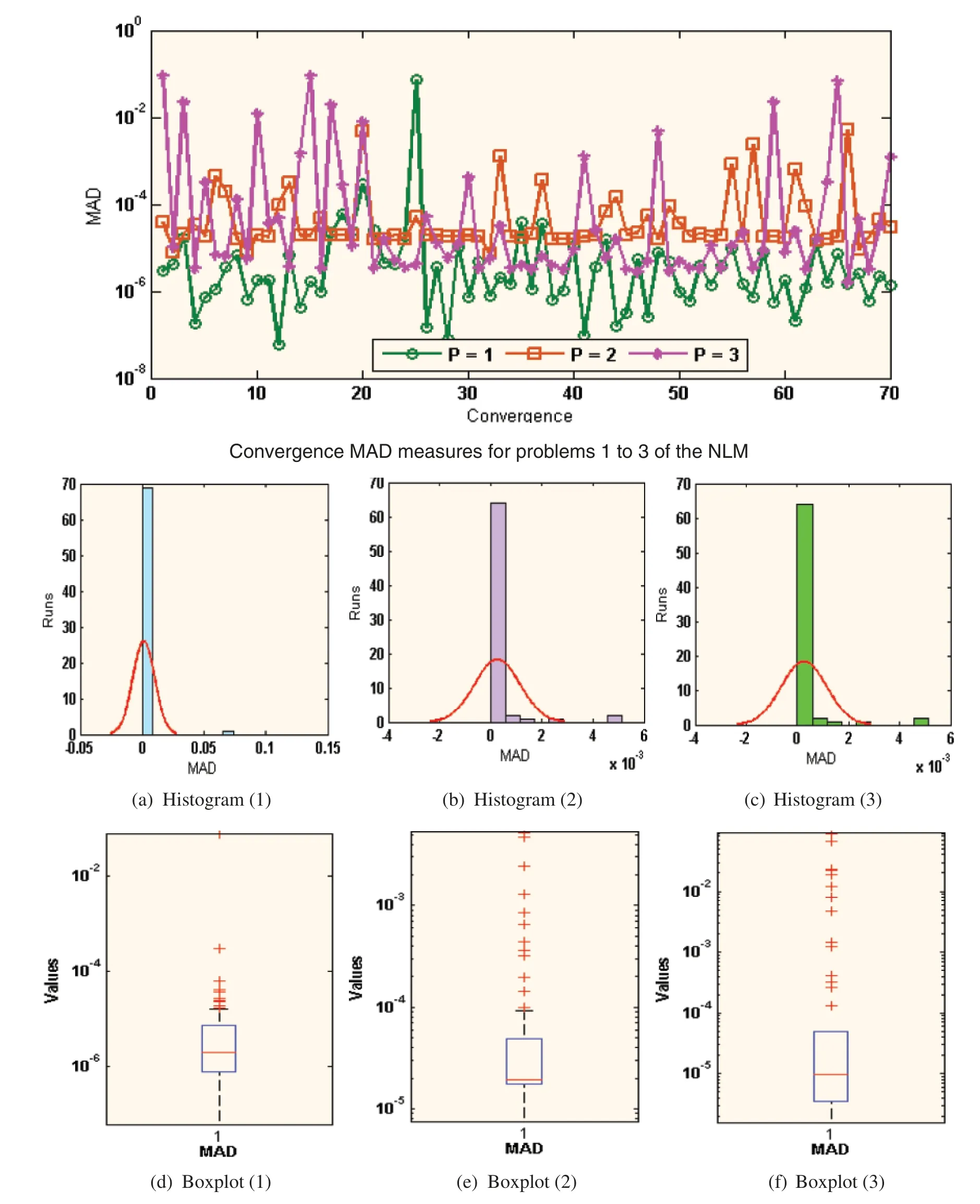
Figure 5:Performances of the MAD convergence for problems 1 to 3 based NLM

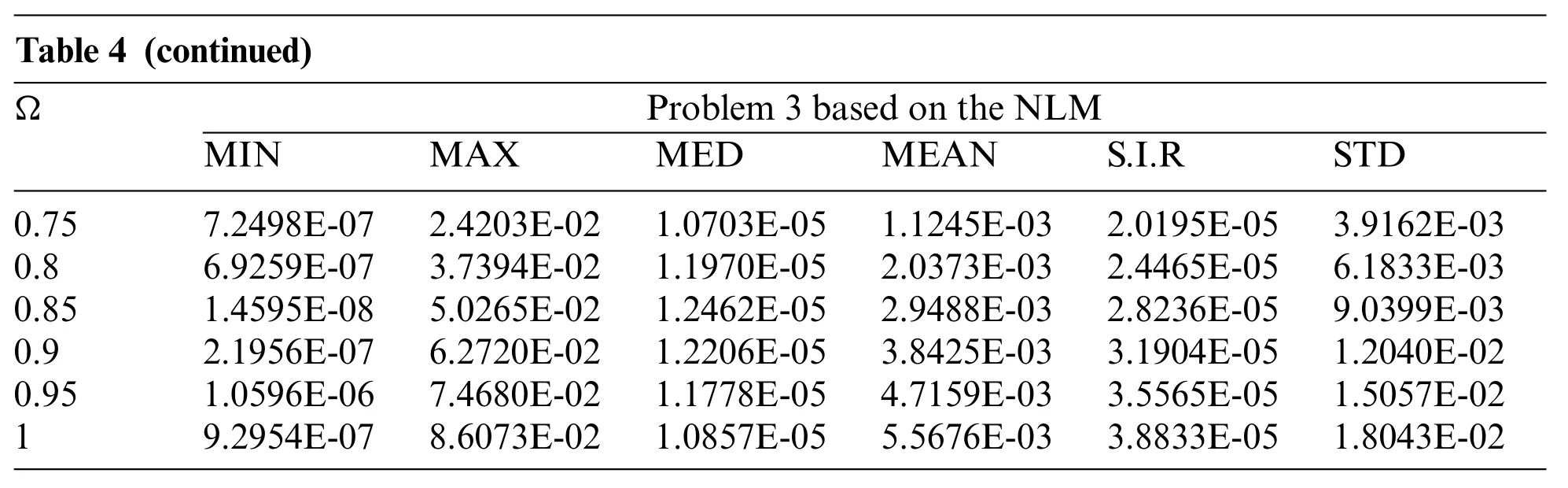
In order to observe the precision as well as accuracy level of the proposed ANN along with GASQPS, the statistical performances based on minimum (MIN), Maximum (MAX), median (MED),Mean,S.I.R and Standard deviation(STD)are considered for 50 independent executions in Tables 2-4 for each problem of the NLM.The MIN operator shows the ideal results,whereas MAX values shows the bad values and the S.I.R operator.The small dependable values of the MEAN,STD,MED,MIN,S.I.R and even MAX values for the NLM show the accuracy of the stochastic performances to solve the NLM.

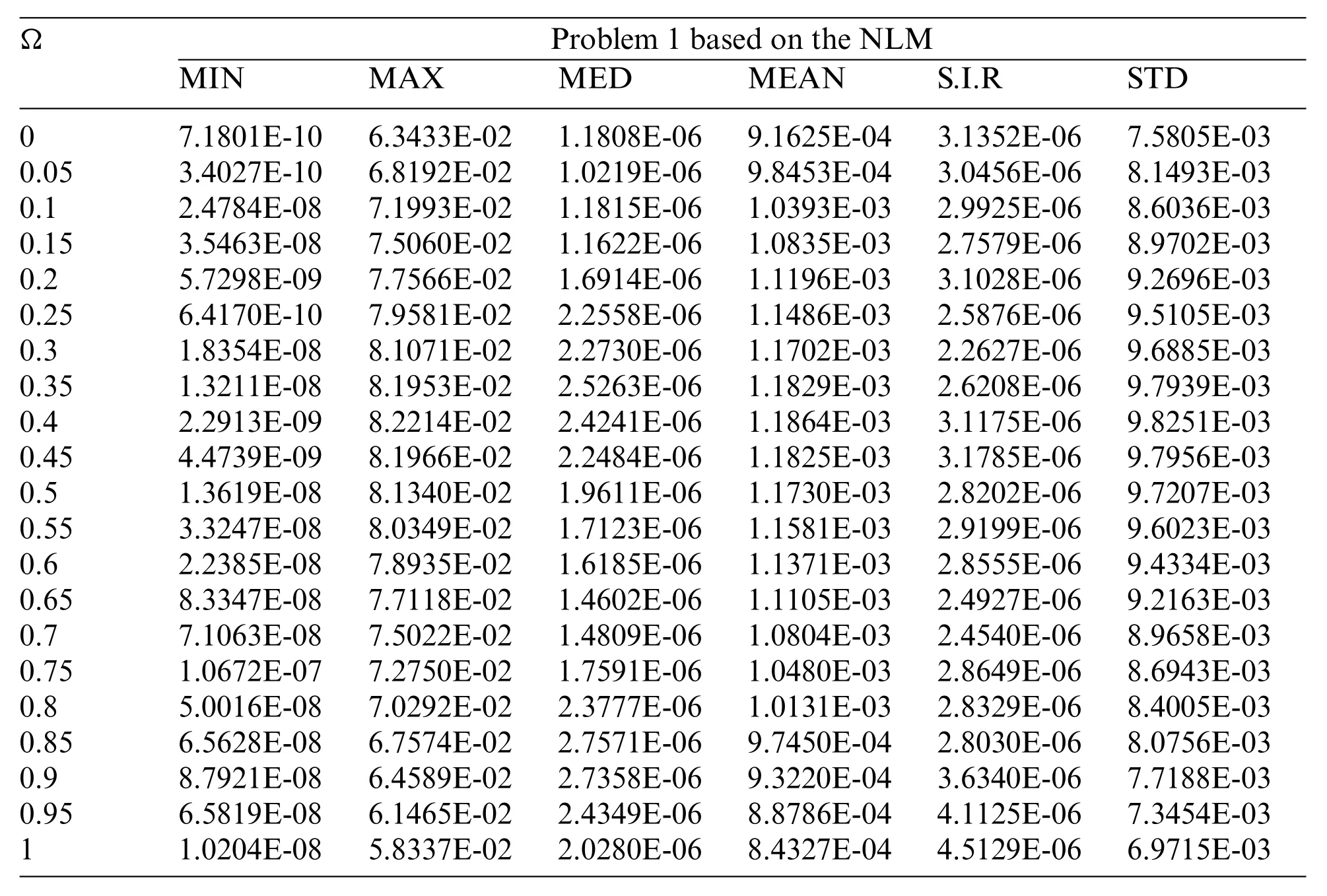
Table 2: Statistical measures of the proposed ANN along with GA-SQPS for the NLM based problem 1

Table 3: Statistical measures of the proposed ANN along with GA-SQPS for the NLM based problem 2

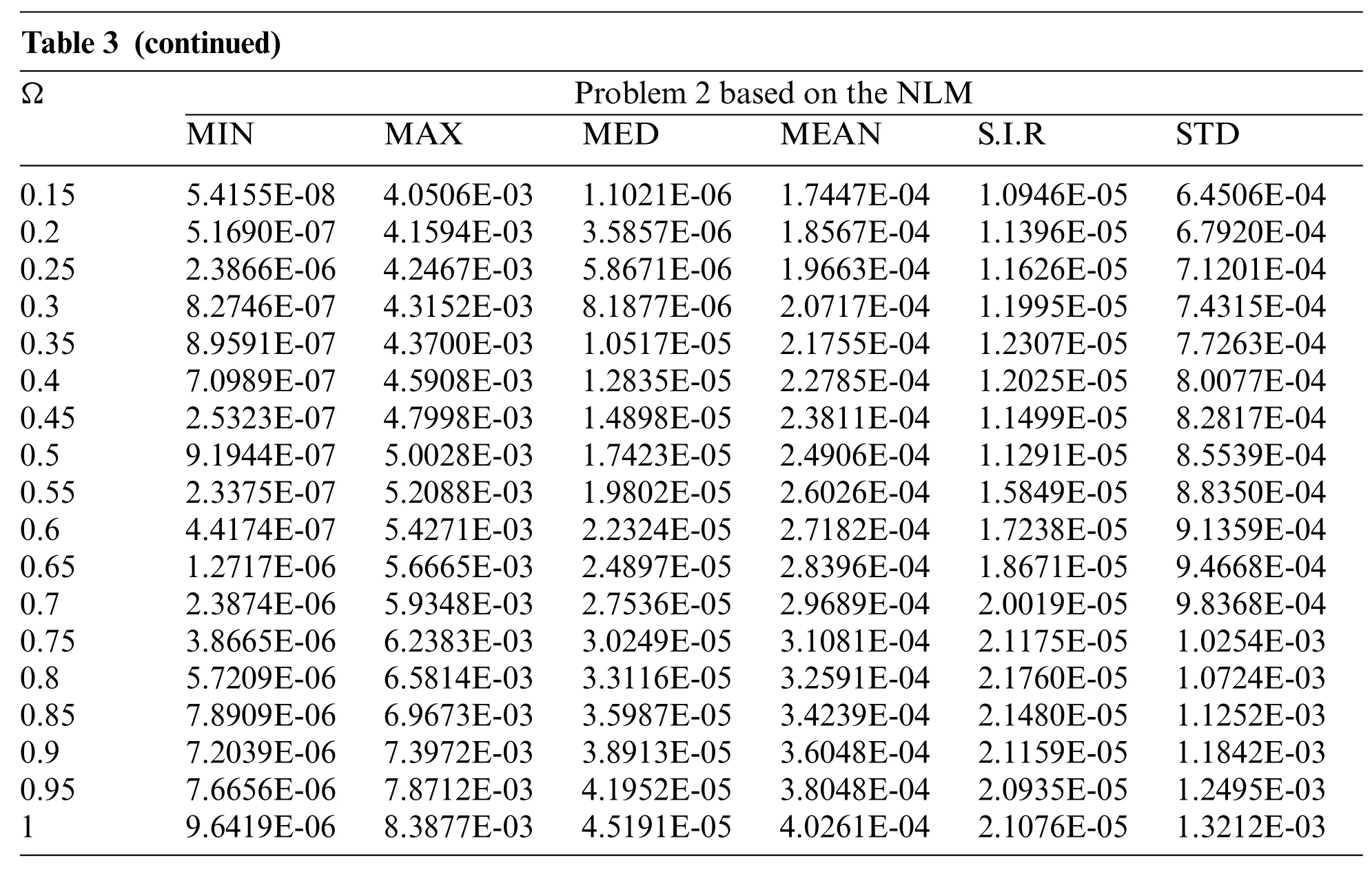
Table 3 (continued)Problem 2 based on the NLM MIN MAX MED MEAN S.I.R STD 0.15 5.4155E-08 4.0506E-03 1.1021E-06 1.7447E-04 1.0946E-05 6.4506E-04 0.2 5.1690E-07 4.1594E-03 3.5857E-06 1.8567E-04 1.1396E-05 6.7920E-04 0.25 2.3866E-06 4.2467E-03 5.8671E-06 1.9663E-04 1.1626E-05 7.1201E-04 0.3 8.2746E-07 4.3152E-03 8.1877E-06 2.0717E-04 1.1995E-05 7.4315E-04 0.35 8.9591E-07 4.3700E-03 1.0517E-05 2.1755E-04 1.2307E-05 7.7263E-04 0.4 7.0989E-07 4.5908E-03 1.2835E-05 2.2785E-04 1.2025E-05 8.0077E-04 0.45 2.5323E-07 4.7998E-03 1.4898E-05 2.3811E-04 1.1499E-05 8.2817E-04 0.5 9.1944E-07 5.0028E-03 1.7423E-05 2.4906E-04 1.1291E-05 8.5539E-04 0.55 2.3375E-07 5.2088E-03 1.9802E-05 2.6026E-04 1.5849E-05 8.8350E-04 0.6 4.4174E-07 5.4271E-03 2.2324E-05 2.7182E-04 1.7238E-05 9.1359E-04 0.65 1.2717E-06 5.6665E-03 2.4897E-05 2.8396E-04 1.8671E-05 9.4668E-04 0.7 2.3874E-06 5.9348E-03 2.7536E-05 2.9689E-04 2.0019E-05 9.8368E-04 0.75 3.8665E-06 6.2383E-03 3.0249E-05 3.1081E-04 2.1175E-05 1.0254E-03 0.8 5.7209E-06 6.5814E-03 3.3116E-05 3.2591E-04 2.1760E-05 1.0724E-03 0.85 7.8909E-06 6.9673E-03 3.5987E-05 3.4239E-04 2.1480E-05 1.1252E-03 0.9 7.2039E-06 7.3972E-03 3.8913E-05 3.6048E-04 2.1159E-05 1.1842E-03 0.95 7.6656E-06 7.8712E-03 4.1952E-05 3.8048E-04 2.0935E-05 1.2495E-03 1 9.6419E-06 8.3877E-03 4.5191E-05 4.0261E-04 2.1076E-05 1.3212E-03

Table 4: Statistical measures of the proposed ANN along with GA-SQPS for the NLM based problem 3

?

The convergence measure performances are further accompanied based on the global operators of FIT, TIC, MAD and ENSE for fifty executions given in Table 5. For problems 1 to 3 based on the NLM, the MIN performances of these operators lie as 10-04-10-06, 10-03-10-04, 10-06-10-07and 10-03-10-06. The S.I.R performances of these operators found as 10-03-10-06, 10-02-10-04, 10-06-10-07and 10-03-10-05. These performances based global operators confirm the exactness of the designed scheme.

Table 5: Global operator performances for each problem of the NLM

The computational cost of the proposed ANN along with GA-SQPS is inspected through the parameter variation of the typical time,completed cycles/iterations and executed function count.The complexity investigations of each problem of the NLM based on the numerical measures are provided in Table 6.One can find that the average generations,executed time and function assessment lie around 113.2780, 204.7667 and 13914.3238 for each problem of the NLM. These numerical measures are provided to associate the efficiency of the ANN along with GA-SQPS.

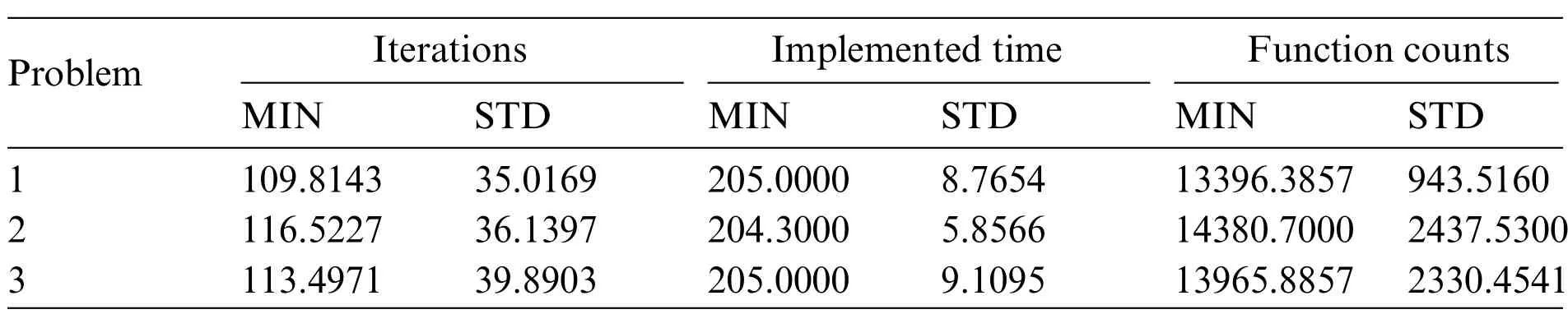
Table 6: Complexity performances for the NLM

4 Conclusion

The present work is related to solving the nonlinear Liénard model numerically through the computational intelligent ANN procedures and GA-SQPS.The nonlinear Liénard differential model is observed in the generalization of a damped spring mass and the Van der Pol system.The nonlinear Liénard equations are implemented in the modeling of fluid dynamics,vacuum tube technology/radio and oscillating circuits. The optimization of the objective function has been performed through the approximation capability of ANN along with GA-SQPS.The proposed ANN along with GA-SQPS is applied for three problems based on the NLM.The correctness of the scheme is observed by comparing the proposed results with the exact solutions. The detail of the AE, performance measures through different indices, convergent plots and weight vectors have also been provided. The accurate and specific presentations of the scheme are observed as 6 to 8 decimal places of accuracy level from the exact obtainable solutions for each example of NDM. The statistical presentations of MIN, MED,MAX, S.I.R, MEAN and STD measures certify the convergence of the designed scheme for the numerical treatment of the nonlinear Liénard differential model.

In upcoming work, the NLM can be numerically treated by using the swarming optimizations scheme based on the hidden layers of the Meyer and Morlet wavelet neural networks.Moreover,these procedures can be used to solve various nonlinear and fractional order models[48-65].

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.