融合降雨随机变量的洪水频率分布估计方法研究

江 聪，熊立华，黄俊哲，杨胜梅

(1.中国地质大学(武汉) 环境学院，湖北 武汉 430074；2.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；3.长江水利委员会长江科学院，湖北 武汉 430010)

1 研究背景

洪水频率分析是水利工程规划、设计、运行以及洪水风险评估的基础性工作[1-2]。传统的洪水频率分布估计方法一般假设洪水序列服从某一给定的理论分布(例如我国水文设计规范推荐皮尔逊Ⅲ型(PⅢ)分布[1-3])，然后由理论分布直接拟合实测样本并估计出相应的分布参数。洪水样本序列能否充分反映洪水事件发生的统计规律很大程度上决定了洪水频率分析成果可靠性[1]。然而，我国众多中小流域的水文站点设站时间普遍较晚，积累的水文资料有限，难以获取较长的洪水观测样本，导致洪水序列的代表性较差，影响了洪水频率分布估计的精度。因此，在洪水频率分析计算中，充分吸收和利用各种有助于洪水频率分布估计的有效信息，对提高水文设计成果的可靠性具有重要的意义。

在实测洪水样本有限的情况下，增加洪水样本信息量的主要途径包括引入历史调查洪水、插补延长洪水序列以及区域洪水频率方法。通过研究古洪水或者考证历史文献获取历史调查洪水能够大大延长洪水的追溯期，进而提高洪水样本的代表性，这也是工程水文设计中最常用的方法[1-3]。插补延长法通过建立洪水序列与某些参证变量的(如上下游相邻水文站的资料、相同水文站的其他水文要素等)的函数关系，插补或延长洪水序列，从而增加样本容量[2]。区域洪水频率方法能够引入相邻区域多个站点的洪水样本信息，基于水文相似性原理，建立区域洪水统计参数与流域一些特征变量的函数关系，该方法可以克服单站洪水样本量较为有限的缺点，有助于减小洪水频率分布估计的不确定性，并且可用于推求无资料站点的洪水频率分布[4-7]。需要指出的是，历史调查洪水的获取需要大量的考证工作，且历史洪水量级的估算也存在较大不确定性；插补延长洪水序列需要相关性较高的参证变量，同时还需要参证站具有较长的观测期，在资料缺乏的地区上述条件较难同时满足；区域洪水频率分析方法较为复杂，所需的资料繁多，目前主要以理论研究为主。

除了历史洪水样本或区域洪水样本信息外，一些与洪水具有物理或统计相关的变量(如降雨、大气环流指数等)也可以用于估计洪水频率分布[8-11]。大部分流域的洪水由暴雨形成，洪水与降雨之间往往存在显著的相关性[12]，国内外一些研究将降雨变量作为洪水频率分布参数的协变量，基于广义回归模型构建随降雨变化的洪水频率分布[9-11]。以上研究通常将降雨变量默认为一种确定性的变量，然而降雨本身作为一种自然现象，其量级大小必然具有一定的随机性，得到的洪水频率分布会随降雨的剧烈变化而剧烈变化，这种剧烈变化可能与实际情况并不相符。因此，在洪水频率分析中将降雨变量处理成确定性变量并不能合理反映洪水频率分布的变化规律。

本文基于层次模型构建一种融合降雨随机变量的洪水频率分布推导方法，将与洪水相关的降雨变量定义为随机变量，并估计相应的频率分布描述其发生规律，然后基于广义回归模型构建洪水对降雨变量的条件概率分布，最后由全概率公式推导出洪水频率分布。选取浙江省兰江流域兰溪水文站的年最大洪峰流量作为研究实例，引入年最大15天前期影响雨量作为洪峰流量的相依性变量，由层次模型推导该流域洪水频率分布，并进一步探讨引入降雨随机变量对提高洪水频率分布估计精度的意义。

2 融合降雨随机变量的洪水频率分布推导法

2.1 层次模型定义本研究基于层次模型，提出了一种融合降雨随机变量的洪水频率分布推导方法。定义某流域洪水变量为Y，其相依性降雨变量(如年降雨极值变量、不同时段的降雨量、雨强、暴雨笼罩面积等)定义为X，由一个条件概率分布表示Y与X的相关关系，即：

P(Y≤y|X=x)=FY|X(y|x)

(1)

式中FY|X(y|x)为Y在X=x条件下的概率函数，其密度函数fY|X(y|x)表达为：

(2)

式中：f(x，y)为洪水变量Y和降雨变量X的联合概率密度函数；fX(x)为X的概率密度函数。将式(2)写为：

f(x，y)=fX(x)·fY|X(y|x)

(3)

根据全概率公式[13]，洪水变量Y的概率密度函数fY(y)有如下表达式：

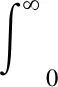
(4)

由上式可知，除了直接由某一假定的理论频率分布直接拟合洪水样本序列之外，洪水变量Y的频率分布还可以由降雨变量X的概率分布fX(x)与条件分布fY|X(y|x)推导得到。根据式(4)，洪水变量Y的频率分布可以表示为一个两阶段层次模型，即：

(5)

式中Y|X为Y对X的条件分布。

本研究采用PⅢ分布表示降雨变量X的频率分布，为了便于表示分布的统计特征值，PⅢ分布的概率密度函数写成如下形式：

(6)

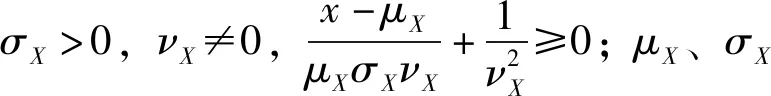
2.2 条件分布构建采用基于正态分布的广义回归模型刻画洪水变量Y与降雨变量X的关系，即：

(7)

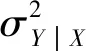
(8)

式中α0、α1、β0和β1分别为广义回归模型的参数，由极大似然法估计得到[14]。μY|X和σY|X的具体表达式根据贝叶斯信息准则(BIC)[15]从线性、指数和对数方程中优选。由上可以看出，在广义回归模型中，条件分布的位置参数μY|X刻画了洪水变量Y条件期望值与降雨变量X的关系，尺度参数σY|X刻画了随机误差项εY|X的分布，即实测洪水值y在其期望值μY|X附近的离散情况，表征了降雨变量X之外的随机因素(如降雨空间分布、雨强、蒸发等因素)对洪水变量Y的影响。此外，尺度参数σY|X间接反映了Y与X之间的相关性，具体来说，σY|X越大说明洪水变量与降雨变量之间的相关性越弱。

2.3 洪水频率分布计算与拟合优度分析理论上洪水变量Y的累积概率函数可由式(4)推求得到，即：

(9)

(10)

采用Kolmogorov-Smirnov(KS)方法[16]检验洪水频率分布拟合优度，如果检验统计量对应的p值大于某一阈值，则表明频率分布可以通过拟合优度检验，本研究中KS检验p值的阈值取0.05。为定量评估洪水频率分布拟合偏差大小，计算理论频率和经验频率值的均方根误差RMSE，具体表达式如下：

(11)

式中：m为实测洪水样本容量；rank(yi)为实测洪水样本yi在总体样本中的从小到大的序号。

3 实例研究

3.1 研究区域与数据选取位于浙江省的兰江流域作为研究区域，兰江是钱塘江上游面积最大的支流，发源于浙、皖、赣交界的莲花尖，东行经开化、常山、衢县、龙游、兰溪，在梅城与新安江汇合入富春江，其流域面积为19 240 km2，河长为304 km。兰江流域属亚热带季风气候，多年平均降雨量达到了1600 mm，雨量多集中在3—9月，占超过七成全年降雨量，洪水主要由锋面雨或台风雨形成，最大洪水多出现在6月份。

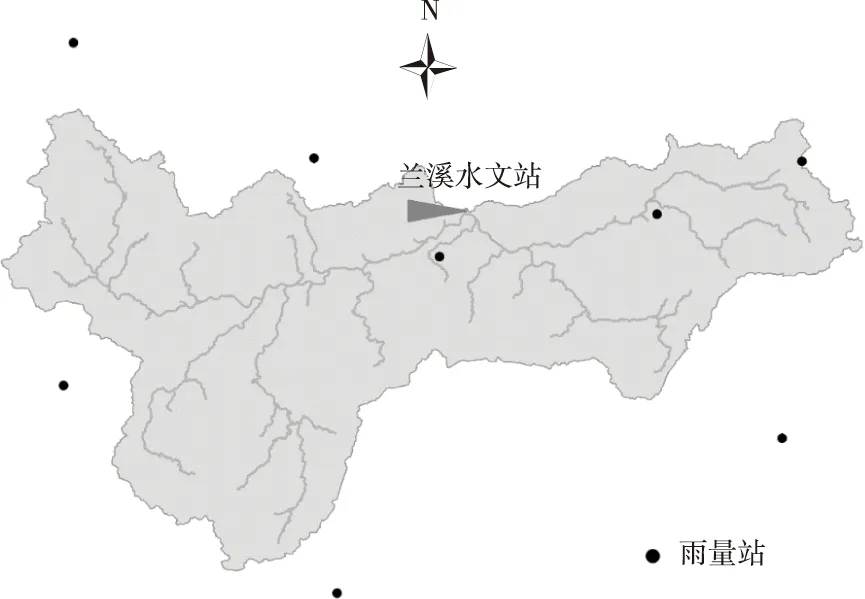
图1 兰江流域

兰溪水文站是兰江流域的控制性站点，集水面积为 18 230 km2，约占全流域面积的95%。本研究收集了兰溪站1953—2020年间的年最大洪峰流量序列，同时收集了兰江流域内和周边8个国家基准气象站的逐日降雨资料，并通过泰森多边形法进行插值得到整个流域逐日面雨量。经过分析，时间长度为15 d折减系数为0.91的年最大前期影响雨量与年最大洪峰流量的相关性最好，皮尔逊相关系数达到了0.845，显著性水平为0.01。年最大前期影响雨量综合了年极值雨量以及流域的前期蓄水量，且采用年极大值取样，不依赖场次洪水的信息，便于从实测的降雨序列计算得到，因此选取该变量作为年最大洪峰流量的相依性降雨随机变量。

3.2 融合降雨随机变量的洪水频率分布推导在层次模型框架下，首先估计年最大15 d前期影响雨量的频率分布及洪峰流量对前期影响雨量的条件分布。年最大15 d前期影响雨量的频率分布估计结果如表1与图2所示，总体而言，PⅢ分布对前期影响雨量序列有较合理的拟合效果，且能够通过显著性水平为0.05的KS检验。

表1 兰江流域年最大15 d前期影响雨量与年最大洪峰流量频率分布估计结果

图2 兰江流域年最大15 d前期影响雨量频率曲线

根据广义回归模型的估计结果，兰溪站年最大洪峰流量对年最大15 d前期影响雨量的条件分布参数有如下表达式：

(12)

根据以上结果可知年最大洪峰流量条件分布的位置参数μY|X(即条件期望值)与尺度参数σY|X(即均方差)均为年最大15 d前期影响雨量的对数函数。从图3看出，基于正态分布的广义回归模型能够较好地刻画洪峰流量对前期影响雨量的相依关系，实测点据较为均匀地分布在条件期望值的两侧。此外，图3还给出了不同典型前期影响雨量条件下，洪峰流量条件分布的概率密度曲线，可以看出洪水变量的条件期望值与实测值的离散程度也会随着前期影响雨量增加而变大。

图3 兰溪站年最大洪峰流量对年最大15 d前期影响雨量条件分布

在估计年最大15 d前期影响雨量频率分布以及洪峰流量条件概率分布的基础上，由层次模型推导出兰溪站年最大洪峰流量频率分布。KS检验的结果表明，融合降雨变量的洪水频率分布通过了显著性水平为0.05的拟合优度检验(见表1)，相应的频率曲线对大部分实测点据也有较好的拟合效果(如图4所示)。

图4 兰溪站年最大洪峰流量频率曲线

为了与传统的洪水频率分布估计方法相对比，采用PⅢ分布直接拟合实测洪水样本，由极大似然估计分布参数，具体参数估计结果如表1所示。KS检验结果表明，PⅢ分布对实测洪水序列同样具有较好的拟合效果。表1对比了融合降雨随机变量的洪水频率分布和PⅢ分布统计参数的差异，总体而言，两者得到的分布参数差别不大，PⅢ分布的均值、Cv和Cs值略大于前者的参数值。兰溪站年最大洪峰流量频率分布的PP图如图5所示，可以看出融合降雨随机变量的洪水频率分布整体拟合效果略优于PⅢ分布，前者的RMSE值为0.030，小于后者的RMSE值(0.037)。另一方面，PⅢ分布频率曲线的上尾部分对最大实测洪水值的拟合效果更好(如图4所示)。

图5 兰溪站年最大洪峰流量频率分布PP图

3.3 抽样统计实验分析通过前文分析可知，在前期影响雨量样本容量与洪水样本容量相同的条件下，由层次模型推导的融合降雨随机变量的洪水频率分布一定程度上减小了频率曲线的整体拟合偏差，但由于降雨序列并未延长洪水频率分布估计信息的追溯期，可能并不能有效提高洪水频率分布的估计精度。下面将重点探讨在降雨观测期长于洪水观测期的情况下，引入长系列降雨随机变量对减小洪水频率分布估计抽样误差以及提高水文设计成果可靠性的意义。

采用随机抽样方法，从68年的总体洪水样本中抽取一定长度的子样本序列，然后由子样本序列构建洪水对相应降雨变量的条件概率分布，最后结合前期影响雨量总体样本的频率分布(参数估计结果如表1所示)由层次模型推导出洪水频率分布。与之对比，采用PⅢ分布直接拟合洪水子样本序列，并由极大似然法估计出相应的分布参数。此外，基于线性回归方法建立洪水变量和前期影响雨量的函数关系，然后通过前期影响雨量总体样本序列对洪水序列进行插补延长，最后由PⅢ分布拟合插补延长后的洪水序列进而估计相应的频率分布。为分析洪水样本序列长度对洪水频率分布估计结果的影响，抽样长度分别设为20、30、40、50、60以及65，针对不同的抽样长度，分别重复上述统计实验1000次。

图6给出了由不同长度子样本序列估计得到的洪水频率分布对总体样本的拟合偏差。可以看出随着样本长度增加，由子样本估计得到的频率分布参数逐渐逼近整体样本的参数估计结果，频率分布的RMSE值也随之减小，以上结果表明无论是基于PⅢ分布的洪水频率分布估计方法还是本文提出的层次模型，样本序列长度都是决定洪水频率分布估计精度的重要因素。与直接由PⅢ分布拟合实测洪水样本的方法相比，插补延长法以及本文提出的层次模型都融合了长系列降雨信息，可以在不同程度上改进洪水频率分布的拟合效果，从图6(d)可以看出，后两种方法的整体拟合偏差(RMSE值)要明显更小。图6(a)—(c)可见，插补延长法可以明显提高洪水频率分布均值的估计效果，但对高阶参数的估计存在明显偏差，在子样本序列较短的情况下会显著低估Cv值和Cs值，这是由于插补延长法以线性回归模型的期望值作为插补延长值，忽略了模型的随机误差项。相比之下，本文构建的层次模型一方面充分利用了长系列降水信息，同时还通过广义回归模型误差隐含地考虑了其他随机因素对洪水频率分布的影响，其得到的洪水频率分布参数基本落在由总体样本序列估计得到的分布参数附近，没有明显的系统性偏差，因此结果更加合理；此外，模型的RMSE值整体上也要明显小于插补延长法的RMSE值。

图6 基于子样本序列洪水频率分布的估计偏差

根据随机抽样洪水序列的频率分布估计结果，图7给出了相应水文设计值的90%不确定性区间。与图6结果相对应，随着洪水样本量的增加，抽样误差对水文设计值的影响也逐渐减小，另外一方面，随着设计标准提高(即洪水超过概率减小)，抽样误差所带来的水文设计值不确定性也越来越大。插补延长法与层次模型由于引入了更长的降雨信息，可以显著减小抽样误差所带来的水文设计值不确定性。如图7(a)所示，在子样本序列长度为20的情况下，直接由PⅢ分布拟合实测洪水序列推求得到的千年一遇(即0.1%超过概率)水文设计值的90%不确定性区间宽度超过了26 000 m3/s，而其他两种方法相应的水文设计值不确定性区间宽度不到10 000 m3/s。同时也可以发现，插补延长序列虽然能减小水文设计值的不确定性，但由于低估了Cv值，导致水文设计值上尾部分的90%不确定性区间整体落在基于总体实测样本序列的频率曲线下方，水文设计值明显偏小。相比之下，由层次模型推求得到的水文设计值的90%不确定性区间较为均匀地落在基于总体洪水样本序列的频率曲线两侧，没有明显的系统性偏差，结果较延长插补法的结果更为合理。

图7 基于不同抽样长度水文设计值的90%不确定性区间

在整个洪水实测期内，兰溪站年最大洪峰流量出现在1955年，观测值为19 500 m3/s，明显高于其他年份的洪峰流量值。为分析最大洪水样本缺失对水文设计成果的影响，图8给出了剔除最大实测洪水样本的洪水频率曲线。从中可以看出基于实测洪水样本的PⅢ分布估计结果对最大洪水样本的缺失非常敏感，频率曲线的上尾部分与基于总体洪水样本的频率曲线相比明显向下偏离，得到的千年一遇水文设计值减小了将近5000 m3/s。插补延长方法一定程度可以减小样本缺失对洪水频率分布估计结果的影响，但推求得到的千年一遇设计洪水值仍然较基于总体样本的设计值减小了约2500 m3/s。而最大实测洪水样本的缺失对层次模型推求的水文设计值影响不大，从图8可以看出，基于总体样本的洪水频率曲线与剔除最大洪水样本的洪水频率曲线几乎重合，只有上尾部分略有偏离。以上对比结果表明，通过层次模型引入长系列降雨信息能够减小个别样本缺失对洪水频率分布估计结果的影响，使水文设计结果更加稳健。

图8 剔除最大洪水样本的水文设计值

4 结论与展望

本文在层次模型的框架下，提出了一种融合降雨随机变量的洪水频率分布推导方法，并将该方法应用于推求兰江流域年最大洪峰流量的频率分布，并且进一步探讨了该方法对提高洪水频率分析成果可靠性的意义。主要结论为：采用基于正态分布的广义回归模型构建了兰江流域年最大洪峰流量对年最大15天前期影响雨量条件概率，结果表明洪水条件概率分布的均值和均方差与前期影响雨量存在函数关系。在洪水序列和降雨序列样本容量相同的条件下，由层次模型推导的融合降雨随机变量的洪水频率分布与直接拟合实测洪水样本得到的PⅢ分布都能通过拟合优度检验，前者的拟合效果略好于后者。

通过抽样统计实验分析，在前期影响雨量序列样本长于实测洪水样本的条件下，基于层次模型推求的洪水频率分布充分利用了长系列降水信息，同时还通过广义模型误差隐含地考虑了其他随机因素对洪水频率分布的影响，相较于直接由PⅢ分布拟合实测洪水样本的方法以及插补延长法，本文提出的方法一定程度上可以提高洪水频率分布的估计精度，减小抽样误差导致的水文设计值不确定性。

在我国，气象站的设立时间通常要早于水文测站，气象资料的连续性与可靠性一般也要好于水文资料且更加容易获取，因此，本文提出的融合降雨随机变量的洪水频率分布推导方法为解决水文观测资料匮乏区域的水文设计问题提供了一种可行途径。另外，本文提出的方法还适用于推求未来降雨发生变化条件下的洪水频率分布，例如可根据观测数据建立洪水对降雨的条件分布，然后通过气候模式预测未来不同情景下的降雨数据并推求相应的降雨变量频率分布，最后将降雨频率分布代入层次模型即可推导出未来情景下的洪水频率分布。