岩体工程力学参数取值方法研究Ⅰ:原位试验与定量类比
2023-02-16汪小刚
汪小刚
(流域水循环模拟与调控国家重点实验室,中国水利水电科学研究院,北京 100038)
1 研究背景
合理确定岩体工程力学参数是岩土工程中开展其它一切工作的前提和基础,直接关系到工程的经济和安全。作为经受长期地质作用的自然产物,岩体是由大量不连续结构面(如:断层、节理、层理、裂隙等)相互切割形成的复杂结构体,这种复杂的结构特征使得岩体工程力学性参数的确定变得十分困难[1-3]。
目前,岩体工程力学参数确定方法主要包括物理试验方法、经验类比方法和数值试验方法三类。物理试验方法是确定岩体工程力学参数最直接的方法,但由于受试验条件、试样尺寸、试样数量和试验经费等限制,通过少量现场试验和一定数量的小尺寸室内试验,很难获得满足工程需求的岩体力学参数[4-7];经验类比方法是目前确定岩体工程力学参数最常用的方法,但这类方法缺少严密的理论基础和科学合理的定量依据,带有很强的人为主观性[8-9];随着计算机技术的飞速发展和数值仿真方法的进步,数值仿真试验为确定岩体工程力学参数提供了一条新的途径,但该类方法尚处于探索阶段,离实际工程应用还有较大距离[10-11]。因此对岩体工程力学参数确定方法的研究,一直是工程界和学术界广泛关注的热点和难点问题。
针对岩体工程力学参数合理确定的难题,从原位试验技术、定量类比方法和数值仿真试验三个方面开展了系统研究,形成了包含“一设备、一库、一平台”综合确定岩体工程力学参数的方法体系,如图1所示。
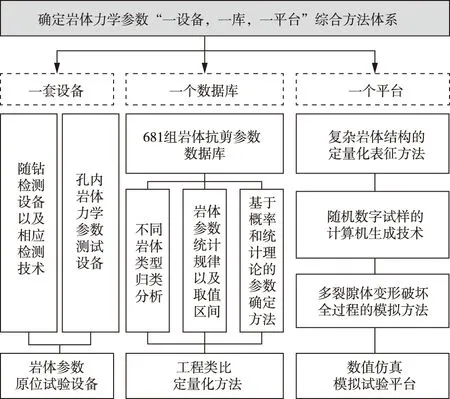
图1 确定岩体工程力学参数的方法体系
本文研发了岩体质量随钻测试和岩体力学参数原位试验的设备和技术,为通过原位试验快速获取岩体工程力学特性参数提供了新的手段;同时,提出了基于大样本岩体力学试验资料和数理统计理论确定岩体力学参数的定量类比法,使工程中常用的经验类比法具备了更为严密的理论基础。
2 岩体参数随钻测试和孔内原位试验技术
为解决现阶段岩石试验尺寸小、数量少、代
表性差等难题,研制了利用常规地质钻孔开展岩体原位试验的设备(岩体参数随钻测试设备和孔内岩体力学原位试验设备)以及相应的试验技术。
2.1 岩体参数随钻测试设备和技术岩体参数随钻测试设备由地质钻机以及加装在钻机上的压力传感器、转速传感器、扭矩传感器和激光位移传感器等组成,如图2所示。在钻机钻进过程中,可实时获取钻进压力、钻杆转速、钻进扭矩、钻进速度等钻进参数。通过对随钻实时钻进参数与岩层相关性的分析来获取岩体完整性、单轴抗压强度和耐磨性等工程特性指标[12-14]。

图2 新型岩体质量随钻检测设备
(1)利用钻进过程指数确定岩体完整性。以往研究通常采用钻进速度(V)来描述岩体质量,但大量随钻实测资料表明,即使在同一岩层中钻进速度(V)还会受到钻进压力(F)和钻杆转速(N)的影响(图3(a))。为此,提出了一种新的指标,即钻进过程指数(DPI)来定量评价岩体完整性(见式(1))。该指标综合考虑了钻进过程中F和N的影响,在均质材料中具有唯一性,且非常稳定,如图3(b)所示。
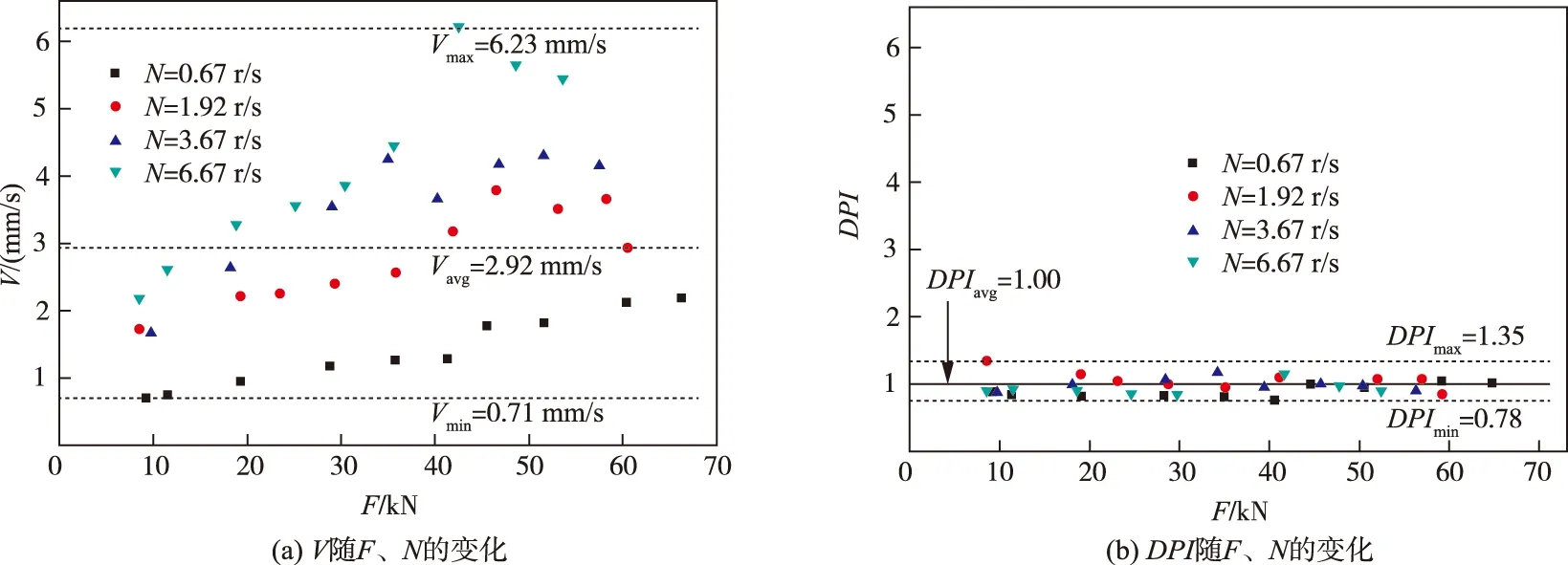
图3 钻进过程指数DPI
DPI=αF-0.53N-0.48V
(1)
式中α为与岩石类型相关的待定常量,可通过室内试验率定。
图4是某工程钻进过程指数随深度变化及其与岩芯的对比情况,可以看出该指标能很好地反映岩体性状的变化,当岩体较为完整时DPI在0~2之间。

图4 岩体钻进过程指数和完整性对应关系
为便于工程应用,进一步建立了DPI与岩体质量指标RQD的映射公式:
(2)
式中∑Li(0≤DPI≤2)为DPI处于0~2之间对应的岩芯长度,且Li≥10 cm。
对于图4中的裂隙岩体,根据式(2)得到的RQD为74,与采用传统岩芯量测得到的RQD(72)十分吻合。该方法不仅减少了以往统计RQD时人为主观因素的影响,而且为工程快速获取RQD提供了一种新方法。
(2)利用钻进切深斜率确定岩石单轴抗压强度。根据对随钻实测数据的分析发现,钻机钻进压力和单转钻进深度呈线性相关关系(图5(a)),且钻进切深斜率(Kslope)沿钻孔深度与不同岩层、不同岩性具有很好的对应性(图5(b))。据此,提出了通过钻进切深斜率确定岩石单轴抗压强度R的经验公式:
R=βKslope
(3)
式中:R为岩石单轴抗压强度,MPa;Kslope为切深斜率;β为与钻头型式有关的待定常量,取值范围为600~800。
图5(b)为某一工程地质钻探过程中,获得的各岩层钻进切深斜率和按式(3)计算得到的岩石单轴抗压强度,并给出了岩芯实测单轴抗压强度与计算结果的对比情况,两者高度一致,充分验证了本文方法的合理性,该方法为快速获得岩石单轴抗压强度提供了新的手段。
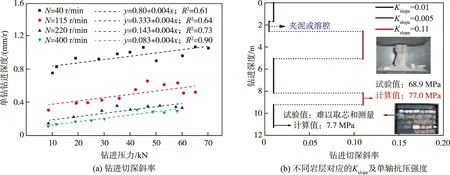
图5 利用钻进切深斜率确定岩石单轴抗压强度的方法
(3)利用单位体积钻进耗能评价岩石耐磨性。根据钻进过程中钻头的受力特征(图6(a)),建立了单位体积钻进耗能(ηe)的计算公式:
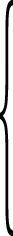
(4)
式中:Ec为钻进耗能,kJ;M为钻进扭矩,N·m;v为泊松比;R为钻头半径,mm;μ为钻头与岩石摩擦系数;t为钻进时间,s。
基于大量试验数据,建立了单位体积钻进耗能与岩石耐磨性指标(CAI)之间的定量关系(图6(b)):
CAI=0.807e0.0137ηe
(5)
图6(c)为按式(5)计算得到的CAI与试验实测结果的对比情况,可以看出两者吻合较好。本文方法为利用随钻检测信息快速获取岩石耐磨性指标提供了新的途径。
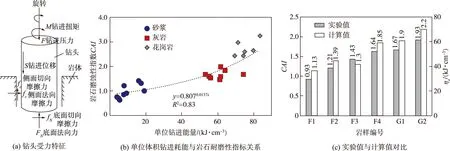
图6 岩体耐磨性指标确定方法
2.2 孔内岩体力学原位试验设备和方法研制的孔内岩体力学原位试验设备由控制平台、辅助装置和钻孔剪切弹模测头三部分组成(图7)。该设备能够在狭窄的勘探钻孔中进行岩体变形和抗剪原位试验,方便快捷地获得岩体变形和强度特性参数[15-17]。
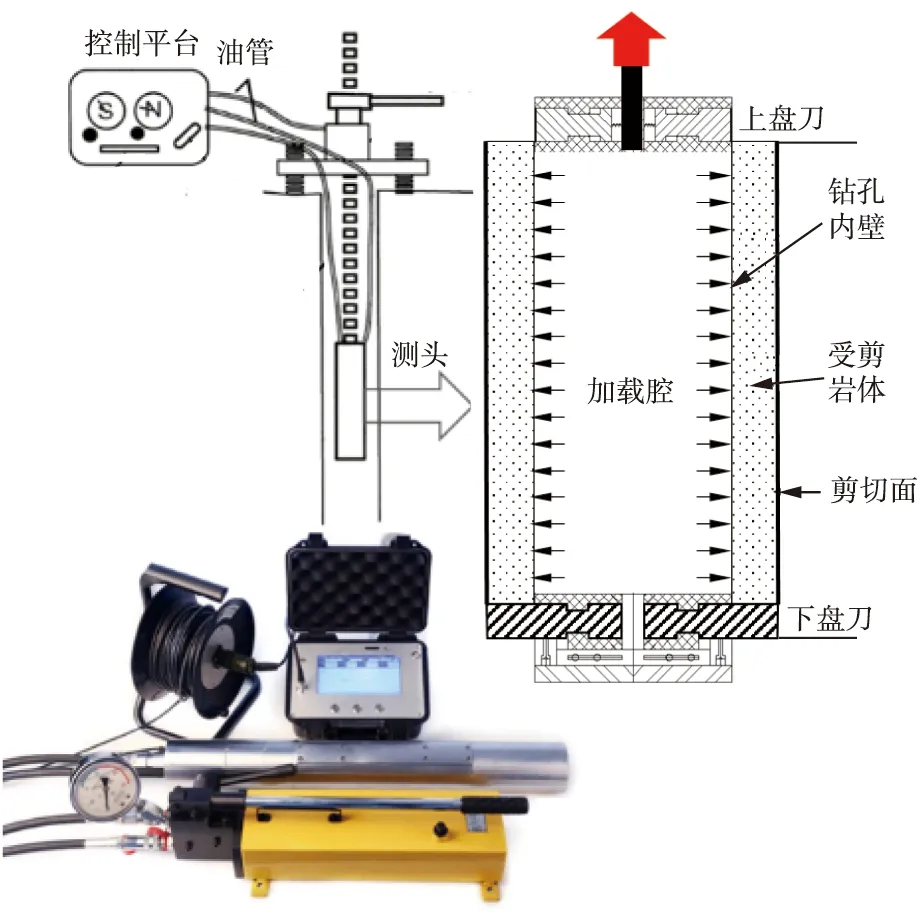
图7 孔内岩体力学原位试验设备
(1)钻孔弹模试验原理及方法。岩体钻孔弹模试验的工作原理与工程中常用的旁压试验原理相同,其理论基础为厚壁圆筒理论,利用圆筒内部压力和径向变形的关系来获取筒壁材料的变形模量,如图8(a)所示。在实际测试中,将岩体钻孔剪切弹模仪放置在岩体钻孔中的预定位置,利用上下盘刀之间的耐高压橡胶囊(加载腔)向孔壁岩体施加压力(P),根据橡胶囊油量变化确定孔壁岩体径向变形(δ),通过反复加卸载获得相应的P-δ过程曲线,如图8(b)(c)所示。

图8 钻孔弹模试验
钻孔弹模试验并不能直接得到岩体的弹性模量(E),需要进行一定的转化计算,国内外已给出了某些特定条件下的经验公式[7],这些经验公式在实际应用中存在较大的局限性。针对这一问题,本文进一步提出了一种基于优化算法,根据钻孔弹模试验结果直接反演计算考虑岩体结构和尺寸效应等复杂因素的岩体综合弹模(Ez)的方法,如式(6)所示。该方法以优化模型为核心,通过优化驱动岩体弹模、泊松比不断改变,对钻孔试验加载过程进行数值模拟,当数值模拟与试验曲线吻合度最高时对应的弹模、泊松比即为所求的最终结果。
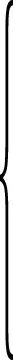
(6)
式中:δmi、δci分别为i荷载步下数值模拟和试验实测的孔壁变形;K、u和F分别为数值计算中的刚度矩阵、节点位移和荷载矩阵;A(ub)为根据孔壁节点位移(ub)计算孔壁变形(δci)的函数。
图9(a)为某一工程钻孔弹模试验实测的P-δ过程线,通过优化算法计算得到的弹性模量为17.24 GPa,图9(b)为最优解对应的孔周围岩应力变形分布情况。
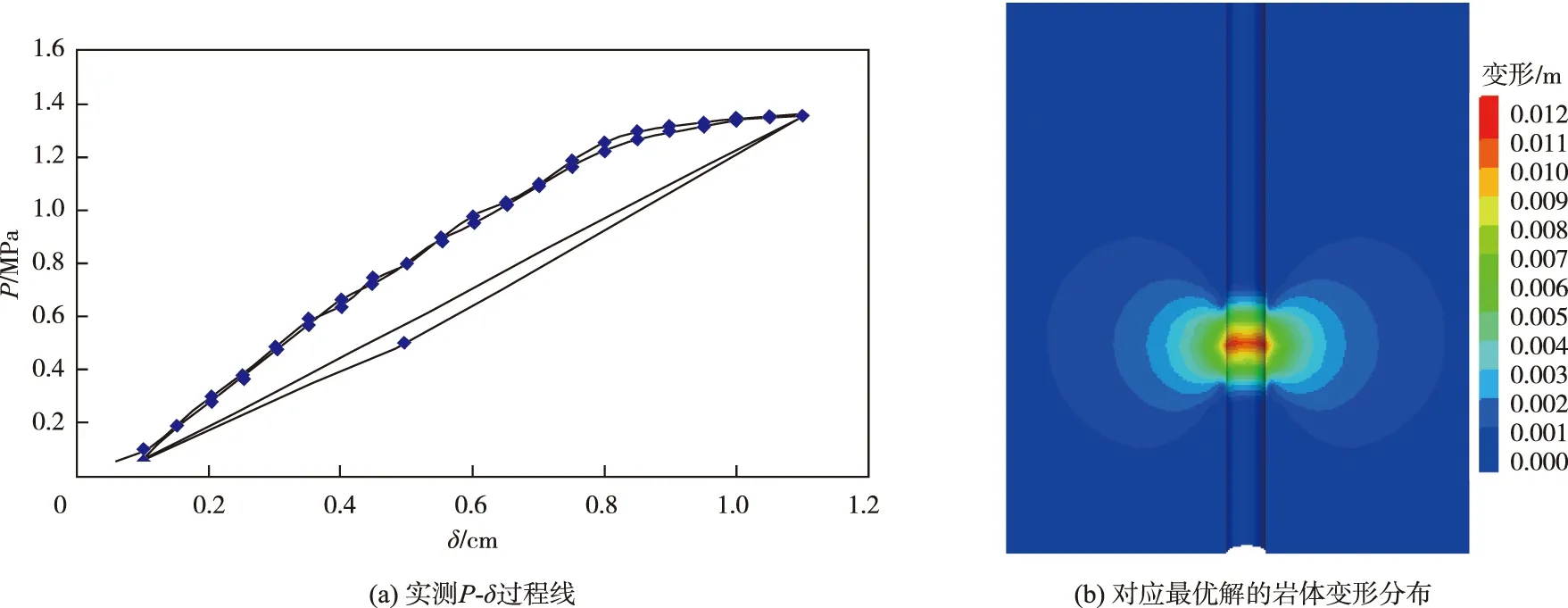
图9 某一工程钻孔弹模试验实例
(2)钻孔剪切试验原理及方法。当进行钻孔原位剪切试验时,首先利用安装在测头中的上下盘刀旋转掏槽,在上槽部位形成剪切临空面后收回上槽盘刀,并通过橡胶囊施加剪切试验的正应力,然后再上拔下槽盘刀进行剪切试验,根据试验实测的下盘刀最大上拔力和剪切面面积计算得到相应正应力下的岩体抗剪强度,如果在同一岩层中进行3~5组不同正应力下的剪切试验,即可按常规的试验数据整理方法快捷获得岩体剪切强度参数。图10(a)(b)(c)分别为钻孔剪切试验原理的示意图和室内试验验证结果。图11是钻孔原位剪切试验在某一工程的实际应用情况。
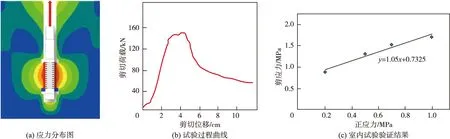
图10 基于钻孔剪切的岩体强度特性参数确定方法

图11 钻孔原位剪切试验工程应用实例
3 岩体力学参数的定量类比方法
如前所述,现阶段工程经验类比仍然是确定岩体力学参数的主要方法,参数确定合理与否很大程度上依赖于工程师对已有工程“经验资料”的掌握程度和类比分析方法的科学合理性。为解决“经验资料”不足的问题,本文对建国以来81个工程681组不同类型岩体(软弱夹层、无填充结构面和岩体)的抗剪强度试验成果进行了系统的整编,形成了岩体抗剪强度参数数据库,在此基础上深入研究了不同类型岩体抗剪强度参数的统计特性;并进一步探讨了基于Bayes方法和可靠度理论,利用已有数据库大样本资料和具体工程少量试验成果来确定岩体参数的定量类比方法[4,18]。
3.1 岩体现场抗剪试验资料数据库建成的岩体工程抗剪强度参数数据库,如图12所示,数据来源于全国19个省、81个工程,涵盖水利水电、交通和矿山等行业,包括每个试块的抗剪试验数据和破坏特征。这些试验数据具有宝贵的研究和应用价值。

图12 岩体工程抗剪强度数据库
在此基础上,借鉴已有岩体分类研究成果,根据不同的岩体类型和特征,建立了基于多因素定性描述和定量参数相结合的综合分类方法,如表1—3所示。

表1 软弱夹层分类标准表

表2 无填充结构面分类标准表

表3 岩体分类标准表
依据分类标准对各类岩体抗剪试验数据进行了归类分析,图13给出了两组典型的抗剪试验数据散点图。
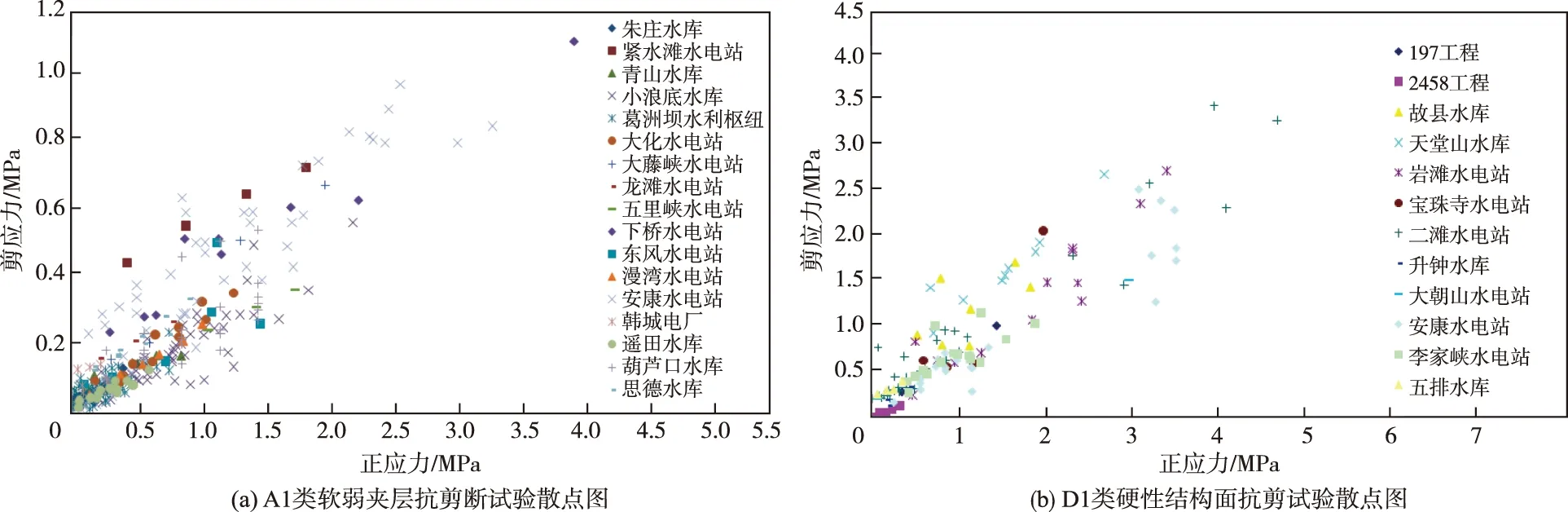
图13 抗剪参数归类分析
从图13可以看出,同类、同级别岩体的抗剪强度试验数据呈现出相对集中的趋势,表明本文所采用的分类标准和归类分析方法是合理可行的,归类分析成果基本上代表了各类岩体的实际情况。
3.2 抗剪强度试验成果统计分析从前述各类岩体归类分析的结果可以看出,不同岩性的岩体,其物理力学参数有很大差别;既便是岩性相同的岩体,由于各种影响因素的复杂性,其物理力学参数也会有一定程度的变化,具有随机不确定性,对于这些随机变量可采用数理统计方法来建立相应的概率统计模型,从整体上把握不同类型岩体力学参数的统计规律[8]。表4为通过统计分析获得的软弱夹层、无充填结构面和岩体抗剪强度参数(c、f)的概率统计模型以及相应于不同置信水平的取值范围。表中结果表明,各类岩体的抗剪强度参数具有很强的统计规律,所获得的分布概型和相应的统计特征参数在总体上代表了各类岩体抗剪强度参数的统计特征,同时,给出的抗剪参数取值范围可作为实际工程中判断参数取值是否合理的重要依据。这些统计结果无论在理论和实用上都具有十分重要的价值。
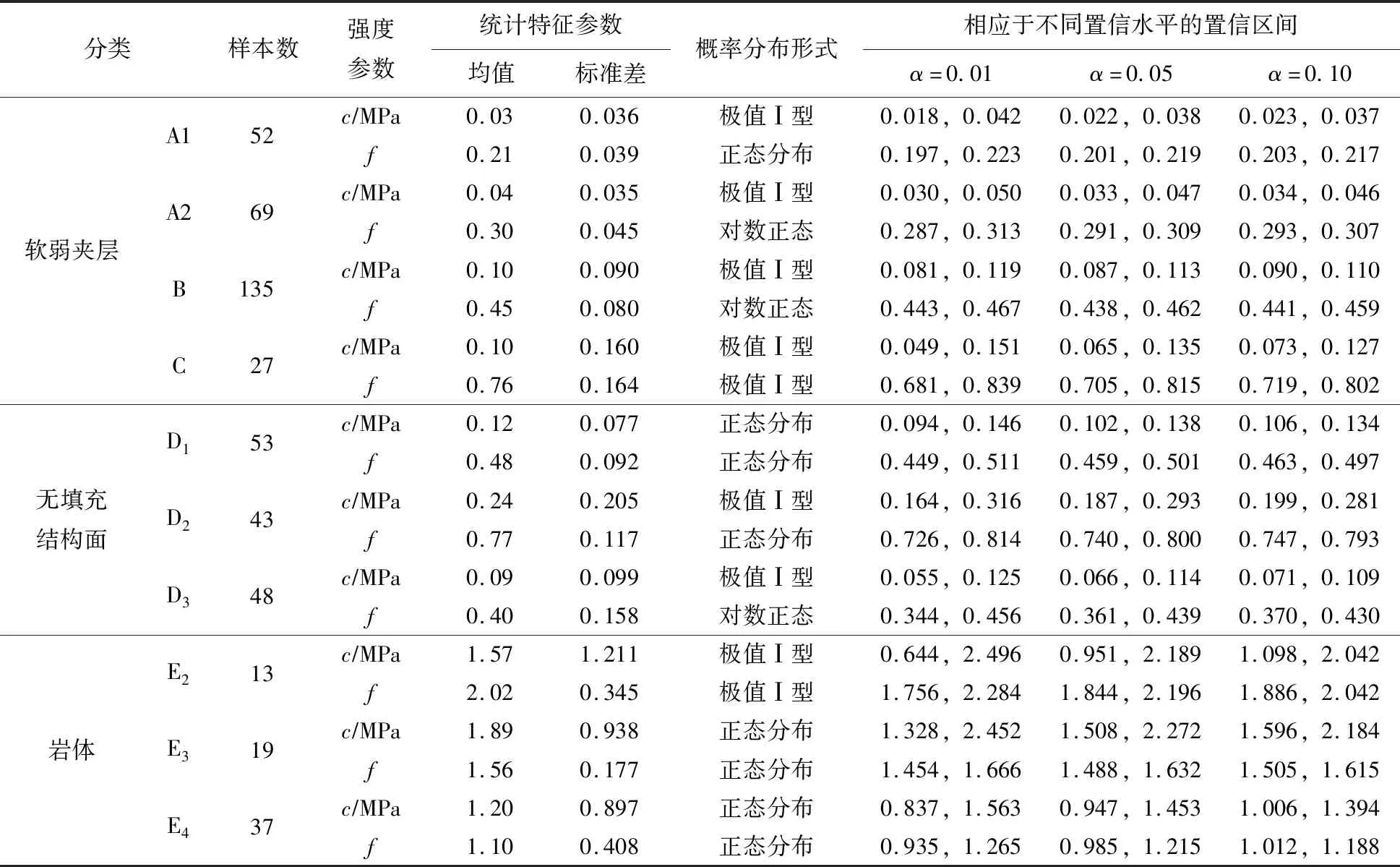
表4 软弱夹层抗剪强度试验参数统计分析结果
3.3 岩体抗剪强度参数确定方法如前所述,目前岩体抗剪强度参数的确定主要是依据某一工程有限的室内外试验成果,通过工程类比分析获得,所确定的参数带有很大的人为主观性。为了解决这一问题,引入概率统计中的Bayes方法[9]和可靠度理论,提出了一种从“试验值”“统计值”“标准值”到“设计值”的取值方法,其具体过程如图14所示。
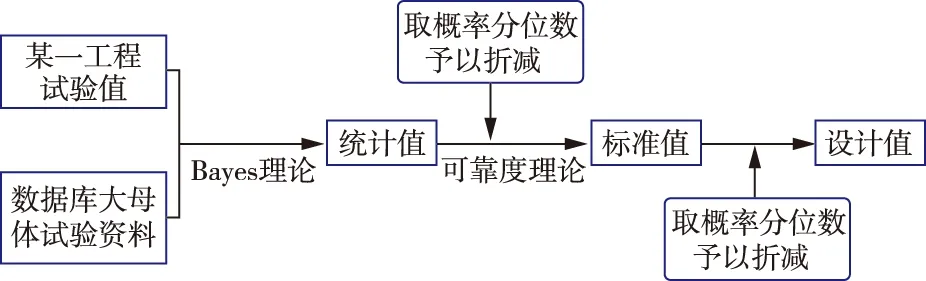
图14 基于Bayes方法和可靠度理论确定岩体抗剪强度的方法
(1)“统计值”的确定方法。每一个具体工程所做的有限数量的试验提供了图14中的“试验值”,已有工程积累的大量试验资料则提供了图14中的“经验值”。应用数理统计中的Bayes方法(式(7)),可将 “试验”和“经验”有机结合起来,获得岩体参数的大概率估计值(“统计值”),这种定量类比方法比过去依靠工程师人为判断的纯经验方法更为科学合理。当然,如果某一工程试验数量足够多,也可以直接通过对试验结果的统计分析获得岩体参数的“统计值”。
(7)
式中:P(Bi)为事件Bi(对应于数据库大样本资料)发生的先验概率;P(A/Bi)为事件Bi发生条件下事件A的条件概率(或称为试验概率,对应于某一具体工程的试验数据);P(Bi/A)为事件Bi(对应于统计值)的后验概率。如果已知大样本的先验分布P(Bi)和试验概率P(A/Bi),按式(8)和式(9)就可以对抗剪强度参数的统计结果做出新的估计(即图14中的“统计值”):
(8)
(9)
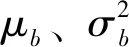
下面通过一个实例来说明Bayes方法的具体应用情况。某工程坝基辉绿岩弱风化带中有一组缓倾角夹泥裂隙,是控制坝基抗滑稳定的主要结构面。为此,进行了9组现场裂隙面抗剪试验,得出黏聚力c的均值为5.13×105Pa,从经验判断此值明显偏大[4]。现借助Bayes公式重新进行估算,根据同类岩体裂隙面抗剪试验26组的试验成果和该工程的9组试验成果,计算得到的后验概率分布列于表5中。黏聚力c的大概率估计值为:c=0.58×l.5+0.18×4.1+0.13×6.7+0.09×9.3+0.02×11.9+0×14.5=3.577×105Pa。

表5 抗剪强度参数c的Bayes公式计算结果
(2)“标准值”和“设计值”的确定方法。由Bayes方法求得的统计值,虽然反映了抗剪强度参数大样本的统计特性,但并不能直接应用于工程设计中,譬如假定某一参数服从正态分布,其均值为0.56,当标准差为0.08时,该参数小于均值的概率P(x<μ)可达50%,意味着采用该参数直接进入设计中会承担很大的风险。因此,“统计值”还需通过取概率分位数予以折减后变为“标准值”,再除以分项系数后才能作为设计采用值(“设计值”)。
考虑到岩体结构的复杂性和工程实际应用需求,抗剪强度参数的“标准值”可采用概率分布的0.2分位值(相应的概率保证率为80%)。对应于不同的分布概型,“标准值”可以按下面的公式计算。
当抗剪强度参数服从正态分布时:
μk=μb+Kσb
(10)
当抗剪强度参数服从对数正态分布时:
(11)
式中:μk为标准值;δb=σb/μb;K为与概率分位数有关的系数。实际工程中一般取概率分位数为0.2,此时K=-0.84。
如前所述,标准值仍然不能直接用于实际工程设计中,还必须要采用适当的分项系数γ进行折减后才能作为工程“设计值”,具体计算公式如下:
(12)
当抗剪强度参数服从正态分布时:
(13)
当抗剪强度参数服从对数正态分布时:
(14)
式中:μd为设计值;γ为分项系数;K1=φ-1(αf1)、K2=φ-1(αf2),αf1、αf2分别为参数设计值和标准值在其概率分布上的分位值,实际工程中一般取K1=-2、K2=-1.645。
表6给出了8个工程岩体抗剪强度参数(内摩擦系数f),利用上述方法确定设计值的过程。从表6可知,除了工程4、5以外,其余工程f≥fk的概率都在0.80以上,满足工程所需0.20概率分位数要求,可直接将此“标准值”应用于设计。工程4、5的P(f≥fk)偏小,需按式(13)或式(14)计算分项系数,经折减后得出设计值,以供设计应用。需要指出的是,对于“统计值”出现的概率己大于0.8的情况(如工程3和6),则无需修正,否则采用修正后参数进行设计将过于保守。
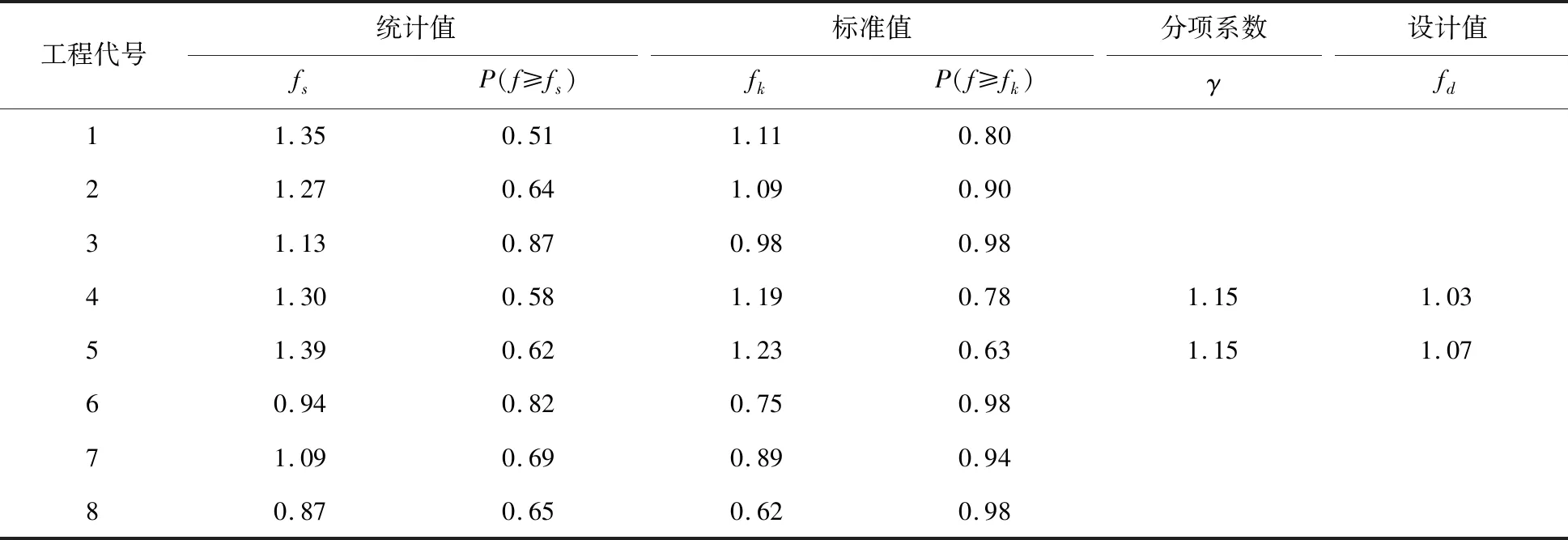
表6 8个工程岩体抗剪参数f设计值的确定过程
4 结论
(1)研制了岩体参数随钻测试和孔内原位试验设备,提出了根据随钻实时信息确定岩体完整性、单轴抗压强度和耐磨性参数的技术,以及通过孔内原位试验快速获得岩体强度和变形参数的方法,为实现岩体工程力学参数的快速测试提供了一种新的手段。
(2)构建了包含81个工程681组现场岩体抗剪试验资料数据库,提出了各类岩体抗剪强度参数的分布概型、统计特征值以及相应不同置信水平的取值区间,这些统计成果对于岩体抗剪参数取值具有重要的参考价值。
(3)基于Bayes方法和可靠度理论,提出了利用大样本数据库资料和少量具体工程试验成果来确定岩体参数的定量类比方法,有效解决了参数工程类比分析中科学定量化的难题。
