基于超螺旋滑模扰动观测器的永磁同步电机无传感器抗干扰控制策略研究

韩琨，张长征，袁雷

基于超螺旋滑模扰动观测器的永磁同步电机无传感器抗干扰控制策略研究

韩琨，张长征，袁雷

（湖北工业大学，武汉 430000）

提高包装行业中自动化设备的工作精准度，优化传统永磁同步电机无传感器控制系统的稳定性，提高电机遭遇内外扰动后的系统鲁棒性和抗扰动性能。引入超螺旋滑模算法，设计一种超螺旋滑模MRAS观测器来提高系统的稳定性，同时利用滑模扰动观测器对电机良好的动态进行性能追踪，利用超螺旋滑模算法对其进行性能优化，提出超螺旋滑模MRAS观测器和超螺旋滑模扰动观测器对永磁同步电机复合控制的策略。该方案有效降低了电机遭遇扰动时转速估计误差，误差在0.8 r/min附近波动，明显提高了电机控制系统遭遇干扰后的响应速度。在MATLAB/SIMULINK中进行实验仿真，结果表明所提控制策略提高了系统的鲁棒性和追踪精度，加强了系统的抗干扰能力。

永磁同步电机；超螺旋滑模；模型自适应观测器；滑模扰动观测器；动态追踪

近年来，随着国家经济不断发展，居民生活水平提高，包装行业高速发展，包装产业在给人们带来大量方便的同时也面临严峻的考验[1]。任何包装产业都需要自动化设备来提高工作效率，尤其是包装工艺复杂且具有难度的行业则更甚[2]。

影响包装产业发展的主要环节是伺服电机驱动系统，行业通过控制电机来完成精细的包装活动[3]，现在应用于包装领域的电机驱动系统大多数是以永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）为主的控制系统。在包装产业的发展过程中，电机控制技术也不断进步，逐渐从能耗高、性能差向高端发展[4-5]。无传感器控制技术已经逐渐成为现代电机控制技术的发展趋势，它通过检测电机绕组中的相关电信号，利用先进的控制算法对电机的实时运行状态进行监测，对转速、转矩等电机参数进行估计[6-9]。文献[10-12]介绍了模型参考自适应系统（Model Reference Adaptive System, MRAS），MRAS是现代电机控制技术中无传感器控制应用较广泛的一种，但是传统MRAS观测器中PI控制算法抗扰动能力和鲁棒性能一般。文献[13-14]介绍了超螺旋算法及二阶滑模控制基本原理，表明二阶滑模可以提高系统的鲁棒性。文献[15-17]通过对传统滑模控制进行介绍，表明滑模控制是一种特殊的非线性控制系统，应用于很多领域和行业，滑模面和滑模增益是影响其稳定性的2个因素，合适的参数设置可以使被控对象在达到快速收敛目的同时避免由增益过大导致电机运行过程中出现过度抖振的现象。文献[18-20]介绍的滑模扰动观测器可以用于系统的负载监测和跟踪反馈，当系统受到扰动时，扰动观测器会估计扰动误差并前馈至系统，系统进行及时调整。

文中设计的超螺旋滑模MRAS观测器可提高系统的鲁棒性和稳定性，扰动观测器可以有效地对系统外部扰动和内部扰动进行监测，结合超螺旋滑模与滑模扰动观测器的优点，提出超螺旋滑模扰动观测器来提高系统的抗干扰能力；并且提出复合控制的策略提高系统的抗干扰能力和鲁棒性能，通过仿真验证所述方法的有效性。

1 PMSM数学模型

PMSM是一个强耦合，复杂且难以控制的非线性系统，为了更好地控制三相PMSM，文中选择同步旋转坐标系–下的数学模型，其定子电压方程为：

磁链方程为：

电磁转矩方程为：

运动方程为：

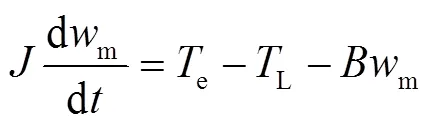
2 超螺旋滑模模型自适应观测器

MRAS是自适应系统的一种控制策略，MRAS包含可调模型、参考模型和自适应律3个部分。MRAS的工作原理是利用参考模型和可调模型的输出量之差作为信号，通过所确定的自适应律来实现对PMSM的参数辨识并反馈到控制系统中。因此，自适应律的稳定直接影响到MRAS观测器的性能，而传统MRAS观测器中的PI自适应律鲁棒性低，当系统扰动较大时会引起电机系统的不稳定。文中引入一种优于PI自适应律的超螺旋滑模自适应律来提高系统的鲁棒性，下面介绍传统MRAS观测器的工作过程。

2.1 传统MRAS观测器设计

由表贴式三相PMSM数学模型得到定子电流方程如下：

为得到可调模型，不妨定义：

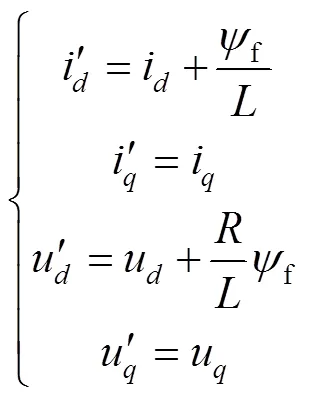
则得到可调模型为：

写成状态空间表达式，即：

状态空间表达式变为：

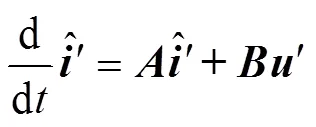
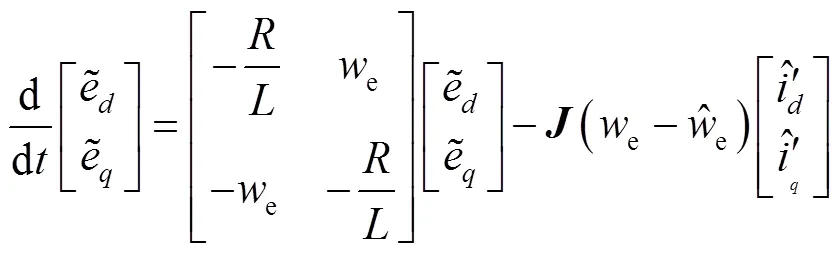
根据Popov超稳定性理论可得：

对其积分可以求得转子位置估计值：

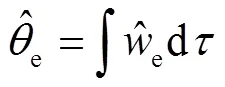
传统MRAS观测器的实现框图见图1。

2.2 超螺旋滑模自适应律

超螺旋滑模属于滑模变结构的一种，具有对参数变化不敏感、鲁棒性强、动态性能好等优点。超螺旋滑模独特的二阶滑模结构可以降低传统一阶滑模变控制的抖振现象，在PMSM出现扰动变化时保证平滑稳定的输出。式（16）给出超螺旋滑模的基本形式。

下面设计超螺旋滑模MRAS控制器，采用超螺旋滑模自适应律对传统MRAS观测器进行优化，设置滑模面：

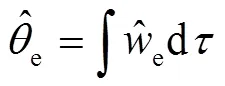
2.3 稳定性证明

根据Lyapunov定理，选取状态矢量为：

代入得：

3 超螺旋滑模扰动观测器

3.1 PMSM扰动观测器设计

由PMSM的机械运动方程和转矩方程可以得到PMSM动态方程：

定义电机参数及参数的变化量为：

式中：n、n、n为常规参数变量；∆n、∆n、∆n为参数变化量，那么在考虑电机运行过程中内部参数变化和外部扰动情况下，可得：

结合式（28）重写电机运动动态方程，可得：

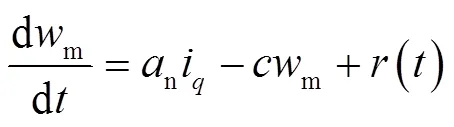
滑模扰动观测器控制框图见图2。

3.2 超螺旋滑模扰动观测器

根据PMSM动态方程构建滑模扰动观测器方程：

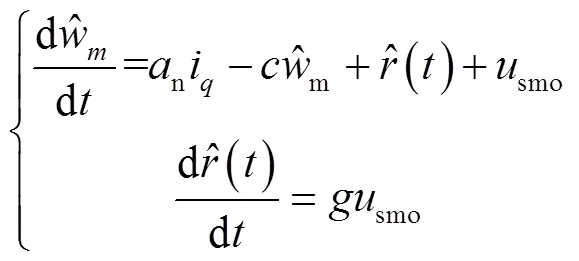
超螺旋滑模对传统滑模扰动观测器进行优化，提高系统扰动观测速度和反馈灵敏度，在电机出现内部扰动和负载突变的情况时，迅速捕捉到扰动情况，实时估计扰动并前馈到转速控制环节中，提高系统的抗干扰能力。

结合式（16）可得超螺旋滑模扰动观测器方程：

与动态方程相减可以得到误差动态方程：

3.3 PMSM复合控制策略

PMSM转速范围广，负载变化大，传感器无法时时刻刻对电机参数保持较高的捕捉灵敏度，长时间的工作运行会导致电机的电阻、电感、永磁体发生变化。本文基于超螺旋滑模扰动观测器与超螺旋滑模MRAS观测器提出了复合控制策略：超螺旋滑模MRAS观测器对电机参数进行实时捕捉和计算，并将部分系统参数反馈到超螺旋滑模扰动观测器；对超螺旋滑模扰动观测器系统扰动进行实时监测，将扰动估计值前馈至转速环，提高转速控制环对系统参数的反应灵敏度，提高系统抗扰动的能力和鲁棒性能，达到复合控制的目的。控制框图见图3。

图3 基于超螺旋滑模控制的PMSM无传感器控制系统的控制框图

4 仿真实验

文中以MATLAB/SIMULINK为平台进行仿真研究来验证2种观测器的有效性。为了验证超螺旋滑模MRAS观测器和超螺旋滑模扰动观测器的性能，文中设计了3种仿真研究方案。

1）方案1，主要验证所设计的超螺旋滑模MRAS观测器的有效性，即速度控制器采用PI，将速度观测器分别采用传统MRAS观测器和超螺旋滑模MRAS观测器进行对比仿真分析。

2）方案2，主要验证所设计的超螺旋滑模扰动观测器的有效性，即速度控制器采用PI，将扰动观测器采用传统滑模观测器和超螺旋滑模扰动观测器进行对比仿真分析。

3）方案3，主要验证所设计的复合控制策略的有效性，即PI控制，将单一超螺旋滑模MRAS观测器控制和复合控制进行对比仿真分析。所用SPMSM参数见表1。

表1 电机参数

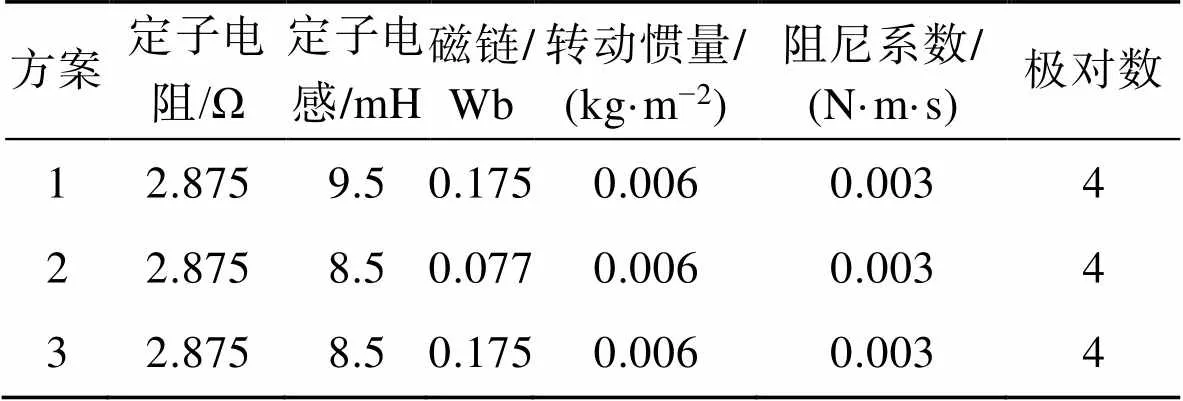
Tab.1 Motor parameters

4.1 2种MRAS观测器对比仿真分析

系统额定转速为1 000 r/min，电机空载启动，在0.2 s时突加负载20 N·m，0.4 s时突降负载至10 N·m，对2种观测器设置合适参数，使系统达到稳定，分别从转速估计误差和转子位置估计误差两方面来进行对比，仿真结果见图4—5。

从图4仿真结果可以看出，当电机从零速上升到参考转速1 000 r/min时，2种观测器都有一定的超调量。0.2 s负载突变时对比2种MRAS观测器可知，超螺旋滑模MRAS观测器转速恢复时间为0.054 s，传统MRAS观测器转速恢复时间为0.061 s；0.4 s负载突变时对比2种MRAS观测器可知，超螺旋滑模MRAS观测器转速恢复时间为0.045 s，传统MRAS观测器转速恢复时间为0.051 s。由图4—5可知，改进后的超螺旋滑模MRAS观测器在负载突变时转速恢复时间较短，滑模动态稳定性好，较传统MRAS观测器系统鲁棒性能提高。在负载突变时分析转速估计误差和转子位置估计误差，传统MRAS观测器的转速估计误差波动量为60 r/min，转子位置估计误差波动量为6 r/min，超螺旋滑模MRAS观测器转速估计误差波动量稳定在0，转子位置估计误差波动量为0。

图4 传统MRAS观测器的仿真结果

图5 超螺旋滑模MRAS观测器的仿真结果

仿真结果验证了改进后的超螺旋滑模MRAS观测器的有效性，提高了系统受到扰动后的反应灵敏度，转速误差和转子位置误差波动稳定在0附近，具有光滑平稳的工作波形，提高了系统的鲁棒性能和动态稳定性。

4.2 2种滑模扰动观测器对比仿真分析

系统额定转速为1 000 r/min，电机空载启动，在0.2 s时突加负载20 N·m，0.4 s时突降负载至10 N·m，对2种扰动观测器设置合适参数，使系统达到稳定，分别从转矩估计误差和转矩跟踪效果两方面来进行对比，仿真结果见图6—7。

图6 传统滑模扰动观测器的仿真结果

图7 超螺旋滑模扰动观测器的仿真结果

从图6可以看出，当电机负载突增至20 N·m，传统滑模扰动观测器的超调量为8.8 N·m，当负载降至10 N·.m时，有良好的追踪效果；在0.2 s时，转矩估计误差为21.2 N·m；在0.4 s时，转矩估计误差为7.4 N·m，说明负载变化量过大时，传统滑模扰动观测器追踪效果一般。

从图7可以看出，当电机负载突增至20 N·m，超螺旋滑模扰动观测器超调量为0，2次负载变化都有较好的追踪效果；在0.2 s时，转矩估计误差为16.31 N·m；在0.4 s时，转矩估计误差为7.8 N·m。仿真结果验证了超螺旋滑模扰动观测器的有效性，在负载变化大的情况下仍保持良好的追踪效果，追踪曲线光滑，贴合实际工作曲线。

4.3 3种控制策略对比仿真分析

系统额定转速为1 000 r/min，电机空载启动，在0.2 s时突加负载20 N·m，0.4 s时突降负载至10 N·m，对3种控制策略设置合适参数，使系统达到稳定。对3种控制策略的电机转速、转矩，以及系统的动态稳定和鲁棒性进行分析判断，仿真结果见图8—9。

从图8分析可知，当电机零速启动和负载变化时，3种控制策略都有一定的转速超调量，根据表2分析传统PI控制、超螺旋滑模MRAS观测器控制和复合控制下的转速恢复时间。其中复合控制策略的收敛速度最快为0.05 s，传统PI控制的转速恢复时间为0.063 s，超螺旋滑模MRAS观测器控制的转速恢复时间为0.054 s，结果表明复合控制中的超螺旋滑模扰动观测器可以明显提高系统的抗干扰能力。从图8分析3种控制策略的稳态性能，当电机稳定工作时，根据表2分析3种控制策略的转速估计误差和转速平稳度，其中复合控制转速估计误差最小，为0.1 r/min，且转速曲线平稳光滑，结果表明了复合控制提高了电机转速的动态稳定性和系统鲁棒性。

从图9分析可知，当电机处于稳定状态时，超螺旋滑模MRAS观测器的系统具有滑模控制的优良特性，没有明显的抖振，同时也具有3种控制策略中稳定的输出转矩；超螺旋滑模扰动观测器的复合控制具有最好的动态稳定性。根据表2分析3种控制策略的转矩恢复时间、稳态下的转矩超调量和转矩平稳度。其中复合控制的转矩恢复时间最短（0.012 s），传统PI控制的转矩恢复时间最长（0.03 s），并且对负载干扰响应的灵敏性一般；单一超螺旋滑模MRAS观测器对负载干扰响应的灵敏性略高于传统PI的，但都远低于加入超螺旋滑模扰动观测器复合控制策略的。

根据表2可知，当电机稳态时，3种控制策略中复合控制的转矩超调量最低（0.017 N·m），且转矩曲线平稳光滑；超螺旋滑模MRAS观测器控制的转矩超调量为0.025 N·m；传统PI控制的转矩超调量最大（0.20 N·m），且转矩曲线波动较大。结果表明，加入了超螺旋滑模扰动观测器的复合控制提高了电机转矩的动态稳定性和系统鲁棒性，并具有良好的转矩跟踪性。

图8 3种控制策略下的转速结果

图9 3种控制策略下的转矩结果

表2 3种控制策略的结果对比

Tab.2 Comparisons of results under three control strategies

5 结语

PMSM在工作中容易受到外部和内部扰动的影响，使得系统呈现鲁棒性低，抗干扰能力弱，针对以上问题，文中提出超螺旋滑模MRAS观测器和超螺旋滑模扰动观测器二者复合控制的策略。仿真实验结果表明，当受到扰动时复合控制策略对电机的参数敏感度最高,这极大地提高了系统的动态稳定性和鲁棒性，有利于无传感器控制下对电机参数的预测，使得系统在受到频繁干扰的情况下仍然可以保持良好的工作能力。下一步工作将超螺旋控制策略进行实际的应用，在实际工作情况中找寻不足，进行完善。

[1] 何瑞. 电机无速度传感器控制技术在包装生产线中的应用[J]. 包装工程, 2022, 43(7): 233-237.

HE Rui. Application of Motor Speed Sensorless Control Technology in Packaging Production Line[J]. Packaging Engineering, 2022, 43(7): 233-237.

[2] 金爱娟, 项硕, 李少龙. 永磁同步电机全速范围内无传感控制策略研究[J]. 包装工程, 2020, 41(17): 171-181.

JIN Ai-juan, XIANG Shuo, LI Shao-long. Sensorless Control Strategy of PMSM in Full Speed Range[J]. Packaging Engineering, 2020, 41(17): 171-181.

[3] 薛建峰, 王景芹, 杨昭. 多感应电机相邻交叉耦合快速终端滑模同步控制[J]. 包装工程, 2017, 38(7): 173-177.

XUE Jian-feng, WANG Jing-qin, YANG Zhao. Synchronous Control of Adjacent Cross Coupling Fast Terminal Sliding-Mode Control for Multi Induction Motor[J]. Packaging Engineering, 2017, 38(7): 173-177.

[4] 缪仲翠, 王志浩, 李东亮, 等. 基于FOSM-MRAS观测器的永磁同步电机MPTC系统[J]. 电机与控制学报, 2020, 24(4): 121-130.

MIAO Zhong-cui, WANG Zhi-hao, LI Dong-liang, et al. Permanent Magnet Synchronous Motor MPTC System Based on FOSM-MRAS Observer[J]. Electric Machines and Control, 2020, 24(4): 121-130.

[5] 金爱娟, 尹晨滨, 李少龙, 等. 包装机驱动控制系统中谐波噪声信号抑制策略[J]. 包装工程, 2022, 43(3): 234-243.

JIN Ai-juan, YIN Chen-bin, LI Shao-long, et al. Suppression Strategy of Harmonic Noise Signals Contained in Packaging Machine Drive Control System[J]. Packaging Engineering, 2022, 43(3): 234-243.

[6] WOLDEGIORGIS A T, GE Xing Lai, WANG Hui Min et al. A New Frequency Adaptive Second-Order Disturbance Observer for Sensorless Vector Control of Interior Permanent Magnet Synchronous Motor[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11847-11857.

[7] 毛亮亮. 电动汽车永磁同步电机电流分段优化控制策略研究[D]. 哈尔滨: 哈尔滨理工大学, 2016: 25-45.

MAO Liang-liang. Research on Current Subsection Optimization Control Strategy of Permanent Magnet Synchronous Motor for Electric Vehicle[D]. Harbin: Harbin University of Science and Technology, 2016: 25-45.

[8] 孙恺英. 永磁同步电机无速度传感器状态估计及控制策略研究[D]. 天津: 天津大学, 2019: 15-35.

SUN Kai-ying. A Research on State Estimation of Speed Sensorless and Control Strategy for Permanent Magnet Synchronous Motor[D]. Tianjin: Tianjin University, 2019: 15-35.

[9] LEE K, HAN Y S. Reactive-Power-Based Robust MTPA Control for v/f Scalar-Controlled Induction Motor Drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 169-178.

[10] LEE W, KIM J, JANG P. On-Line MTPA Control Method for Synchronous Reluctance Motor[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 356-364.

[11] NGUYEN T H, NGUYEN T T, NGUYEN V Q, et al. An Adaptive Sliding-Mode Controller With a Modified Reduced-Order Proportional Integral Observer for Speed Regulation of a Permanent Magnet Synchronous Motor[J]. IEEE Transactions on Industrial Electronics, 2022, 69(7): 7181-7191.

[12] 闵磊. 基于超螺旋滑模MRAS的PMSM无位置传感器控制方法[D]. 青岛: 青岛大学, 2021: 30-50.

MIN Lei. Sensorless Control Method of PMSM Based on Super Spiral Sliding Mode MRAS[D]. Qingdao: Qingdao University, 2021: 30-50.

[13] 方馨. 压电驱动式FTS的跟踪控制策略研究[D]. 沈阳: 沈阳工业大学, 2020: 35-45.

FANG Xin. Research on Tracking Control Strategy of Piezoelectric Driven FTS[D]. Shenyang: Shenyang University of Technology, 2020: 35-45.

[14] 李涛. 采用扩展滑模观测器的数控机床永磁同步电机鲁棒控制方法[J]. 制造技术与机床, 2022(5): 152-158.

Li Tao. Robust Control Method for Permanent Magnet Synchronous Motor for NC Machine Tool Using Extended Sliding Mode Observer[J]. Manufacturing Technology & Machine Tool, 2022(5): 152-158.

[15] SONG Jun-zheng, WEI Xing, NIU Yu-gang. Self- Triggered Sliding Mode Control for Networked PMSM Speed Regulation System: A PSO-Optimized Super-Twisting Algorithm[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 763-773.

[16] 周华伟, 于晓东, 高猛虎, 等. 基于不匹配干扰观测器的圆筒型永磁直线电机新型滑模速度控制[J]. 中国电机工程学报, 2018, 38(7): 2163-2170.

ZHOU Hua-wei, YU Xiao-dong, GAO Meng-hu, et al. Novel Sliding Mode Speed Control for Tubular Permanent Magnet Linear Motors Based on Mismatched Disturbance Observers[J]. Proceedings of the CSEE, 2018, 38(7): 2163-2170.

[17] 陈玄. 基于滑模扰动观测器的永磁同步电机控制[D]. 株洲: 湖南工业大学, 2021: 20-27.

CHEN Xuan. Control of Permanent Magnet Synchronous Motor Based on Sliding Mode Disturbance Observer[D].Zhuzhou: Hunan University of Technology, 2021: 20-27.

[18] LI Ke, WANG Yi. Maximum Torque per Ampere (MTPA) Control for IPMSM Drives Using Signal Injection and an MTPA Control Law[J]. IEEE Transactions on Industrial Informatics, 2019, 15(10): 5588-5598.

[19] 颜渐德, 王辉, 兰永红, 等. 基于干扰观测器的永磁同步电动机滑模控制[J]. 微特电机, 2019, 47(1): 70-73.

YAN Jian-de, WANG Hui, LAN Yong-hong, et al. Disturbance Observer-Based Sliding Mode Control for Permanent-Magnet Synchronous Motor[J]. Small & Special Electrical Machines, 2019, 47(1): 70-73.

[20] 刘旭东, 李珂, 张奇, 等. 基于非线性扰动观测器的永磁同步电机单环预测控制[J]. 中国电机工程学报, 2018, 38(7): 2153-2162.

LIU Xu-dong, LI Ke, ZHANG Qi, et al. Single-Loop Predictive Control of PMSM Based on Nonlinear Disturbance Observers[J]. Proceedings of the CSEE, 2018, 38(7): 2153-2162.

Sensorless Anti-disturbance Control Strategy of Permanent Magnet Synchronous Motor Based on Super-twisting Sliding Mode Disturbance Observer

HAN Kun, ZHANG Chang-Zheng, YUAN Lei

(Hubei University of Technology, Wuhan 430000, China)

The work aims to improve the working accuracy of automation equipment in the packaging industry, optimize the stability of the sensorless control system of the traditional permanent magnet synchronous motor, and improve the system robustness and anti-disturbance performance when the motor encounters internal and external disturbances. A super-twisting sliding mode was introduced to design a super-twisting sliding mode MRAS observer to improve the stability of the system. Simultaneously, according to the good dynamic tracking performance of the sliding mode disturbance observer for the motor, the super-twisting sliding mode algorithm was used to optimize its performance. Besides, a combined control strategy of a super-twisting sliding mode MRAS observer and a super-twisting sliding mode disturbance observer for permanent magnet synchronous motors was proposed. This scheme effectively reduced the speed estimation error when the motor encountered disturbances, and the error fluctuated around 0.8 r/min, which significantly improved the response speed of the motor control system after encountering disturbances. The experimental simulation is carried out in MATLAB/SIMULINK, and the results verify that the control strategy proposed not only improves the robustness and tracking accuracy of the system, but also strengthens the anti-interference ability of the system.

permanent magnet synchronous motor; super-twisting sliding mode; model reference adaptive system; sliding mode disturbance observer; dynamic tracking

TM351

A

1001-3563(2023)03-0139-09

10.19554/j.cnki.1001-3563.2023.03.017

2022−07−31

国家自然科学基金（51507188）；国防科技重点实验室基金（6142217210301）；湖北工业大学博士科研启动基金（XJ2021000302）

韩琨（1999—），男，硕士生，主攻永磁同步电机控制方向。

张长征（1978—），男，博士，副教授，主要研究方向为电能质量与可再生能源发电系统；袁雷（1984—），男，博士，讲师，主要研究方向为电力电子与电力传动。

责任编辑：曾钰婵