一题多变,变中求道
——以平行线中的拐点问题为例
2023-02-15西华师范大学陈星颖
西华师范大学 陈星颖
教师可以立足于一个知识点,通过改变某些条件或者结论等一题多变的方式演变成多道题.通过对多道题的探索,引导学生从“变”中找“不变”,在“不变”中找到解决问题的方法,提高学生的解题能力.下面笔者结合教材中的一道练习题进行论述.
1 原题呈现

图1
(新人教A版七年级下册第五章第三节的习题)如图1,如果AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( ).
分析:该题是一个典型的平行线中的拐点问题,其中C是拐点.图1已经给出了平行线中拐点问题作辅助线的方法,学生能够很容易根据平行线的性质得出答案.但在各类测试中,对该类问题的考查比教材中的题目更加复杂,因此笔者通过改变提问、改变拐点的位置、改变拐点的个数、改变题目条件、改变问题情境、结论与条件互换的变式来提高学生的解题能力.
2 原题变式
2.1 改变提问
问题是数学的心脏,改变提问的方式可以充分挖掘题目的内涵.通过一题多问,延伸题目的外延,发散学生的思维.
变式1条件不变,∠ACE与∠BAC,∠CEF有什么数量关系?
变式2条件不变,∠ACE与∠BAC的补角和∠CEF的补角有什么数量关系?
变式3条件不变,能否用∠ACE表示∠BAC与∠CEF的和?
分析:若直接提问角的度数之和为多少,学生很容易得出,可能不会思考题中未提及的角之间有什么关系?通过提问角的数量关系是什么,以及∠ACE与其他两角的补角关系如何,让学生牢固掌握这道题所涉及到的知识点.不管问题怎么变,先抓住平行线的性质,然后找到这三条平行线所涉及的角的关系,最后解决问题.
2.2 改变拐点的位置
平行线中的拐点不仅可以在两平行线之内,也可以在两平行线之外.虽然拐点位置灵活多变,但解题也是有规律可寻的.
变式4在图2~5中,已知AB∥CD,那么∠B,∠D和∠E的数量关系是什么?

图2
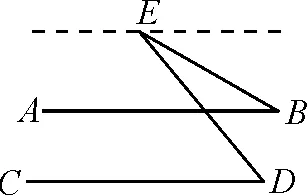
图3

图4

图5
分析:通过拐点位置的变化,让学生明确平行线中拐点问题的辅助线添加规律以及解题的一般步骤.不管拐点是在平行线的内部,还是在平行线的外部,添加辅助线的规律都是过拐点作已知直线的平行线.解题时,都是将拐点涉及的∠E,运用平行线的性质,转换为用∠B,∠D或与∠B,∠D相关的角表示,最后找到∠B,∠D和∠E的关系.
2.3 增加拐点的个数
拐点不仅位置灵活,其个数也可变化.增加拐点个数可促进学生深入探究各拐点间的关系.
变式5在图6(或图7),已知AB∥CD,∠ABE和∠CDE的平分线相交于点F,若∠E=80°,求∠F的度数.
变式6如图8,已知AM∥CN,∠MBE和∠NDE的平分线相交于点F,若∠E=80°,求∠F的度数.

变式8如图10,已知AB∥CD,则∠E1+……+∠En与∠B+∠F1+……+∠Fn-1+∠D的数量关系是什么?
变式9如图11,已知AB∥CD,则∠1+∠2+……+∠n等于多少度?

图6
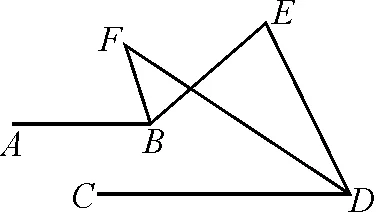
图7

图8

图9
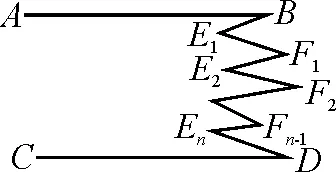
图10
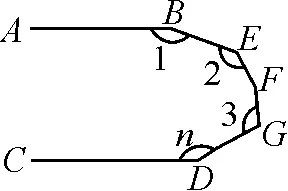
图11

2.4 改变题目中的条件
2.4.1 改变题目中的非本质条件
改变题目中的非本质条件,把题目条件减弱,可以提高题目的难度,让学生在找到解题办法后深化解题思路.

分析:将条件从特殊变换到一般,辅助线的作法与解题思路不变.条件弱化后,学生将注意力放在解题过程中的方法,梳理这类题型的解法,进而形成解题体系.
2.4.2 改变题目的本质条件
平时的练习题大多属于结构良好的问题,而在具体的考题中,学生可能会遇到结构不良的问题,改变题中的本质条件可促使学生拓宽解题思路.
变式11如图12,当AB与CD不平行时,连接MN,且MN同时平分∠BME和∠DNE,则∠AME,∠CNE,∠MEN的数量关系是什么?
变式12如图13,AB∥CD,∠BED,∠ABE,∠CDE之间有什么数量关系?若E在OM射线上运动时,∠BED,∠ABE,∠CDE又有什么数量关系?

图12

图13

2.5 改变问题情境
改变问题的情境,可以让学生在复杂的情境中识别拐点模型.
变式13如图14,将一块含30°的直角三角板放置在平行四边形中,求∠1+∠2的度数.

图14

图15
变式14将一副三角板的两直角边和一张对边平行的纸条按图15摆放,求∠1的度数.

图16
变式15如图16,小刀的刀柄外形是一个直角梯形(挖去一个半圆),刀片上下平行,转动刀片时形成∠1与∠2,求∠1+∠2的度数.
分析:改变情境会增加对学生的干扰,增加线段会隐藏拐点.首先引导学生观察题中的平行关系,如AB∥CD,平行的纸条或刀片.其次,找到拐点,抽离出其中的拐点模型,利用对应的角度关系解决问题.
2.6 结论与条件互换
将条件与结论互换也可以让学生深度挖掘题目蕴涵的知识点.教材中的题是根据平行求角度,考查平行线的性质.我们还可以根据角度大小运用平行线的判定定理,证明直线的平行关系.同样地,上述有些变式也可以将条件与结论互换,引起学生的深入思考.
平行线中的“拐点”问题是有难度的,特别是其形式多变,通过一题多变的形式可以帮助学生找到解决“拐点”问题的方法.解决拐点问题最重要的是找到辅助线的添加规律以及涉及的角度关系,辅助线的添加一般是过拐点作已知直线的平行线,平行线有可能不是水平放置,需要自己识别.没有平行条件时,则需要观察思考,构造出平行线.找角度关系时,不仅要考虑题干中提到的角,还要思考这个角的余角、补角以及特殊的平角、周角等.本文中通过层层递进的变式提升学生的解题能力,形成解题的体系.
