一种用于高频S 参数的去嵌算法
2023-02-14徐小明朱国林季振凯
纪 萍,徐小明,朱国林,季振凯
(无锡中微亿芯有限公司,江苏 无锡 214072)
0 引言
随着高速传输信号速率的不断增高,印制电路板(PCB)的信号完整性研究对整个通信系统的电气性能来说至关重要[1]。其中对PCB 高速信号质量的测量和管控是信号完整性研究中的重要一环。S 参数是利用频域来描述高速信号通道特性的一种方式,可通过S 参数提取插入损耗、回波损耗、串扰等信息来对信号的质量进行评价[2]。
在利用仪器对S 参数进行测量时,因为待测器件(DUT)的接口与测试仪器的接口不一致,需要通过夹具进行连接,而夹具的存在会影响测试结果。如何准确地去除夹具的影响,得到想要的DUT 的S 参数是一个值得研究的课题[3]。
1 设计背景
目前常用的去嵌方法可分为两类:第一类是设计一些专门的校准件,这些校准件可插入到夹具末端,使得测量时消除夹具的影响,此类典型的方法有SOLT、TRL等[4−5]。第二类方法为数学运算,先分别获得整体的S 参数和夹具的S 参数,然后通过数学方法去除夹具S 参数,最后得到去嵌后的DUT 的S 参数。此类典型的算法包含AFR、Delta L 等[6−7]。第一类方法可有效地去除夹具的影响,但是需要针对不同器件、连接器设计制作不同的校准件进行测试,这一过程复杂且效率低下。而第二类方法能够简便并且精确地进行去嵌工作,是目前业界多数使用的S 参数去嵌方法[8]。
Delta L 算法是由Intel 提出的,该算法通过设计两条长短不一的传输线,分别测出两条传输线的插入损耗值,将插入损耗进行差值计算,从而获得DUT 的插损。该算法对长短线的设计有线差需大于3 inch 的要求,否则会由于存在的多重反射影响实验结果。该算法目前认为可适用于信号频率为15 GHz 以内的高频信号。AFR 是内嵌在矢量网络分析仪(VNA)中的一个算法。首先对夹具S 参数进行分解,得到夹具A 和夹具B 的S参数,接着从“夹具+DUT”的S 参数中去除夹具A 和夹具B 从而得到DUT 的S 参数。AFR 算法只能适用于频率为10 GHz 以内的信号,无法分析再高频的信号。而且由于内嵌在VNA 中只能一次运行得一个结果,测试效率低下。
本文设计了一种先分解后去嵌的算法,可独立于仪器并应用于高频信号。算法利用时域测量来进行夹具的分解,采用ABCD 矩阵运算去除分解后的夹具S 参数,从而得到DUT 的S 参数。实验结果表明该算法能够分析频率大于15 GHz 的高频信号,并且该算法在输入端和输出端夹具不一致情况下也可工作。
2 算法实现
2.1 S 参数的分解
为了消除夹具的影响,需要对夹具参数进行去除。本文算法假设测试使用的是对称夹具,图1 显示了二端口网络中,夹具为一条均匀传输线,可分解为夹具A 和夹具B,用S 参数来表示二端口网络的信号流程。

图1 二端口网络的信号流程图
由图1 中三个S 参数的信号流程关系图可以得到:

式中,S11、S12、S21 和S22 为整体夹具的S 参数,都通过VNA 测试得到。S11A、S12A、S21A、S22A为分解得到的左夹具A 的S 参数,S11B、S12B、S21B、S22B为分解得到的右夹具B 的S 参数,这些为所要求的参数。夹具移除的第一步是得到夹具的时域响应。为了得到最佳的时域分辨率,需在较宽的频带范围内对夹具进行测量。如图2所示,得到S12 的阶跃响应T21,T21 的最大值处为夹具的1/2 时延,因为通常所设计夹具为对称,所以将T21 的最大值视为夹具的中心。通过傅里叶逆变换将频域参数S11 变为时域参数T11,设T21 的最大值为T11 的中心点,利用窗函数从T11 的中心点处截断,得到S11A的时域。接着再进行傅里叶逆变换得到S11A的频域。同理可获得S11B。由于是对称夹具,因此S12A=S21A=S12B=S21B。结合这些已知条件,最后可计算得到所有的未知数,将S11A、S12A、S21A和S22A结合得到夹具A 的S 参数,将S11B、S12B、S21B和S22B结合得到夹具B 的S参数。图3 为算法的具体流程图。
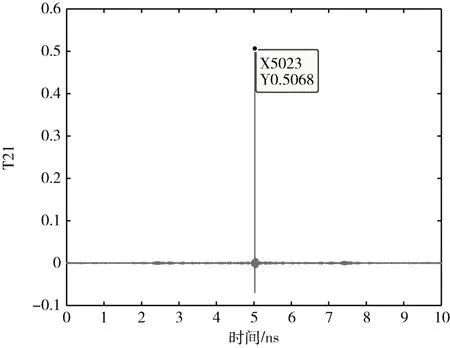
图2 夹具的时域响应

图3 二端口S 参数分解算法的具体流程图
对于高频电路,高速信号都是走一对的差分线,多数情况下所用夹具为四端口网络。首先将S 参数的单端模式转换为差分模式,得到SDD、SCD、SDC 和SCC。其中SCD 和SDC 为差模与共模的转换,而在理想的差分对中认为共模的能量为0,所以可以设SCD 和SDC 为理想的0 值。接着将SDD 和SCC 差模转差模,共模转共模这两个参数分别用上述的二端口S 参数分解算法进行分解。接着将SDD 的S11、S12、S21、S22 作为新生成的夹具A 的SDD。而SCC 的S11、S12、S21、S22 作为新生成的夹具A 的SCC。这样就可以得到夹具A 的差分S参数。同理可得夹具B 的差分S 参数。
2.2 S 参数的去嵌
将分解后的夹具A、夹具B 的S 参数与测量得到的整体的待去嵌S 参数进行数学处理计算,得到去嵌后的DUT 参数。对于一个二端口网络,转移矩阵(ABCD 矩阵)可由S 参数转换而来,常用于无源器件的分析。
ABCD 矩阵参数与S 参数的关系如下:

式中,A、B、C、D是传输参数,A为电压传输函数,B为转移阻抗,C为转移导纳,D为电流传输函数。S11、S12、S21、S22 为二端口网络的S 参数,Z0为阻抗的复数形式。
整个待去嵌的S 参数,可视为夹具A、DUT 以及夹具B 级联的结果。对于二端口网络的级联,上个网络的输出电压和电流是下个网络的输入电压和电流,如图4所示。

图4 三个二端口网络的级联
夹具A、夹具B 和DUT 的ABCD 矩阵级联,可得到DUT 的ABCD 矩阵:

四端口网络的S 参数包含16 个参数,将这16 个参数进行四四划分,重新形成二端口S 参数的模式。其中S11、S12、S12、S22 作为一个 新的S11,S13、S14、S23、S24 作为一个新的S12,S31、S32、S41、S42 作为一个新的S21,S33、S34、S43、S44 作为一个新的S22。这新生成的参数可作为式(5)~式(8)中的S11、S12、S21 和S22。而新生成的S11、S12、S21 和S22 都各自为一个2 × 2 的矩阵,所以将式(5)~式(8)中的1 转换成2 × 2 的单位矩阵,最后可得到四端口网络的ABCD 矩阵。接着将ABCD 矩阵通过数学运算变换为S 参数,则得到去嵌后的DUT 的四端口S 参数。
3 实验结果与分析
3.1 测试板设计
设计了十八层测试板,长线线长设计为9 inch,短线线长设计为1 inch。每层设计不一样的PP 和core 厚度,增加实验的多样性。影响走线层插入损耗的参数的详细信息如表1。

表1 测试板走线层基本信息
使用VNA 进行S 参数的测量,测量频率设置为100 MHz 到30 GHz,得到9 对9 inch 长和1 inch 长的四端口网络S 参数。各组参数分别测试三次,对测试结果进行AFR 去嵌、Delta L 去嵌和本文算法的去嵌。最后将去嵌后的S 参数进行插损的统计,将同一组里的三条插损进行平均求平均值。
3.2 S 参数的分解测试
为验证本文算法对四端口网络的分解能力,将测试板各层的夹具插损结果进行对比。分别做出分解后的夹具A 和夹具B 以及整体夹具的插损曲线图,读取15 GHz频点下的损耗值。
图5 显示了分解后的夹具A 和夹具B 以及整体夹具的插损对比,可以看到,八种叠层结构下算法分解后的夹具A 和夹具B 的插损曲线几乎重合。在表2 中看到八种叠层结构下在15 GHz 频点时夹具A 和夹具B 的插损差值不超过0.01 dB,说明算法可以平均的分解出夹具A和夹具B。通过求出夹具A 与夹具B 的插损之和与整体夹具的插损进行数学减,发现最大差为0.07 dB。说明本文算法能够准确并且平均的将整体夹具的S 参数分解得到夹具A 和夹具B 的S 参数。

表2 15 GHz 下夹具插损对比(dB/inch)

图5 夹具A、夹具B 以及整体夹具在各层中的插损对比
同时可以看到在L3、L14 和L16 中由于原始夹具参数的抖动较大,导致分解后的曲线在20 GHz 往后有所抖动。而在L9、L18 中的原始测试数据较好,分解后的曲线平滑度较好。说明该算法对测试数据有一定的要求,若测试数据不够准确会导致20 GHz 往后的分解数据不够准确。
3.3 S 参数的去嵌测试
接着将得到的分解后的夹具A 和夹具B 的S 参数与9 inch 线长测量得到的S 参数进行去嵌处理,得到DUT的S 参数。将本文算法分别与Delta L 算法、AFR 方法做对比。
由图6 可看到,本文算法与Delta L、AFR 在各层中的插损曲线在10 GHz 之前基本完全重合。而业内普遍认为AFR 算法能够精确地去嵌10 GHz 以内的信号。说明这三种算法都可以用来去嵌频率在10 GHz 内的信号。在10 GHz 之后,AFR 方法与其他两种相比逐渐开始抖动,并且随着频率的升高,抖动变大。在15 GHz 往后,AFR 方法已由于抖动过大而不可应用,所以AFR 方法不适用于高频信号的去嵌。而在L3、L5、L9、L12、L16 和L18 中,本文算法与Delta L 在频率15 GHz 以内基本重合。而Delta L 算法能够应用在速率为15 GHz 的信号,说明本文算法对15 GHz 以内的信号去嵌没有问题。在15 GHz 之后,明显本文算法的抖动性小于Delta L 算法,并且可以发现在L5、L9、L18 中,本文算法在30 GHz 都没有出现抖动,说明如果在夹具和待测器件设计得很好,测量误差很小的情况下,本文算法可以用于更高频信号的去嵌。

图6 三种算法在各层中的插损对比
Delta L 算法对线差有要求,线差过小的话,会由于反射存在造成波形抖动。虽然该测试实验的线差为8 inch,但是依然可以看到某些情况下,如在L14 和L16中,Delta L 算法从低频开始就有点抖动。说明Delta L算法对原始测试数据质量的要求高于本文算法。总体来说,与AFR 去嵌方法相比,本文算法能够实现更高频信号的去嵌。并且由于不内嵌入于VNA 中,在编码中加入了批量运算,解决了AFR 单次去嵌运算效率低下的问题。与Delta L 去嵌算法相比,本文算法对线差长短没有要求,而且可工作于左右夹具不一致的情况,使得本文算法可应用于更多的实际测试场景。
4 结论
本文设计了可用于四端口网络的高频S 参数去嵌算法。该算法首先设计了一种基于时域的S 参数分解方法。接着利用ABCD 矩阵进行数学运算得到去嵌后的S参数。设计了十八层的测试板,将本文算法与AFR 方法和Delta L 算法进行对比,验证了本文算法对高频信号去嵌的准确性和有效性。同时由于先分解后去嵌的设计,使得本文算法可应用于左右夹具不一致的情况。最后在算法代码中加入了批量运算,提高了测试效率。
