光纤光栅与人工智能融合的形状自感知穿刺针

李天梁，宋珍珍，陈发银，苏轶飞，谭跃刚

（武汉理工大学 机电工程学院，湖北 武汉 430070）

1 引言

近年来，中国已是世界范围内癌症发病率增幅最大的国家之一，而例行筛查和早诊早治可大大降低恶性肿瘤患者的死亡风险，已成为肿瘤预防的有效途径［1-2］。在临床诊断过程中，仅仅通过影像学检查难以对病灶定性，活体组织的病理检查才是诊断的金标准［3］。但传统的穿刺活检手术过程中穿刺针因与人体组织的交互作用会产生微量弯曲，从而导致穿刺针不能准确到达靶区或进针过程中损伤人体重要组织，穿刺精度与诊疗效果严重依赖医生的经验［4］。手术机器人因为可以术前精确规划路径避免重要人体组织损伤以及有较高的操作精度而被广泛应用于穿刺活检手术之中［5］。但现阶段手术机器人进行穿刺手术主要依赖于医学图像和导航技术，主要有超声成像、计算机断层扫描（Computed Tomography，CT）以及磁共振成像（Magnetic Resonance Imaging，MRI）。但上述技术手段存在着以下不足：超声成像在人体组织中对比度较差，小肿瘤几乎不可见，CT 成像会使医生长时间暴露于辐射下，严重影响医护人员健康，MRI 扫描仪内部器件的工作精度会受到扫描仪强电磁干扰的影响［6-7］。目前针对刚性穿刺针的穿刺力、柔性穿刺针的针体形状准确实时获得不足，无法实现穿刺过程的信息感知以及精准的靶点操作［8］。因此发展一种高精度、小型化且抗电磁干扰的穿刺针力形状感知方法，为手术机器人辅助穿刺提供实时、准确的形状信息，对于提高穿刺手术的安全性与准确性有着重大意义［9］。

近年来，光纤传感器因具有抗电磁干扰、良好的生物兼容性和微型化尺寸等优势而引起国内外学者的广泛关注。它能克服电类敏感元件的大部分局限，实现狭小空间下手术器械变形的精准测量［10-11］。Li 等人［12］设计了一种带有三光纤共三组光纤光栅（Fiber Bragg Grating，FBG）的穿刺针传感器，并对得到的离散曲率数据用四阶多项式进行拟合得到穿刺针整体形状。Jin 等人［13］提出了通过穿刺针内的三根光纤上的FBG传感器获得曲率测量数据，并基于弹性杆理论和李群理论进行穿刺针的形状重构。Khan.F等［14］利用刻有FBG 的多芯光纤制作传感器来测量多段导管的姿态，并基于布拉格光栅的测量值转换为应变，再根据应变数据推导出曲率，最后利用曲率和Bishop 框架方程重构导管姿态。Zhang等［15］利用三光纤五组光纤光栅实现210 mm 长穿刺针的二维形状重构。但是文章所提出的重构算法的形状数据均是基于传感器的标定转换矩阵由FBG 的波长数据得到穿刺针的离散位置信息，而后对位置信息进行多项式拟合得到形状的数学表达，数据处理过程繁杂。另外多项式拟合的次数越高，其对关键节点位置信息的准确度就要求越高，否则任何位置的信息偏差都会导致重建结果的巨大变化［16］，所以上述重构方法不适合复杂变形重构。

为了解决上述问题，本文提出了一种融合分布式FBG 传感技术和人工智能的形状自感知穿刺针。基于形状自感知穿刺针弯曲变形与光纤光栅中心波长变化之间的映射关系，分别搭建了形状自感知穿刺针的形状标定实验装置与其动态性能测试试验装置，得到不同弯曲状态下光纤光栅的中心波长数据与利用canny 边缘检测算子提取得到的穿刺针实验图片序列形状曲线数据。融合反向传播神经网络（Back Propagation neural network，BP），得到光纤光栅中心波长漂移量与形状函数之间的映射模型，实现了形状自感知穿刺针的三维形状重构。实验结果表明：穿刺针针体的形状重构误差值可达到0.90 mm 以内，弯曲方向角的最大误差为5.03°；在动态性能验证实验中，形状重构最大误差值为0.84 mm，弯曲方向角的最大误差为1.02°。因此，该光纤传感方案与形状重构算法在穿刺针形状实行精准感知与调控方面具有广阔的应用前景。

2 形状自感知穿刺针传感结构

形状自感知穿刺针由镍钛合金穿刺针基体、3 根分别刻有5 个FBG 的单模石英光纤构成，其结构尺寸与FBG 布置情况如图1 所示。穿刺针基体悬置长度为150 mm，直径为3 mm，沿其轴向刻有3 个间隔120°、深0.4 mm 的直角型凹槽。3 根直径为125 μm 的单模石英光纤分别命名为Fiberi，（i=1，2，3），通过环氧树脂胶粘贴在镍钛合金穿刺针基体上的凹槽中。每根光纤上的5 个FBG 栅区长度均为3 mm，相邻FBG 中心间隔28 mm，从穿刺针尖端至尾端分别命名为FBG_ij，（j=1，2，3，4，5），初始波长依次分别为1 535 nm，1 540 nm，1 545 nm，1 550 nm，1 555 nm，穿刺针同一横截面上的3 个FBG 作为一组传感单元，共构成5 组传感单元。

图1 形状自感知穿刺针结构Fig.1 Structure of shape self-sensing needle

3 基于BP 神经网络的形状重构算法

3.1 FBG 的传感原理

根据耦合模理论，FBG 中心波长λB取决于其周期Λ和有效折射率neff，任何使这两个参量发生改变的物理量，都会引起FBG 中心波长发生漂移：

穿刺针与组织交互时发生形变，带动其表面的FBG 产生轴向应变，进而引起FBG 中心波长的漂移。设FBG 初始中心波长为λB，当FBG 受到轴向应变时εi，其中心波长漂移Δλ 可表示为：

其中，pe为有效弹光系数。

穿刺针在进针过程中受到的轴向载荷更大，而非受到集中载荷，假设变形曲线C可采用三次多项式简化为：

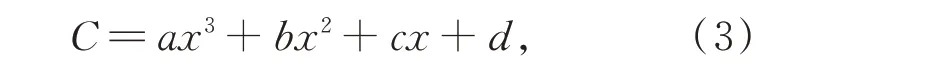
其中，a，b，c，d分别为该三次多项式的各项系数值。通过文献［12］可知，穿刺针形状曲线C与FBG 中心波长漂移量Δλ 之间存在非线性的映射关系。BP 神经网络是一种按误差反向传播算法训练的多层前馈网络，能学习和存贮大量的输入—输出的映射关系，无需训练前揭示描述映射关系的数学模型，在解决非线性回归问题上应用广泛［17］，而且调用建立的模型可快速实现形状重构输出，所以本次采用BP 神经网络算法重构穿刺针形状。

3.2 传感器形状感知标定实验系统

为了获取训练神经网络模型所需的数据，设计并搭建了形状自感知穿刺针静态标定实验系统，如图2 所示。首先通过3D 打印制备的连接件将形状自感知穿刺针固定在RS60 旋转微调架上，实现穿刺针的定位，然后通过Z方向微调架安装在试验台上。根据穿刺针小变形假设，设计并通过3D 打印技术制备了5 个曲率标定板，曲率值依次为 0.000 0 mm-1，0.000 2 mm-1，0.000 4 mm-1，0.000 6 mm-1和0.000 8 mm-1。采用光纤光栅解调仪（高斯光学有限公司，中国；型号：OPM-T1620；采样率：105 Hz；分辨率：1 pm）作为接收FBG 反射光谱信息的装置。

图2 形状感知标定实验装置Fig.2 Shape sensing calibration experimental device

通过Labview 编程在PC 端显示并记录形状自感知穿刺针上15 个FBG 的中心波长数据。首先记录15 个FBG 的初始中心波长数据，而后将形状自感知穿刺针固定在曲率标定板的凹槽中，记录所有FBG 的中心波长，调节RS60 旋转微调架调整穿刺针的安装角度θ，每次实验角度间隔为10°，角度调节范围为0～360°。进行了5 次实验，共测得180 组数据，以其中157 组作为神经网络模型的训练数据，33 组作为测试数据。

如图3 所示，显示了θ=0°时3 根光纤在5 种不同曲率下的光谱数据，为了更直观地分析光谱变化趋势，对原始光谱进行了滤波和归一化处理。图3（a）显示的是Fiber 1 的反射光谱，理论上该实验条件下，Fiber 1 处于穿刺针中性层上，不会出现波长漂移现象，但是由于传感器的制备与安装误差，导致在实验过程中其产生了微量波长漂移；图3（b）和图3（c）分别是Fiber 2 和Fiber 3在5 种不同曲率下的光谱数据，实验时两者受力方向相反，所以两者的波长变化趋势相反，Fiber 2 光谱整体右移，Fiber 3 光谱整体左移，随着曲率的增加，光谱移动的幅度也越大。另外可以看到，在同一曲率板作用下，FBG 的初始中心波长越大，产生波长漂移量也越大。这是因为同一光纤上沿穿刺针轴向曲率是相同，通过式（2）也可以推导出相同的结论。

图3 3 根光纤在5 种曲率下的反射光谱Fig.3 Reflection spectra of three fibers under different curvatures

3.3 基于BP 神经网络的穿刺针形状重构算法

将标定实验所得波长数据及形状数据划分为训练样本和测试样本，训练样本用于训练神经网络得到满足设定迭代次数的模型参数，构建神经网络预测模型。调用该模型对测试样本进行预测，预测结果用来评价该模型。通过仿真调试，综合考虑模型训练时间和预测精度，最终确定的神经网络模型结构如图4 所示，包括1 个输入层，2 个隐藏层，1 个输出层。其中以形状自感知穿刺针上5 组传感单元中心波长漂移量Δλ作为输入层输入数据，该层有15 个神经元节点；第一隐含层和第二隐含层神经元节点数分别为31和10；输出层包含5 个节点，即穿刺针变形曲线的多项式各项系数值及穿刺针变形平面与x-y平面的夹角θ。此外，激活函数、学习函数也是BP神经网络模型的重要组成部分，本次神经网络模型隐藏层、输出层的激活函数均采用双极性S函数（tansig），学习函数选取梯度下降的权值/阈值学习函数（learngdm）。

图4 基于BP 神经网络的穿刺针形状重构算法Fig.4 Needle Shape reconstruction algorithm based on BP neutral network

输入信号Δλ经第一隐含层后的输出p1可以表示为：

p1经相邻的第二隐含层后的输出p2可表示为：

p2经相邻的第二隐含层后的输出u可表示为：

其中：w1，w2，w3分别为输入层与第一隐含层、第一隐含层与第二隐含层、第二隐含层与输出层之间的权值系数，两个隐含层的权值系数，b1，b2，b3分别为其对应的偏置。

激活函数f（）采用tansig 函数：

本次针对穿刺针平面变形进行测量，重构误差分为穿刺针形状曲线C上针尖处的绝对误差和弯 曲方向角θ的绝对误差［18］。上述33 组测 试样本的两类误差如图5 所示，形状误差最大值为0.90 mm，弯曲方向角最大误差为5.03°。

图5 测试样本误差Fig.5 Error of test set sample

4 形状自感知穿刺针形状测量与重构

4.1 融合图像处理技术的形状重构性能测试系统

为验证上述神经网络模型的性能，设计搭建了融合图像处理技术的动态形状重构性能测试系统。采用单目摄像机（索尼（中国）有限公司；型号：α7000；分辨率：3 840×2 160）记录实验过程穿刺针的整体形态，采用光纤光栅解调仪作为接收FBG 反射光谱信息的装置。形状自感知穿刺针通过3D 打印零件与X-Y方向微调架连接，调整微调架可对穿刺针针尖处施加偏移量。为验证穿刺针的动态响应性能，调整微调架以锯齿波的变化趋势变幅值施加位移，利用FBG 波长数据采集系统和摄像机分别记录实验过程中的FBG 波长和穿刺针的形状信息，实验装置如图6所示。

图6 形状自感知穿刺针动态测试实验装置Fig.6 Shape self-sensing needle dynamic test experimental setup

其中摄像机获得的实验视频文件通过图像识别算法可得到穿刺针的形状数学表达。首先将视频文件导入到MATLAB 中，实现视频的分帧，得到每帧的实验图像；通过定区域剪裁去除部分背景，仅保留穿刺针所在的区域，以避免背景对下一步边界识别的干扰，得到更准确的边界曲线。由于实验过程中照明情况不佳，导致穿刺针针体与背景（试验台）区分度较小，而canny 算子可充分考虑图像梯度，具有较好的连续性和较准确的定位［19］，故选择了该算子。

调用MATLAB 中edge函数，设 定canny 算子低阈值为0.1，高阈值为0.2，得到实验图片序列的穿刺针边界，通过三阶多项式拟合可得穿刺针变形曲线，具体算法流程如图7 所示。

图7 基于canny 算法的穿刺针形状提取Fig.7 Edge extraction of needle shape based on canny edge detection algorithm

4.2 形状自感知穿刺针重构误差分析

图8 经神经网络预测输出的形状重构结果Fig.8 Shape reconstruction result by the neural network

图8（a）是动态性能测试实验过程中穿刺针形状重构曲线与摄像机捕获的实际形状曲线上针尖的偏移量。图8（b）是取图8（a）中一段波谷（139 s）至波峰（167 s）段显示神经网络模型预测输出的穿刺针空间形状。图8（c）分别显示了动态性能测试实验的形状曲线误差和弯曲方向角误差，形状曲线C最大误差为0.84 mm，弯曲方向角θ最大误差为1.02°。动态实验结果说明所提出的神经网络算法可以实现实时的形状输出。

5 结论

本文提出了一种基于分布式FBG 传感原理的穿刺针形状感知传感器结构和封装方法，构建了穿刺针变形重构的神经网络模型，用以监测穿刺针的微量变形。通过实验研究和数值分析，验证了所设计的形状自感知穿刺针可感知穿刺针微量弯曲变形、弯曲方向角，分析得到针尖处重构相对误差小于0.90 mm，弯曲方向角最大误差为5.03°。在动态性能测试实验中，针尖处重构相对误差小于0.84 mm，弯曲方向角最大误差为1.02°，神经网络模型的运行时间也可满足手术过程中穿刺针位置实时显示的要求。综上所述，所提出的形状自感知穿刺针及其形状重构算法能够实现穿刺针微量变形的测量，在机器人辅助/自主穿刺方面具有潜在的应用价值。但设计训练得到的神经网络模型鲁棒性还有待提高，理论上通过增加训练样本数据可以得到精度更高、鲁棒性更强的神经网络模型。