随机二阶锥互补约束优化模型的一般光滑化SAA方法

王博, 初丽

(1. 福州大学数学与统计学院，福建 福州 350108； 2. 福建工程学院计算机科学与数学学院，福建 福州 350118)

0 引言

本研究分析一类较为一般的含有二阶锥互补约束(SSOCMPCC)的随机优化模型:

min{E[f(z,ξ(ω))]|KmE[G(z,ξ(ω))]⊥E[H(z,ξ(ω))]∈Km}

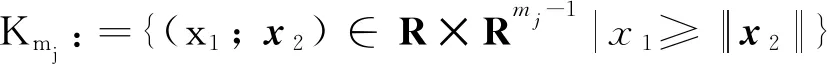
SSOCMPCC模型是有实际意义的. 其中随机变量的引入可以源于数据的误差和未来的不确定性； 互补约束可以来自于逆问题[1-2]或双层规划问题[3]的转化.

SSOCMPCC模型在所有二阶锥维数都为1(即m1=m2=…=mn=1)时，退化为随机互补模型(SMPCC):

min{E[f(z,ξ(ω))]|0≤E[G(z,ξ)]⊥E[H(z,ξ)]≥0}

关于相对简单的随机互补模型的理论研究和求解方法，可参考相关文献[4-7]. 需要指出，SSOCMPCC模型并非SMPCC模型的平凡推广. SSOCMPCC模型可行集合不再有多面体性质，其一阶必要性条件更为复杂. 稳定性理论可参考Zhang等[8]、 Liang等[9]和Ye等[3]的工作. 需要注意关于C稳定点的定义是有歧义的，具体可以参见Chu等[10]的工作.

本研究希望构造一个求解SSOCMPCC模型的不依赖具体光滑化函数的光滑化SAA方法的一般框架. 该框架的构造对SSOCMPCC模型有效算法的研究具有积极作用.

假设E[f(z,ξ(ω))]、E[G(z,ξ(ω))]和E[H(z,ξ(ω))]对所有的z∈Rm都是有定义的.ξ(ω)简记为ξ.对应于锥Km，映射G(z,ξ)和H(z,ξ)可以进行如下分块，即：

假设可以抽样得到随机向量ξ的N个独立同分布的样本ξ1,ξ2, …,ξN.由此可构造SSOCMPCC模型的近似问题:

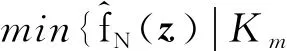
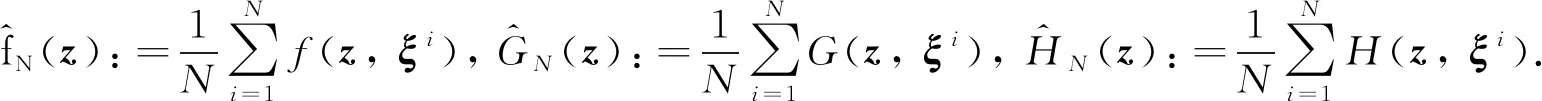
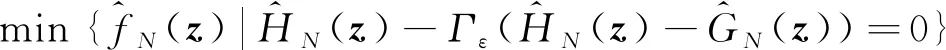
(1)

问题(1)依赖于ε的解z(ε)是随机变量.期望当ε→0时，z(ε)在某种概率意义下能接近SSOCMPCC模型的解.若Γε(·)为CHKS 光滑化函数时，由文献[10]知，上述期望是成立的.后续讨论将指出较一般的一类光滑化函数也有类似的性质.

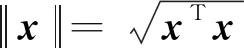
1 预备知识

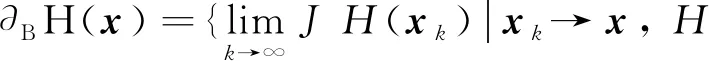
给定x=(x1;x2)∈Rt，在二阶锥Kt意义下的谱分解为：

x=λ1(x)c1(x)+λ2(x)c2(x)

(2)

其中:i=1, 2,λi(x)和ci(x)分别为x的特征值与特征向量，即：

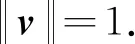
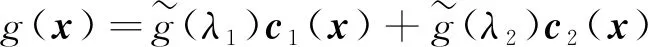
(3)

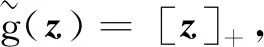
SK(x)=[λ1(x)]+c1(x)+[λ2(x)]+c2(x)

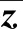
SSOCMPCC模型的拉格朗日函数可定义为：

计算可得其关于z的梯度为：

为了建立收敛性理论，还需要如下约束规范成立：

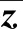
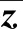
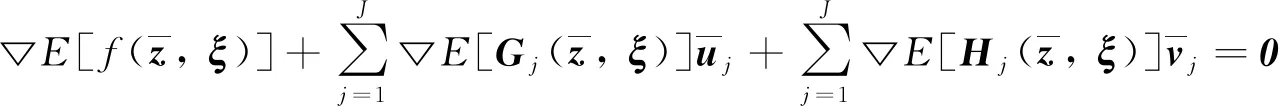
(4)

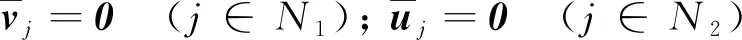
(5)

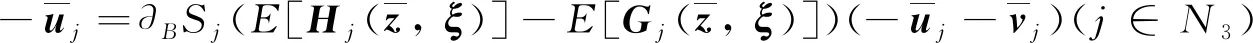
(6)

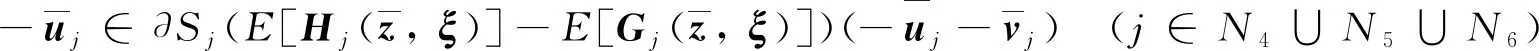
(7)

注意C稳定性强于弱稳定性[10]. 稳定性定义中需要计算投影算子Sj的B次微分的具体形式. 此处可利用Zhang等[8]文献中的引理2.1. 而广义雅克比可由公式∂Sj=conv∂BSj得到.

接下来的讨论需要假设随机向量ξ的样本ξ1, …,ξN是独立同分布的，且满足下述条件.

条件1映射f(·,ξ)、G(·,ξ)和H(·,ξ)在Rm上对几乎所有的ξ∈Ξ都二阶连续可微.

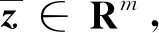
由条件1和条件2可知，E[f(z,ξ)]、E[G(z,ξ)]和E[H(z,ξ)]是二阶连续可微的(参见文献[4]定理7.44).根据大数定律，如下引理成立(参见文献[4]定理 7.48).

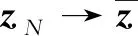
2 SSOCMPCC问题的光滑化SAA方法

求解问题(1)时，需要选择适当的光滑化映射Γε(·). 本研究中光滑化映射的构建基于 Fukushima等[13]研究的如下一类光滑化函数.

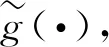
满足条件3的光滑化函数具有非常良好的性质.

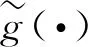
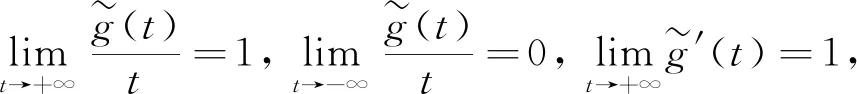
引理3设ψε(·)为如上定义的映射，则有：Jψε(x)是正定的，且I-Jψε(x)可逆.

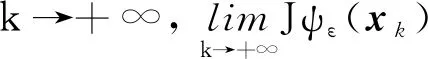
接下来讨论收敛性. 下述结果是文献[10]中引理3.2的推广.

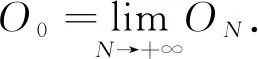
证明 给定正数εN和任意固定向量ω=(ω1; …;ωJ)∈Rm，设其谱分解为：

可以按下述方式构造(αN,βN)：

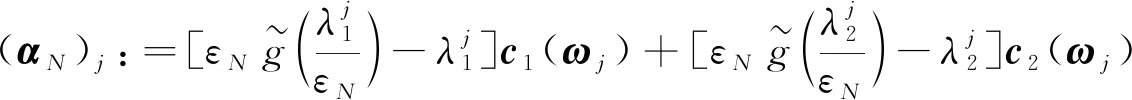
(8)

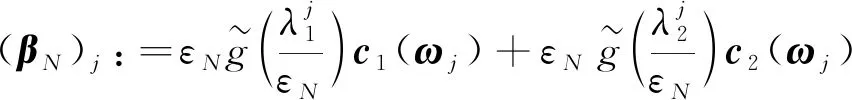
(9)

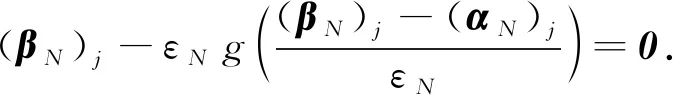
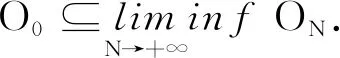
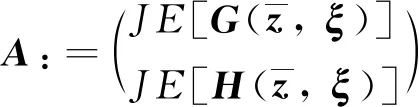
上述命题证明方式类似于文献[10]中的命题1. 受篇幅所限，具体证明过程略去. 此结果总结了SSOCMPCC模型和问题(1)之间可行集的关系. 接下来的定理描述了其解之间的收敛性关系.

SSOCMPCC模型可以通过序列问题(1)近似. 具体的近似关系，可由如下结论刻画.

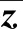
上述结论可以利用专著[14]中的定理7.31简单得到，此处不再赘述.

实践中最优解几乎无法取得，接下来的讨论总结了SSOCMPCC模型与问题(1)稳定点之间的关系. 较之于最优解间的关系，此类似结论更实用.

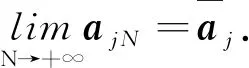
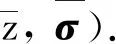
证明 KKT对(zN,σN)满足：

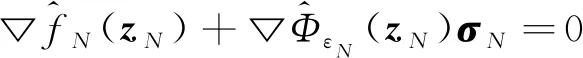
(10)

设

则简单验证可得：

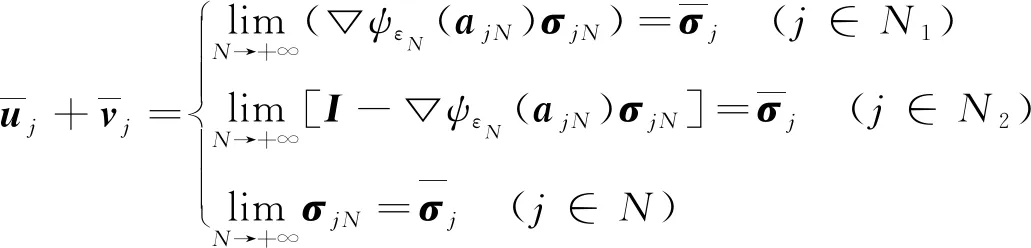
(11)

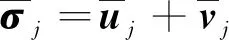
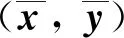
由上述定理的证明过程稍加修改，不难证明在更强的假设下有如下结论成立：

基于上述分析，可得求解SSOCMPCC模型的一般光滑化SAA算法框架如下：

算法 一般光滑化SAA算法框架取N为充分大的整数, g (·)为适当的光滑化函数. 步骤1 令εN=10-N. 取随机向量ξ的N个独立同分布样本, 记为ξi, i=1, 2, …, N. 步骤2 求解SAA子问题min{f^N(z)Φ^εN(z)=0}得到稳定点zN. 步骤3 若满足终止条件则终止迭代; 否则增大N并转步1.

实际执行算法时，需要提前确定终止条件. 注意由于本研究讨论的是数学期望没有显示表达式的情况，确定已得到的向量是否是解是几乎不可能的. 具体的终止条件可取两次迭代之间的差别足够小，也可以在N充分大时终止.

3 应用

本研究提出的一般性框架可以视为基于特殊光滑化函数的光滑化方法的推广. 光滑化函数可分别取CHKS函数[15-17]和S形函数1/(1+e-x)的积分:

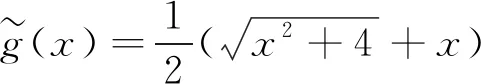
(12)

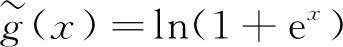
(13)

根据本研究的结论，易得如下收敛性结论：

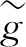
光滑化函数取为式(12)时，该结论和文献[10]中给出的一致. 若加强假设条件，则可以保证收敛到更强的M稳定点[10]. 光滑化函数取为式(13)时，得到的具体算法较为新颖. 上述结论保证了算法基本的收敛性.

4 结论

提出一种求解SSOCMPCC问题的一般光滑化SAA方法框架. 本框架中，只要选取的光滑化函数满足Fukushima等[13]提出的条件，在适当的假设下，就可以保证子问题的稳定点以概率1收敛到SSOCMPCC的C稳定点. 本研究给出了两个具体的光滑化函数并讨论了对应的收敛性结论，由此验证框架的实用性.