基于相干多普勒激光雷达的斜程湍流参数反演方法研究

陈晓敏 , 张洪玮 , 孙康闻 , 吴松华 ,2*

( 1 中国海洋大学信息科学与工程学部海洋技术学院, 山东 青岛 266100;2 青岛海洋科学与技术试点国家实验室, 区域海洋动力学与数值模拟功能实验室, 山东 青岛 266237 )

0 引 言

大气湍流作为大气中一种广泛存在的运动形式, 具有尺度覆盖范围大、变化速度快的特点。大气湍流对航空安全的影响不可忽视[1], 起飞或降落轨迹上的湍流 (斜程湍流) 会导致飞机颠簸, 严重的会造成飞机失控, 引发重大安全事故。飞机起飞或降落轨迹上大气湍流的准确探测, 不仅能够降低由大气湍流导致的飞机事故率, 而且对于提高机场运行效率和研究不同空间位置的大气湍流特征具有积极意义。

高时空分辨率和高精度的风场数据是低空斜程湍流反演的基础。传统的超声风速计安放高度通常为10 m, 有限的探测高度限制了其在斜程湍流探测中的应用[2];天气雷达是航空气象保障中重要的气象观测设备, 在湿度较大的天气下可以发挥作用, 但天气雷达空间分辨率差、数据刷新率低且在晴空无云的天气情况下探测能力不足[3]; 风廓线雷达只能够获得其所在位置上方的风廓线, 无法获取较大范围内的风场情况, 因此无法获得飞机起降轨迹上的风场数据[4]。近年来, 相干多普勒测风激光雷达凭借时空分辨率高、轻便、扫描模式多样等特点成为晴空条件下航空气象保障的可靠设备。相干多普勒测风激光雷达能够根据不同观测需求设置不同的扫描模式, 进而获取低空风场。

针对不同扫描模式采用对应的速度结构函数法反演大气湍流参数是相干激光雷达观测大气湍流的难点和关键。近年来, 相关研究已陆续开展。2002年, Frehlich和Cornman[5]利用相干多普勒激光雷达模拟数据的径向速度估计获取了模拟湍流速度场的空间统计特性, 并利用径向速度计算得到的结构函数计算出湍能耗散率ε和积分尺度。2005年, Smalikho等[6]、Frehlich等[7]利用脉冲相干激光雷达距离-高度-显示 (RHI) 扫描模式的观测结果从多普勒谱宽与高度结构函数两个方向反演大气湍流参数, 并对实验结果采用数值模拟, 证实了这两种方法的可靠性。2008年, Frehlich[8]采用固定俯仰角、改变方位角的平面-位置-显示 (PPI) 扫描模式, 使用纵向结构函数方法和横向结构函数方法反演边界层内的湍流参数, 并将反演结果同超声风速计的探测结果进行了对比, 数据的一致性较好。2011年, Chan和Lee[9]对PPI扫描径向风场数据进行子扇区划分, 使用速度结构函数计算得到每个子扇区内的ε1/3, 进而获取了ε1/3的空间分布情况。2017 年, Smalikho 和Banakh[10]使用速度-方位-显示 (VAD) 扫描模式下的方位角结构函数反演大气湍流参数, 并将该方法的适用范围由对流边界层扩展到稳定边界层。2017至2019年, 中国海洋大学翟晓春等[11,12]采用VAD、PPI和RHI等多种激光雷达观测模式研究了大气边界层内的湍流垂直结构特征, 分析了不同粗糙度下垫面影响下的风机尾流与大气湍流的相互作用特点, 并且探究了大气湍流对飞机尾涡演化过程的影响。

而针对飞机起降轨迹上的斜程湍流, 香港天文台开展了一系列飞机下滑道区域内的湍流观测研究。2007年, Kwong和Chan[13]证明了相干多普勒测风激光雷达能够在近实时的情况下生成沿飞机滑行路径的ε剖面。2010 年, Chan[14]利用方位角结构函数和速度结构函数进行了下滑道上的低空湍流反演与预警, 获取了ε, 两种计算方法的结果一致, 并与飞行数据以及风切变与湍流预警系统 (WTWS) 的结果一致。2014年,Hon和Chan[15]将速度结构函数法应用到针对飞机起降阶段沿滑行路径区域扫描的下滑道扫描模式, 获得了沿滑行路径的ε1/3剖面, 与飞机的飞行员报告匹配较好。2010年, Chan[14]利用方位角结构函数和速度结构函数进行了下滑道上的低空湍流反演与预警, 获取了ε, 两种计算方法的结果一致, 并与飞行数据和风切变与湍流预警系统 (WTWS) 结果一致。然而对于斜程空间范围内的湍流参数反演研究依旧处于起步阶段, 同时缺乏对于斜程空间湍流的连续观测。

本文利用安放于某机场的相干多普勒测风激光雷达, 获取下滑道扫描模式下的高时空分辨率风场数据,将获取的径向风速数据进行5°方位角和60 m距离的扇区划分, 进一步基于Kolmogorov局地均匀各向同性湍流理论, 并使用横向结构函数法估算斜程湍流的ε1/3分布情况。具体分析了某机场南段跑道2018年12月15日凌晨 01:38―01:50 以及 02:22―02:35 两个时间段的观测数据, 获得的ε1/3斜程空间分布情况。最后, 在同区域、同时段内, 使用相同数据计算了与ε1/3相同量纲的风切变强度, 并将二者进行了对比验证。

1 理论方法

大气湍流在产生、发展和消散的过程中会形成各种尺度的湍涡, 某些小尺度湍涡具有各向同性的特性,可以进行统计模拟, 因此在实际研究中, 小尺度湍涡的研究是目前湍流研究领域的关注点。在Kolmogorov局地均匀各向同性湍流理论的假设中, 当雷诺数足够高时, 存在湍流强度仅由ε确定的惯性子区。国际民用航空组织 (ICAO) 规定, 使用ε1/3来衡量大气湍流强度: 0.3～0.5 m2/3/s为中度湍流, 大于0.5 m2/3/s为严重湍流。

速度结构函数法可利用相干多普勒激光雷达的径向风速数据估算满足Kolmogorov局地均匀各向同性理论假设下的ε值, 是当前相干多普勒激光雷达获取大气湍流ε的常用方法。该方法将由实测数据计算的速度结构函数与模型结构函数进行拟合, 获得ε值。在拟合过程中, 需要根据Kolmogorov局地均匀各向同性理论对拟合出的湍流特征尺度进行限制, 以确保其处于惯性子区内。

1.1 Kolmogorov局地均匀各向同性理论

根据Kolmogorov定律, 当雷诺数足够大时, 湍流获得充分发展。在湍涡的发展过程中, 大尺度湍涡的能量传递给次级的湍涡, 显然是各向异性的。但在串级传输的过程中, 存在一部分在统计特性上是各向同性的小尺度湍涡, 即在局地均匀各向同性区域内存在一个仅由ε确定的惯性子区, 其尺度l满足L≥l≥η, 其中L为含能尺度, 一般来说研究湍流时不考虑比含能尺度L更大的尺度;η为湍流内尺度, 最小尺度约为1 mm。在湍流的惯性子区内, 速度结构函数频谱只与ε有关[16,17]。

1.2 速度结构函数法

速度结构函数法需要对实测数据计算的速度结构函数同模型结构函数进行拟合来获取湍流参数, 在实际湍流研究中, 主要关注的是惯性子区内湍涡的贡献。速度结构函数根据数据的扩展方向分为横向结构函数和纵向结构函数两种。在本研究中激光雷达下滑道扫描模式的方位角分辨率高, 因此使用横向结构函数计算方法可以更加精确地反演大气湍流参数。横向结构函数Dv(s) 表示为

式中v′(r，θ，φ) 为实测风场减掉平均风场获得的风速脉动,r为观测点距激光雷达的距离,θ为俯仰角,φ为方位角,s为两项风速脉动之间的距离间隔。根据式 (1) 可获得基于实测数据计算的结构函数。

近地面层区域的模型结构函数可以简化表示为

式中σ2为径向风速方差, Λ(x) 为通用函数,L为含能尺度。

当L＜＜R(R表示激光光束方向距激光雷达的距离), Von Karman 模型的二维空间湍流模型为

式中q=(r2+s2)1/2,K1/3(x) 为修正的1/3阶贝塞尔函数。

当s＜＜L且满足各向均匀同性假设时, 满足Kolmogorov定理, 结构函数可以表示为

由于激光雷达光束始终存在一定的脉冲宽度, 实际测量中探测体积平均效应无法避免, 这将影响结构函数计算。Frehlich 等[7]基于上述理论推导出探测体积平均效应下的结构函数模型。

当激光雷达的横向分辨率Rsin Δφ＜＜Lv时, 则模型结构函数为

式中F(x，μ) 为高斯分布脉冲和方波窗函数下的滤波函数, 其计算公式为

式中Dmeasure(kΔs)为实测数据计算的结构函数,kΔs为结构函数距离分辨率的倍数。根据式 (10) 进行最小二乘法拟合, 即可求得湍流参数径向风速方差σ和含能尺度L, 最终通过式 (6) 求得ε。

1.3 斜程湍流反演算法

图1为斜程湍流参数反演算法流程图。使用速度结构函数法反演局地均匀各向同性假设下的斜程湍流参数, 首先需要对激光雷达获取的风速数据进行质量控制, 通过设置信噪比阈值的方法排除奇异数据。下滑道扫描模式的俯仰角与方位角同时变换, 因此获取的是空间倾斜平面上的风速数据。假设一定高度范围内的风场是均匀的, 对实测风场数据进行高度平均和时间平均获取平均风场, 进而获得风速脉动, 本研究采用15 min时间平均和2 m高度平均。图2展示了2018年12月15日01:41:17的平均风场分布和风速脉动分布, 其中x轴为距激光雷达北-南方向的距离,y轴为距激光雷达东-西方向的距离,z轴为距激光雷达的垂直高度。

图1 算法流程图Fig.1 Flow chart of algorithm

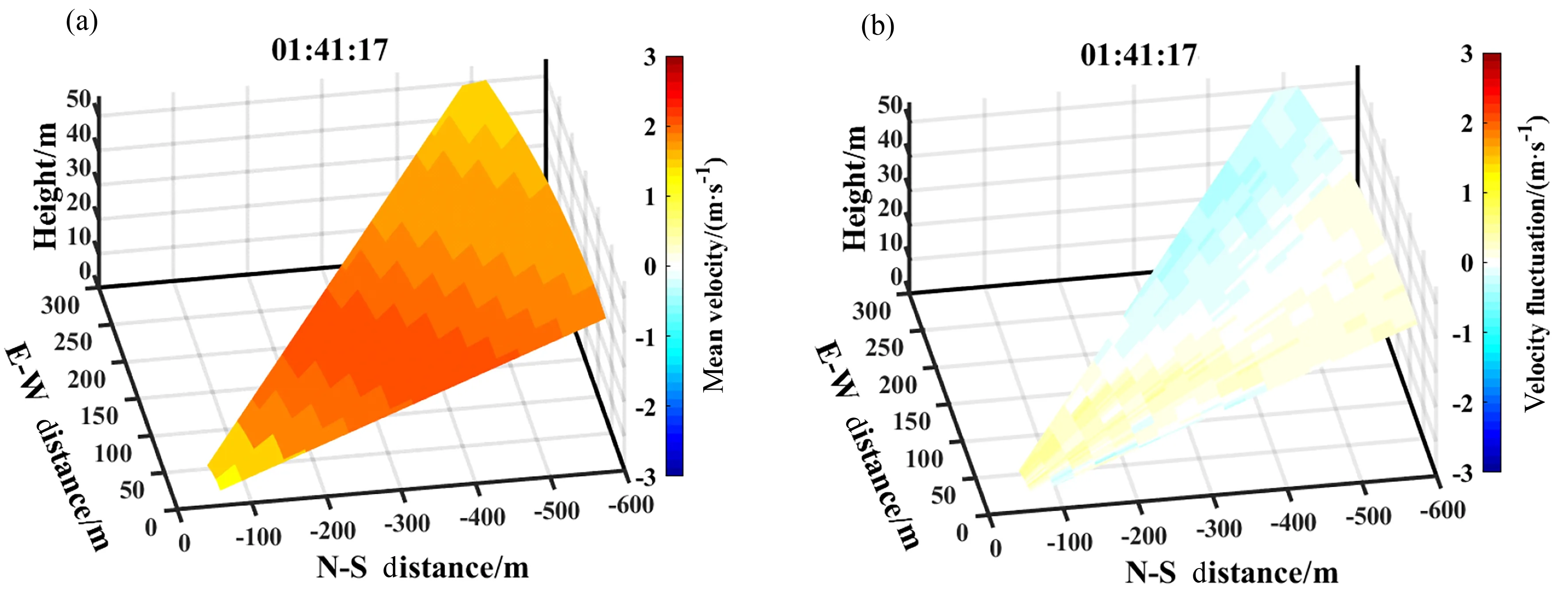
图2 2018年12月15日01:41:17的平均风场分布图 (a) 和风速脉动分布图 (b)Fig.2 Mean radial velocity (a) and radial velocity fluctuation (b) of wind field at 01:41:17 on 15 December 2018

为获取倾斜下滑道区域内的不同空间位置的湍流参数并提高运算效率, 采用空间区域划分方法将扫描区域划分为多个子扇区 (每个子扇区尺度为 5°方位角、2个距离库), 计算每个子扇区内的横向结构函数并使用自协方差法进行系统随机误差校正。后将计算的结构函数与模型结构函数进行最小二乘法拟合, 获得大气湍流参数ε。图3为距离激光雷达210 m处的计算结构函数与修正后的模型结构函数的拟合效果图, 此时对应的横向分辨率为 0.2 m, 远小于拟合出的湍流积分尺度74.28 m, 符合横向结构函数法的适用前提, 反演出的湍流参数数值可信。

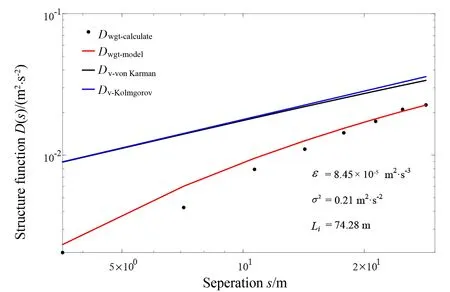
图3 2018年12月15日01:44:28距激光雷达210 m处的结构函数估计Fig.3 Structure function estimation of turbulence at 210 m from the lidar at 01:44:28 on 15 December 2018

2 结果与分析

2.1 实验设置

中国海洋大学于2018年11月至2019年8月在某机场开展湍流观测实验。机场所在区域于秋冬季节盛行西北风, 且风速较大, 跑道端周围多建筑与高大树木, 下垫面情况复杂, 易产生地形诱导风切变。实验期间, 将青岛镭测创芯科技有限公司研制的Wind3D 6000-AP相干测风激光雷达 (详细参数见表1) 安放于机场跑道一端, 安放位置示意图如图4所示。

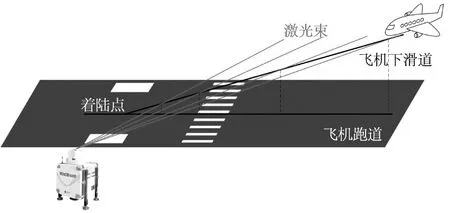
图4 机场下滑道湍流观测模式示意图Fig.4 Schematic diagram for glide path scanning mode of lidar

表1 Wind3D 6000-AP相干测风激光雷达技术指标Table 1 Technical specifications of Wind3D 6000-AP coherent wind lidar

实验中激光雷达的观测模式为下滑道扫描模式。本次实验中激光雷达安放位置距离跑道边缘线约为70 m, 以保证激光光束与下滑道夹角不大于30°, 减小侧风分量的影响, 使激光雷达径向风速可以近似代替飞机真实经历的风速(真实风速在跑道方向上的风速分量)。下滑道扫描模式下的激光雷达扫描参数为: 俯仰角范围3°～4°, 方位角范围148°～174°, 方位角的扫描速度约为0.2 °/s～0.3 °/s, 距离分辨率为30 m, 风速测量精度约0.1 m/s, 风向测量精度约5°。

2.2 数据分析和讨论

2.2.1 稳定大气条件下的观测数据

安放在机场跑道南端的激光雷达于2018年12月15日01:38―01:50获取的径向风速分布如图5所示, 其中x轴为距激光雷达北-南方向的距离,y轴为距激光雷达东-西方向的距离,z轴为距激光雷达的垂直高度。图中颜色表示风速大小, 暖色表示风向远离激光雷达, 冷色表示风向朝向激光雷达。通过图5的序列图可以发现该时段内近地面的风速普遍高于1.5 m/s, 且不存在明显的大气扰动现象, 揭示该段时间内大气状态稳定。

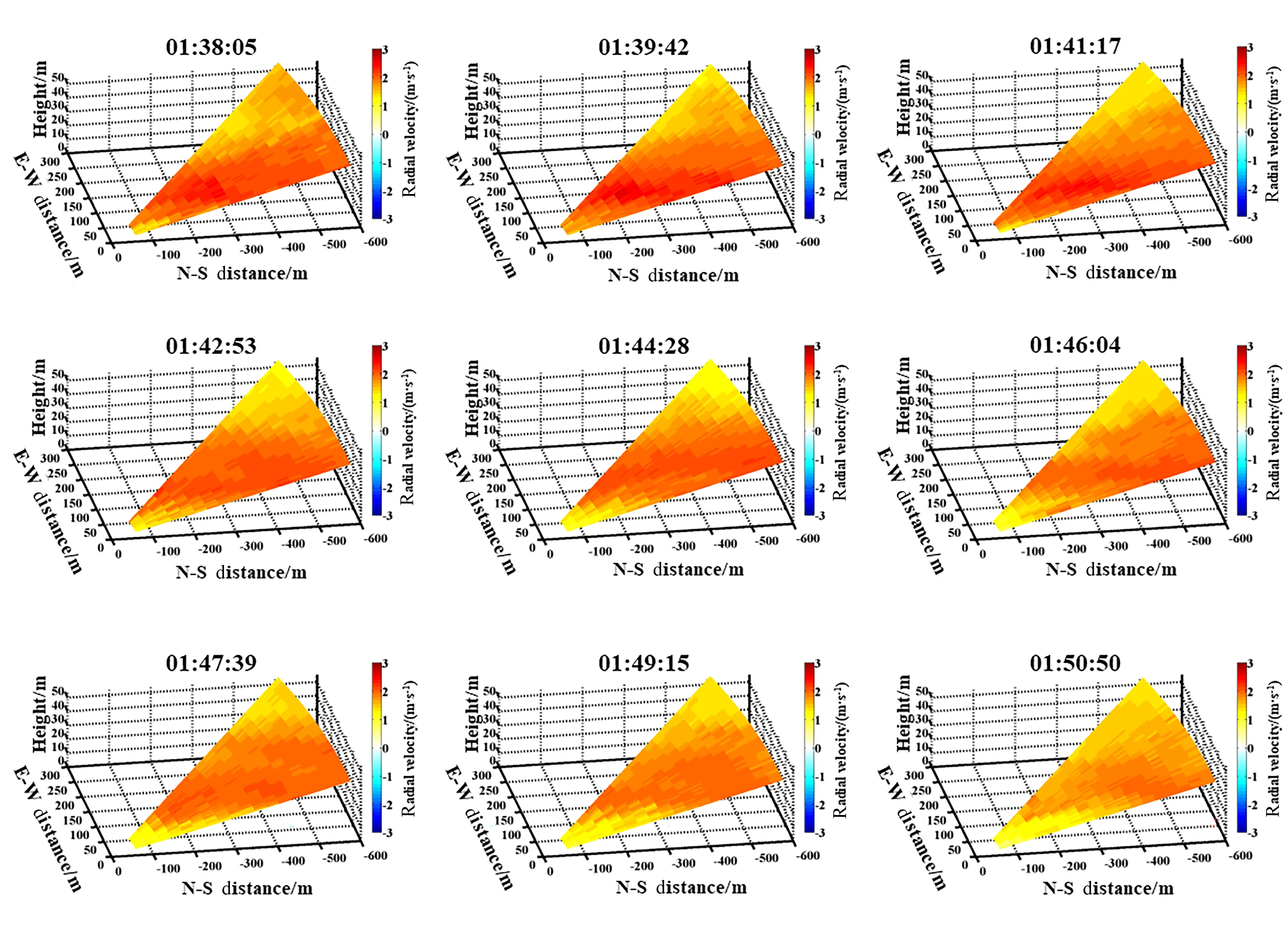
图5 2018年12月15日01:38―01:50径向风速分布图Fig. 5 Distribution of radial wind velocity during 01:38―01:50 on 15 December 2018

将每次扫描反演得到的不同空间位置的大气湍流参数按照空间位置作图, 如图6所示。图中的原点位置为激光雷达的布放位置,x轴为距激光雷达北-南方向的距离,y轴为距激光雷达东-西方向的距离,z轴为距激光雷达的垂直高度。整个下滑道扫描区域被划分为45个子扇区, 每个子扇区的方位角扫描范围为5°、径向距离范围为60 m。每个子扇区反演获得子扇区内空间的平均湍流特征参数, 将每次扫描的148.4°～174°方位角范围、60～600 m径向距离范围区域中的45个子扇区内的ε1/3取均值, 代表一次扫描区域内的平均大气湍流强度状况,ε1/3的平均值和相应的标准差 (——-ε13±σ) 在每个图窗中进行了标注。由图6可知, 2018年12月15 日01:38―01:50 内, 湍流状况较为稳定。ε1/3值主要分布在0.03～0.07 m2/3/s 之间, 每次扫描区域内的空间平均ε1/3为0.047～0.059 m2/3/s。在01:42:53, 激光雷达观测到了发生在其南侧约60～250 m、东侧0～100 m范围内一次相对较强的湍流现象,ε1/3最大值达到0.16 m2/3/s。同样地, 在01:47:39, 激光雷达南侧约60～300 m、东侧0～100 m范围处也出现了一次相对较强的湍流现象, 激光雷达估计的ε1/3最大值达到了0.12 m2/3/s, 属于轻度湍流。

2.2.2 波动大气状态案例分析

2018年12月15日凌晨02:22―02:35, 跑道南端的激光雷达共进行了9次扫描, 反演获取了约13min的径向风速, 如图7所示。该时间段内的ε1/3空间分布图如图8所示, 每次扫描空间内ε1/3的平均值和相应的标准差 (——-ε13±σ)在每个图窗中进行了标注。图7、图8的坐标轴与图5、图6一致。结果显示该时段的近地面径向风速小于1 m/s, 且存在较为明显的大气扰动现象。可以看出, 2018年12月15日02:22―02:35,ε1/3主要分布在0.04～0.08 m2/3/s之间, 每次扫描区域内的ε1/3空间平均值为0.044～0.081 m2/3/s。在02:30:51的观测数据显示下滑道区域内存在非常明显的湍流强度增大现象, 位置大概在激光雷达南侧150～450 m、东侧0～150 m范围内,ε1/3最大值达到0.28 m2/3/s。

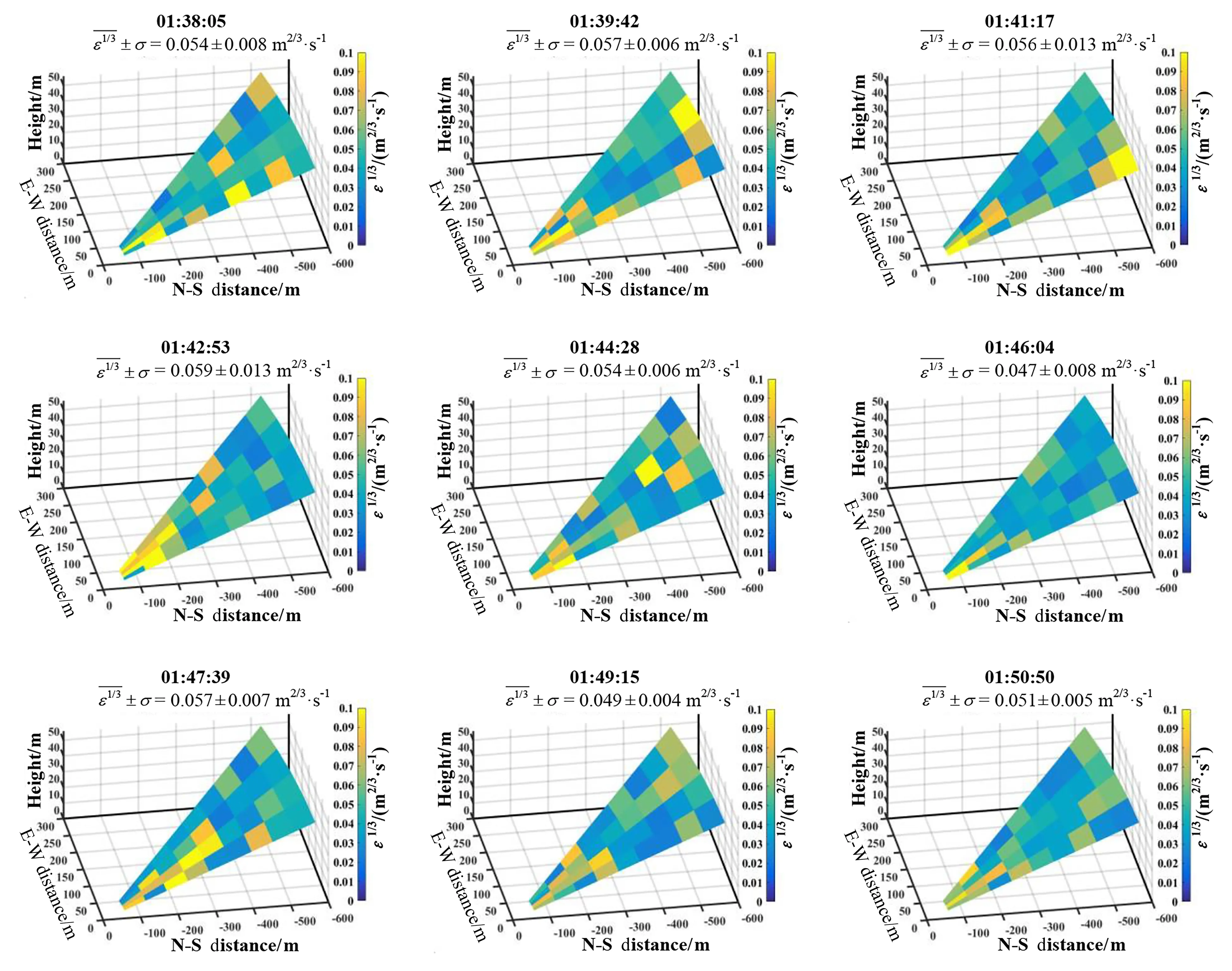
图6 2018年12月15日01:38―01:50 ε1/3 的空间位置分布图Fig.6 Spatiotemporal distributions of ε1/3 during 01:38―01:50 on 15 December 2018

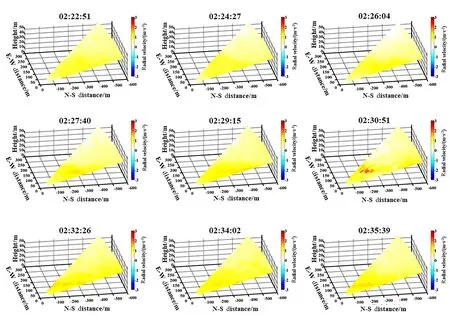
图7 2018年12月15日02:22―02:35径向风速分布图Fig.7 Distribution of the radial wind velocity during 02:22―02:35 on 15 December 2018

2.2.3 湍流特征参数与风切变强度对比印证

为验证湍流特征参数反演算法的准确性, 采用经验证的下滑道风切变识别法[18]计算的风切变强度值进行对比印证。下滑道风切变识别法通过逆风廓线的增大或减小来判断飞机在某一特定方向上是否遭遇风切变。该方法可以进行风切变强度值Iraw的计算, 即

式中 ΔV是一段距离内风速的总变化值;Vapp是飞机的平均进近速度, 一般取 75 m/s; ΔV/R1/3是风速在下滑道上的变化率,R是风切变发生的长度, 即飞行轨迹上风切变的长度。与ε相似, 同样以风切变强度值Iraw的立方根进行强度等级的划分, 当该值在0.3～0.5 m1/3/s2/3范围时, 为中等强度风切变; 当该值大于0.5 m1/3/s2/3时,为严重风切变[19,20]。

对Iraw与ε进行量纲分析, 发现两者量纲相差m/s, 同时, 飞机进近速度Vapp为固定常数, 与观测数据无关。因此, 为更好地对ε1/3对比印证, 将式(11)中的平均进近速度项Vapp去除, 则调整后的风切变强度值I与ε的量纲相同, 即

调整后的风切变强度值I的立方根在进行强度等级划分时, 也需要相应调整为I的立方根。在1.3～2.1 m2/3/s范围时, 为中等风切变强度;大于2.1 m2/3/s时为严重风切变。

图9为2.2.1节和2.2.2节所述两个观测个例中01:42:53与02:30:51的ε1/3空间分布情况与对应时刻的逆风廓线对比。图9 (a)和图9 (c)中, 原点为激光雷达的布放位置,x轴为距激光雷达的距离,y轴为逆风风速值。可以看出两次大气扰动在逆风廓线数据和数据中都有所体现, 并且两种方法获得的结果在时间上较为一致。两次扰动较弱, 均未达到轻度风切变阈值, 在逆风廓线中并无明显体现, 但ε1/3的最大值达到轻度湍流阈值,且在ε1/3的空间分布图中能够被明显观察到。下滑道风切变探测反演方法通过衡量较短时间内风矢量的突变情况判断风切变的发生位置与强度。相较于风切变强度值, 应用下滑道扫描模式的横向速度结构函数法反演得到的湍流参数去除了背景平均风场, 对空间内存在的小尺度湍涡更加敏感。

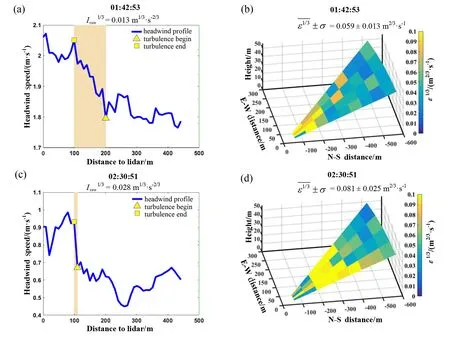
图9 2018年12月15日01:42:53逆风廓线 (a) 与ε1/3空间分布 (b) 以及02:30:51逆风廓线 (c) 与ε1/3 空间分布 (d)Fig.9 Headwind profile (a) and spatiotemporal distributions of ε1/3 (b) at 01:42:53, headwind profile (c) and spatiotemporal distributions of ε1/3 (d) at 02:30:51 on 15 December 2018

图10 (a)和图10 (b)分别为2018年12月15日 01:38―01:50时段内9个扫描片段与02:18―02:38时段内14个扫描片段的I1/3与单次下滑道扫描区域内的空间平均ε1/3对比。在01:38―01:50时段, 激光雷达观测范围内的大气状态稳定,I1/3与空间平均ε1/3均无明显起伏; 在02:18―02:38时段激光雷达观测到一次较为明显的大气波动现象 [02:30―02:34 时段, 如图8 (f)―(h) 所示], 两个强度因子随时间的变化趋势具有较好的一致性,I1/3与空间平均ε1/3数值均达到该时段内的最大值。此次对比基本可以印证本文下滑道扫描模式湍流参数反演结果的可信度。

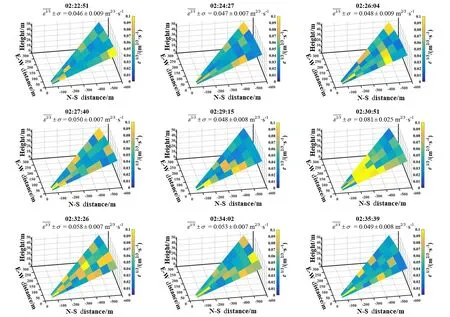
图8 2018年12月15日02:22―02:35 ε1/3 的空间位置分布图Fig.8 Spatiotemporal distributions of ε1/3 during 02:22―02:35 on 15 December 2018

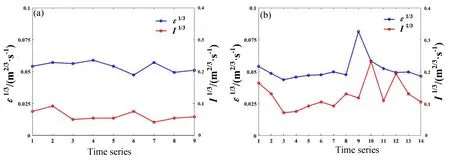
图10 2018年12月15日 01:38―01:50 (a) 和02:18―02:38 (b) 时段的ε1/3 与风切变强度对比Fig.10 Comparison of ε1/3 and I1/3 during 01:38―01:50 (a) and 02:18―02:38 (b) on 15 December 2018

3 结 论

应用高时空分辨率相干多普勒激光雷达观测数据, 采用横向结构函数法估算出凌晨两个时间段 (01:38―01:50、02:22―02:35)下滑道扫描模式的斜程湍流参数, 分析了观测时段内大气湍流参数的斜程空间分布情况, 捕捉到了较为稳定大气状态下的轻微大气扰动。将估算的大气湍流强度与使用相同数据、不同计算方法计算的风切变强度值进行比对, 二者的变化趋势具有较好的一致性。然而风切变强度只代表下滑道方向上的风切变强度水平, 而空间平均后的ε1/3代表一次下滑道扫描范围内的整体湍流强度水平, 因此两者在时间上的变化趋势无法完全对应。

斜程湍流参数的观测反演研究具有广阔的应用前景, 如在气象观测中获取复杂地形条件下的湍流信息,校正天文望远镜在斜程观测中因大气湍流造成的观测误差等。在后期的实验中计划在激光雷达的扫描区域内设置多个安装超声风速计的测风杆, 利用超声风速计的数据对激光雷达反演的湍流参数进行验证对比, 修正大气湍流反演算法, 进一步提高激光雷达的大气湍流探测反演精度。

致谢: 感谢青岛镭测创芯科技有限公司在现场观测实验和数据获取中提供的帮助， 感谢中国海洋大学激光雷达课题组的戴光耀、刘晓英在问题讨论过程中提出的建议。