既有框架结构隔震改造后体系稳定性与动力响应分析
2023-02-13吴巧智马肖彤曹纪兴谭伏波高宁泉
吴巧智, 包 超, 马肖彤, 曹纪兴, 谭伏波, 高宁泉
(1. 宁夏大学土木与水利工程学院, 宁夏 银川 750021; 2. 北方民族大学土木工程学院, 宁夏 银川 750021;3. 同济大学结构防灾减灾工程系, 上海 200092; 4. 宁夏建筑设计研究院有限公司, 宁夏 银川 750021;5. 宁夏建设投资集团有限公司, 宁夏 银川 750021)
0 引言
抗震设防烈度变更、服役性能退化、以及建筑功能改变等因素造成建筑结构抗震性能难以满足新的安全需求[1],既有建筑的加固改造成为解决这一问题的有效途径[2]。其中,隔震技术是40年来地震工程最大革命性创新成果[3],通过阻断地震能量向上部结构的传递,可以有效保护结构安全。
2021年12月颁布实施的《建筑隔震设计标准(GB/T 51408—2021)》,对于隔震结构设计中,上部结构、隔震层以及下部结构做出了详细的技术要求[4],为新建建筑隔震提供了可靠保障。在既有建筑隔震改造工程中,对于由长细比较大的框架柱改造而来的下支柱,普遍基于压杆稳定原理采用增大下支柱截面的方法来提高其受压稳定性。然而问题在于,由于缺少相关规范理论支持,下支柱截面是否需要增大,以及增量大小如何确定均难以准确衡量,加之现行规范未考虑串联体系各部之间的相互作用问题,使其更加难以确定。串联隔震体系动力稳定问题的研究主要由国内学者完成。周锡元等[5]通过对橡胶支座与RC(Reinforced Concrete)柱串联组成的隔震系统建立力学分析模型,给出了体系各部分的水平刚度与临界力计算公式以及整体的水平刚度计算公式。杜永峰等[6]对叠层橡胶支座与地下室柱所组成的串联隔震结构采用数值模拟方式进行竖向单调加载试验,对比底部不同形式的串联隔震体系竖向承载力性能,以及竖向承载力-位移曲线的关键影响因素。刘彦辉等[7]分析了串联隔震体系的P-Δ效应及叠层橡胶隔震支座转动问题,建立考虑各种作用下的串联隔震体系的力学型,推导出频率方程,然后通过数值模拟的方法求解出该体系的频率与振型。秦熙等[8]模拟了首层悬臂柱无拉梁柱顶隔震结构和有拉梁柱顶结构,研究了悬臂柱截面尺寸的改变对这两种结构动力响应的影响,并考虑重力二阶效应对结构的影响。吴应雄等[9]通过隔震结构模型振动台试验,研究了底层为独立柱结构的地震响应,建议工程应用中若底层结构选取独立柱形式时,应加大其刚度。上述文献说明了串联隔震体系中,下部结构应该增大其刚度,但未开展定量分析且取消理论依据。因此,十分有必要针对实际工程中常用的增加下支柱截面尺寸的方法,综合运用理论推导和数值模拟方法研究了截面尺寸变化对串联隔震体系地震作用下稳定性的影响规律。本文通过简化建立由叠层橡胶支座与下支柱串联隔震体系的力学模型,推导出在弯曲变形情况下,下支柱的临界承载力方程,并分析了静力状态下,下支柱稳定性的影响因素,然后通过有限元软件SAP2000对叠层橡胶支座和不同刚度的下支柱建立整体模型,分析了截面尺寸改变对下支柱、隔震支座、串联整体以及上部结构的影响。
1 下支柱临界荷载理论分析
1.1 串联隔震体系理论模型建立
下支柱、叠层橡胶支座以及上部结构组成的串联隔震体系受力变形如图1(a)所示,在地震作用下,上部结构基本只作“整体平动”[10]。由于隔震支座存在剪切刚度和弹性恢复力,所以串联隔震体系中的下支柱不同于理想悬臂柱;与此同时,由于隔震支座的剪切刚度和弹性恢复力远小于下支柱抗侧刚度,与支座串联的下支墩同样不能看作柱顶铰接;因此,该串联隔震体系压杆稳定性理论上是介于一端固定、另一端铰接约束的压杆,以及一端固定、另一端自由的压杆稳定性之间。忽略下支柱的自重影响,考虑压杆轴心受压的理想情况,在临界力Fcr的作用下,压杆的受力如图1(b)所示。
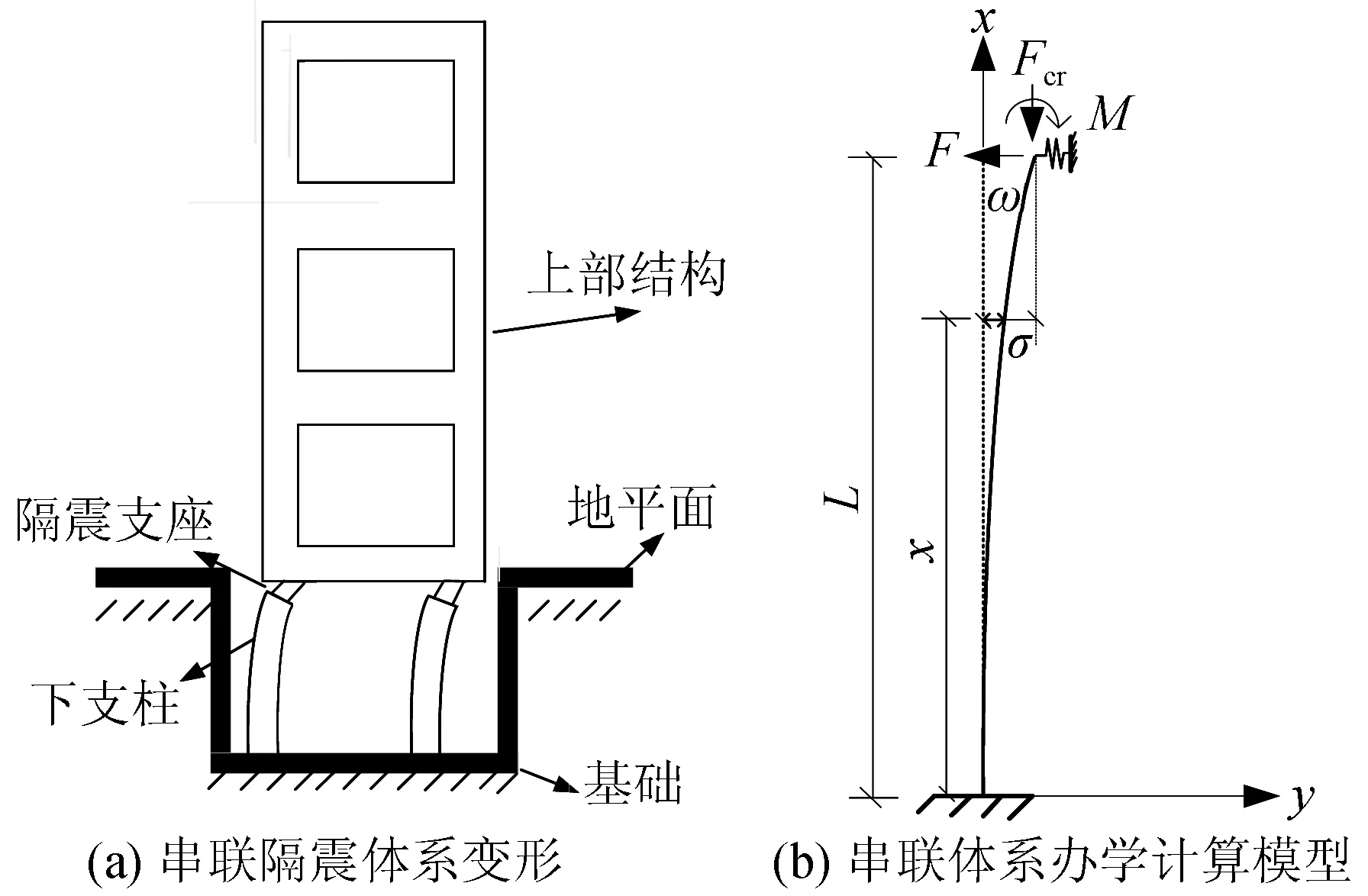
图1 串联隔震体系Fig.1 Series isolation system
1.2 临界荷载求解
根据图1(b)简化后串联体系隔震力学模型,建立坐标系xoy。依据材料力学中用弯剪方程,挠曲线微分方程对该串联体系压杆稳定临界力欧拉公式进行推导。由静力平衡可知,在任意截面处,弯矩之和为0。
M(x)+M+Fcr(σ-ω)-F(l-x)=0
(1)
代入挠曲线近似微分方程可得:
EIω″=Fcr(σ-ω)+M-F(l-x)
(2)
令K2=Fcr/EI,则上式可变为:
ω″+K2ω=K2[σ+(M-F(l-x)/Fcr]
(3)
通过式(3)可解得其通解和其一阶导数分别为:
ω=Asin(Kx)+Bcos(Kx)+σ+
[M-F(l-x)]/Fcr
(4)
ω′=AKcos(Kx)-BKsin(Kx)+F/Fcr
(5)
由下端支承处边界条件知:
x=0,ω=0,ω′=0
代入可解得:
将解的参数A,B代入式(4)和式(5)中,可得到:
(6)
(7)
由下支柱顶点边界条件知:x=l,ω=σ,ω′=θ,代入式(6)和式(7)中可得到:
(8)
(9)
设叠层橡胶支座水平刚度,抗弯刚度分别为K1,K2,则F=σ×K1,M=θ×K2代入式(8)和式(9)中可得到:
(10)
(11)
要从式(10)、式(11)得到F、M的非零解,行列式必须等于零:
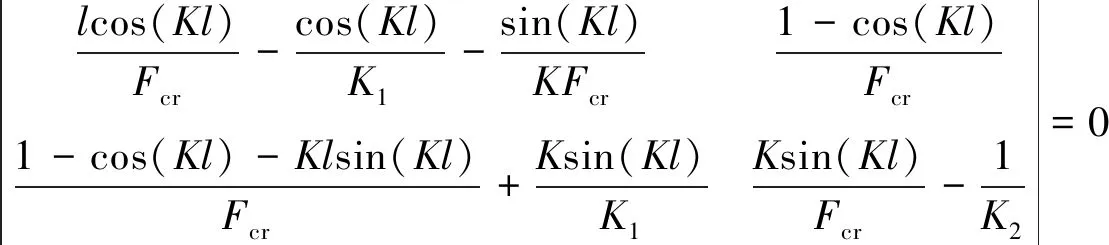
(12)
令:μ=Kl代入式(12)中,化简整理得:
(13)
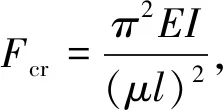
(14)
式中:Fcr为临界压力;F为水平作用力;M为柱顶弯矩;l为下支柱高度;x为下支柱任意高度;ω′、σ和ω为弯曲情况下下支柱任意高度处的转角和挠度;M(x)为任意柱截面处的弯矩;μ为长度系数;E为钢筋混凝土柱的弹性模量;I为下支柱柱截面惯性矩;K1为叠层橡胶支座的水平刚度;K2为叠层橡胶支座的抗弯刚度。公式(14)可以看成为对未知数μ的方程式,依据l、E、K1和K2的具体数值,求得μ的最小非零解,最终可解出临界压力Fcr。
1.3 算例分析
以一根高4.2 m的钢筋混凝土柱进行算例求解,采用C35混凝土,纵筋和箍筋都采用HRB400,下支柱截面尺寸b×h为450 mm×450 mm。对于钢筋混凝土构件,开裂前,采用有效惯性矩法计算截面的弯曲刚度,该方法是将钢筋面积通过弹性模量之比折算成等效的混凝土面积,使折算前后的弯曲刚度相等。构件的弯曲刚度如以下公式[11]所示:
B0=EcI0
(15)
(16)
(17)
(18)
式中:Ec为混凝土的弹性模量;Es为钢筋的弹性模量;I0为换算截面的惯性矩;X0为受压区高度;ρ1为受拉钢筋的配筋率;ρ2为受压钢筋的配筋率;ρ为拉、压钢筋的配筋率之和;As为拉区钢筋面积;A′s为压区钢筋面积;a′s为保护层厚度。叠层橡胶垫的等效弯曲刚度EeI可按以下经验公式[12]计算:
(19)
(20)
当n较大时(如20层以上):
(21)
式中:E0为橡胶的杨氏弹性模量;S1为第一形状系数;tR为胶片厚度;ts为钢板厚度;系数B一般可取为1/2或2/3。代入相关参数的确定值,解得支座的抗弯刚度为3.8×106N·m2。已知其水平刚度为2.6×106N·m2。通过上面公式求解得到钢筋混凝土弯曲刚度和叠层橡胶支座的抗弯刚度,水平刚度,将具体的数值代入式(14)中,该方程为关于μ的超越方程,运用Matlab软件编程求解,解得μ值大约为2.06。假设K1,K2分别为无穷大,则下支柱两端相当于固定约束,解得μ值大约为0.5,从而验证了公式推导的正确性。
通过上式解得临界承载力表达式,改变其中典型的参数,绘制出图2所示的曲线图。从图中可以看出柱高与临界压力呈反比例关系,随着下支柱高度的增大而逐渐降低,当柱高介于3 700 mm到4 200 mm之间,下降率达到了22.39%,之后下降速率逐渐小幅度均匀减小,速度变得平缓;柱截面尺寸与临界承载力成正比关系,当截面尺寸在450 mm×450 mm到500 mm×500 mm时,增长率达到46.93%,之后增长速度变得平缓,几乎呈均匀增长趋势,当截面尺寸在950 mm×950 mm到1 000 mm×1 000 mm的时候,增长率达到22.3%;在下支柱高度和截面尺寸共同作用下,可以得出柱高对临界压力的影响程度要大于柱截面尺寸的影响程度。
2 串联隔震结构模型设计
为了验证理论分析结果,建立隔震设计模型。图3为隔震模型的正立面图和侧立面图。该钢筋混凝土框架上部结构共用有5层,上部结构层高分别为4.2 m、3.9 m、3.6 m、3.6 m、3.6 m,地下室下支柱高度取4.2 m,柱截面宽度和高度取值相同,边长从0.6 m依次变化到1.1 m。纵向4跨,跨度为6 m,横向3跨,跨度为4 m。梁,柱采用C35级别混凝土,钢筋等级为HRB400。该结构按照乙类建筑设计,抗震设防烈度为8度,设计基本地震加速度值为0.20g,设计地震分组为第一组,特征周期为0.35 s,设计使用年限为50年,建筑场地类别为Ⅱ类,框架结构抗震等级为二级,结构安全等级为二级。
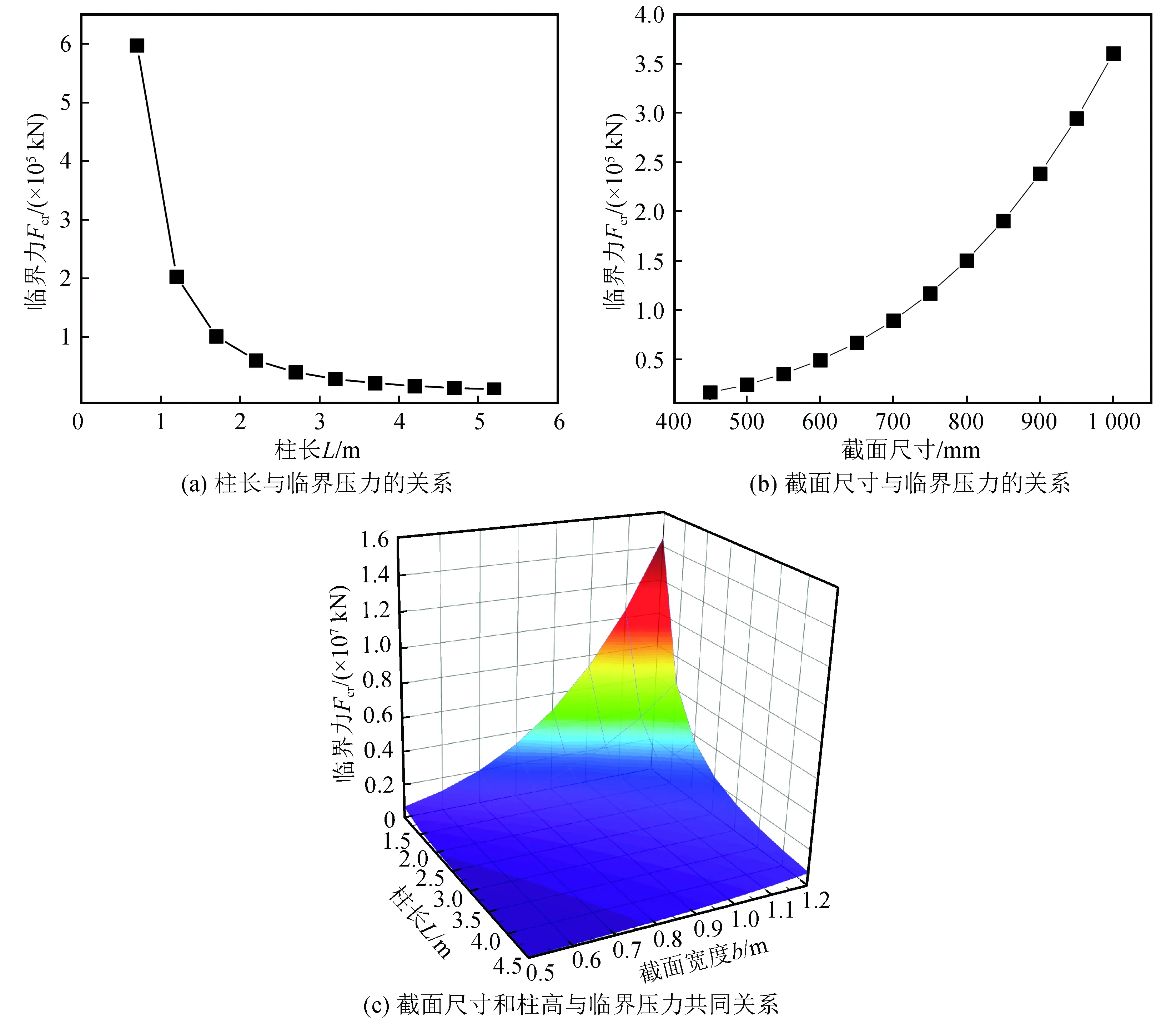
图2 典型参数与临界压力的关系Fig.2 Relationship between typical parameters and critical pressure
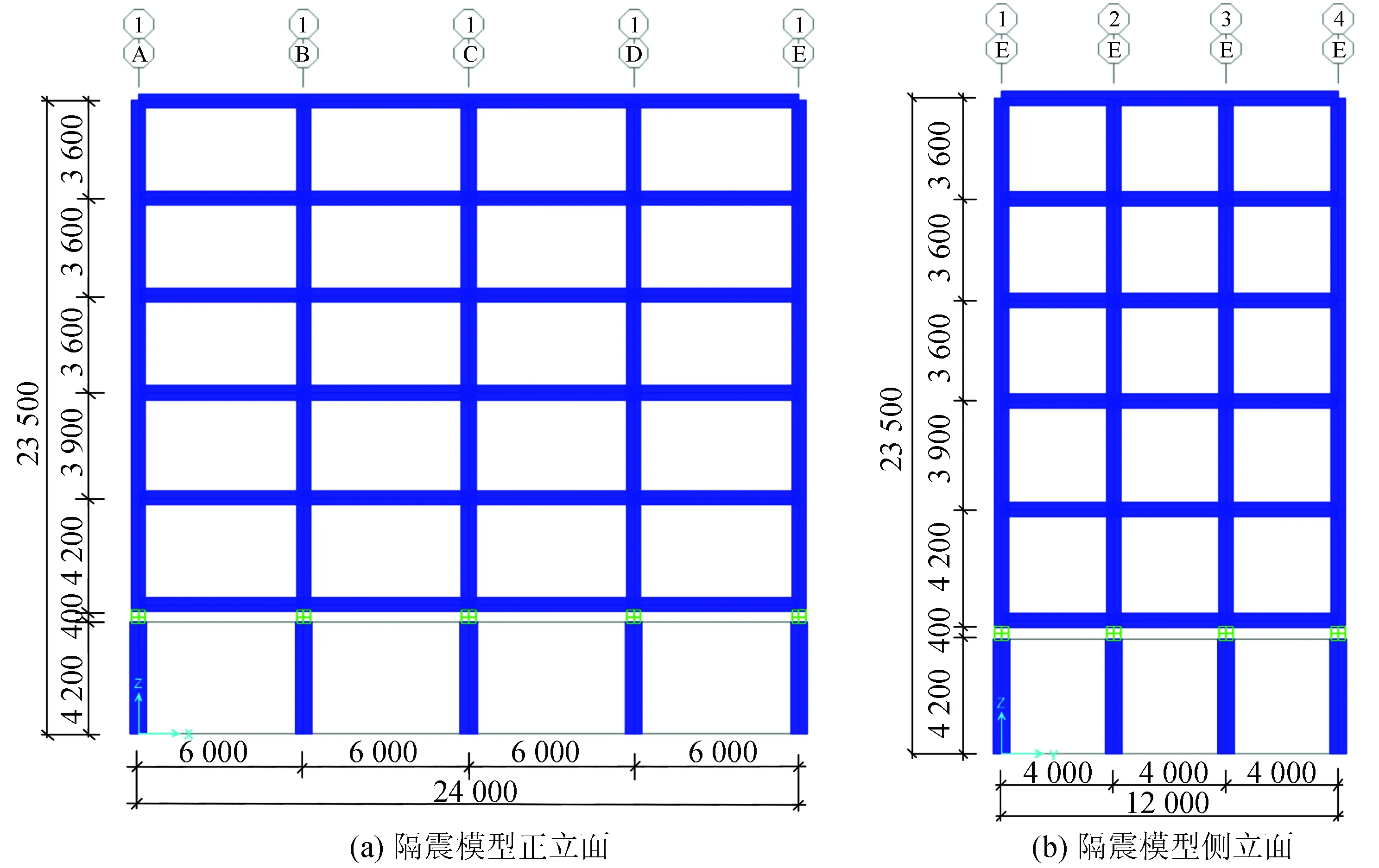
图3 隔震模型图(单位:mm)Fig.3 Isolated model (Unit:mm)
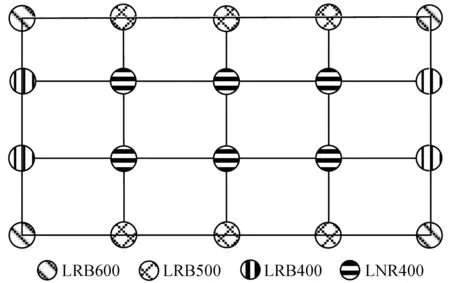
图4 隔震支座布置图Fig.4 Arrangement of isolation bearings

表1 隔震支座参数
针对天然橡胶隔震支座和铅芯橡胶隔震支座的水平变形,各种研究表明:地震装置的本构定律对静态或动态载荷条件敏感,所以严格遵守了《建筑抗震设计规范(GB 50011—2010)》[13],确保隔震装置的本构定律合理。在静态条件下,即隔震装置的剪切应变等于0,使用屈服前的刚度;在动态条件下,即隔震装置的剪切应变等于100%和250%,分别对应于设防地震和罕遇地震,将水平等效刚度,等效阻尼比和屈服后刚度应用于材料模型。
3 地震反应分析
3.1 下支柱柱顶水平位移响应
本文选取了三条实际强震记录地震波,El-Centro波(南北分量)和Taft波(南北分量)以及Kobe波(南北分量),分别调幅至设防地震加速度0.2g和罕遇地震加速度0.4g。
图5(a)所示为设防地震下6种计算模型中下支柱顶部位移。可以看出,随着柱截面的增大,柱顶位移呈现递减趋势,侧面反映出下支柱的极限承载力逐渐增大,这一规律与所推导的临界力压杆稳定公式变化规律相一致。柱截面增大,下支柱抗侧刚度增强,抗震性能得到提升。截面宽度从600 mm增大到1 000 mm时,每增加100 mm,可以得出在每一条地震波作用下,柱顶位移在数值上几乎以48%的递减率减小;截面宽度由1 000 mm增大到1 100 mm时,位移减小量均值为0.27 mm,柱顶位移变化量极小,下支柱位移趋于恒定。
针对串联隔震体系而言,最不利的工作状态就是在罕遇地震水准的水平地震作用下,隔震支座和下支柱发生了较大的水平位移,并承受着设计竖向荷载的情况。图5(b)为在罕遇地震下,下支柱柱顶位移响应。在罕遇地震下,柱顶位移值约为设防地震下位移值的2倍,下支柱截面尺寸逐渐增加,柱顶位移规律大致与设防地震下规律相符合。柱截面尺寸为1 000 mm×1 000 mm时,在Taft波和Kobe波下柱顶位移响应几乎一致,数量值上相差0.13 mm,柱截面增大对下支柱的抗侧刚度影响不太明显,从图2也可以得出其临界荷载值趋于定值。柱截面尺寸继续增加,只会影响建筑物下部空间的使用功能,提高其经济成本,对于地下室柱的抗震性能所起作用极小。
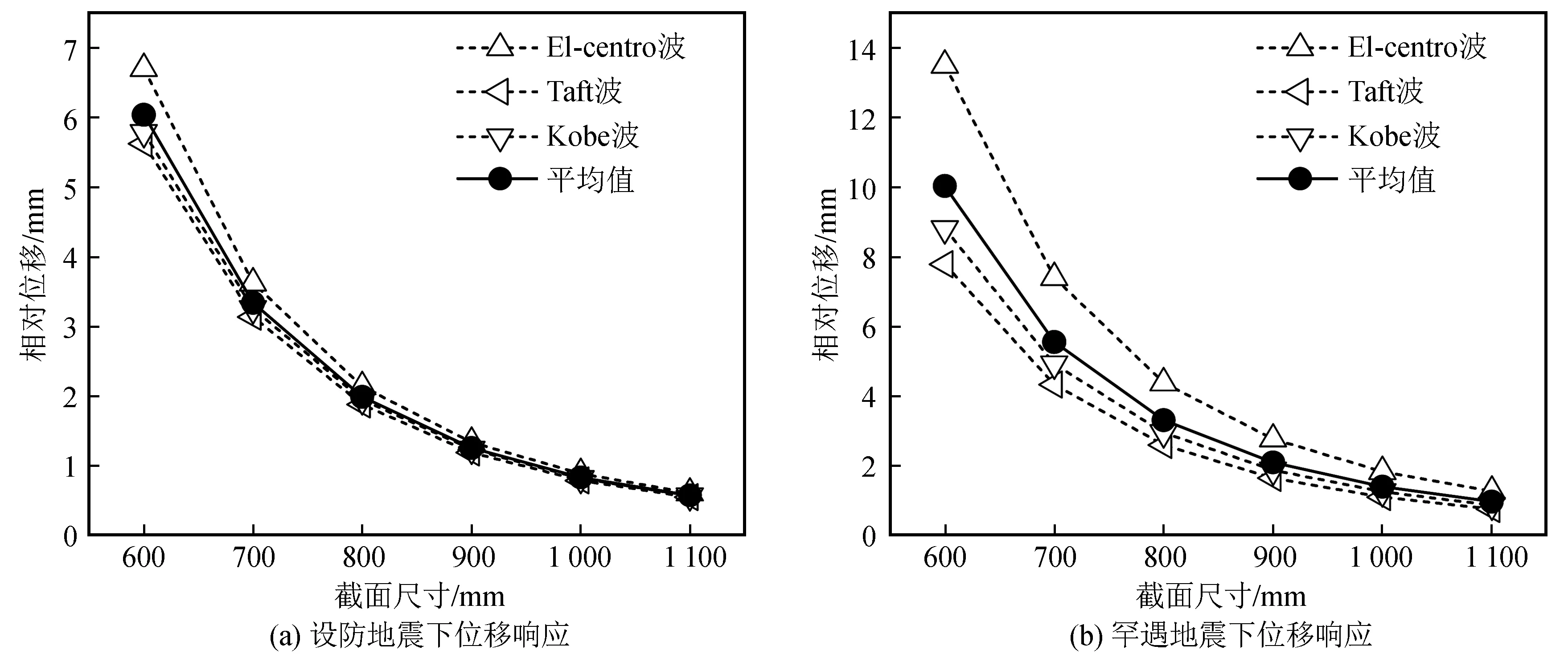
图5 地震作用下下支柱柱顶的响应Fig.5 Response of lower pillar top under earthquake action
3.2 隔震支座和串联整体水平位移响应
隔震支座的水平位移限值不应超过其有效直径的0.55倍和各橡胶层总厚度3倍二者的较小值[14],即1/θ≤min(0.55D,3Tr),该模型中隔震支座最大位移值均小于规定限值。从图6中可以看出,无论是在设防地震还是罕遇地震下,下支柱截面的变化与隔震支座位移成正相关关系,但是增长速率特别小,基本保持在4.72%以内。
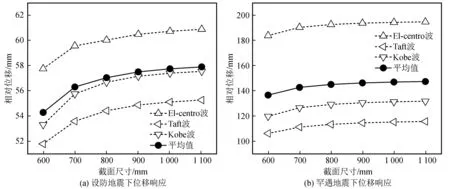
图6 地震作用下隔震支座的响应Fig.6 Response of isolation bearings under earthquake action
为了研究下支柱与隔震支座串联后整体的相互作用效果,现对隔震层楼板处位移进行分析。该水平相对位移值为下支柱和隔震支座相对位移值之和,叠加后的位移值与下支柱端部的位移相比显著增加,因为隔震支座是一种软连接装置,该装置在地震作用下变形比较大,但可以将地震80%左右的能量抵消掉。由图7知,下支柱截面增加,整体的位移逐渐减小,在设防地震下,当柱截面增大到900 mm时,位移递减率在1.5%左右,截面继续增大,递减率保持在0.3%以内,位移值几乎保持恒定。罕遇地震对框架结构的激励效果显著,在三条自然地震波作用下,柱截面为600 mm×600 mm时,整体的最大位移平均值达到了154.51 mm。同理,每一条地震波下,位移值随着柱截面尺寸增大逐渐减小,变化趋势平缓,当下支柱截面达到1 000 mm时,位移值几乎不再变化。
3.3 上部结构层间位移角响应
各楼层和地下室层的地震响应用层间位移角来表示,层间位移角是对构件截面大小,刚度大小的一个宏观控制指标,目的主要为限制结构在正常使用条件下的水平位移,确保高层结构应具备的刚度,避免产生过大的位移而影响结构的承载力、稳定性和使用要求。每一层的层间位移角取值为3条地震波作用下的平均值,结构在地震作用下,结构楼层内最大的弹性层间位移角应符合《建筑隔震设计标准(GB/T 51408—2021)》中相关规定[4]。从图8可以得出,上部结构在设防地震和罕遇地震下,层间位移角小于其限值1/400、1/100,下部结构层间位移角同样小于其限值1/500、1/100,地下室层层间位移角随着下支柱截面尺寸的增大而逐渐减小。当尺寸在600 mm×600 mm到700 mm×700 mm时,下降率达到44.3%左右,之后下降率逐渐降低,速度变得缓慢;柱截面尺寸为1 000 mm×1 000 mm时,截面继续增大,层间位移角相差特别小,几乎不再变化;随着截面尺寸的增加,上部结构的层间位移角略有增加,增长速率基本保持在7.6%以内。
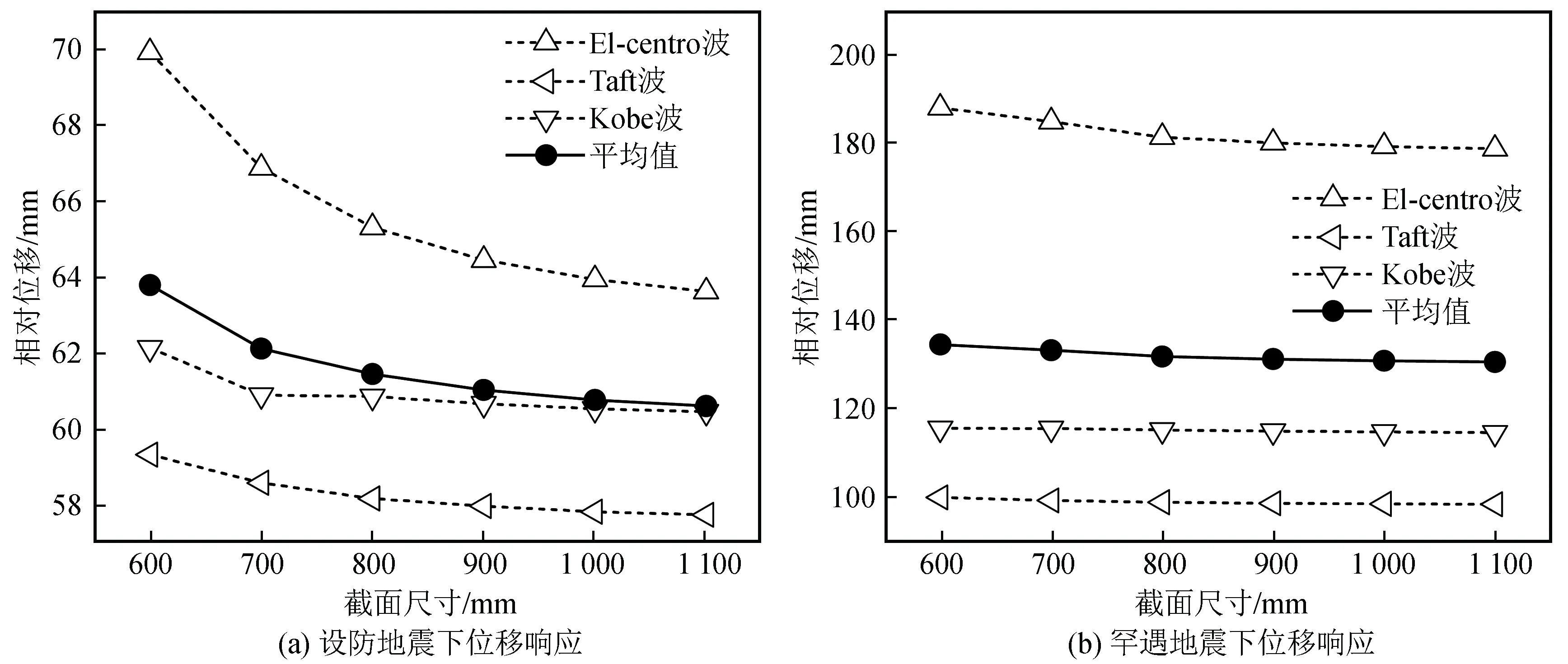
图7 地震作用下串联整体的响应Fig.7 Response of series isolation system under earthquake action
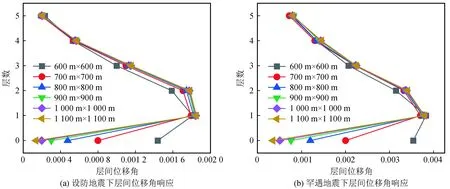
图8 地震作用下上部结构和下支柱的响应Fig.8 Responses of superstructure and lower pillar under earthquake action
4 结论
针对隔震改造后叠层橡胶支座和地下室框架柱组成的串联隔震体系地震稳定性问题,系统研究了所推导出的体系临界承载力变化规律与影响因素,以及整体结构地震响应特征,得到如下结论:
(1) 对于改造而来的地下室柱顶隔震结构,需重点关注罕遇地震作用下的下支柱地震响应。条件允许时应适当增强下支柱抗侧刚度,从而提高其受压稳定性。
(2) 当下支柱柱截面尺寸增加时,其柱顶和串联整体的位移响应逐渐减缓,隔震支座的位移响应和上部结构层间位移角响应略有增加。
(3) 在既有建筑隔震改造时,建议先进行整体结构在数值模拟下的地震响应验算,在同时兼顾下部建筑空间的使用需求和下支柱的稳定性的条件下,确定最优的柱截面尺寸。
