台风天气下电网薄弱线路辨识与停电事故模型

于 群，林婧璇，马艳子

（山东科技大学电气与自动化工程学院，青岛 266590）

长期以来，我国福建、广东等沿海地区经常遭受台风灾害的侵扰。在台风环境下，由于输电线路大部分暴露于外部环境，使运行过程中的电力系统不稳定性急剧提升。近年来的“莫兰蒂”、“尼伯特”、“玛莉亚”等台风均给电力企业造成了重大的经济损失，严重影响受灾地区人民的正常用电生活[1-2]。因此，如何快速精准的辨识电网的薄弱环节，构建故障连锁传播模型成为在维持台风天气下电网可靠运行的关键。

目前，对于在台风天气等极端灾害下电力系统的安全评估已有一定的进展。文献[3]从杆塔结构及主材出发，通过ANSYS软件对杆塔结构进行建模，研究杆塔在台风作用下的风载荷效应，得到杆塔受损程度；文献[4]利用Batts模型刻画台风衰减过程中风场各点的风速，根据台风与电杆相互作用机理建立杆塔及线路故障率模型，考虑线路故障率与负荷重要程度建立配电网架空线路薄弱环节辨识方法；文献[5]基于经典Rankine模型，结合流体力学软件计算风荷载，从而计算配电线路故障率；文献[6]建立基于极值Ⅰ型概率分布、蒙特卡洛法及随机森林法的输电线路损毁概率预测混合模型，综合考虑气象、微地形、杆塔运行等因素，可提前23 h对薄弱环节进行预警。上述文献使用的风场模型形式相对简单，虽然易于求解但误差较大；且多数研究均着重于杆塔或线路本身的故障率，在评估薄弱环节时未考虑线路拓扑结构与事故规模的关系，从而上升到对大面积区域内停电事故的传播进行研究。在现有研究中，对台风天气等极端灾害下电力系统的连锁故障的研究较少，文献[7]将台风的影响考虑在多时间尺度的连锁故障建模中，研究台风在连锁故障演化过程中的影响，并对事故链风险值进行分析计算，但使用的风场模型较为落后，且在故障分析中未从电力系统整体的稳定程度进行评估；文献[8]则从提升台风天气下配电系统韧性的角度出发，以最小化停电损失、投资成本为目标，建立3阶段鲁棒优化模型。

考虑现有研究存在的不足，本文首先采用Yan Meng风场模型从径向和切向对台风进行刻画，分析台风与线路故障率的关系，建立计及台风强度和路径的线路停运概率模型；然后，对传统的电力系统自组织临界性模型SOC（self-organized criticalitypower failure）进行改进，研究在台风环境下电力系统的自组织临界性，实现从整体的角度对电力系统的稳定度进行评估；其次，考虑台风影响所占比重应随台风运动而变化，结合线路电气介数，制定可随时间和台风强度变化的配电线路脆弱度指标；最后，以玛莉亚台风和宁德（以下简称ND）电网为例，验证了所建立的判断线路脆弱度模型的可行性，并得出台风天气电力系统更易进入自组织临界态的结论。

1 杆塔故障概率

1.1 台风模型

台风对输电杆塔的影响随着时间和空间的变化而变化。台风与电网的位置关系如图1所示。

图1 台风与电网的位置示意Fig.1 Schematic of location of typhoon and power grid

图1中，t1～t3为台风从海域靠近陆地并登陆的过程，台风最大风圈半径所覆盖的陆地面积依次增大，表明台风对电力系统的破坏力与破坏范围依次上升，可能造成的电网停电规模也随之变大。因此，精确的风速预测对分析台风天气电网的运行状态尤为重要。

Yan Meng模型[9]是一种考虑边界层摩擦力修正与地形地貌的压力梯度平衡方程。作为一种经验与数值相结合的模型，引入“等效粗糙高度”，利用某一高度处的风速等于梯度风速与该处摩擦风速之和的原理，来反映台风风场基本特征，并得到较为准确的模拟风速。与经典的Batts风场模型[10]相比，Yan Meng模型考虑了摩擦力，从垂直和水平方向对风场进行求解，更符合实际工程应用。

Yan Meng风场采用Holland气压模型[11]，其中的重要参数为最大风速半径，即台风中心到最大风速位置之间的距离，用Rm表示。Rm与中心气压差的相关系数为负，常用的拟合公式为文献[12-15]提出的4种公式。

考虑边界层摩擦力修正，忽略不计边界层内变化很小的径向气压梯度及边界层上的摩擦力，压力梯度平衡方程可表示为

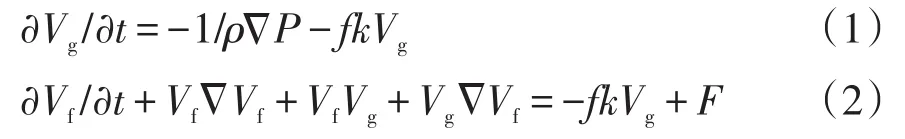
式中：Vg为自由边界层内的梯度风速；Vf为受地表摩擦力影响的风速；t为时间；ρ为空气密度；P为台风气压梯度；f为科氏力参数；k为拟合系数；F为边界层摩擦力。

Yan Meng风场对式（1）和式（2）进行求解，最终风速为Vg和Vf的矢量和。

同一经纬度下风速大小会随海拔高度的不同发生变化，而由上述Yan Meng风场计算的风速为海拔10 m处的风速大小，因此还要对风速进行高度换算。对不同高度的风速Vx进行换算[16]，可表示为

式中：V10为海拔10 m处的风速；Zx为待求风速的海拔高度；Z10为海拔10 m处；a为等效粗糙度，该值随预测地点的地理环境而变化。

1.2 故障概率拟合

每条架空线路是由线路中的各个输电杆塔串联而成，根据历史数据统计，结构参数不同的220 kV与500 kV输电杆塔的抗风能力相似，因此台风风速大小与输电杆塔的失效率可以用同样的指数函数来拟合[17]，即

式中：λi为杆塔的失效率；Vmin为杆塔的设计风速；Vex为极限风速（常取Vex为2Vmin）；K为模型系数。

采用logistic回归[18-19]对失效率进行建模，可进一步得到输电杆塔的故障概率为

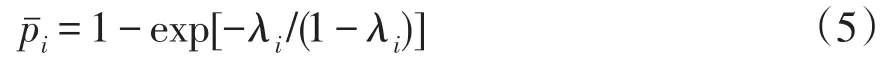
对于一条含有n个输电杆塔的线路，线路中任意位置杆塔的失效都将导致整条线路的停运，因此故障概率为

为综合考虑线路潮流分布与线路故障率，选取故障率高的线路组成初始故障集，当电网中发生初始故障后，其余线路采用基于线路潮流的线路停运概率模型[20]，将计算出的在台风环境下的线路故障率作为初始停运概率，结合每条线的潮流极限值，得出事故后每条线路的停运概率，线路故障与停运概率关系如图2所示。

图2 线路故障率与停运概率关系Fig.2 Relationship between line failure rate and outage probability

1.3 线路脆弱度指标

线路脆弱度是电力系统运行中的重要指标之一。通过建立合理的线路脆弱度评估体系，有利于判断任意时刻电网中相对薄弱的环节，对维护电网的稳定运行具有重要作用。不同线路失效对电网稳定运行的影响力不同，且台风天气对电网的影响是一个随着台风移动而不断变化的过程，因此评估脆弱度指标的因素不应定性和定量。

在由连锁反应导致的大停电事故中，故障的产生和扩散与电网本身的拓扑结构关系密切。在台风影响下产生初始故障后，线路的停运概率与潮流分布密切相关，因此在对线路脆弱度进行评估时，还需将电网拓扑结构带入评估指标。电气介数[21]将电气距离与容量分布相结合，可以很好的反应在各发电机与各负荷节点对之间，输电线路对潮流传播规律的影响。基于线性电路的叠加定理，依次将单位有功功率注入各发电机与各负荷节点对之间，其他节点注入有功功率为0来计算线路潮流。线路电气介数Be(m,n)可表示为

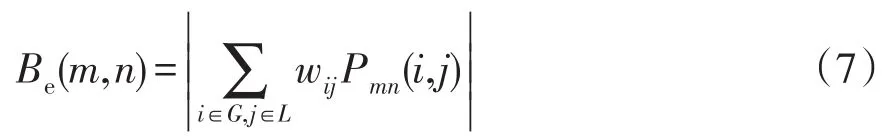
式中：wij为发电机i与节点j间传输的有功功率上限值，wij=min(Si,Sj)，Si、Sj分别为发电机i与负荷节点j注入的有功功率；Pmn(i,j)为从m传输到n的有功功率。

由式（7）计算得出的电气介数值越大，表示线路故障造成的潮流重新分布对电网稳定运行的影响越大，为方便研究可将电气介数进行归一化。

由于电气介数反应的是电网结构对运行稳定性带来的影响，因此各线路的电气介数的数值在时间上保持不变，但其参与到脆弱度指标中的比重会随着台风的移动而变化。将在台风天气下的线路故障率与电气介数进行加权，随着台风位置和风速的变化二者取值也将变化。

2 系统整体建模

2.1 连锁故障模型

台风天气下输电线路的失效往往伴随着连锁故障反应，造成大规模停电事故。目前我国已有学者[22-23]将经典的SOC大停电模型应用于实际电网分析大停电事故，验证了模型的可行性，并得出了我国电网停电事故存在自组织临界性这一重要特征。

SOC模型将电网视作沙堆，将负荷的增长视作沙堆上不断坠落的沙粒，当落下的沙粒达到一定数量，即线路潮流到达极限值时，此时微小的扰动就会引起沙堆的结构失衡，发生大小不一的坍塌，等效为电网发生连锁故障引起的大小不一的停电事故，并在仿真时统计负荷损失量，用损失负荷和发生频率做幂律曲线对自组织临界性进行表征，其幂律关系可表示为

式中：N(Q)为发生规模为Q的事故频率；a为常数；b为分维。

2.2 台风天气下的大停电模型

在台风天气下线路的失效具有随机性与时变性，这同不确定性分析具有相同的特性，因此可以采用非序贯蒙特卡洛模拟法对台风影响进行抽样。将台风天气对线路的影响视作系统的随机大扰动变量，以0，5 h为时间间隔，按故障概率抽取初始故障线路进行事故的演化模拟。在台风影响下电力系统连锁反应故障仿真模型流程如图3所示。

图3 台风影响下电力系统连锁故障仿真模型流程Fig.3 Flow chart of simulation model of power system’s chain-reaction failures under typhoon influence

3 算例分析

3.1 风速预测

本文以中央气象网提供的玛莉亚台风为例。2018年7月9日8：00，玛莉亚台风到达我国台湾东北方向并穿越台湾海峡，7月11日上午经过福建省霞浦东南海域。针对此次台风中灾情较为严重的ND地区，对线路安全进行评估，并对该地在台风经过时的电网线路停电事故进行仿真。

将文献[12-15]提出的4种半径公式分别用于仿真，计算结果可得文献[12]的公式仿真结果最接近于观测值，因此本文使用文献[12]的公式进行计算。

将台风登陆前后每小时的最大风速与中心气压差进行对数拟合，求解得到Holland气压场模型的回归系数，进而得到气压参数B，本例中所得回归系数为0.451 9，B的取值范围为0.438～1.152。由文献[24]可知，在最大风圈以内B的取值对风速影响不明显；在最大风圈以外，B越大风速下降的幅度越大，通过多次计算并与观测值进行对比，在B取0.85时标准差最小。

以玛莉亚台风期间福建省北壁地区气象站数据为观测风速，将Yan Meng模型与经典风场Batts模型进行对比，如图4所示。由图4可以看出，Yan Meng模型的准确度较Batts模型有了明显的提升，证明考虑边界层摩擦力修正与地形地貌的风场模型更符合实际，具有一定的工程应用价值。

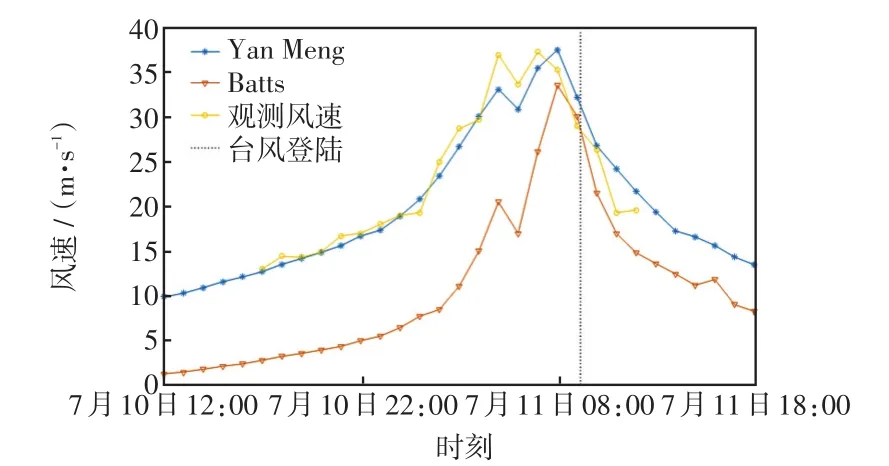
图4 风场模型对比Fig.4 Comparison between wind field models

3.2 脆弱度评估

ND电网是福建省的一个地区电网，地处福建东部沿海，该地多山丘，海拔较高。该电网共67节点、103线、5个发电站，在玛莉亚台风侵袭期间电网的稳定运行遭到极大破坏。

以ND电网为例，通过所提模型分别对正常天气条件和台风天气下的电网进行仿真。其中，台风天气下从7月11日04：00—12：30时段内的台风影响进行仿真，以0.5 h为时间断面，共18个时间点，计算该时段内每个时间断面脆弱度最高线路，其统计结果如表1所示。

表1 7月11日部分时段脆弱度最高线路Tab.1 Lines with the highest vulnerability index in some periods on July 11

由表1可知，以台风过境期间线路脆弱度最高的SJ-YD线为例，取杆塔的设计风速为30 m/s，得到风速大小与输电杆塔的失效率关系，SJ-YD线在7月11日8：30—9：00时段故障率达到峰值；计算各线路电气介数，可得SJ-YD线的电气介数为0.438 7。设线路故障率的阈值为30%，当故障率小于该阈值时，由系统拓扑结构主导事故的演化范围；在台风的移动轨迹逐渐靠近目标地区的过程中，由于风速与故障率呈正相关关系，线路故障率随风速增大而上升，当故障率超过阈值时，事故由台风主导。由此求得的SJ-YD线在台风天气下的线路故障率和脆弱度如图5所示。

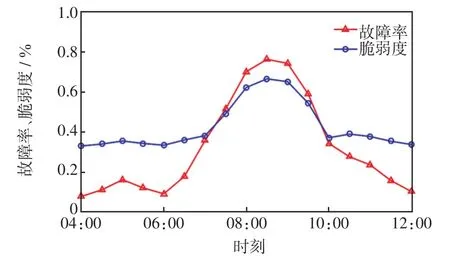
图5 线路故障率与脆弱度Fig.5 Line failure rate and vulnerability index

由于台风受地表摩擦力的影响，风速将呈下降的趋势，因此在最大风速风圈靠近陆地前后，台风对ND电网的影响最为严重，在9：00时刻电网与台风轨迹关系的示意如图6所示。图6中，用加粗标星线段标注SJ-YD线，加粗圆圈为此时的最大风速风圈，此时ND电网开始进入最大风速风圈的范围内，因此8：30—9：00前后为事故的高发时段。

图6 最大风速风圈与电网位置示意Fig.6 Schematic of location of maximum wind circle and power grid

根据实际灾情，ND地区在玛莉亚台风侵袭期间，当地陆续出现停电事故的时段为7月11日上午8：10—9：25分。而计算的最大风速风圈正是在该时段覆盖ND地区，表明在这一时段台风对该地影响范围广、作用力大；此时计算的SJ-YD线故障率大于50%，脆弱度指标大于0.5，与实际受灾情况吻合，证明所提方法计算结果具有一定的准确性，可以作为台风期间对薄弱线路辨识的参考。

3.3 连锁故障模拟

以7月11日8：30时刻为例，计算各线路故障率及脆弱度并分别按大小排序，筛选出排名前五的线路；分别将其设为初始故障线路用于所提模型进行连锁故障仿真并统计其损失负荷，由于本次研究属于不确定性分析，使用蒙特卡洛法抽取故障线路得到的损失负荷有一定的波动，故循环仿真10 000次取损失负荷的平均值以减小误差干扰。计算结果如表2所示。

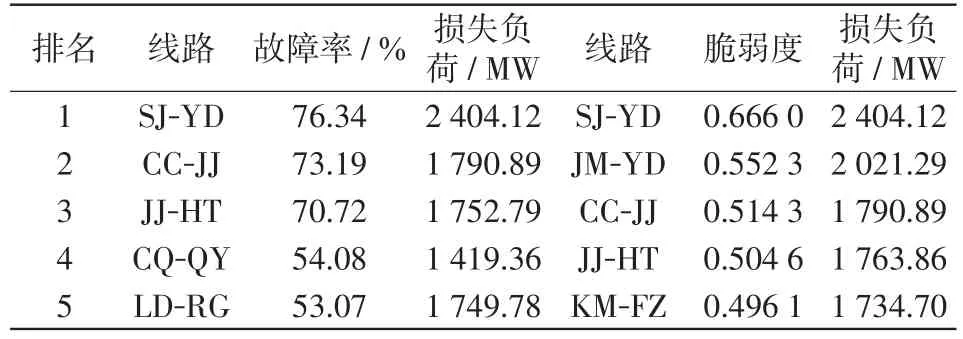
表2 7月11日8:30线路故障率与脆弱度排序Tab.2 Line failure rate and vulnerability index ranking at 8:30 on July 11

由表2可知，在该时刻脆弱度排名前5名的线路中，JM-YD线的线路故障率虽然仅为30.44%，但其电气介数相对较大，表示该线路在电网稳定运行中扮演的“角色”比其他线路重要，其平均损失负荷远大于其他故障率靠前的线路。一旦线路停运JMYD线造成的损失相对更严重；相反，CQ-QY线停运后的平均损失负荷明显小于其他线路，因此虽然其故障率较高，但在评价脆弱度时数值并不靠前。综上，本文所提的脆弱度评价方法不仅考虑台风环境下线路的故障率，还综合考虑了线路与电网整体的联系；不局限于强台风环境下使用，只需在计算脆弱度时改变线路故障率的阈值大小，即可根据环境因素改变各影响因素所占的比重，因此在台风的前期和后期，以及正常天气条件下均可适用，对于实际工程应用更具有参考价值。

使用所建模型对7月11日04：00—12：30时段内的停电事故进行仿真，并用最小二乘法在双对数坐标系中作出事故幂律曲线，横坐标为事故规模的标度，纵坐标为对应事故规模发生的频度，其结果如图7所示。

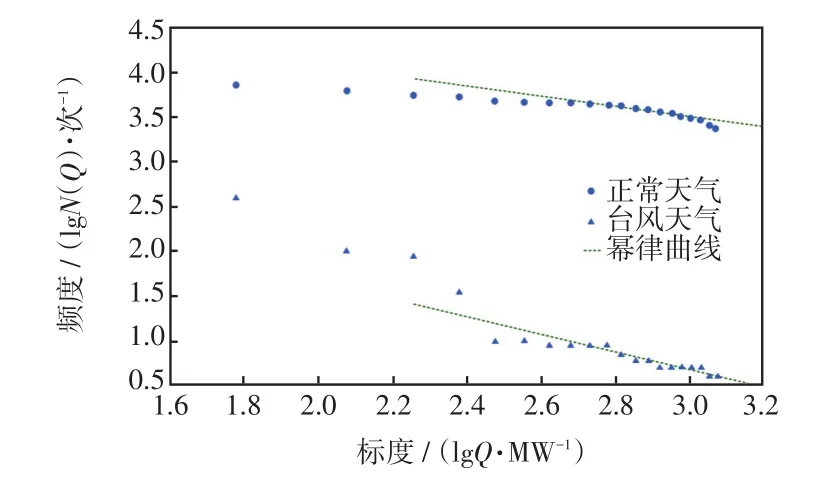
图7 两种天气状态下停电事故幂律曲线对比Fig.7 Comparison of power law curves for power outage accidents under two weather conditions

表3 2种天气状态下停电事故回归方程Tab.3 Regression equation of power outage accident under two weather conditions

根据数理统计理论，对于显著水平α=0.01、n-2=18，查找相关系数显著性检验表，所求得的相关系数均大于R0.01=0.561，表明所求的回归方程有效。由图7结果证明了ND电网无论是在正常天气条件还是台风天气条件下均具有自组织临界性，即电网存在临界状态，当微小的扰动出现时可能引起多条线路过负载退出运行，从而导致大面积停电事故的发生。对比图7中2个幂律曲线，在台风天气下的事故频率整体较正常天气有了明显的提升，自组织临界态也发生了明显变化。分维越大表明系统越不容易进入自组织临界态，抗干扰能力更高，系统稳定性更强，因此，可用分维对电力系统整体稳定性进行评估。本例台风天气时回归方程的分维为0.411 1，明显小于正常天气时的0.983 9，说明在本次台风过境期间，7月11日8：30时对当地电网稳定性带来的影响较大，危及当地正常供电需求，调度人员需提前制定应对方案，尽量缩小事故传播范围，减少停电造成的不便和损失。

4 结语

本文主要研究在台风天气下，电网中各处风速大小的变化与线路故障率之间的关系，并将实时的线路故障率与线路潮流相结合来判断当前时刻各线路的故障状态。由于台风由远及近的过程中台风对电网的影响程度不断变化，且不同线路故障对电网带来的影响大小是重要评估因素，将台风故障率及线路电气介数加以随台风移动而变化的权重，作为评估线路脆弱度的指标；对传统SOC大停电模型进行改进，与台风天气下的线路故障率相结合。以ND电网为算例进行仿真分析，计算玛莉亚台风侵袭期间该电网随时间变化的线路脆弱度，并对发生的连锁故障进行模拟分析；仿真结果验证了本文建立的模型的有效性，并在工程实践上有一定的应用价值，同时证明了台风天气下电力系统同样具有自组织临界性并更易进入自组织临界态，且可用分维反应电网整体稳定性。本文所建模型可实时对线路脆弱度和电网整体稳定性进行评估，并为事故演化提供预判，在发生强台风的极端天气环境下，为电网调度人员提前预测事故演化范围、合理制定防台措施和应急方案提供重要参考价值。