基于特征参数的聚合物驱开发指标组合预测方法

赵云飞 孙洪国 张雪玲 周丛丛 冯程程 王志新 周子健 李一宇轩

（中国石油大庆油田有限责任公司勘探开发研究院，黑龙江 大庆 163712）

0 引 言

大庆油田聚合物驱自1996年工业化推广以来，实现连续21 a产原油1 000×104t以上，已经建成世界最大的化学驱生产基地。随着工业化进程的推进，开发对象由一类油层转向二类油层，甚至储量品质更差的三类油层。一类油层与早期开采二类油层聚合物驱开发效果平均提高采收率幅度达到14百分点，但是目前投注区块受储层物性差、剩余油分散、开发方式多样等因素影响，提高采收率幅度差异大，开发指标预测精度越来越难以满足生产需求。

聚合物驱常用的指标预测方法主要分为2类。一类是油藏工程方法［1⁃5］，利用油藏工程原理，建立驱替过程的状态和运动方程，通过离散、差分求解，得到产油量、含水率等开发指标随开采时间的变化关系［6］。此类方法的集成应用是数值模拟技术，目前数值模拟是聚合物驱开发方案编制的基础，但是，需要通过建立地质模型、跟踪水驱拟合，工作量大、耗时长，无法满足聚合物驱快节奏开发调整需要。另一类是数理统计方法［7⁃11］，主要通过确定开发指标的主控因素建立开发指标与影响因素间的回归关系。此类方法的关键是回归关系式的相关系数，为了提高回归关系式的相关度，引入的神经网络，支持向量机等机器学习方法［12⁃15］。这种数理统计预测方法能够方便快捷地预测开发指标的关键参数，但开发指标随注入时间的变化需要建立预测模型。预测模型表征驱替过程的合理性和匹配程度也直接影响开发指标的预测精度，因此，数理统计方法一直受到预测模型和关键点确定方式的双重困扰。

从最早的“模式图”法到应用最多的类比法，再到目前的特征点定量预测法，都在努力探索以区块为研究单元的小样本与高精度、方便快捷之间的平衡。

本次以聚合物驱注入站为研究单元，首先是扩大了样本数量，其次把聚合物驱地下驱替介质的渗流规律与地面阶段采出程度变化规律相融合，建立了采油量生长曲线特征参数与聚合物驱阶段采出程度的关联关系，明确了特征参数的物理意义。针对大庆油田二、三类油层区块，分别给出了以注入速度为核心的采油量和阶段采出程度预测模型，从而实现驱替全过程开发指标精准预测，为油田开发规划编制与开发调整提供技术支持。

1 聚合物驱开发规律及其影响因素

油田开发实践表明，地下驱替介质的渗流规律决定着开发指标的宏观变化规律。根据水驱后聚合物驱的相渗曲线最新研究结果［16］，随着聚合物溶液的注入，油层中聚合物不断增多，驱替相的黏度不断增大，相对渗透率不断降低，油相的相对渗透率逐渐增加，可形成稳定的黏度场，此时“油墙”形成，并形成一次稳定驱替，此时相对渗透率比值呈现直线关系。随着聚合物溶液的突破，“油墙”逐渐被采出，含水率快速上升，油相相对渗透率逐渐在另一水平稳定下来，形成二次稳定驱替（图1）。

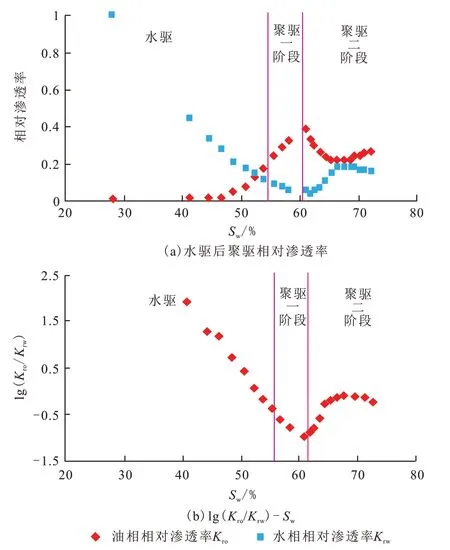
图1 聚合物驱相对渗透率与含水饱和度关系Fig. 1 Relationship between relative permeability and water saturation of polymer flooding

由一、二类油层聚合物驱（统计15个一类油层和22个二类油层区块）开发指标变化趋势来看，区块含水率、阶段采出程度指标变化特征与相渗曲线变化特征具有较好的一致性。整个开采过程可以划分为4个阶段：含水率下降油墙形成阶段、含水率低值油墙稳定驱替阶段、含水率回升油墙突破阶段和含水率稳定油墙采出阶段。体现在阶段采出程度与注入量关系曲线上，含水率低值稳定驱替和含水率稳定油墙采出2个阶段呈现较好的线性规律，而含水率下降油墙形成和含水快速回升油墙突破阶段由于不稳定驱替，直线关系拟合度不好，呈弧状变化（图2）。

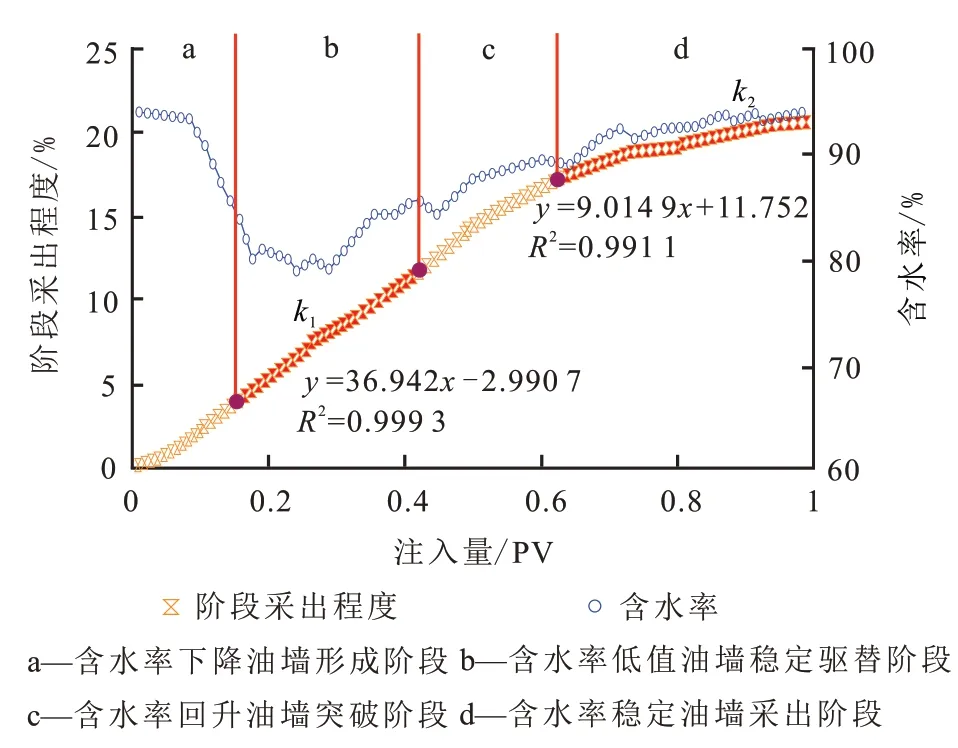
图2 聚合物驱开采过程阶段划分Fig. 2 Stage division of polymer flooding process

其中，第1直线段（k1）起点为0.10~0.25 PV，平均为0.16 PV；终点为0.25~0.50 PV，平均为0.38 PV；斜率为20~40。第2直线段（k2）起点为0.55~0.80 PV，平均为0.65 PV；终点为0.95~1.00 PV，平均为0.99 PV；斜率为10~20。第1直线段斜率为第2直线段斜率的2倍以上，反映了第1直线段为含水低值阶段，是主要增油阶段。因此，如果确定出2个稳定驱替阶段的起始点及直线斜率，便可量化表征聚合物驱全过程阶段采出程度指标。借鉴已有开发效果影响因素研究成果［17］，统计了矿场油层有效厚度、油层渗透率、渗透率级差、注聚前初含水率、聚驱控制程度、注入速度及注入浓度7项参数（表1）。将稳定驱替阶段的斜率、采出程度分别与影响因素作相关度分析。

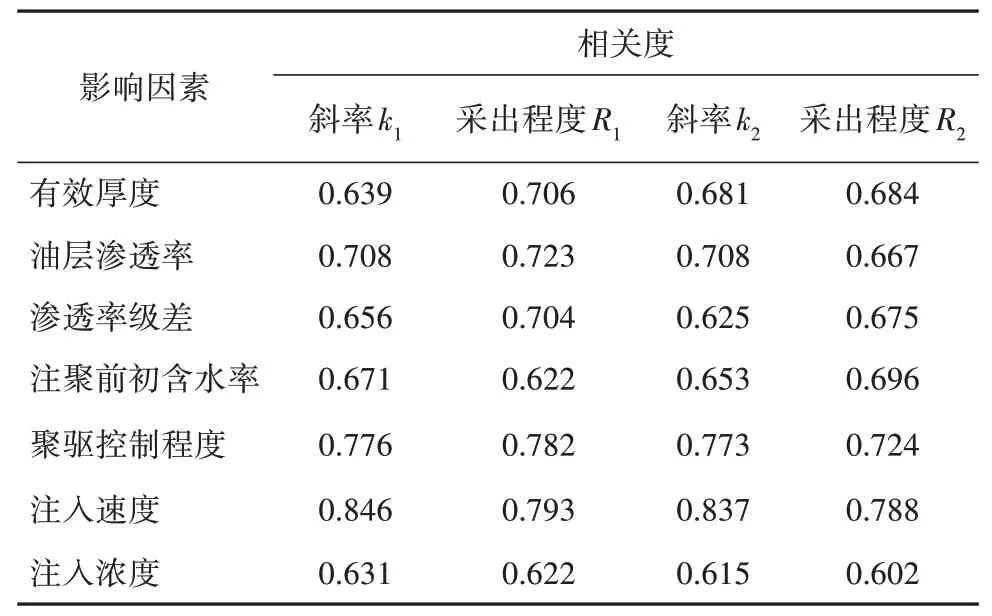
表1 影响因素与关键参数的相关度Table 1 Correlation of influencing factors and key parameters

从分析结果看，区块注入速度、油层渗透率、聚驱控制程度3项因素相关系数在0.600以上，是开发规律变化的主控因素。其中，由于注入速度是油层条件、注采井距、注入浓度和油层驱动压力系统的综合性指标，从注入速度与2条直线斜率的散点图（图3）可以看出，注入速度与稳定驱替直线段斜率具有较高的拟合度，注入速度越大，斜率值越小，增油效果越差。

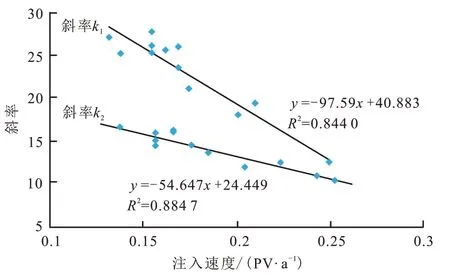
图3 注入速度与稳定驱替直线段斜率的拟合关系Fig. 3 Fitting relationship of injection rate vs. slope of straight line segment of stable displacement

2 预测模型

2.1 产油量预测模型

聚合物驱产油量经历上升、稳定、递减甚至衰减的过程（含水形态与其相反），其形态符合生长曲线形态［18］。常用的生长曲线主要包括Weibull、Logistic及Gopertiz 3种模型，其中，Weibull模型不存在极限值，不适合表征累产油量曲线；Gopertiz模型存在极限值但其导数曲线具有对称性，不适合表征聚驱瞬时产油量；Gopertiz模型存在极限值且其导数呈现非对称性特征，适合表征累计和瞬时产油量。因此，本文采用Gopertiz模型，通过明确其中参数的物理意义，建立各参数量化表征模型，确定分类油层聚合物驱全过程产量。

Gopertiz模型表达式为

变换为对数形式

式中：R——聚合物驱阶段采出程度，%；

vi——注入速度，PVa；

a，b，c——模型特征参数；

t——注入时间，a。

由式（2）可以得出，当vit趋于无穷大时，a≈R，即参数a的物理意义为聚合物驱阶段采出程度；当ln[ln(R/a]=0时，vit=b/c，为含水率最低点，即为最大增油量点。

因此，将聚合物驱阶段采出程度预测与产油量模型特征参数联合，通过总量控制全过程的采出程度明确含水最低点位置，便可实现产油量全过程量化表征。为了验证模型的适应性，编制了特征参数a、b、c拟合程序。对大庆油田二类油层66个注入站实际开发数据进行拟合（表2），通过机器学习，拟合度均在0.995 5以上，表明该模型可精确量化表征聚合物驱的全过程产油量。

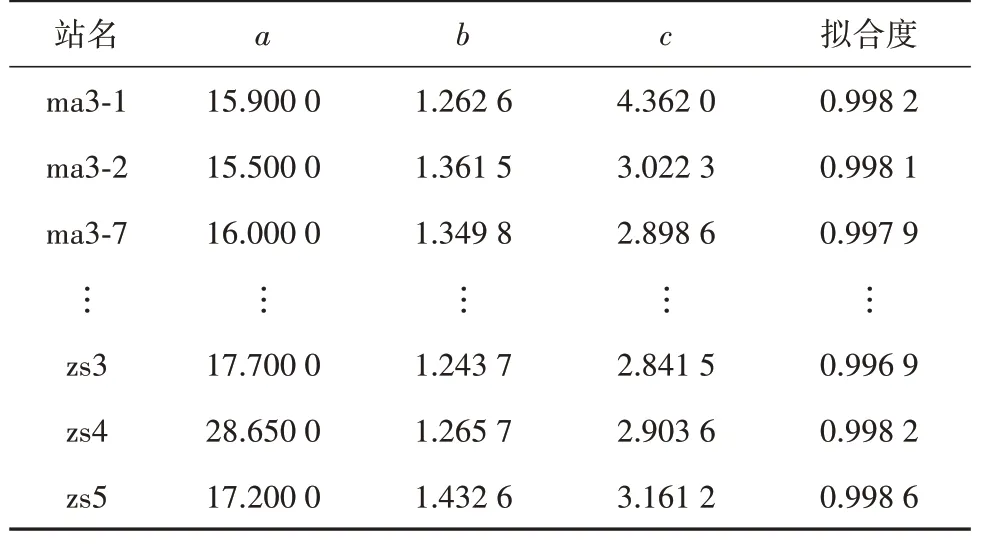
表2 特征参数拟合结果Table 2 Characteristics parameters fitting results

2.2 特征参数预测模型

3个特征参数的确定是该方法的关键。特征参数a参照聚合物驱分阶段采出程度确定；特征参数b根据拟合结果，由不同开发区开发效果分类结果直接确定；特征参数c依据分类标准，分析影响因素，建立分类函数确定。具体计算流程如图4所示。

图4 特征参数确定流程示意Fig. 4 Schematic workflow of characteristics parameters determination

2.2.1 特征参数a

特征参数a为聚合物驱阶段采出程度。由聚合物驱不同阶段的变化规律及影响因素分析，特征参数a预测模型可以表示为

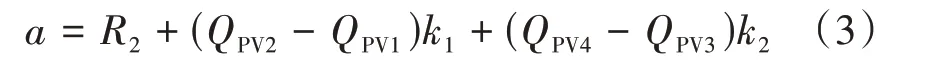
式中：a——聚合物驱阶段采出程度，%；

R2——第2直线段起点的采出程度，%；

QPV1——第1直线起点注入量，PV；

QPV2——第1直线终点注入量，PV；

QPV3——第2直线起点注入量，PV；

QPV4——第2直线终点注入量，PV；

k1——第1直线段斜率；

k2——第2直线段斜率。

为了减少不同开发方式对阶段采出程度的影响，将大庆油田4大开发区的66个注入站进行地质分类。利用大数据分析技术，分别建立了采出程度各阶段关键参数的拟合函数（表3）。根据不同油层不同注入速度下的阶段采出程度分阶段计算，最终得到特征参数a。

表3 阶段采出程度关键参数拟合函数统计Table 3 Statistics of fitting function of key parameters of stage recovery percent(OOIP)

2.2.2 特征参数b和c

特征参数b和c为机器学习的拟合值。同样将大庆油田4大开发区的66个注入站进行地质分类，然后，利用大数据分析技术得到了b和c的确定方式（表4）。同一开发区b值趋于恒定，由地质分类结果可直接确定；特征参数c值依据分类标准，建立了分类函数，由单位注入体积的采出程度的拟合函数确定。

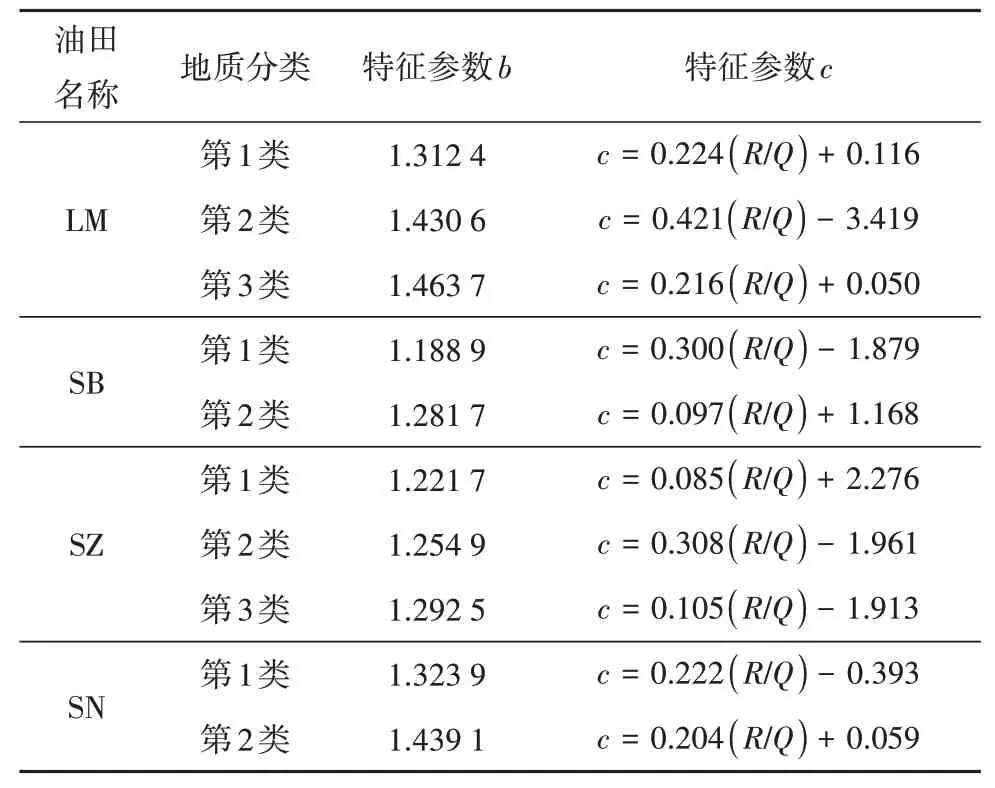
表4 特征参数b与c确定方法Table 4 Determination method of characteristics parameters b and c

3 应用实例

以LM油田第一类区块开发指标预测为例，说明特征参数和全过程产油量预测模型的确定方法。根据表3统计的不同油层类型大数据回归结果，LM油田第一类区块阶段采出程度第1段直线起点注入量0.15 PV，起点采出程度2.5%，终点注入量0.30 PV，由斜率1的回归公可以得到注入速度为0.12、0.14、0.16 PV/a时的斜率值。由表3斜率2和起点采出程度回归公式以及公式（3），可以确定出第2直线的起点采出程度和斜率值以及结束点的采出程度。由第1直线段的结束点和第2直线段的起始点，得到含水回升阶段近似直线段的斜率，进而计算出阶段采出程度随注入量的变化，最后，得到LM油田第一类区块不同注入速度下阶段采出程度的全过程变化（表5）。结束点的采出程度对应含油量模型特征参数a值。

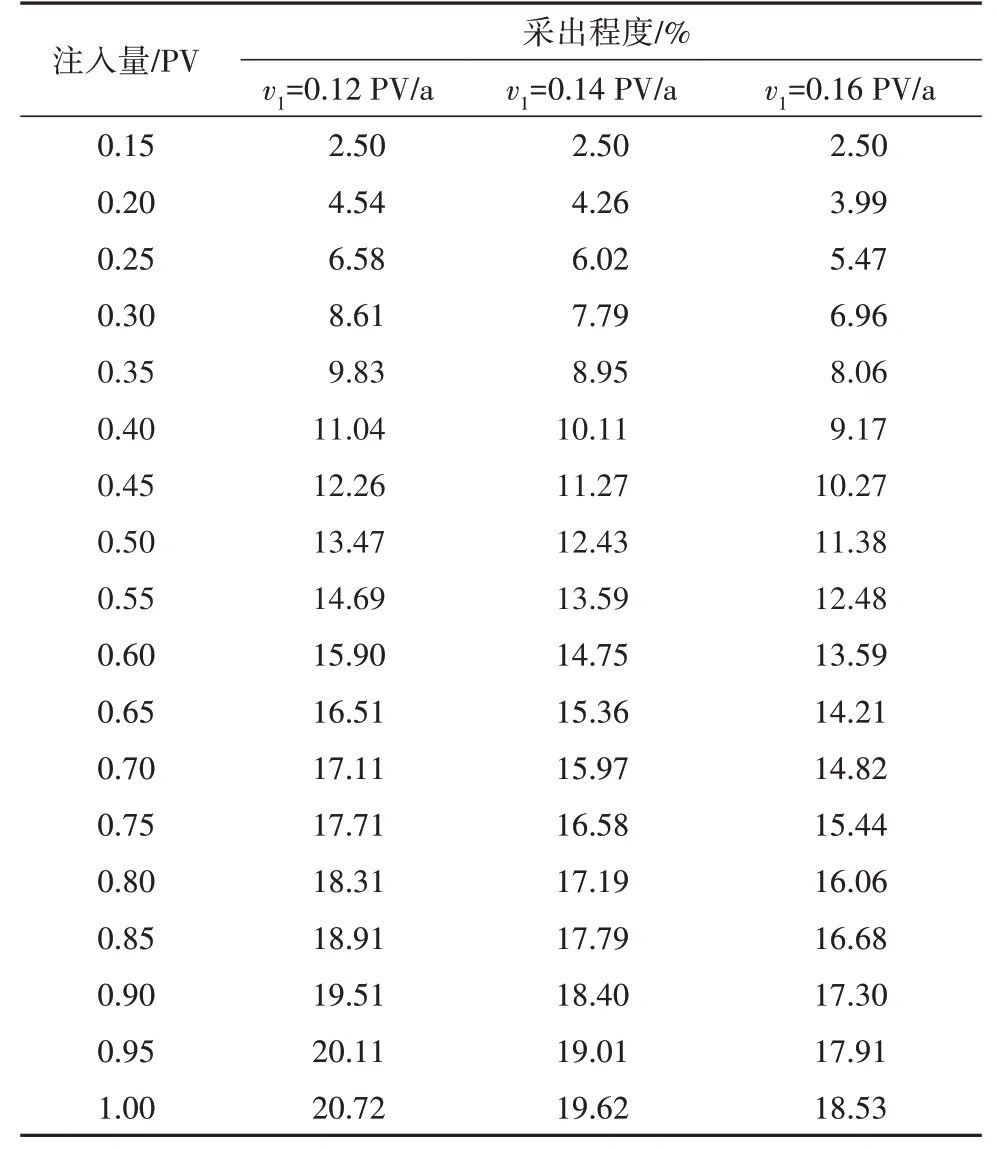
表5 LM油田第一类区块阶段采出程度Table 5 Stage recovery percent(OOIP) of Class 1 block in LM oilfield

根据区块地质分类和数据拟合结果，特征参数b值选取各类拟合参数的算术平均值1.312 4；特征参数c依据单位体积采出程度拟合关系c=0.224 5×（R/Q）+0.116求得。最终对LM油田的BBK区块在注入速度0.14 PV/a的产油量和阶段采出程度全过程变化动态进行了预测。

按照同样的步骤，对大庆油田4大开发区的不同聚合物驱区块分别进行了预测（图5）。由模型预测结果与实际开发曲线对比可知，模型预测符合率均在90%以上，能够满足年度及长远开发规划编制需求。基于特征参数的开发指标组合预测方法可以为二、三类油层聚合物驱中长期规划编制和开发方案调整提供技术支持。

图5 模型预测与实际开发曲线对比Fig. 5 Comparison of model prediction and actual development curve

4 结 论

（1）大庆油田聚合物驱区块多、井数多，使得探索基于大数据分析技术的开发指标预测方法成为可能。本文从聚合物驱微观渗流规律与宏观开发指标相结合为出发点，实现从开发机理角度对聚合物驱全过程进行阶段划分，明确各特征点和驱替特征曲线，为开展全过程开发指标定量表征奠定理论基础。

（2）影响聚合物驱开发效果的因素多而复杂，应用矿场统计和相关性分析方法，对以注入站为研究单元的动态数据进行影响因素分析，确定出以注入速度为核心的主控因素，并且利用大数据学习，给出了不同地质分类的阶段采出程度逐段分解的回归函数。

（3）引用生长曲线法建立聚合物驱产油量预测模型，实现其应用领域的拓展。通过编制计算机程序，实现模型与实际开发数据的动态拟合，拟合精度在0.99以上，该方法具有较强的适应性。同时，通过大量数据拟合和验证，建立模型特征参数与聚合物驱驱替过程的关联性，使其具有明确的物理意义，实现数理统计与油藏工程的深度结合。

（4）应用上述方法分别对大庆油田4个开发区4个典型区块开展产油量预测，模型预测符合率均在90%以上，能够满足年度及长远开发规划编制需求，且方法思路可为同类油田开发指标预测提供借鉴。