冻结裂隙砂岩解冻后蠕变力学特性研究
2023-02-13任建喜曹西太郎云梦晨
任建喜,张 凡,曹西太郎,张 琨,云梦晨
(1.西安科技大学 建筑与土木工程学院,陕西 西安 710054;2.北京工业大学 城市建设学部,北京 100124)
陕北地区是中国14个重要煤炭生产基地之一,特别是榆横四期许多新的千万吨级现代化煤矿需要建设,其赋存煤炭资源的地层包括富水中生界白垩系洛河组砂岩地层,该地层岩性为发育大型交错层理的细粒、中粒长石砂岩,具有弱胶结及易风化大孔隙的特点[1-3]。为了保证在富水的洛河组砂岩地层中凿井安全顺利施工,需采用人工冻结法施工。冻结斜井解冻后井筒围岩的蠕变损伤力学特性是影响斜井井筒长期稳定性的重要因素之一,在长期应力作用下控制井筒和围岩体的变形及裂纹扩展是保证斜井安全使用的关键。
开展解冻后裂隙岩体蠕变作用下的力学性能研究,需大量含不同裂隙倾角的岩样。而现场采样会面临如研究费用高、条件复杂以及釆样周期长等问题[4],取得的原岩岩样均质性也难以保证。因此,许多学者选择使用类岩材料来研究裂隙节理岩体的损伤演化规律[5-7]。目前国内外学者对裂隙岩石的力学性质和蠕变特性等方面也进行了大量的试验研究[8-12]。在此基础上,杨超等[13]研究了卸荷条件下裂隙岩体的蠕变特性,提出了裂隙岩体损伤蠕变模型,并与室内试验结果进行了对比与分析。杨昊等[14]研究不同条件对单裂隙岩体力学特性的影响发现裂隙倾角对岩体强度影响最大。为了研究冻融作用对岩体损伤特征的影响,张慧梅等[15]研究了冻融和荷载作用下损伤模型;裴向军等[16]研究饱和度对裂隙岩石的冻融特征的影响。
上述的研究大多集中在常规裂隙岩体蠕变特性或冻融作用下裂隙岩体的损伤模型,对于冻融作用后不同裂隙倾角的三轴蠕变特征及蠕变模型则少有研究。本文以陕西省榆林市可可盖煤矿冻结斜井工程为依托,开展类裂隙砂岩解冻后三轴压缩蠕变特性试验研究,并根据试验结果建立考虑原生节理影响的非线性蠕变模型并且进行三维推广,该研究为人工冻结斜井井筒长期稳定性评价及矿井安全生产提供一定理论参考。
1 类裂隙砂岩试件的制备
利用陕西省榆林市可可盖煤矿洛河组砂岩岩芯制作尺寸为∅50mm×100mm的圆柱状国际标准试件。使用型号为XRD-7000S的X射线衍射仪进行砂岩物相组成成分的半定量分析。分析得洛河组砂岩主要由含量较多的石英及长石组成,其中石英含量为52%,钙长石含量为23.5%,钠长石含量为3.4%。另外存在其他含量较低的金属离子杂质。
通过分析配比材料对类砂岩强度的影响程度完成了配比正交试验,共制备了9组不同配比的试验件。开展不同配比的类砂岩单轴压缩试验,并对试验结果进行方差分析,得到最优配合比为:硅酸盐水泥∶石膏粉∶石英砂∶用水量=6∶1∶2∶3∶3。
洛河组砂岩和类岩强度及变形指标见表1,根据岩石相似理论分析,砂岩和类岩材料的物理力学参数比较接近,且基本满足主要相似常数的关系。因此,相似材料基本满足相似定律的要求。
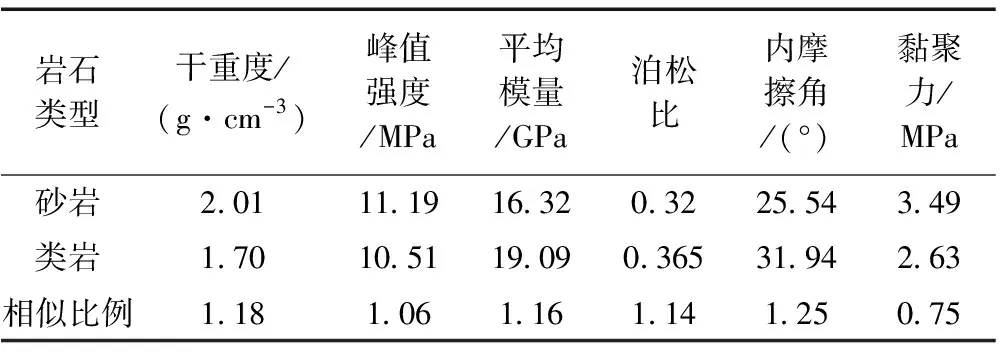
表1 洛河组砂岩及类岩相似比尺
本文所用类裂隙岩石的预制裂隙为微张裂隙(缝长20mm,宽为1.5mm),制作与水平夹角为0°、45°及75°三种倾角的试件,如图1所示。

图1 不同倾角类岩标准试件
2 三轴压缩蠕变试验方案
根据现场工程背景条件,首先进行冻结温度为-10℃、解冻温度为30℃,冻结时间为48h的冻融试验。然后对解冻后各倾角类裂隙岩石开展围压2MPa三轴压缩试验,为蠕变试验提供基础参数。
三轴压缩蠕变试验采用TAW-1000微机控制高温三轴蠕变试验机,采用围压及轴压为速率0.05MPa/s(3MPa/min)的应力控制方式,根据解冻后各倾角类裂隙砂岩三轴峰值强度的20%、40%、60%及80%分四级进行蠕变加载,蠕变加载每一级蠕变时间为12h,当上一级蠕变量趋于稳定后进入下一级蠕变荷载,由小到大逐级加载轴压直至试件破坏,具体加载方案见表2。
3 三轴压缩蠕变试验结果分析
3.1 不同倾角类裂隙岩石解冻后轴向蠕变曲线
将各倾角类裂隙岩石解冻后全过程蠕变曲线按陈氏加载法处理为分级加载蠕变曲线,如图2所示。裂隙岩石在每一级荷载作用下首先短时间内产生较为明显的瞬时应变,随后会出现一定的增长滞后现象,最后会经历蠕变速率不断下降趋近于0的稳定蠕变阶段。荷载等级越高,岩石进入稳定蠕变阶段所经历的时间就越长,这说明随着荷载等级的提高,岩石的粘滞性表现也越明显。随着施加蠕变应力水平的增加,蠕变曲线斜率会逐渐增加,由稳态蠕变阶段逐渐向亚蠕变阶段过渡,在此时岩石发生局部破坏产生了塑性变形。随着施加的应力水平等级持续增加至超过加速蠕变阈值时,蠕变曲线会在短时间内迅速上升,蠕变速率及蠕变变形量会猛增,岩石被破坏。

表2 解冻后各倾角类岩蠕变试验分级加载量

图2 各倾角类岩解冻后轴向蠕变曲线
裂隙岩石解冻后分级加载蠕变速率曲线如图3所示。随着荷载等级的增加,瞬时速率先增大,随后进入速率逐渐减小的蠕变衰减阶段,最后为蠕变速率逐渐减小趋近于0进入蠕变稳定阶段。在长期荷载作用下,每一级蠕变荷载下瞬时蠕变速率在增加,并且倾角为45°时蠕变速率为不同倾角中蠕变速率最快的。

图3 各倾角类岩解冻后轴向蠕变速率曲线
根据各倾角类裂隙岩石解冻后轴向蠕变曲线与轴向蠕变速率曲线得到每级蠕变荷载的稳态蠕变量与稳态蠕变速率随裂隙倾角及荷载等级的三维曲面变化,如图4及图5所示。可看出随着蠕变荷载等级的逐渐增加产生的瞬时蠕变量也在增加,说明随着轴向长期荷载值的加大裂隙岩石的内部裂纹的扩展程度与贯通程度也在加剧。随着轴向长期蠕变荷载的增加,θ=45°的裂隙岩石瞬时蠕变量增加的最多,其次是,θ=0°时,最后为θ=75°时。这说明在长期荷载作用下,45°倾角试件内部新生裂纹沿着预制裂隙发育与扩展程度更大,产生的轴向蠕变量更多且变化速率更快。因此,对受长期荷载影响的冻结斜井工程,应充分考虑裂隙围岩受蠕变特性与裂隙展布特征,根据围岩裂隙角度制定受力与变形预警值,确保围岩受力低于长期强度,变形低于蠕变极限,同时通过实时监测受荷影响较大处,对冻结斜井工程进行安全评估。

图4 稳态蠕变量随荷载等级及裂隙倾角的变化

图5 稳态蠕变速率随荷载等级及裂隙倾角的变化
3.2 类裂隙砂岩解冻后破坏特征分析
各裂隙倾角类砂岩解冻后蠕变破坏情况如图6所示。可看出当裂隙倾角为0°时类裂隙岩石试件的蠕变破坏模式为沿着预制裂隙产生次生主裂纹最终贯通形成主断裂面,进而造成试件力学性能的破坏。当裂隙倾角为45°及75°时类裂隙岩石试件的破坏模式为典型的剪切滑移破坏。试件出现鼓状变形,即试件中间较宽两端较窄。这是由于在长期应力作用下次生主裂纹周围破碎的颗粒重分布与新产生的破碎颗粒进行粘合。

图6 解冻后各裂隙倾角类岩蠕变破坏情况
4 考虑裂隙岩石原生节理影响的非线性蠕变本构模型
4.1 裂隙塑性体元件
对于洛河组砂岩这样原生节理较为发育的软岩而言,存在一门槛应力值,当低于这一应力值时岩石微裂隙的压密闭合现象不明显,宏观的瞬时塑性变形未产生;当应力达到这一应力值时微裂隙压密闭合而导致的塑性变形逐渐增加。故根据陈沅江等[18]的研究,引入一种将2个等截面悬臂梁在零曲率处相连组成双悬臂梁模型,并且与圣维南体并联的裂隙岩石塑性元件。应力为σ时蠕变状态方程为:
式中,σ为蠕变荷载强度,MPa;σs为岩石长期强度即蠕变强度,MPa;σS1为产生瞬时塑性应变的应力阈值,MPa;σL为裂隙闭合变形量为75%的有效应力,MPa;εL为最大瞬时塑性变形量,%。其力学模型如图7所示。

图7 裂隙塑性体力学模型
4.2 蠕变全过程劣化演化方程
运用损伤力学模型来刻画岩石蠕变变形规律的研究,提出可以描述岩石减速蠕变及等速蠕变的蠕变劣化演化方程,其形式为:
D=1-exp(-m·ε)
(2)
式中,m为材料常数。
由于(2)式描述不了蠕变加速阶段,为了能描述蠕变加速阶段,引入通过劣化因子的概念推导出的蠕变全过程劣化演化方程并做处理:
式中,t*为岩石发生急速蠕变的时刻;A、N为材料常数。
当岩石达到蠕变寿命tf(h)时,岩石劣化发展到断裂状态,蠕变损伤变量D=1。在此时则有:
即
整理之后可得到蠕变损伤变量表达式为:
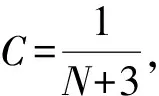
式中,ε*为t*时刻所对应的应变值,而tf、t*、ε*均可以从蠕变试验中直接获取,参数C和m为材料常数。
4.3 考虑原生节理影响的非线性蠕变模型建立
本文所建立的考虑原生节理影响的非线性蠕变模型是在经典西原体模型基础上,加入考虑原生节理影响的裂隙塑性体元件,将整个蠕变过程分为四个阶段。其力学模型如图8所示。

图8 考虑原生节理影响的非线性蠕变组合力学模型
由元件间串联性质可知总应力与各串联体应力相同,总应变为各串联体应变之和,可表达为:
式中,σ1、σ2、σ3、σ4、ε1、ε2、ε3及ε4分别表示各串联体的应力及应变。
根据本构方程进行Laplace变换后,将蠕变全过程劣化演化方程通过有效应力的基本概念引入蠕变模型中,本构蠕变方程一维形式如下:
1)当σ<σcr时,
ε=σ/E0
(9)
2)当σS1≤σ<σcr时,
3)当σcr≤σ<σs时,
4)当σ≥σs时,
式中,E0可表示为岩石的瞬时弹性模量;σS1为产生瞬时塑性应变的应力阈值;E1可表示为岩石的黏弹性模量;η1,η2可表示为凯尔文体与理想黏塑性体的粘滞系数,GPa·h;σcr为岩石蠕变的起始应力;σs为岩石的长期强度;D为劣化演化方程。
4.4 非线性粘弹塑性蠕变模型的三维推广
在蠕变过程中,一般可认为应力球张量作用影响远小于应力偏张量的影响,因此可以取广义Mises中的Druck-Prager屈服函数作为三维黏弹塑性体的屈服函数,通常形式可表达为:
可假设岩石的初始屈服函数值为1,根据关联流动法则定义,可取Q=F,则上式可表达为:
本文所采用的室内岩石三轴压缩试验为假三轴压缩试验,即主应力σ1>σ2=σ3,则:
将上式代入式(9)—(12)中,可得到三轴作用下类裂隙岩石非线性蠕变模型三维推广形式:
1)当σ1-σ3<σS1时,
2)当σS1≤σ1-σ3<σcr时,
3)当σcr≤σ1-σ3<σs时,
4)当σ1-σ3≥σs时,
4.5 参数确定方法及验证
当施加在试件上荷载等级大于蠕变长期强度并且蠕变变形充分发展时,试件会出现蠕变第三阶段蠕变加速阶段,此时曲线呈现出非线性特征。根据式(17)—式(20)进行分段求解。根据相关研究可知岩石蠕变长期强度一般为常规三轴强度的70%~80%之间,本文选取常规三轴强度的70%作为岩石蠕变的长期强度。裂隙倾角0°时第四级荷载下蠕变曲线如图9所示,根据增长曲线可看出试件经历蠕变速率衰减的减速阶段,蠕变速率恒定的蠕变稳定阶段及蠕变速率突增的蠕变加速阶段,因此可以找到蠕变开始点O、蠕变稳定阶段开始点A、蠕变加速阶段开始点B及蠕变试件破坏时间点C。找出的三个蠕变特征点A、B及C,可对应蠕变全过程劣化演化方程中D(t)的t1、t*及tf。即时间区段(0,t1)为蠕变减速阶段,(t1,t*)为蠕变稳定阶段、(t*,tf)为蠕变加速阶段,可以运用最小二乘法的L-M优化算法进行求解出参数。

图9 裂隙倾角0°第四加载阶段蠕变量及蠕变速率图
依据上述模型参数识别方法得到的模型参数见表3,利用得到的模型参数得到实验数据散点图及拟合曲线,如图10所示。通过引入时效损伤因子,解决由于时效原因带来的曲线非线性问题,并且通过引入裂隙塑性体可以解决由于预制裂隙的存在而导致瞬时蠕变阶段产生的瞬时塑性非线性蠕变变形的问题,模型拟合数据基本与试验数据吻合。

表3 解冻后不同裂隙倾角类岩非线性蠕变模型参数

图10 各裂隙倾角类岩解冻后试验散点及拟合曲线
5 结 论
1)随着蠕变荷载的增加,产生的瞬时蠕变量也在增加。在类裂隙砂岩中预制的三种倾角中,倾角为45°时产生的瞬时蠕变量最大,其次是0°时,最后是75°。说明在长期荷载作用下,倾角45°时类裂隙岩石内部新生裂纹沿着预制裂隙发育与扩展程度更大,产生的轴向蠕变量更大且变化速率更快。
2)基于西原体蠕变模型,通过引入裂隙塑性体元件及蠕变全过程劣化演化方程建立考虑原生节理影响的非线性蠕变模型并且进行三维推广。依据分级加载三轴压缩蠕变试验数据对三维应力状态下的非线性蠕变模型中的参数利用最小二乘法进行求解并拟合,拟合结果与试验数据基本吻合。
