基于双平方根算子的速度建模方法及应用

2023-02-12阿力甫江热合木吐力潘龙李献民林娟马晶晶窦强峰

新疆石油地质 2023年1期

阿力甫江·热合木吐力，潘龙，李献民，林娟，马晶晶，窦强峰

(中国石油新疆油田分公司勘探开发研究院地球物理研究所，乌鲁木齐 830000)

准噶尔盆地南缘地表条件和地下构造十分复杂，给地震勘探带来了很大的困难[1]。由于地表起伏剧烈，地下速度横向变化大，基于常规浮动面的叠前深度偏移技术，在南缘的应用受到一定的限制，起伏地表叠前深度偏移技术成为提高该地区成像精度的首选。起伏地表叠前深度偏移技术的偏移面建立在地表一致性浮动面上，充分考虑了炮点和检波点随地表高程的变化趋势，是接近真地表的一种偏移成像方式，比常规共中心点道集面的叠前深度偏移更具优势，可提高成像效果[2-3]。

但是以往的起伏地表深度偏移技术也存在一些不足。由于起伏地表叠前深度偏移的初始速度模型及偏移前道集都是通过时间域处理得到的，而现有的时间域处理多在共中心点道集面上进行，导致深度域与时间域的处理基准面不统一，从而造成时间域静校正量与道集不匹配，无法对偏移前道集进行高频时差校正，同时也造成时间域得到的速度与道集不匹配。因此，用时间域得到的速度作为起伏地表叠前深度偏移的初始速度模型时，模型精度较低，影响深度域偏移成像效果。

1 研究思路

针对起伏地表叠前深度偏移技术存在的不足，本文利用双平方根算子的高精度速度建模方法，建立了基于双平方根算子的叠前深度偏移流程(图1)，从时间域引入双平方根算子，确定起伏地表基准面，把偏移前道集校正到起伏地表基准面，进行起伏地表叠前时间偏移处理，从而实现时间域和深度域基准面的统一，解决与静校正量道集不匹配及速度与道集不匹配的问题，为起伏地表叠前深度域高精度速度建模提供资料。

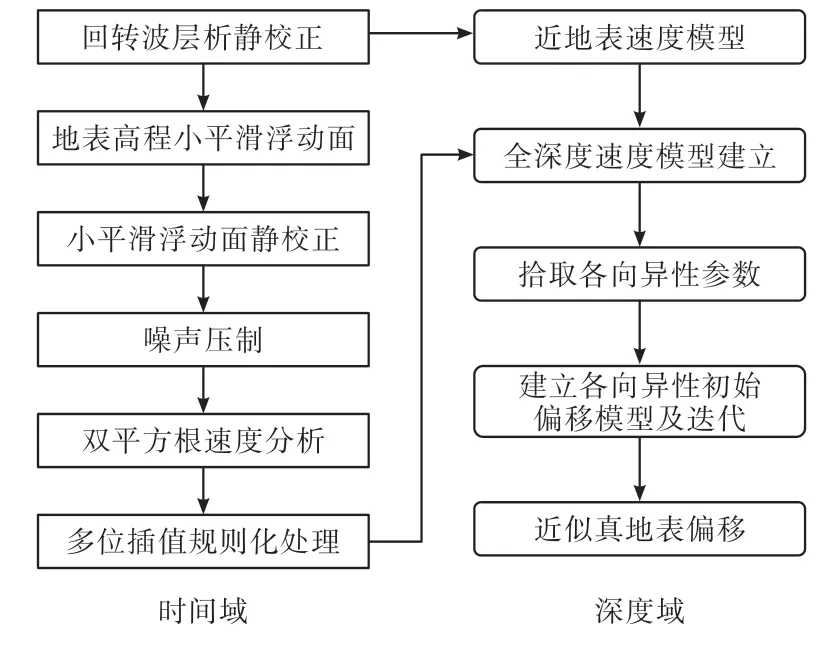
图1 叠前深度偏移新流程Fig.1.New process of pre-stack depth migration

新流程比常规流程更具有优势：①新流程基于双平方根地表一致性时间域处理得到的地表小平滑浮动面，与深度偏移采用的浮动面一致；②静校正模型与近地表速度模型完全吻合，消除静校正误差；③深度域速度模型精度较高，保留了井数据的高频信息和速度趋势。

2 关键技术

2.1 双平方根算子

常规叠加建立在水平层状介质及横向速度连续变化的假设上，不适用于地形复杂和横向速度剧烈变化的区域。构造起伏较大时，时距曲线和水平动校正方程相差很大，同一共中心点道集在相同界面上的反射点位置分散。准噶尔盆地南缘地表和地下条件复杂，地震波速度变化剧烈，常规叠加偏移处理成像效果差[4]。

Kirchhoff 叠前深度偏移通过地震波旅行时计算和偏移积分求和完成。计算地震波旅行时需要知道炮点和检波点的位置，处理过程中保持炮检点位置真实性，对地震波旅行时计算极为重要。因此，需探索能够适用于地表和地下双重复杂地区的地震波旅行时计算方法。

由于地表高程变化剧烈，导致炮点和检波点的高程差异较大，使得炮点到地下反射点与地下反射点到检波点的路径不对称。因此，在计算地震波旅行时时，不能用常规的单平方根算子，需要一种非水平地表情况下的地震波旅行时计算方法。在Kirchhoff 叠前时间偏移中，地震波旅行时的精度影响成像结果的精度，也影响起伏地表叠前深度偏移初始速度模型的精度。常规Kirchhoff叠前时间偏移中假设地表水平，得到地震波旅行时计算公式[5]：

地表在非水平情况下，炮点和检波点的坐标不再对称。地震波旅行时：

本文讨论非水平地表情况下的地震波旅行时的计算，先将非水平地表数据按射线路径坐标映射到水平坐标上，再在新水平坐标下对地震波旅行时进行计算。在新水平坐标下，用常规Kirchhoff叠前时间偏移的单道偏移算法进行偏移成像，再把成像结果用合适的速度校正到统一基准面上，进行速度分析和叠加成像。在新水平坐标系中，地震波旅行时[6-7]：

利用双平方根算子，可以分别求取地震波从炮点到反射点的走时和从反射点到检波点的走时，比较适合复杂山地区域，突破了地层是水平层状介质的限制。针对起伏地表，双平方根算子动校正比单平方根动校正更精确，可得到更准确的地震波旅行时，提高了起伏地表速度建模的精度和成像质量。

因为引入双平方根算子，在时间域也能实现对起伏地表的地震资料处理，为起伏地表叠前深度偏移提供了统一的处理基准面，时间域得到的速度与偏移前道集匹配较好，为深度域偏移成像提供了准确的资料，可进一步提高深度域速度建模的精度，降低井震误差。

2.2 成像基准面的选择

成像基准面的选择是为了获得最优的速度和成像效果。成像基准面的一个非常重要的作用，就是使偏移速度和真实介质速度模型能够较好地吻合，从而提高偏移速度分析精度，提高起伏地表深度偏移初始速度模型的精度。

成像基准面有2 种[8]。第一种是以炮检点中点高程为成像基准面，新水平坐标系下计算得到的地震波旅行时和实际地表观测得到的地震波旅行时相等，但存在2 个问题：①即使是同一个共中心点道集，每一道都有一个成像基准面，即成像基准面随着道的变化而变化，每一道的时移量都不同，不利于最终基准面上的同相轴叠加处理；②均方根速度是定义在共中心点处的速度，该成像基准面所用的速度与成像深度不对应。第二种是以共中心点高程为成像基准面，此时，存在共中心点高程在炮检点高程之上、之间和之下3 种情况(图2)。根据(5)式，可以计算出这3 种情况下成像基准面上的地震波旅行时。共中心点位置确定之后，对每一道就可以应用常规Kirchhoff叠前时间偏移进行偏移处理。相对于以炮检点中点高程为成像基准面来说，以共中心点高程为成像基准面的方法，同一个共中心点道集中所有道只有一个成像基准面，有利于同相轴叠加，比第一种更合理，因为在偏移中使用的均方根速度是由共中心点道集分析得到，成像基准面如果与共中心点高程不一致，将导致使用的均方根速度在深度上发生变化，不利于同相轴叠加[9-10]。

图2 共中心点与炮检点的位置关系Fig.2.Different positions of CMP and shot

需要进一步说明的是，成像基准面作用于成像域空间，与数据域空间无直接关系。在常规地震资料处理中，固定基准面既是成像基准面，也是数据域零时刻空间位置，同时作用于数据域和成像域。而在起伏地表叠前时间偏移中，成像基准面和数据域零时刻空间位置不一致，将数据中炮点和检波点还原至野外观测点，而不是校正至成像基准面的空间位置上。此时，数据域零时刻空间位置为地表，速度模型精度更高，成像效果更好。

2.3 深度域速度建模

从时间域开始，把偏移前数据校正到起伏地表基准面上，实现时间域和深度域处理基准面的统一，用双平方根算子动校正，得到相对高精度的均方根速度作为深度偏移的初始速度模型；同时，处理得到的剩余静校正量，用偏移数据的道间高频时差校正。再根据时间域得到的数据，开展全深度域速度建模，用回转波层析反演方法得到近地表速度模型，对速度进行融合。最后，根据垂直地震剖面速度和测井速度，得到中—深层速度模型，从而建立全深度域速度模型[11-12]。

2.3.1 近地表速度模型建立

在准噶尔盆地南缘山区，复杂的近地表结构导致静校正非常困难。解决复杂静校正问题最直接的办法是建立或反演得到能准确反映低降速带底界之上表层速度变化的近地表结构模型，层析反演软件是反演表层结构模型的主要工具之一[13]。

通过假设速度随深度线性变化，提出了一种快速回转波近地表建模方法。利用微测井信息约束下的层析初始模型，采用多基准面校正，降低地表起伏对反演结果的影响，提高反演精度。回转波层析的优点是反演计算速度快且稳定，其拟定的射线传播路径与山前过渡区域巨厚低速、高速砾岩等连续渐变介质中的传播路径相吻合，反演结果可靠；其缺点是在反演过程中受初始模型精度影响较大[14]。因此，在进行回转波层析之前，应充分分析区域内的表层结构变化规律，利用钻井、测井等数据，建立初始表层结构模型，尽可能避免由于初始模型误差所导致的反演结果不可靠问题。

从研究区域近地表回转波层析反演模型可以看到，反演结果能够准确地反映出高速砾岩和低速砾岩分布及速度变化范围，与测井速度较吻合，反演精度较高(图3)。

图3 准噶尔盆地南缘地表层析反演模型Fig.3.Surface tomographic inversion model for the southern margin of the Junggar basin

2.3.2 中—深层速度模型建立

对研究区域进行速度反演时，利用约束Dix 反演层速度方法，即通过三维约束Dix 反演层速度创建瞬时速度场，用阻尼最小平方法输入平滑的叠加速度[15]，求出合适的加权因子，使叠加速度的平方倒数误差均匀分布，并与正常剩余时差的分布一致。由伴随矩阵线性方程组确定出需要的层速度扰动，再通过褶积定义平滑层速度，最终得到最优的层速度分布。但在地震资料处理中，速度必须在构造模型的约束下从道集中反演得到，由于地震资料信噪比低，速度反演存在不确定性，成像品质不理想，构造模型难以确定，影响最终速度模型的建立。

在构造模型约束下，可以利用已有的垂直地震剖面速度资料以及钻井资料，约束叠前偏移速度场。在纵向上，通过测井速度约束层速度，形成与测井速度吻合的趋势；横向上，保留地震波速度低频趋势，同时根据层位信息，进行井数据的外推迭代，建立反映空间相对变化关系的层速度场，作为深度偏移的初始层速度模型。

2.3.3 各向异性速度场建立及速度更新

研究区地下地质构造复杂，地表被冲积扇砾岩覆盖，各向异性严重，难以准确成像。本文采用的TTI各向异性叠前深度偏移方法，适用于速度横向剧烈变化的介质，比常规偏移成像的效果好。

建立各向异性场需要4 个参数：表征纵波在垂直方向的变化程度δ，影响偏移深度与井资料的吻合度；纵波各向异性强度ε，表征水平方向与垂直方向速度的差异，决定偏移道集在远炮检距是否校平；TTI各向异性地层的倾角θ和方位角φ，影响成像位置的准确性[16-17]。

首先在井口各向同性道集上拾取参数，然后沿层外推，形成各向异性数据体，建立各向异性初始速度模型。在TTI 各向异性叠前深度偏移基础上，进行参数迭代优化，直到井震误差基本消除，得到最终的各向异性参数，从而得到精度更高的叠前深度偏移成像结果。从校正效果上看，各向异性速度场更新后，道集拉平程度较好，说明拾取的各向异性参数较合理(图4)。将最终速度模型叠合测井速度进行一体化质控，发现更新后的速度曲线与测井速度的吻合度明显提高，进一步证明了最终速度模型精度更高(图5)。

图4 准噶尔盆地南缘各向异性速度场更新前和更新后偏移道集Fig.4.Migration gathers before and after the update of the anisotropic velocity field in the southern margin of the Junggar basin

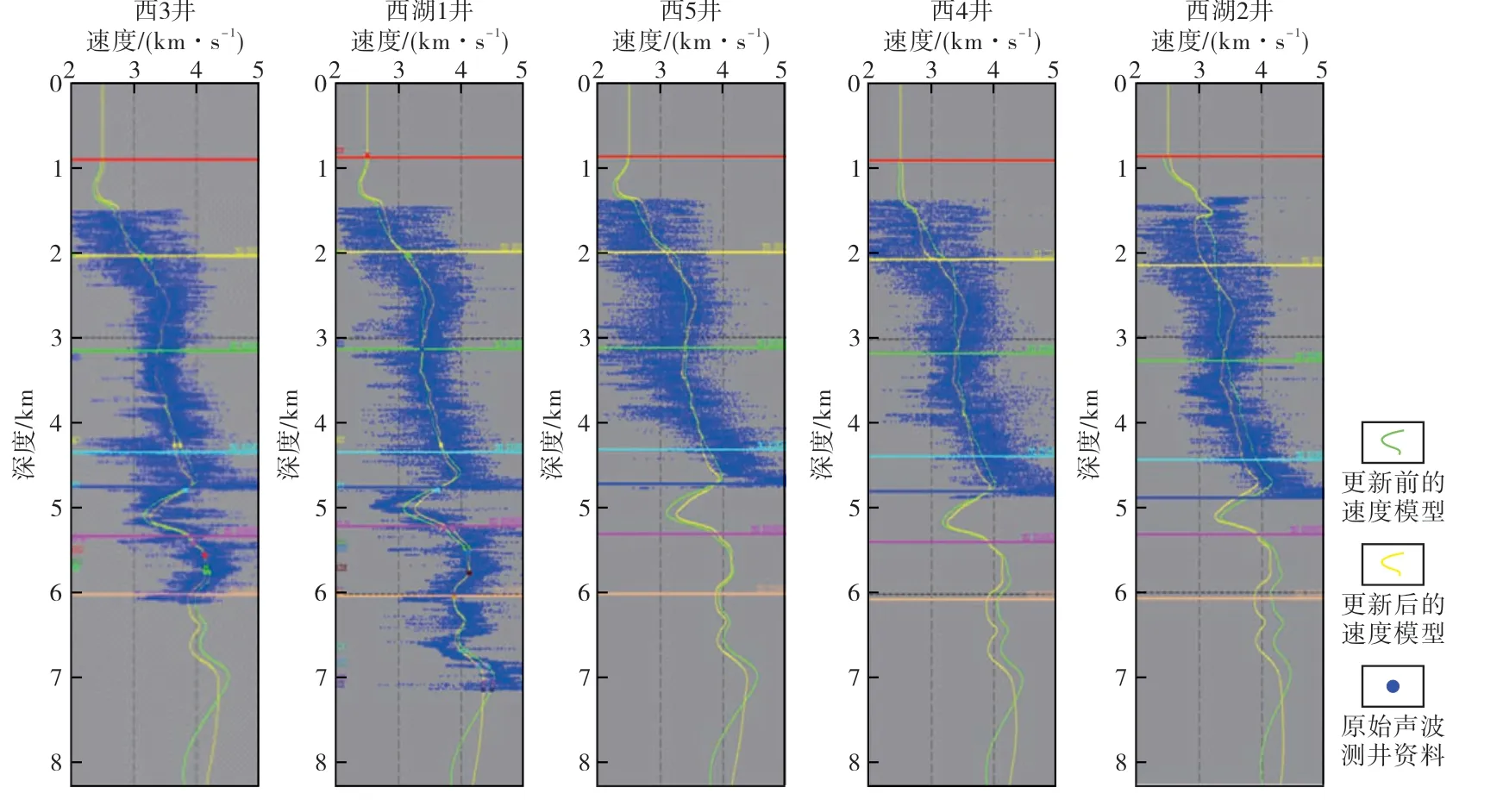
图5 准噶尔盆地南缘更新前后速度与测井速度对比Fig.5.Superimposed display of the model velocity before and after update and the logging velocity in the southern margin of the Junggar basin