基于有效孔隙分布特征的黏土渗透系数公式推导
2023-02-12房营光,徐亚飞,谷任国,2,吴永康
房 营 光,徐 亚 飞,谷 任 国,2,吴 永 康
(1.华南理工大学 土木与交通学院,广东 广州 510640; 2.华南理工大学 亚热带建筑科学国家重点实验室,广东 广州 510640)
0 引 言
流体通过多孔介质的流动称为渗流,在实际工程中出现的管涌、崩岸及深基坑变形等都与土体中渗流有关[1]。土的孔隙特性是影响土体渗透性能的重要因素[2],常用渗透系数反映流体通过孔隙骨架的难易程度。目前岩土工程界有很多关于粗粒土渗透系数的经验公式能够清楚地反映影响渗透系数的主要因素。但是此类公式预测黏性土的效果较差,往往偏差在一个甚至多个数量级。
粗粒土的渗透系数一般远高于黏性土,许多学者为预测其渗透系数做出了大量的努力[3]。Komine[4]考虑膨润土吸水膨胀会改变孔隙结构特性,根据Poiseuille定律,得到了计算膨胀土渗透系数的公式。何俊等[5]考虑渗滤液的离子浓度以及膨润土的孔隙变化情况,结合Poiseuille定律得到了渗透系数计算的改进方法。陈建[6]考虑了黏土孔隙分布特性,对低渗透系数的黏土进行研究,结果发现低渗透系数的黏土孔径分布特殊,渗流行为表现出明显的孔径效应。梁健伟等[7]考虑了极细颗粒黏土的微电场效应,推求了等效渗透系数的表达式。上述研究推理过程物理意义明确,但是公式中的参数不能简便获取,实用性还有待提高[8]。
从以上的研究可以看出,黏土表面双电层形成的结合水膜[9]以及孔隙结构对黏土的渗流特性影响很大。考虑孔隙结构或结合水膜等方面的渗透系数公式,因参数获取不够简便等原因,实用性不强。传统渗透系数经验公式参数简便,却未考虑这两方面[10],从而导致计算值与实际值偏离较大。因此本文的主要目的是考虑黏土孔隙分布特性和黏土表面双电层两方面去修正传统渗透经验公式。首先引入有效流动孔隙概念,即将孔隙流体渗流中贡献最大的那一部分孔隙定义为有效流动孔隙,接着给出黏性土的有效孔隙率的计算方法;然后基于压汞试验的数据,得到黏土微观渗流的有效孔隙分布特征;最后通过试验结果评估未修正及修正后的渗透系数公式的有效性和适用性。
1 斯托克斯孔隙流渗透系数公式
岩土工程界有许多渗透系数经验公式,如太沙基渗透系数公式、柯森-卡门渗透系数公式[11]、斯托克斯孔隙流渗透系数公式[12]等。斯托克斯孔隙流渗透系数公式可由哈根-泊肃叶公式导出。如图1所示,毛细管半径为R,则基于纳维-斯托克斯方程,对于不可压缩流体的定常层流,其运动方程在柱坐标系下的化简表达式为
(1)
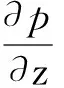
求解式(1) 可以得到渗流速度:
(2)
式中:γw为水的重度,i为水力坡降。
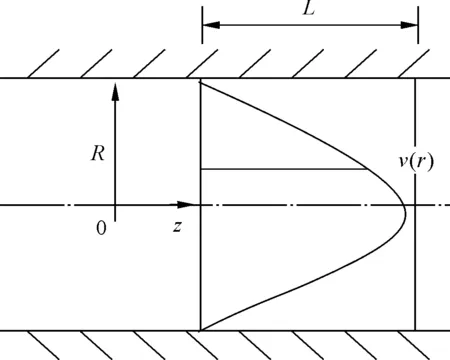
图1 毛细管的渗流模型Fig.1 Seepage model of capillary
进一步假设土体中的孔隙通道是由很多这样的毛细管组成的,土的孔隙率为n,则土体的渗流平均流速为
(3)
式中:r为土体中平均孔隙半径。
则渗透系数k可以表示为
(4)
可以看出斯托克斯孔隙流渗透系数公式是经过较为严格的理论推导出来,物理意义明确。但其推导过程忽略了土的结构性,计算黏土的渗透系数偏差较大。
2 土体渗流的有效流动孔隙
对于渗透性较低的黏土,其渗透性受到孔隙结构的影响十分明显,渗透系数与孔隙度的相关性变差,传统渗透系数经验公式的计算结果往往不太理想。如图2所示,为了定量描述低渗透性黏土孔隙与渗透率之间关系,引入有效流动孔隙概念,即将孔隙流体渗流中贡献最大的那一部分孔隙定义为有效流动孔隙。黏土中还有一部分孔隙由孤立孔隙、半连通孔隙、黏土颗粒表面吸附水占据的孔隙等组成[13]。这些孔隙对渗流没有贡献或者贡献很少,可以认为是无效流动孔隙。因此为了准确预测黏性土的渗透系数,必须考虑无效孔隙的影响,提出一种求解有效孔隙率的方法。

图2 渗流过程中土的几种孔隙Fig.2 Several types of pores in soil during seepage
2.1 孤立孔隙和表面孔隙
压汞试验是测量土的非孤立孔隙分布的一种有效手段,也是一种获取土样微观参数的常用试验方法[14-16]。利用压汞试验探测土的孔隙分布其基本原理是:由于汞是一种非浸润液体,它进入土体孔隙中需要施加外力克服汞的表面张力,即满足杨-拉普拉斯方程。根据这一物理原理,Washburn 给出了进汞压力p与孔隙等效半径r的关系式:
(5)
式中:p为进汞压力,σ为汞的表面张力,θ为汞与土体表面的接触角,在试验中取130°;r为假设孔隙模型的孔隙有效半径。
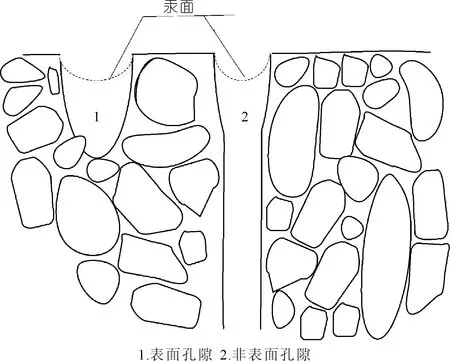
图3 压汞中的2种孔隙Fig.3 Two types of pores in mercury injection
黏土表面往往有着凸凹不平的表面孔隙,这部分孔隙对渗流贡献不大。如图3所示,压汞试验得到的数据是表面孔隙与非表面孔隙两者之和,对此应设法扣除表面孔隙。Dou等[17]认为孔径大于汞的入口压力对应的孔径孔隙是表面孔隙,入口压力可由y轴与压汞曲线在拐点处的切线相交的点确定。因此本文按照此方法排除表面孔隙。
2.2 连通孔隙的方向性
土的渗透性具有方向性[18],压汞试验得到的孔隙率为各个方向的连通孔隙率之和。传统的毛细管模型常常采用如图4所示的极端各向异性简化模型,这样处理会使沿该渗流方向的有效孔隙偏大。因此采用图5所示的考虑3个维度的毛细管模型更能符合实际渗流情况[19]。
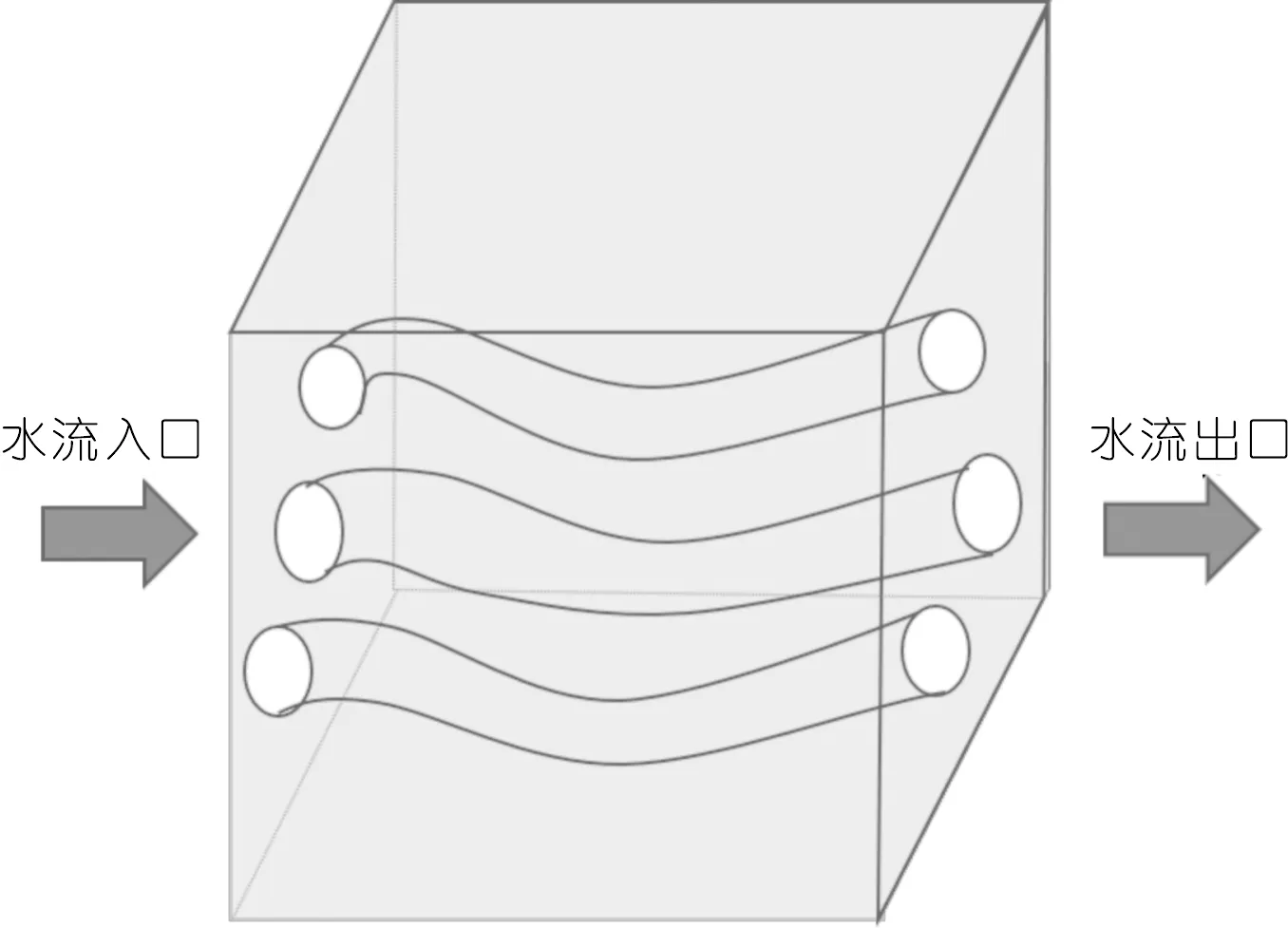
图4 极端各向异性毛细管模型Fig.4 Extremely anisotropic capillary model
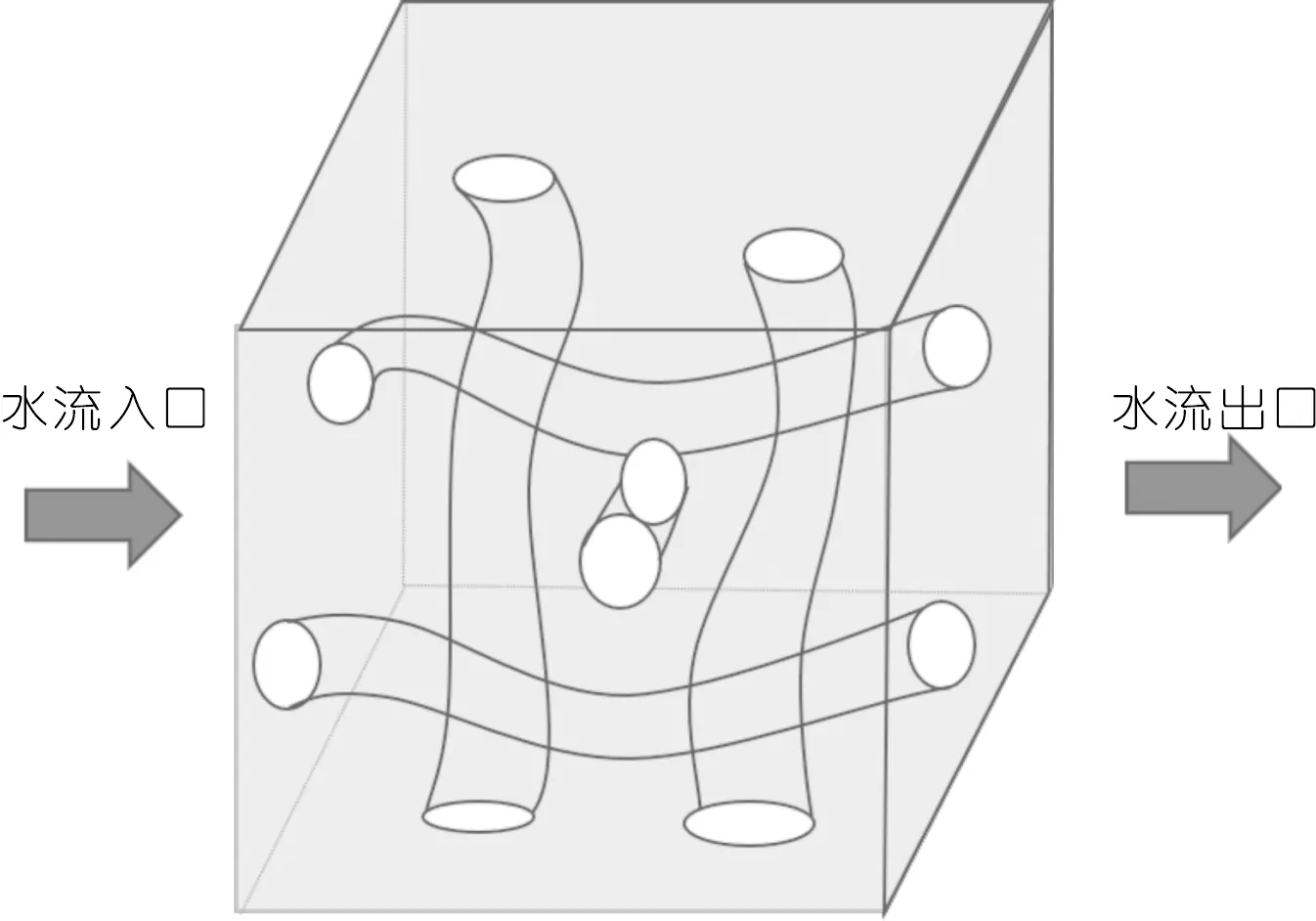
图5 改进后的毛细管模型Fig.5 Modified anisotropic capillary model
利用改进的毛细管模型计算某个方向的渗透系数时,根据有效孔隙定义,只有沿渗流方向的毛细管才视为对该方向渗流有贡献的孔隙。进一步假设孔隙分布与该方向渗流面积有关,因此可以根据各个方向渗流面积计算出渗流方向的有效孔隙率。因此考虑孔隙分布的方向性后,修正的有效孔隙率可表示为
(6)
nc=Ccn
(7)
式中:Cc为渗流方向孔隙率系数,对于立方体试样,3个方向的渗流面积相同,Cc为1/3,n为连通孔隙率,nc为有效孔隙率。
2.3 结合水层
黏土薄片一般带负电,其周围会形成电场,在静电作用下会吸引偶极子以及阳离子等附着在黏土颗粒表面。如图6所示,由于黏土颗粒与水之间静电作用,会导致颗粒表面附着黏滞性很强的结合水层,又称双电层,双电层在微米级到纳米级的孔隙中影响很大。由于双电层内水的流动性可以忽略不计,对渗流贡献很小,因此本文将其视为无效孔隙部分。

图6 考虑结合水层的毛细管模型Fig.6 Capillary model considering the bound water layer
在渗流过程中,可以认为电荷密度的分布满足波尔兹曼(Boltzmann)公式,再结合古依-查普曼(Guoy-Chapman)公式,即可得到双电层厚度公式[8]:
(8)
式中:a表示颗粒表面的双电层厚度,一般为几纳米到几十纳米;λ表示渗滤液介电常数;k为玻尔兹曼常数;T为热力学温度,又称绝对温度;n0为零点电位时的离子浓度。E0为电荷的静电单位,为常数;v为渗流液体中电荷离子价。
基于毛细管模型,可以得到考虑双电层效应后的有效孔隙nu:
(9)
式中:V(r)为孔径为r的孔隙体积,V为试样体积,计算参数均可通过压汞试验获得。
2.4 修正的渗流公式
黏土的孔隙通道大多是蜿蜒曲折的,因此引入曲折因子T来表示黏土孔隙的迂曲程度。定义曲折因子为土中孔隙两端的实际距离与孔隙两端的直线距离之比。准确得出曲折因子的值是一件很困难的事情,不同材料的孔隙曲折情况各不相同,于是大量曲折因子的经验公式被学者提出[20]。本文采用常见的压汞试验确定曲折因子[21]:
T=2.23-1.13Vsd
(10)
式中:Vs为单位质量样品的总孔隙体积,cm3/g,可以通过压汞试验测定;d为样品密度,g/cm3。
综合考虑无效孔隙以及有效孔隙分布特征,结合式(4)可以得到黏土渗流系数公式:
(11)
可以看出式(11)考虑了黏土矿物成分和孔隙的结构性的影响,即孔隙大小分布、曲折度、孔隙方向、双电层等。若考虑无效孔隙为零以及孔隙为沿着渗流方向的均匀笔直毛细管,式(11)则退化为式(4)。
3 算例验证
变水头渗流试验是测定黏土渗透系数的有效方法,土体的渗透系数可由一段时间内变水头管内水头高度的变化求得,具体可以根据式(12)、(13)[20-21]计算:
(12)
(13)
为了进一步验证改进的渗流系数公式可以合适地描述土体结构性,对原状土与重塑土试样进行一系列固结试验以改变孔隙结构。本文分别选取广州市南沙区原状土及重塑土进行变水头渗流试验,采用真空饱和方法进行试样饱和,然后使用南55型渗透仪进行变水头试验,测定水头变化高度与时间,重复3次,取其平均值作为渗透系数,并且要求每次的渗透系数与平均值之差小于±2×10-ncm/s,其中10-n为平均值的量级。对试验完后的原状土及重塑土进行压汞试验,获得土体基本参数如表1所列。
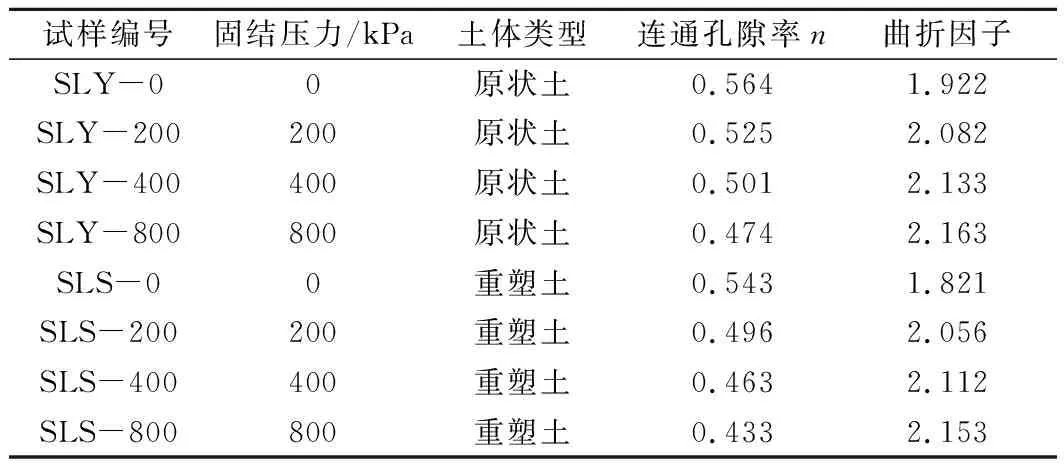
表1 土的基本参数
广州市南沙区原状土及重塑土的孔隙分布特征曲线如图7~8所示。从图7、8中可以看到:随着固结压力的变大,孔径-进汞增量曲线与坐标轴所围成的面积在不断减小,即试样的孔隙率在不断减少,土体中孔隙孔径的分布也在发生改变,即体积较大的孔隙在固结过程中最先被挤压并形成较小的孔隙,而体积较小的孔隙也在固结压力较大时被压缩。除此之外也可看出,原状土在各级固结压力下的进汞增量峰值对应的孔径变化远小于重塑土,这说明原状土中的孔隙孔径分布情况受固结压力变化的影响更小。由于原状土是长期地质历史产物,具有更强的结构性,因此重塑土与原状土的微观孔隙结构对各级固结压力的反应存在明显差异,随着固结压力的增加,其差异性逐渐减小。

图7 原状土孔隙分布曲线Fig.7 Pore distribution curves of the undisturbed soil
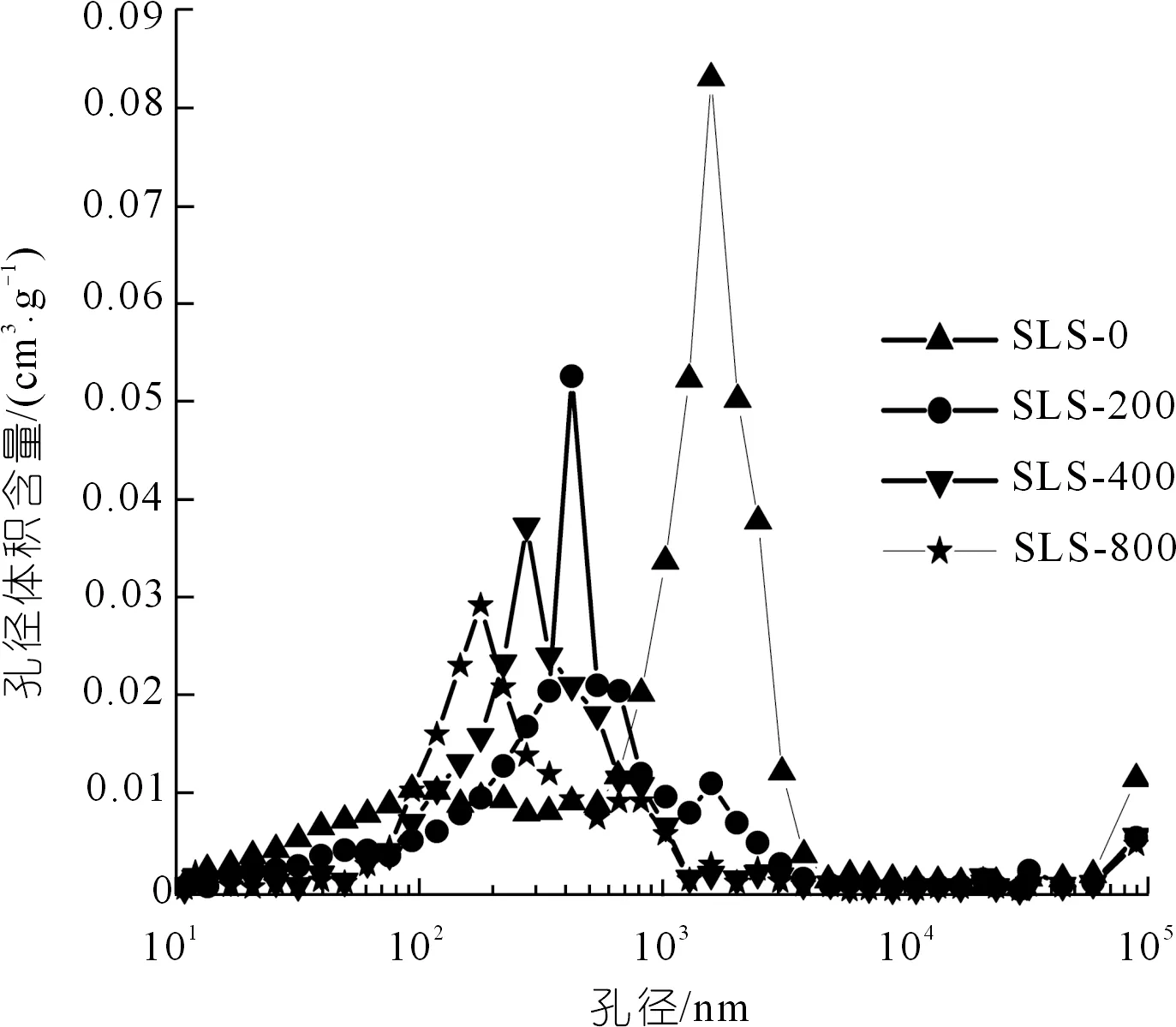
图8 重塑土孔隙分布曲线Fig.8 Pore distribution curves of the remolded soil
从图9~10中可以看出:由于重塑土结构性与长期地质历史的原状土其结构性差别明显,因此其渗透系数、差异性也比较明显,随着固结压力的增长,重塑土与原状土的差别在慢慢减小。对比以上计算结果不难发现:若不考虑有效孔隙和孔隙分布特征,直接将宏观孔隙率代入经验公式,不同固结压力下的广州市南沙区原状土计算结果分别是室内试验测得的11.79,17.01,19.52和22.07倍,而本文公式计算结果则是其1.22,1.81,2.10和2.39倍。重塑土的计算结果是实测值的2.42,8.63,21.89,25.10倍,而本文公式计算结果则是其0.25,0.92,2.36和2.71倍。说明未经修正的斯托克斯孔隙流渗透系数公式并不适用于黏性土。但考虑孔隙的有效孔隙以及其分布特征后,修正后公式的渗透系数计算值与室内试验的实测平均值相比,均在同一量级,相差不大,从而验证了本文黏土渗透系数经验公式的正确性。
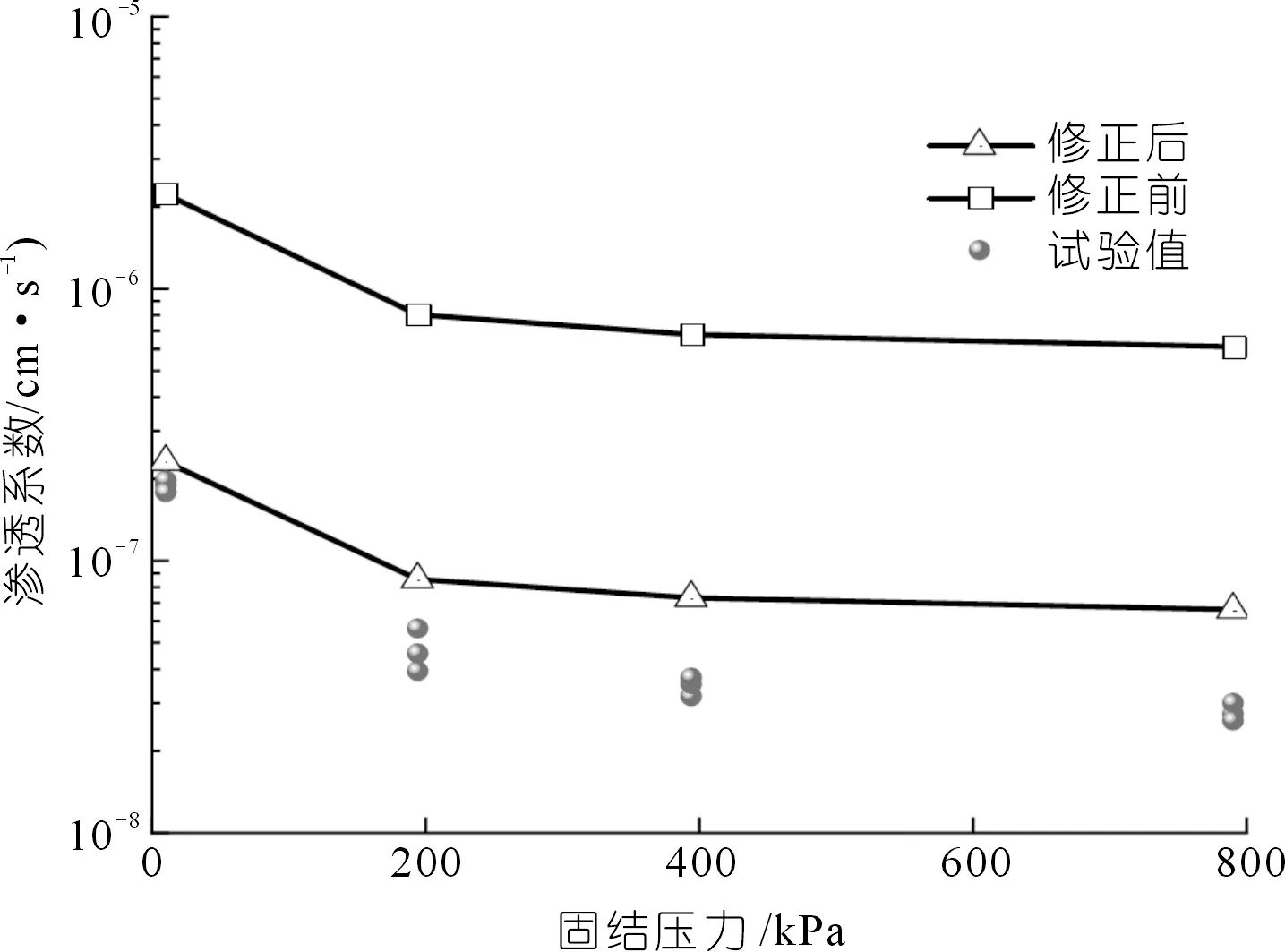
图9 原状土的渗透系数Fig.9 Permeability coefficient of the undisturbed soil

图10 重塑土的渗透系数Fig.10 Permeability coefficient of the remolded soil
4 结 论
(1) 考虑孔隙的有效性以及分布特征,基于哈根-泊肃叶公式可得到改进的黏土渗流公式。若考虑孔隙为零或孔隙为沿着渗流方向均匀的笔直毛细管,本文得出的渗流公式退化为斯托克斯孔隙流渗透系数公式,也可用于粗粒土的渗透系数预测。
(2) 选取不同固结压力下的广州市南沙区原状土及重塑土物理参数,分别利用斯托克斯孔隙流渗透系数公式和提出的修正黏性土经验公式求得渗透系数的计算值,并将其与实测平均值进行对比分析。传统的斯托克斯孔隙流渗透系数公式计算值一般有着10倍以上的偏差,而本文的公式计算值与实测值的偏差一般在4倍以下。
