考虑建筑物荷载的砂性土天然地基附加应力分析

杨 楠，赵 文，柏 谦，路 博

(东北大学 资源与土木工程学院，辽宁 沈阳 110819)

0 引 言

基坑的施工往往伴随着很强的环境效应，基坑开挖必然会引起周围土体应力场的变化，导致周围地基土体变形。基坑开挖变形主要分为3个部分：墙体变形、基坑底部隆起和基坑周围土体的变形。其中墙后土体变形对环境的影响最大，因此本文着重对基坑开挖过程中邻近建筑物下方的土体进行研究。

目前国内外主要采用理论分析和数值模拟两种方法对天然地基的附加应力进行研究，理论分析通常采用Mindlin理论进行计算。Mindlin[1]提出了计算岩土体内任意一点的应力公式，其被广泛用于求解天然地基的附加应力。青二春[2]结合某大型基坑工程，基于Mindlin基本解并考虑残余应力，提出了基坑开挖引起的附加应力，以分层总和法求得坑内土体的回弹模量，确定了开挖卸载作用下纵向沉降曲线模式。童星等[3]基于均布荷载下Mindlin应力解，考虑了分层开挖回弹变形的影响，提出了深大基坑的底部土体卸荷附加应力的计算方法，结合Matlab编程验证了理论的可行性。Chen等[4]结合上海市东方公路地下通道工程，采用Mindlin理论推导出基坑开挖引起的隧道衬砌附加应力，然后在此基础上根据弹性地基梁理论推导出了基坑下方隧道变形的计算公式。Zhang等[5]对既有隧道邻近的深基坑开挖进行研究，在现有Mindlin理论基础上提出了一种半解析方法来预测土体位移以及邻近隧道变形，与工程实测值相比较，吻合较好。魏纲等[6]考虑了基坑坑底与基坑侧壁的卸荷应力以及基坑围护结构的影响，建立了基坑开挖力学计算模型，并基于Mindlin理论解公式，得出了基坑开挖引起的邻近既有地铁隧道的附加荷载计算公式。闫旭丽等[7]采用Mindlin理论计算了基坑底部和基坑侧壁开挖后任意一点的附加应力，应用Matlab求解了邻域隧道的应力场，以此得到了邻近隧道地基土体应力路径的变化规律。刘建文等[8]认为基坑开挖对邻近隧道土体剪切参数的影响较大，将基坑邻近隧道简化成Timoshenko梁，采用Mindlin理论计算了基坑的卸荷作用，建立了基坑开挖使下方盾构隧道产生变形的理论公式。沈国政等[9]通过Mindlin理论计算了深基坑开挖卸荷后引起隧道轴线方向的纵向附加应力，适用于土质较好的情况，并基于差分法求解了开挖基坑导致邻近地铁隧道发生的纵向位移，与监测数据吻合。应宏伟等[10]引入了修正的基床反力系数，将基坑邻近隧道简化为Euler-Bernoulli 梁，建立了以Mindlin解为基础求解基坑开挖卸载时邻近隧道附加应力的简化计算方法，该方法可以考虑埋深因素与地基剪切效应，更接近实际工程。

Beyabanaki等[11]采用三维有限元模拟研究了既有矿井上方的基坑开挖，计算了侧压力系数、矿井尺寸与基坑交叉角度和开挖工序等，以此分析基坑开挖对既有矿井主体结构的附加荷载。周杰等[12]基于Mindlin解，采用Mathmatic软件计算了矩形、不规则形状基坑开挖作用下地铁车站轴线上的附加应力，分析了基坑夹角、深度、隧道走向对隧道附加应力场的影响规律。Hashash等[13]基于深基坑开挖得到的现场数据通过数值计算进行反分析，得到了求解基坑开挖反馈的基因算法和人工神经网络算法，并通过相关基坑工程，验证了正确性。施有志等[14]采用数值模拟考虑基坑-天然地基-基础-建筑物共同作用，计算了地铁基坑开挖引起邻近建筑物产生的变形。楼春晖等[15]对软土基坑从垂直和平行于维护结构两个方向进行监测，总结了基坑开挖对周边建筑物变形的影响。赵斌[16]对多种支护下的深基坑采用监测和模拟两个方法分析了深基坑开挖对近接建筑物群稳定性的影响。

在基坑开挖对周围环境的影响的研究中，大多数学者为简化计算仅考虑基坑四周侧壁和基坑坑底引起的天然地基附加应力，对天然地基上部的建筑物荷载引起的附加应力以及不同工况下的天然地基附加应力影响因素研究较少。因此，将建筑物荷载与基坑四周侧壁及基坑坑底相结合进而求解附加应力的理论方法有待研究，随建筑物荷载的增加，天然地基附加应力的分布规律也需进一步探索。

鉴于此，本文将基坑前、后、左、右四个侧壁以及基坑坑底和建筑物底部所引起的附加应力叠加，得到总的土体附加应力，研究不同附加建筑物荷载和不同基坑开挖距离条件下天然地基的附加应力分布情况。

1 基坑开挖力学模型及假定

基坑开挖的力学模型如图1所示。

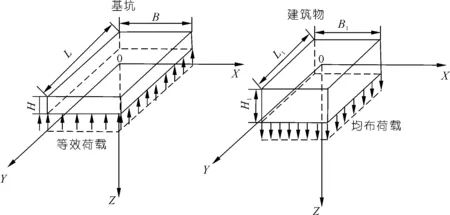
图1 基坑开挖力学模型示意Fig.1 Foundation pit excavation mechanics model diagram

有一开挖深度为H、长度为L、宽度为B的矩形基坑，其右侧有一个埋深为H1、长度为L1、宽度为B1的建筑物。建立三维坐标系，其以地表面(z=0)处基坑矩形荷载范围中心为原点，计算基坑前后左右4个侧壁、基坑坑底所引起的土体附加应力，另建立以地表面(z=0)处建筑物矩形荷载范围中心为原点的坐标系，其用于计算建筑物荷载所引起的附加应力。

本文计算假定：

(1) 土体为均质的半无限弹性空间体；

(2) 不考虑基坑开挖的时间因素和空间因素，不考虑降水；

(3) 坑底荷载为均布荷载，大小为开挖掉的土体自重应力γH(γ为土体重度)，方向向上；

(4) 基坑四周侧壁在开挖后会产生应力释放，等效为在侧壁施加向坑内的三角形水平向分布荷载K0γc，其中，K0为静置土压力系数，砂性土时，K0=1-sinθ，c为作用力埋深；

(5) 不考虑基坑围护结构、土体加固等因素对卸荷附加应力计算的影响；

(6) 不考虑建筑物侧壁引起的附加应力，只考虑建筑物底部引起的土体附加应力。

2 天然地基附加应力理论解

目前土体应力的计算方法通常采用弹性理论公式，把地基土视为连续的、均匀的、各向同性的半无限空间体，这种假定与土体的实际情况有差别，但是计算结果能满足工程实际的要求[17]。1936年，Mindlin[1]基于Galerkin位移函数推导出了在半无限空间体内部作用一集中力时空间体内部任意一点的应力公式，适用于分析岩土工程中涉及到的附加应力问题。

图2和图3分别是水平力及竖向力作用下Mindlin解示意图。

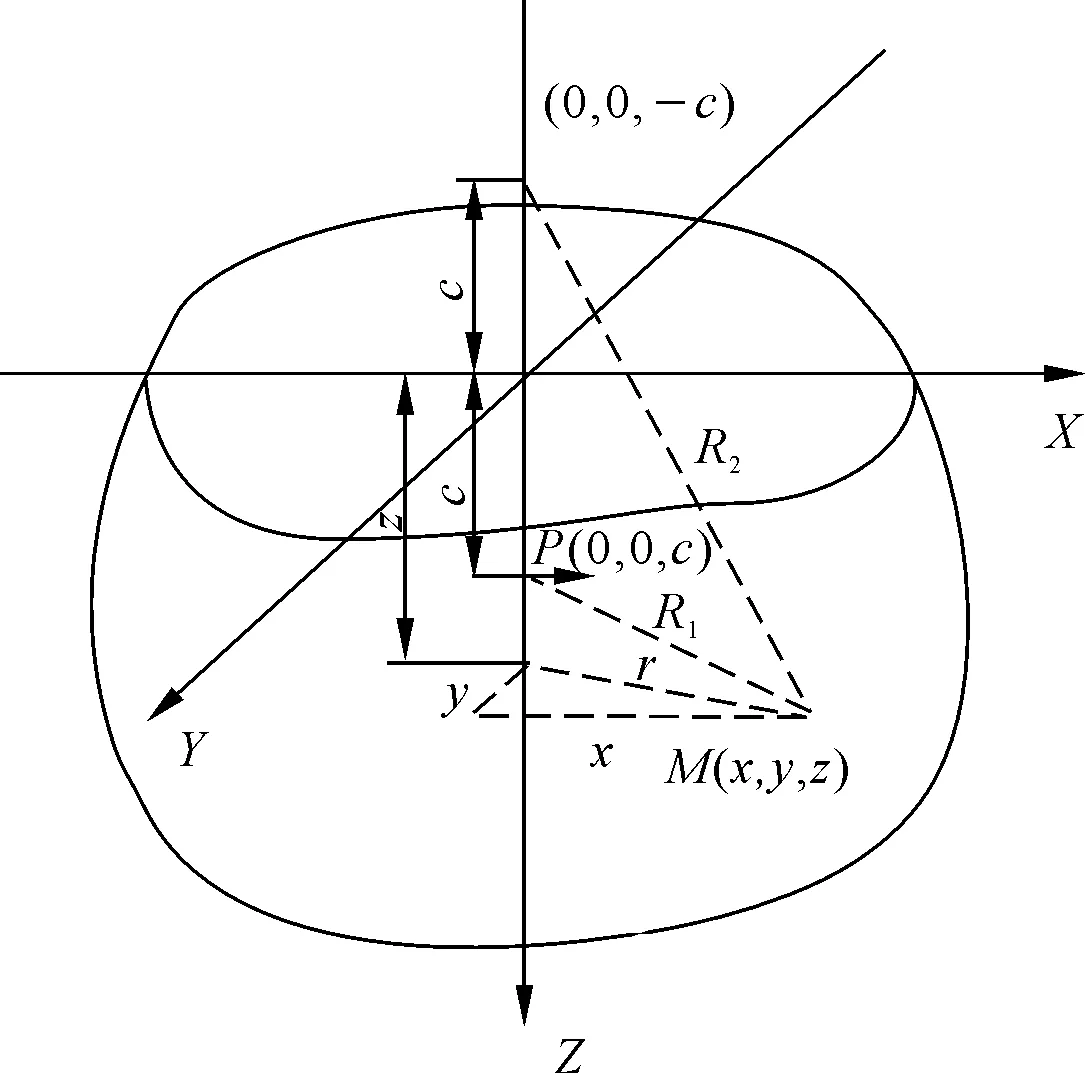
图2 水平力作用下Mindlin解示意Fig.2 Schematic of Mindlin solution under horizontal force

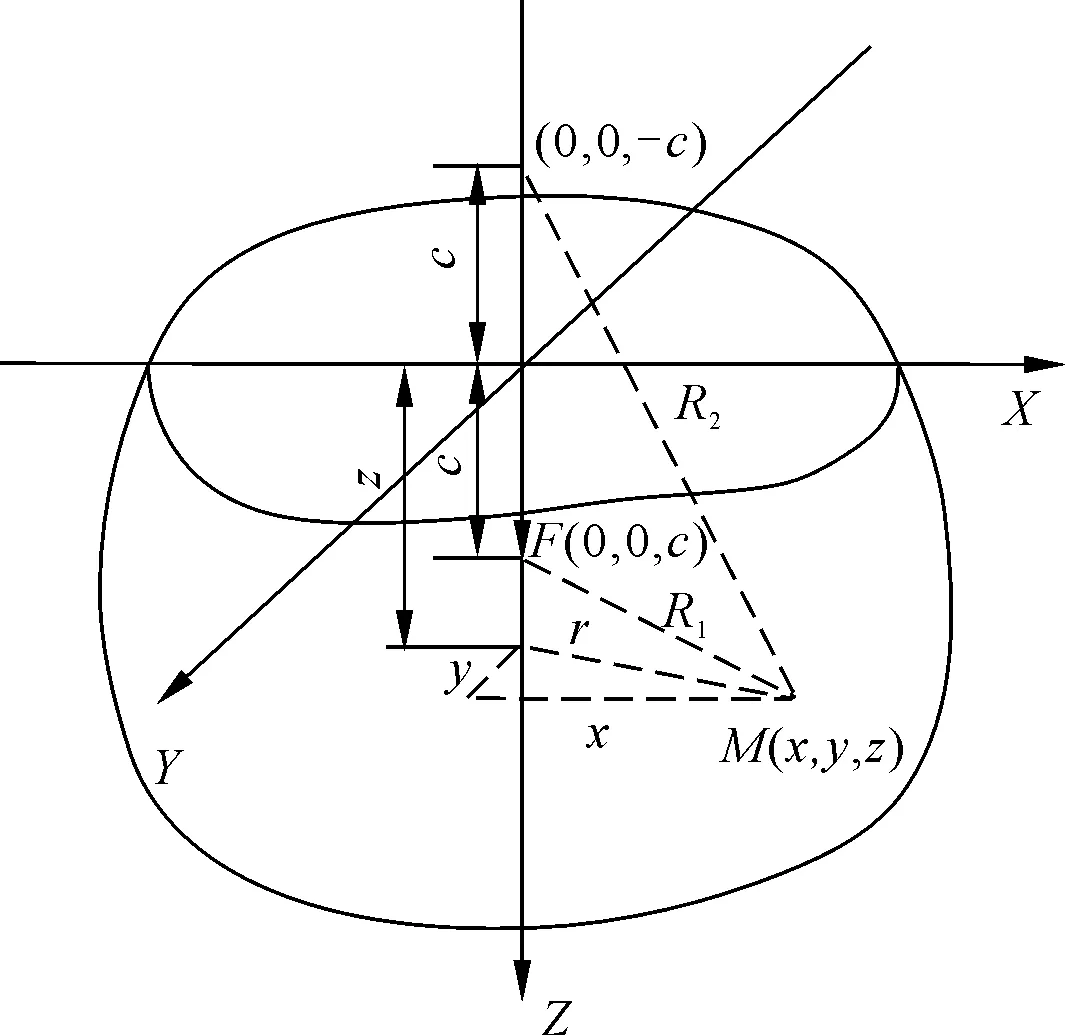
图3 竖向力作用下Mindlin解示意Fig.3 Schematic of Mindlin solution under vertical force

如图2所示，在地表以下c深度位置作用一处水平集中力P，推导出土体中任一点(x，y，z)处的附加应力为

(1)

(2)

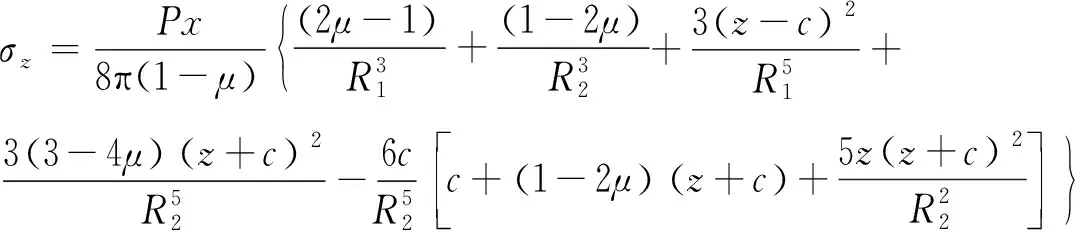
(3)

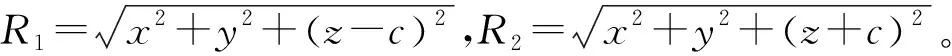
如图3所示，在地表以下c深度位置作用一竖向集中力F，推导出土体中任一点(x，y，z)处的附加应力为

(4)

(5)

(6)

上述各公式中：x为所求点距离力作用点的水平距离，m；y为所求点距离力作用点的横向距离，m；z为所求点埋深，m；P为水平集中力，kN；F为竖向集中力，kN；c为集中力作用点的埋深，m；μ为土体的泊松比。

通过公式可以看出，研究区域与集中力作用点的距离和集中荷载对附加应力影响较大，因此本文重点研究附加荷载及基坑开挖距离变化对天然地基附加应力的影响。设基坑左侧壁、右侧壁、前侧壁、后侧壁、坑底和建筑物底部等位置所引起的正向、侧向、竖向附加应力分别为σx1～σx6、σy1～σy6、σz1～σz6。

限于篇幅，本文只列出基坑左侧壁、前侧壁、坑底和建筑物荷载引起的附加应力。

2.1 基坑左侧壁卸荷分析

基坑左侧壁三角形分布荷载坐标为(-B/2，η，c)，B是基坑宽度，η和c分别表示基坑左侧壁上作用力的纵坐标和竖坐标，单位均为m。由Mindlin水平荷载的基本应力解，得出单位力K0γcdηdc引起建筑物下方某一点(x0，y0，z0)的附加应力如下：

(7)

(8)

(9)

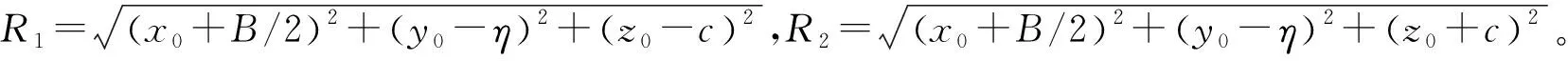
2.2 基坑前侧壁卸荷分析

基坑前侧壁三角形分布荷载坐标为(ξ，L/2，c)，L是基坑长度，ξ和c分别表示基坑前侧壁上作用力的横坐标和竖坐标，单位均为m。由Mindlin水平荷载的基本应力解，得出单位力K0γcdξdc引起建筑物下方某一点(x0，y0，z0)的附加应力如下：

(10)

(11)

(12)

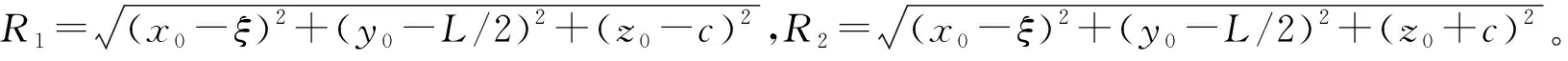
2.3 基坑坑底卸荷分析

基坑坑底等效荷载坐标为(ξ，η，H)，H是基坑开挖深度，ξ和η分别表示基坑坑底上作用力的横坐标和纵坐标，单位均为m。由Mindlin竖向荷载的基本应力解，得出单位力γHdξdη引起建筑物下方某一点(x0，y0，z0)的附加应力如下：

(13)

(14)

(15)

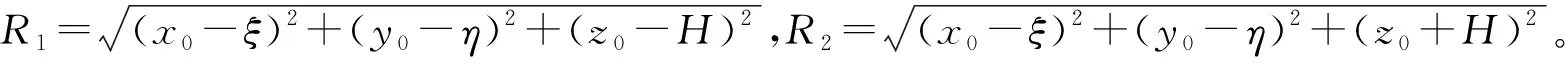
2.4 建筑物荷载引起附加应力分析

建筑物底部均布荷载坐标为(ξ，η，H1)，H1是建筑物埋深，ξ和η分别表示建筑物底部作用力的横坐标和纵坐标，单位均为m。由Mindlin竖向荷载的基本应力解，得出单位力Q0dξdη引起建筑物下方某一点(x0，y0，z0)的附加应力如下，Q0为均布荷载，单位为kPa：

(16)

(17)

(18)

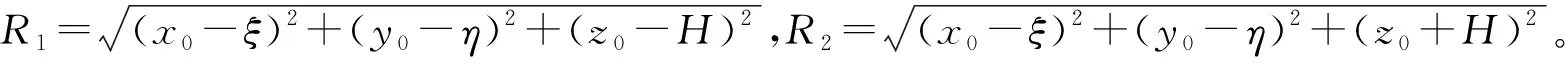
将在基坑4个侧壁、基坑坑底和建筑物底部的共同作用下引起土体中任一点(x0，y0，z0)处产生的附加应力叠加，得到基坑开挖引起的周围土体总的附加应力计算公式为

(19)

上述公式中积分计算过程比较复杂，本文利用Matlab数值积分进行循环计算。为了进一步验证本文提出理论解的正确性与合理性，将本文得到的基坑开挖引起的附加应力计算公式与魏纲等[6]人提出的计算方法在相同工况下进行对比，对比结果如图4所示。由图可知本文计算结果与魏纲等人的计算结果基本吻合。

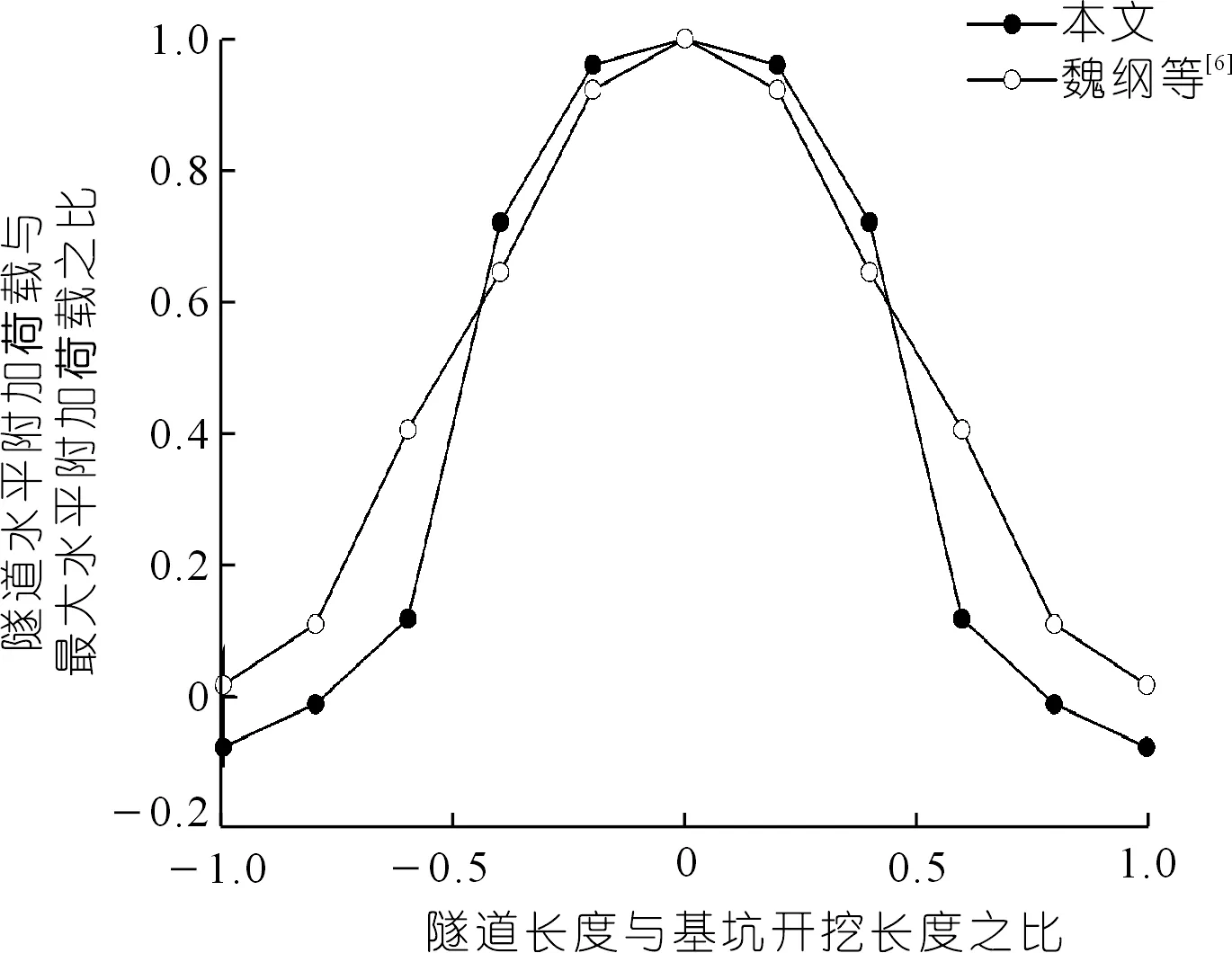
图4 隧道水平附加荷载量纲对比分析Fig.4 Comparative analysis on horizontal surcharge loads in tunnel

建筑物荷载和基坑开挖共同作用下的附加应力，在实际情况中难以实测，所以与本文工况相近的现场试验数据和理论计算结果几乎没有。为此建立有限元模型，用数值方法对建筑物荷载及前文提出的总附加应力公式进行验证，有限元计算模型如图5所示。

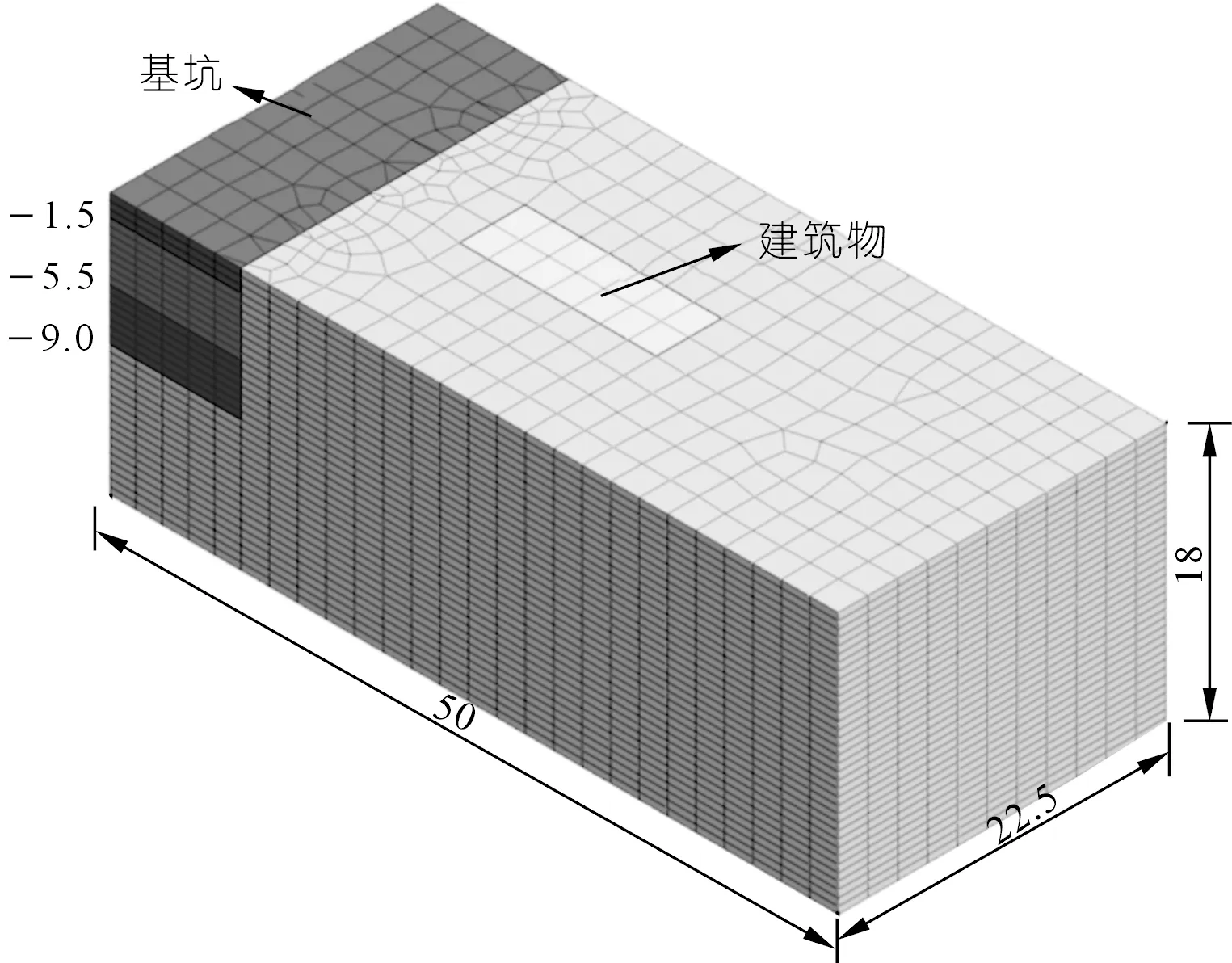
图5 计算模型(尺寸单位：m)Fig.5 Numerical calculation model diagram

建筑物附加荷载为700 kPa，基坑开挖距离为6 m。土体采用修正摩尔库伦本构，实体单元建模，建筑物采用弹性本构，实体单元建模。其余计算参数均与文中保持一致，提取建筑物正下方中心点处的正向附加应力结果进行对比，结果如图6所示。

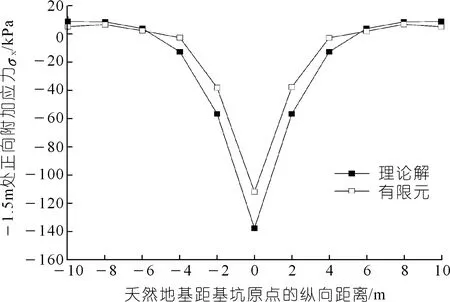
图6 正向应力对比结果Fig.6 Comparison of normal additional stress

由图6可知，采用本文提出的理论公式得到的正向附加应力整体变化规律与有限元相似，理论计算结果大于有限元计算结果，说明理论计算公式比较保守。理论解的最大值比有限元最大值大18.83%，由于理论解为弹性解，而有限元为弹塑性计算，所以会有一定的误差，但误差在20%以内，说明本文计算公式具有一定的准确性。

3 天然地基附加应力影响因素分析

本文基于Mindlin解公式研究不同附加荷载、不同基坑开挖距离条件下，基坑开挖引起邻近建筑物下方天然地基的附加应力。图7为主要研究位置分布图。

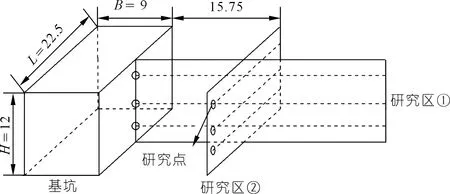
图7 研究点位置(尺寸单位：m)Fig.7 Location of study sites

本文主要研究范围为交叉垂直布置的两个矩形区域，垂直基坑长边区域为研究区①，平行基坑长边区域为研究区②。每个区域布置三排点，每排点的深度与基坑开挖分步深度相同。图7中两个矩形区域中同一深度位置相邻两两研究点的间距均为2 m，研究区②与基坑轴线的水平距离为15.75 m。第一步开挖1.5 m，第二步开挖4.0 m，第三步开挖3.5 m。静止土压力系数K0取值0.41，土体重度γ为15.47 kN/m3，泊松比μ为0.3，内摩擦角为35.5°。

3.1 附加荷载引起的附加应力分析

为研究在不同附加荷载条件下，基坑开挖引起的天然地基附加应力规律，本节基坑开挖距离取为9 m，附加荷载分别取200，300，500，700，1 000，1 500 kPa，在基坑开挖引起的附加应力基础上计算。

图8为研究区①在-1.5 m埋深处不同附加荷载引起的天然地基正向、侧向和竖向附加应力图。

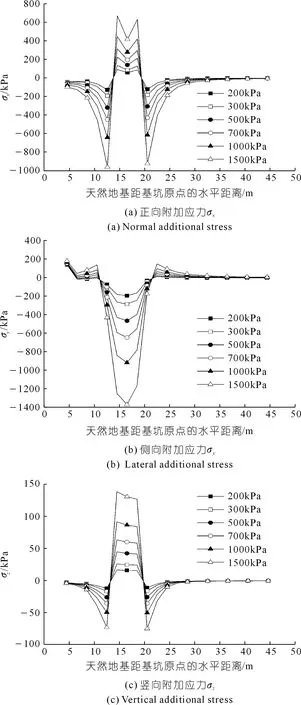
图8 研究区①-1.5 m处的正向、侧向、竖向附加应力Fig.8 Normal，lateral and vertical additional stress calculation results at -1.5 m of research area 1

由图8(a)可知，在不同附加荷载作用下，天然地基的正向应力变化规律基本相同。在基坑右侧壁与建筑物左侧壁之间的范围内，土体主要承受压应力，随着距基坑原点距离的增加，正向应力逐渐增大，在距基坑原点12.5 m处(紧挨建筑物左侧壁)出现最大正向应力；在建筑物左侧壁与建筑物中心点之间，土体主要承受拉应力，在距基坑原点14.5 m处(建筑物内部靠近左侧壁)出现最大拉应力；在建筑物中心以后土体主要承受压应力，随着与基坑原点距离的增加，正向应力逐渐减小，最后趋近于零。

由图8(b)可知，在基坑右侧壁与建筑物左侧壁之间的范围内，土体主要承受的侧向应力为拉应力，随着与基坑原点距离的增加，侧向应力先减小后增大，在距基坑原点4.5 m(即基坑右侧壁处)处出现最大侧向拉应力；在建筑物左侧壁与建筑物中心点之间，土体主要承受压应力，呈现先增大后减小的趋势，在距基坑原点16.5 m处出现最大压应力；在建筑物中心以后土体主要承受拉应力，随着与基坑原点距离的增加，侧向应力逐渐减小，最后趋近于零。

由图8(c)可知，研究区①在-1.5 m埋深处的竖向应力与正向应力变化趋势相同。表1是不同附加荷载引起的研究区②在-1.5 m处的总的正向应力。

图9为研究区②在-1.5 m埋深处不同附加荷载引起的天然地基正向、侧向和竖向附加应力图。可以发现，三种应力分布都是关于x=0轴线对称。

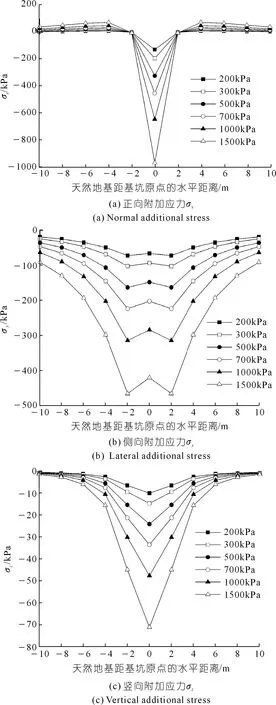
图9 研究区②-1.5 m处的正向、侧向、竖向附加应力Fig.9 Normal，lateral and vertical additional stress calculation results at -1.5 m of research area 2

由图9(a)可知，研究区②边界到建筑物前侧壁的范围内主要承受的正向应力为拉应力，且与建筑物越近正向应力越大，但是总体变化趋势不大，在建筑物正下方出现最大压应力。

由图9(b)可知，天然地基主要承受的侧向应力为压应力，与建筑物越近侧向应力呈先增大后减小的趋势，最大侧向应力出现在建筑物前侧壁附近。

由图9(c)可知，研究区②的竖向应力为压应力，与建筑物越接近竖向应力越大，在建筑物正下方出现最大压应力。

天然地基研究区①和研究区②在-1.5 m深度处三种应力随不同附加荷载的增长比例结果见表1。

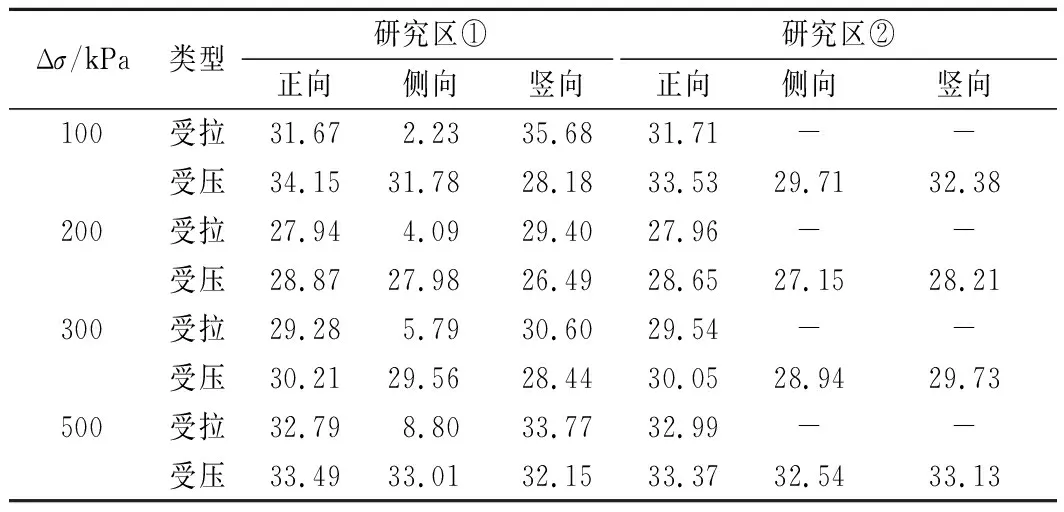
表1 天然地基-1.5 m处附加应力增长比例

由表1可知：在-1.5 m深度处，当附加荷载每增加100，200，300，500 kPa时，研究区①最大拉应力增幅为竖向应力，分别达35.68%，29.40%，30.60%，33.77%，最小拉应力增幅出现在侧向应力，分别为2.23%，4.09%，5.79%，8.80%；最大压应力增幅出现在正向应力，分别为34.15%，28.87%，30.21%，33.49%，最小压应力增幅出现在竖向应力，分别为28.18%，26.49%，28.44%，32.15%。

研究区②中最大压应力增幅出现在正向应力，为33.53%，28.65%，30.05%，33.37%；最小压应力增幅出现在侧向应力，为29.71%，27.15%，28.94%，32.54%。

图10为研究区①在-5.5 m埋深处不同附加荷载引起的天然地基正向、侧向和竖向附加应力图。

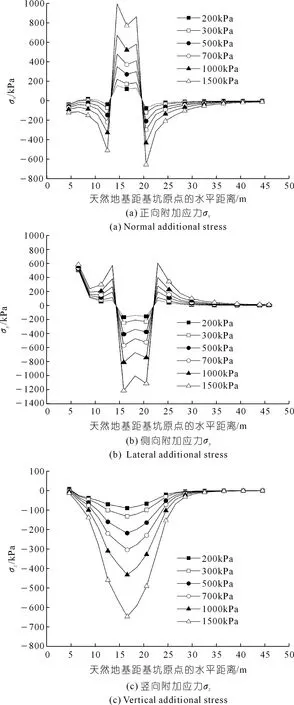
图10 研究区①-5.5 m处正向、侧向、竖向附加应力Fig.10 Normal，lateral and vertical additional stress calculation results at -5.5 m of research area 1

由图10(a)可知，研究区①在-5.5 m深度的正向应力变化趋势与在-1.5 m的变化趋势相同，最大压应力出现在建筑物中心右侧附近。由图10(b)可知，研究区①在-5.5 m深度的侧向应力整体变化趋势与在-1.5 m的变化趋势相同，但最大压应力出现在建筑物左侧壁内侧，最大拉应力出现在建筑物中心点右侧。由图10(c)可知，研究区①在-5.5 m处的竖向应力为压应力，在16.5 m处(建筑物左侧壁与建筑物中点之间)出现最大压应力。

图11为研究区②在-5.5 m埋深处不同附加荷载引起的天然地基正向、侧向和竖向附加应力图。

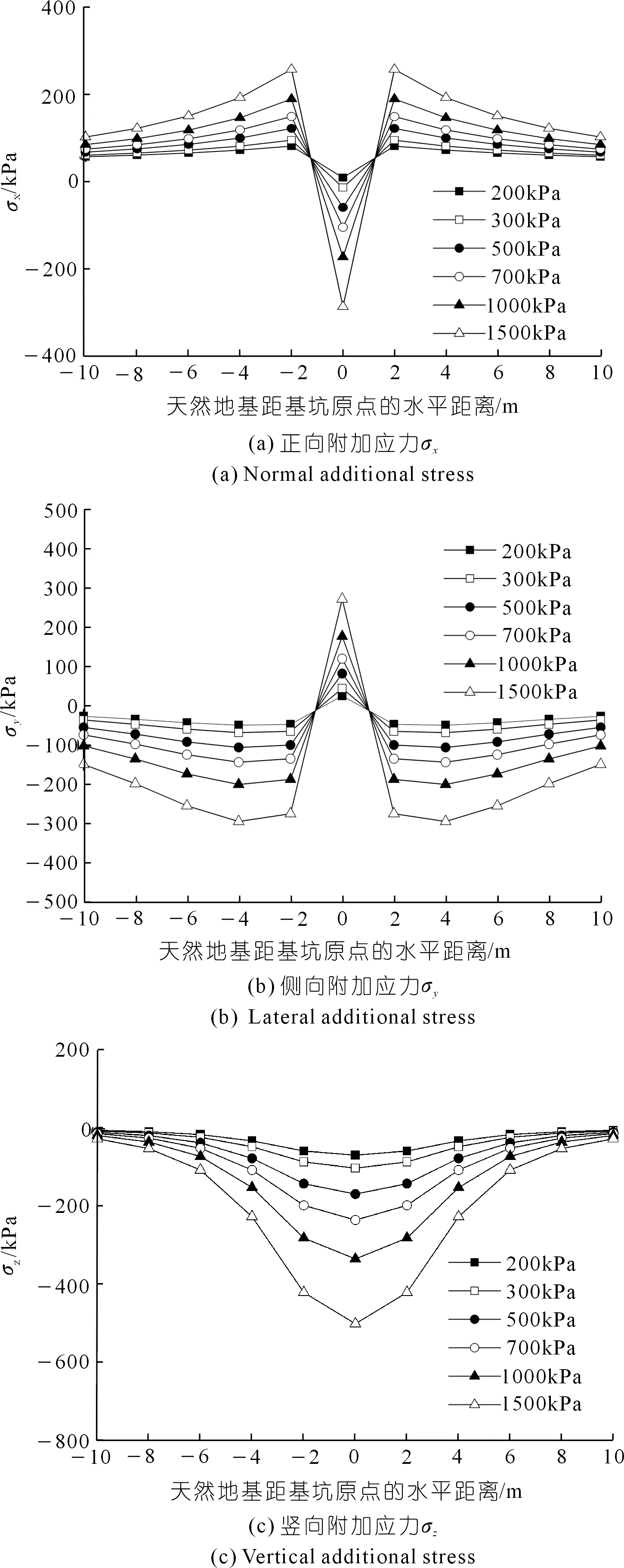
图11 研究区②-5.5 m处正向、侧向、竖向附加应力Fig.11 Normal，lateral and vertical additional stress calculation results at -5.5 m of research area 2

由图11(a)和图11(c)可知，研究区②在-5.5 m处正向应力和竖向应力的变化趋势与在-1.5 m处相同。由图11(b)可知，研究区②在边界(y=-10)与建筑物前侧壁(y=-2.25)范围内主要承受的侧向应力为压应力，与建筑物越近竖向应力呈现先增大后减小趋势，最大压应力出现在y=-4 m处。在建筑物正下方范围内主要承受的竖向应力为拉应力，最大拉应力出现在建筑物中心位置。

类似于表1，列出天然地基研究区①和研究区②在-5.5 m深度处三种应力随不同附加荷载的增加比例(表格略)。经分析，在-5.5 m深度处，当附加荷载增加100，200，300，500 kPa时，研究区①最大拉应力增幅出现在侧向应力，分别达35.87%，29.46%，30.63%，33.81%；最大压应力增幅出现在正向应力，分别达37.88%，30.13%，31.12%，34.14%，最小压应力增幅出现在竖向应力，分别达32.2%，28.15%，29.53%，33.13%。研究区②中最大拉应力增幅出现在侧向应力，分别为40.9%，31.06%，31.76%，34.77%；最大压应力增幅出现在正向应力中，为38.7%，30.38%，31.32%，34.29%；最小压应力增幅出现在侧向应力中，为28.48%，26.66%，28.54%，32.24%。

研究区①和研究区②在-9 m处天然地基的附加应力变化趋势与在-5.5 m处的附加应力变化趋势基本相同：当附加荷载每增加100，200，300，500 kPa时，研究区①最大拉应力增幅出现在侧向应力，分别为35.24%，29.62%，30.44%，33.9%；最大压应力增幅出现在正向应力，分别为41.34%，31.02%，31.67%，34.69%；最小压应力增幅出现在竖向应力，分别为30.26%，27.90%，29.21%，32.87%。研究区②中最大拉应力增幅出现在侧向应力，分别为40.00%，30.98%，31.40%，34.49%；最大压应力增幅出现在正向应力，为47.82%，32.57%，32.99%，35.40%；最小压应力增幅出现在侧向应力，为27.77%，26.54%，28.02%，32.03%。

分析在不同附加荷载条件下，-1.5，-5.5，-9.0 m深度处的天然地基附加应力可知，与200 kPa附加荷载时的天然地基附加应力相比，附加荷载每增加100，200，300 kPa和500 kPa，天然地基附加应力分别增加了36.0%，46.6%，60.8%和81.2%。由此可见，天然地基附加应力的增长比例与附加荷载的增量呈线性关系，将数据拟合得到如下关系式：

Y=0.1142x+24.737

(20)

式中：x为附加荷载的增量，kPa；Y为附加应力增长百分比，%。

该公式适用于砂性土天然地基情况下，求基坑开挖引起的建筑物下方最大附加应力。

3.2 不同开挖距离引起的附加应力分析

为研究在不同基坑开挖距离条件下，基坑开挖引起的天然地基附加应力规律，本文附加荷载取700 kPa，基坑开挖距离分别取2，3，6，9，12，15 m进行分析计算。图12为研究区①在-1.5 m埋深处，不同基坑开挖距离引起的天然地基正向、侧向和竖向附加应力图。

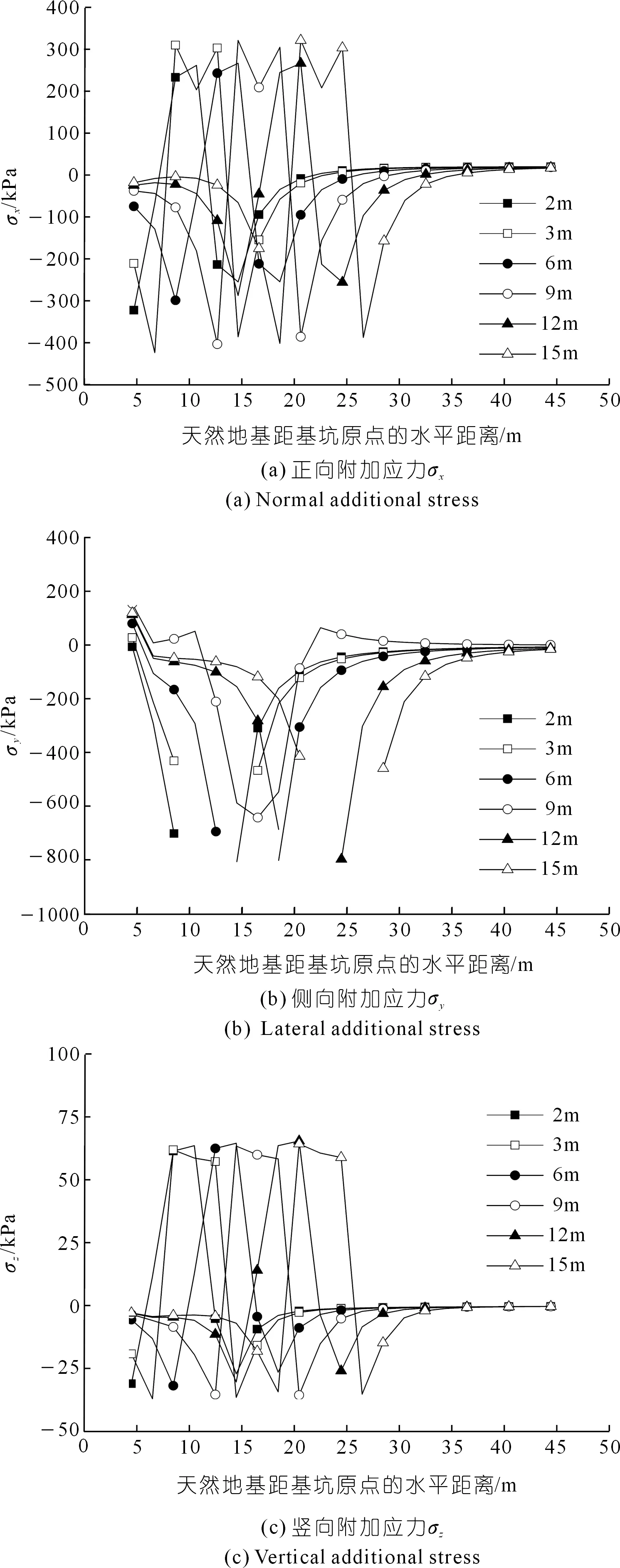
图12 不同开挖距离下研究区①-1.5 m处正向、侧向、竖向附加应力Fig.12 Normal，lateral and vertical additional stress calculation results at -1.5 m of research area 1 under different excavation distances

由图12(a)可知，在不同的基坑开挖距离条件下，天然地基在基坑右侧壁(x=4.5 m)与建筑物左侧壁均主要承受压应力。在开挖距离为2 m时，最大压应力出现在基坑右侧壁处；在开挖距离为3，6，9 m时，压应力逐渐增大，在开挖距离为12，15 m时，压应力先减小后增大，最大压应力均出现在建筑物左侧壁附近。在建筑物左侧壁与建筑物中心范围内主要承受拉应力，拉应力在250～320 kPa范围内；在建筑物中心之后主要承受压应力，随着与基坑原点距离的增加，压应力逐渐减小最后趋近于零。

在计算-1.5 m处侧向附加应力时，由于计算过程中某些计算点因积分域重合出现无限值，因此图12(b)中某些点的应力值出现缺失，但整体看，天然地基主要承受的侧向应力为压应力。

由图12(c)可知，竖向附加应力变化趋势与正向附加应力变化趋势基本相同，最大拉应力值在62～66 kPa之间，最大压应力值在30～36 kPa之间。

图13为研究区②在-1.5 m埋深处，不同基坑开挖距离引起的天然地基正向、侧向和竖向附加应力图。

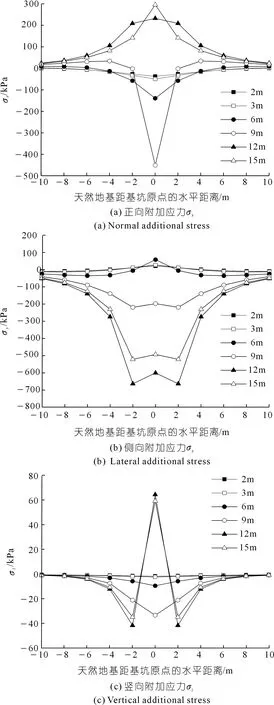
图13 不同开挖距离下研究区②-1.5 m 处正向、侧向、竖向附加应力Fig.13 Normal，lateral and vertical additional stress calculation results at -1.5 m of research area 2 under different excavation distances

由图13(a)可知，基坑开挖距离为2，3，6 m时天然地基承受的正向附加应力主要为压应力，应力变化趋势基本相同。随着与建筑物距离的缩小，压应力逐渐增大，并在建筑物中心处达到最大；在开挖距离为9 m时，在建筑物底面范围之外主要承受拉应力，在建筑物范围内承受压应力；基坑开挖距离为12，15 m时，主要承受拉应力，与建筑物距离越近拉应力越大，在建筑物中心位置拉应力达到最大。

由图13(b)可知，基坑开挖距离为2，3，6 m时，建筑物底面范围内主要承受拉应力，其余位置承受压应力，且压应力随着与建筑物距离的缩小逐渐减小；基坑开挖距离为9，12，15 m时，天然地基主要承受压应力，与建筑物越近侧向应力呈先增大后减小的趋势，最大侧向应力出现在建筑物前侧壁附近。

由图13(c)可知，基坑开挖距离为2，3，6，9 m时天然地基主要承受的竖向应力为压应力，且压应力逐渐增大，在建筑物中心位置达到最大；基坑开挖距离为12，15 m时，建筑物中心位置承受的竖向应力为拉应力，其余位置为压应力。

图14为研究区①在-5.5 m埋深处，不同基坑开挖距离引起的天然地基正向、侧向和竖向附加应力图。

图14 不同开挖距离下研究区①-5.5 m处正向、侧向、竖向附加应力Fig.14 Normal，lateral and vertical additional stress calculation results at -5.5 m of research area 1 under different excavation distances

由图14(a)可知，不同的开挖距离条件下，天然地基正向附加应力变化趋势基本相同，在基坑右侧壁与建筑物左侧壁之间土体主要承受压应力，在建筑物左侧壁至建筑物中心范围内主要承受拉应力，最大拉应力在465～530 kPa范围内；在过建筑物中心以后承受压应力，并且随着距基坑原点距离的增加，压应力逐渐减小最后趋近于零。

由图14(b)可知，侧向应力与正向应力所受应力类型相反，在基坑右侧壁与建筑物左侧壁之间土体的侧向附加应力主要为拉应力，在建筑物左侧壁至建筑物中心范围内主要承受压应力，最大压应力在510～600 kPa；在建筑物中心以后承受拉应力，且随着与基坑原点距离的增加，拉应力逐渐减小最后趋近于零。

由图14(c)可知，不同开挖距离下的竖向附加应力变化趋势相同且最大值与最小值相近，最大压应力均出现在建筑物左侧壁附近，最大压应力值在290～320 kPa范围内。

图15分别为研究区②在-5.5 m埋深处，不同基坑开挖距离引起的天然地基正向、侧向和竖向附加应力图。

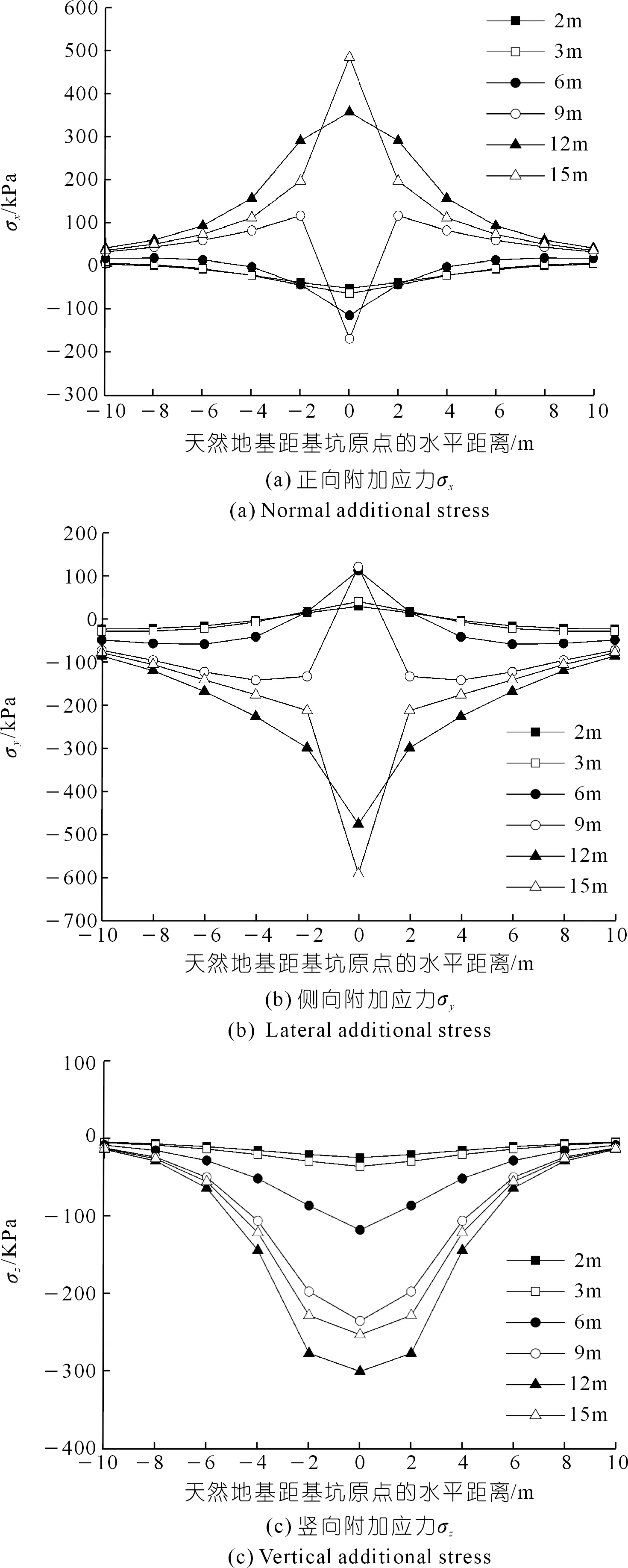
图15 不同开挖距离下研究区②-5.5 m处正向、侧向、竖向附加应力Fig.15 Normal，lateral and vertical additional stress calculation results at -5.5 m of research area 2 under different excavation distances

由图15(a)可知，开挖距离为2，3，6 m时的正向附加应力变化趋势相同，主要承受压应力，随着与建筑物距离的缩小压应力逐渐增大，在建筑物中心位置出现最大压应力。开挖距离为12，15 m时的正向附加应力变化趋势相同，主要承受拉应力，随着与建筑物的距离的缩小拉应力逐渐增大，在建筑物中心位置出现最大拉应力。开挖距离为9 m时，建筑物中心位置处承受压应力，其余位置承受拉应力。

由图15(b)可知，研究区②在-5.5 m时所受侧向附加应力与正向附加应力的变化趋势关于x轴对称，在此不做详细阐述。

由图15(c)可知，天然地基研究区②在-5.5 m处的竖向附加应力主要为压应力，随着距建筑物距离的缩小，压应力逐渐增大，且随着开挖距离的增大，竖向应力最大值也逐渐增大，最大压应力值出现在开挖距离12 m处。

研究区①、研究区②在-9.0 m埋深处，不同基坑开挖距离引起的天然地基正向、侧向和竖向附加应力变化趋势与在-5.5 m处的附加应力变化趋势整体相同，不再赘述。

4 结 论

(1) 天然地基附加应力的增长比例与附加荷载的增量呈线性关系，附加荷载每增加100 kPa，天然地基附加应力增加约36%。

(2) 对于本文中的基坑开挖而言，随着基坑开挖距离的增加，同一深度处天然地基的正向附加应力、侧向附加应力和竖向附加应力的最大值基本处在同一范围内，变化不大，且最大值位置均在建筑物左侧壁附近，埋深越大，附加应力的最值越大。

(3) 对平行基坑长边一侧方向的天然地基，当建筑物中心位于研究区②左侧时，天然地基的正向附加应力和竖向附加应力主要为压应力，侧向应力在建筑物底面范围内主要为拉应力；当建筑物中心位于研究区②的右侧时，天然地基的正向附加应力主要为拉应力，侧向附加应力主要为压应力，竖向附加应力在建筑物中心位置为拉应力，附加应力的最值除研究区②的 -1.5 m 的侧向应力外均出现在y=0处。