电性源瞬变电磁有限差分偏移成像方法
2023-02-11鲁凯亮樊亚楠李貅周建美
鲁凯亮,樊亚楠,李貅*,周建美
1 长安大学地质工程与测绘学院,西安 710054 2 长安大学地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室),西安 710054
0 引言
近二十年来,电性源瞬变电磁法取得了较快的发展与众多成果,目前已在地质调查、地下水监测以及煤层采空区探测等领域取得较好效果(Mogi et al.,1998,2009; Wang et al.,2013; Ito et al.,2014; Di et al.,2018,2020; 底青云等, 2019; Lu et al.,2021).目前为止,电性源瞬变电磁法最常用到的解释方法是(视)电阻率成像,但是(视)电阻率对地质体界面的分辨率较弱,使得对地质结构的解释有待进一步提高.针对这一问题,国内外学者在电磁资料解释方面,引入地震偏移成像理论,实现了瞬变电磁拟地震成像解释技术.
Lee等(1987)利用有限差分法对大地电磁数据向下延拓,并使用偏移成像技术对数据进行解释.魏胜和王家映(1993)基于反射原理,使用偏移成像方法对大地电磁数据进行处理,显著提高了水平方向地层的分辨率,并获得较为丰富的地质界面信息.Strack 和Vozoff(1996)对长偏移距的瞬变电磁数据进行了拟地震成像处理.Gershenson(1997)提出使用虚拟波场的传播特性解释时间域扩散场的电磁信号,以此得到介质的电性分布特征.同年,Zhdanov 和Portniaguine(1997)借鉴地震勘探中的逆时偏移思想,提出了偏移电磁场的概念,并进行了深入研究.随后,吕国印(1998)使用格林函数实现了电磁数据的二维逆时偏移,并对实际资料进行处理,处理后的结果与已知资料吻合较好.陈本池等(1999)将瞬变电磁扩散场信号转化为虚拟波场,直接使用地震领域的偏移成像技术,得到了与理论模型吻合较好的偏移成像结果.进入21世纪后,李貅等(2010)和戚志鹏等(2013)在得到虚拟波场之后,使用柯希霍夫积分法将地面的虚拟波场向下延拓,得到了较好的地质界面信息.此外,樊亚楠等(2019)借鉴地震勘探中的Born近似成像方法,实现了瞬变电磁虚拟波场成像,并对煤层采空区的电磁数据进行处理,对电性界面的识别取得了较好的效果.
在众多的数值计算方法中,有限差分偏移成像技术因其适应性较强的优势在地震勘探领域中起到了巨大的推动作用(马在田,1989).Alford等(1974)对如何提升有限差分法的精度做了详细研究,研究表明只要网格尺寸小于最小波长的1/2,并且离散网格足够精细,则可以得到精确的正演结果.Kelly 等(1976)使用二阶有限差分的声波方程合成了人工地震记录.同一年,Madariaga(1976)成功地模拟了弹性波在介质中的传播规律.Virieux(1986)引入交错网格,模拟了P波和SV波传播过程.在此之后,Levander(1988)对时间项采用二阶差分,空间上采用四阶差分的策略,进一步提高了数值模拟的精度.在此基础上,Crase(1990)将交错网格的有限差分法的精度发展为任意阶,但该方法需要的计算量和内存都比较大.Graves(1996)在二维有限差分法的基础上进一步研究,提出了三维地震的有限差分仿真技术,并研究了地震波在三维介质中的传播规律.随着该理论的逐步发展与完善,杜启振和李宾(2009)使用有限差分技术,对横向各向异性介质进行了三维仿真,取得了较好结果.王洋等(2015)提出了一种新的交错网格有限差分技术,并通过模拟退火法进行全局优化,不但有效压制了数值频散,而且提高了计算精度.
有限差分偏移成像方法以其原理简单和易于实现等优势在地震偏移成像领域得到了广泛应用,但在瞬变电磁拟地震成像领域的应用还相对较少,所以本文对有限差分法在瞬变电磁拟地震成像中的应用初做尝试.该方法通过将波动方程分解为上、下行波方程,经算子展开后,对上行波使用一级近似方程,然后利用有限差分方法求解近似方程,最后对虚拟波场向下延拓成像.本文主要分为以下几个部分:(1)简要介绍瞬变电磁虚拟波场的求解;(2)介绍有限差分偏移成像方法的基本原理;(3)使用理论模型与野外实测数据对本文方法进行验证.
1 基本原理
瞬变电磁扩散场主要描述的是低频电磁场传播过程中的扩散和感应特征,具有较强的体积效应,所以对电性界面的分辨能力较差;而波场能够比较好地反映地质界面信息.本节将对瞬变电磁扩散场到虚拟波场的求解和有限差分偏移成像方法进行描述.
1.1 瞬变电磁虚拟波场
在导电介质中,低频电磁场可忽略位移电流,且满足扩散方程.为了不失一般性,本文取f(x,y,z,t)表示瞬变电磁扩散场,并满足如下的扩散方程:
(1)
式中,μ为磁导率,σ(r)为电导率.设u(x,y,z,τ)为虚拟波场,满足如下的波动方程(Lee et al.,1989):
(2)
根据Lee等(1989)可知,瞬变电磁扩散场到虚拟波场的表达式为
(3)
公式(3)为第一类Fredholm型积分方程,该方程属于典型的不适定问题.对公式(3)进行线性离散,得
(4)
其中,
(5)
离散后得到的是高度病态的线性方程组,且随着线性方程组阶数的增加,矩阵的条件数会急剧增大(戚志鹏等,2013).
1.2 精细积分法求解瞬变电磁虚拟波场
对公式(3)线性化离散之后,得到的线性方程组具有严重的病态性.使用传统的求解方法较难得到高精度的虚拟波场,所以本文采用精细积分法(鲁凯亮等,2021)求解瞬变电磁虚拟波场.该方法通过将一个高度病态的线性方程组转换成求积分的过程,大大降低了解决病态问题的难度.积分步长以2的指数增加,具有较高的收敛特性.
从如下的病态线性方程组出发:
Au=f,
(6)
式中A为n阶正定矩阵,f为n维实向量.记H=-A,则公式(6)可以转化为
Hu+f=0.
(7)
根据一阶微分方程
(8)
线性方程组(7)和方程(8)分别可以看作瞬态和稳态热传导方程的表达式.方程(8)的解具有如下形式:
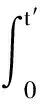
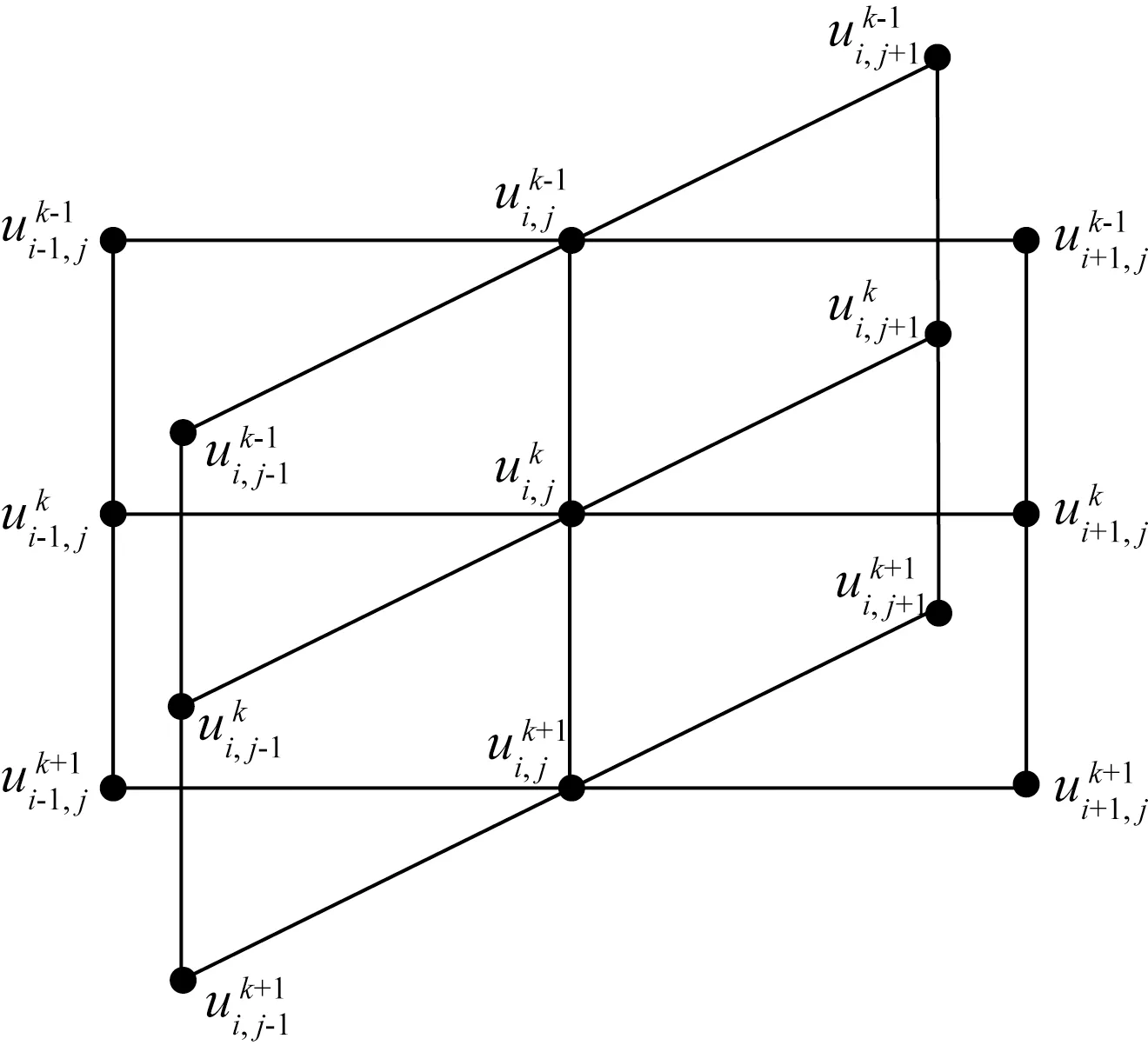
(9)
可以看出,当时间t′→∞时,exp(Ht′)→0,此时公式(9)中的积分项就无限趋近于线性方程组(7)的解,即
(10)

(11)
对公式(11)两边同时乘以f,得
u1=(I+exp(-Hζ))u0.
(12)
由于ζ是极小量,在计算矩阵指数函数时,可使用Taylor展开的前几项:
(13)
对公式(13)在区间[0,ζ]积分,得
(14)
则虚拟波场的初始值为u0=F(ζ)f.
令积分步长以2k-1ζ增长,则有
(15)
并且当2kζ→Fk时,有
(16)
公式(16)为虚拟波场的迭代公式(鲁凯亮等,2021).
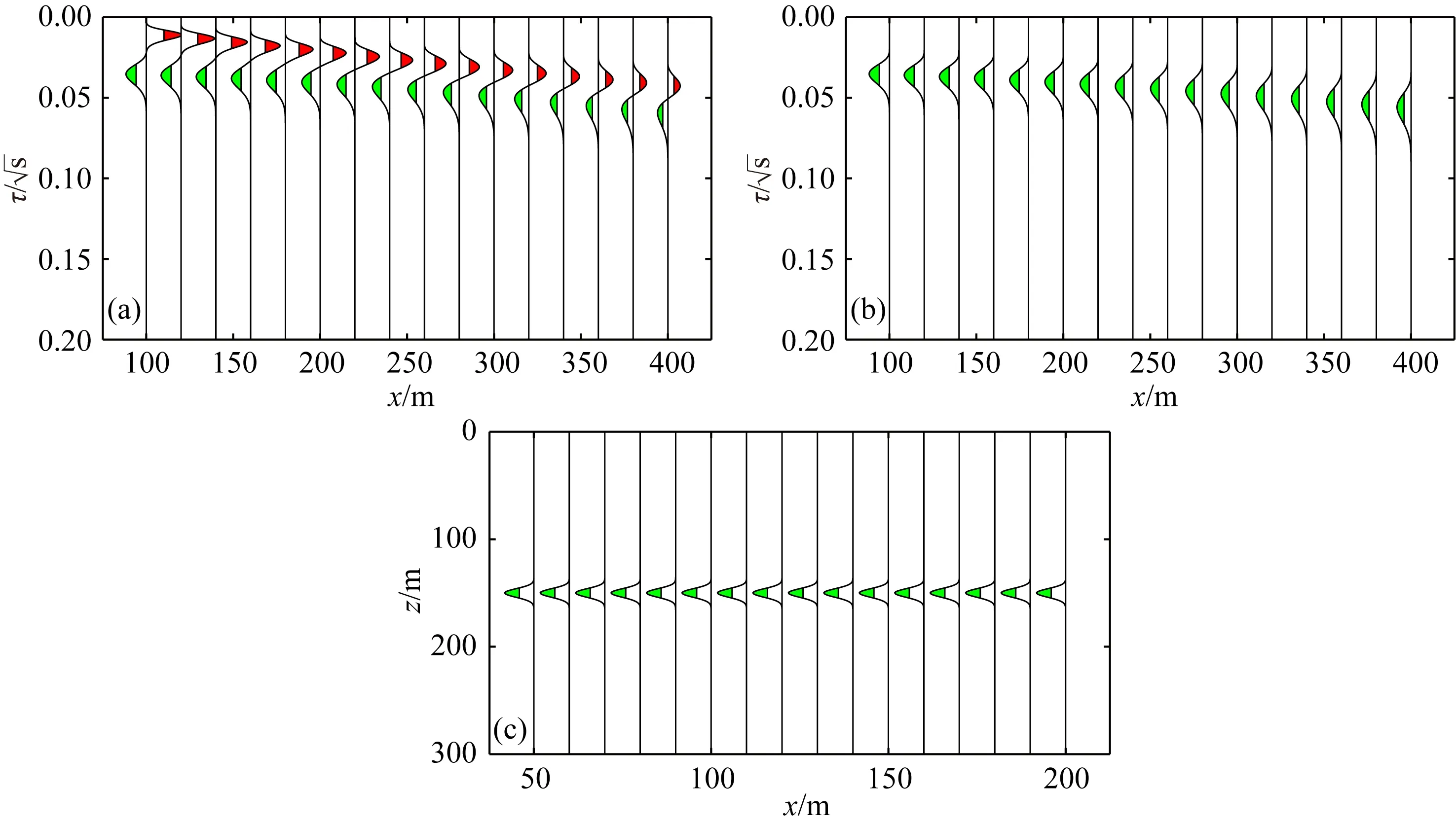
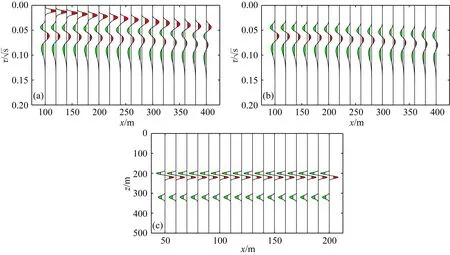
接下来以戚志鹏等(2013)文章中的例子对本文方法进行检验,并将结果与其进行对比.图1a为解析的虚拟波场,图1b为对应的瞬变电磁扩散场.图2是两种方法的计算结果与相对误差.从图2b可以看出,使用精细积分法的相对误差最高不超过2%,平均相对误差小于1%,从图2d可以看出,虚拟波场的相对误差较大.
图1 (a)虚拟波场;(b)对应的扩散场

图2 虚拟波场数值解与相对误差
1.3 有限差分偏移成像
1.3.1 二维有限差分偏移成像方法
在直角坐标系中,无源区波场所满足的标量波动方程为(马在田,1989)
(17)
采用上行波的一阶近似方程,将方程(17)写成二维波动方程
(18)
进而得到方程(18)在空间-时间域的一级近似方程:
(19)
式中的v可以是一个常数,也可以是x,z的函数.
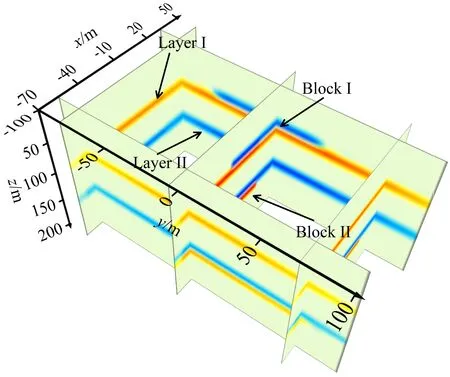
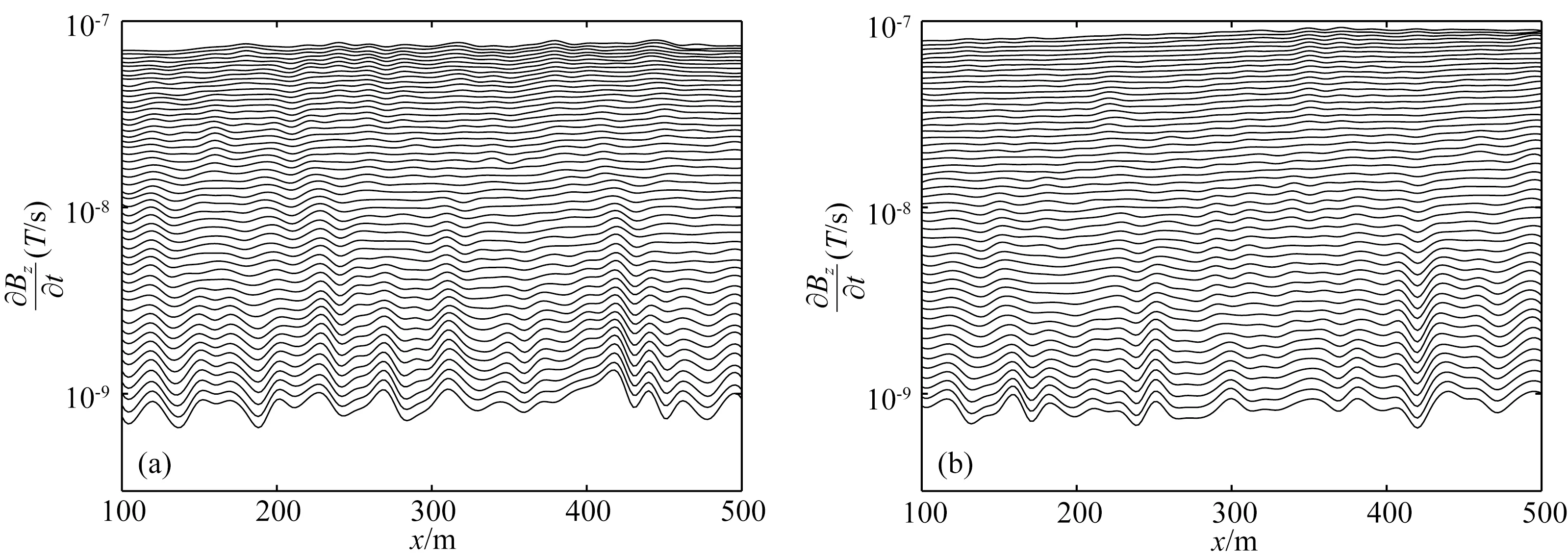
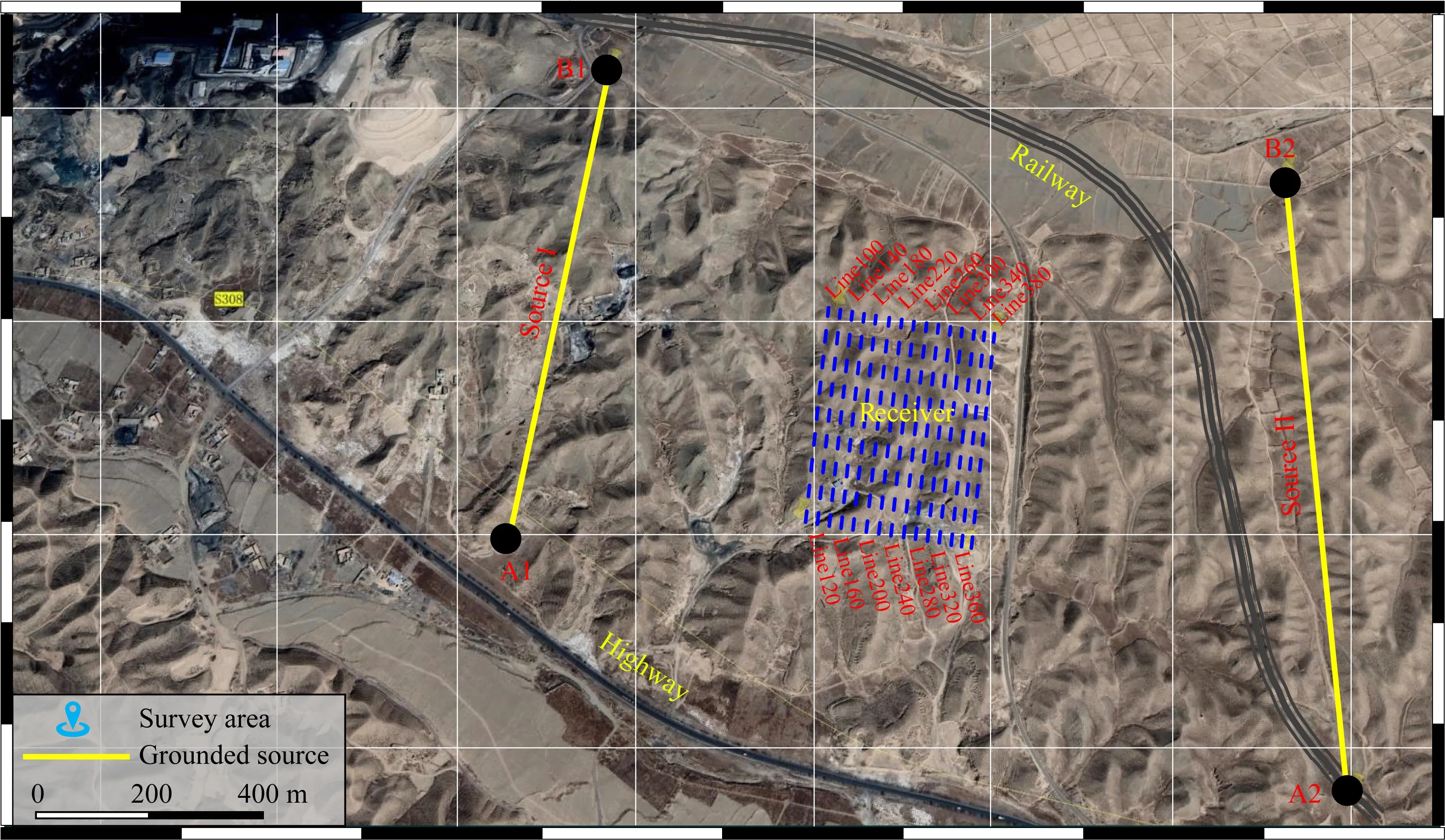
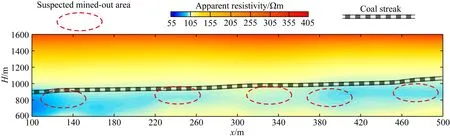
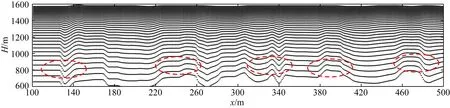
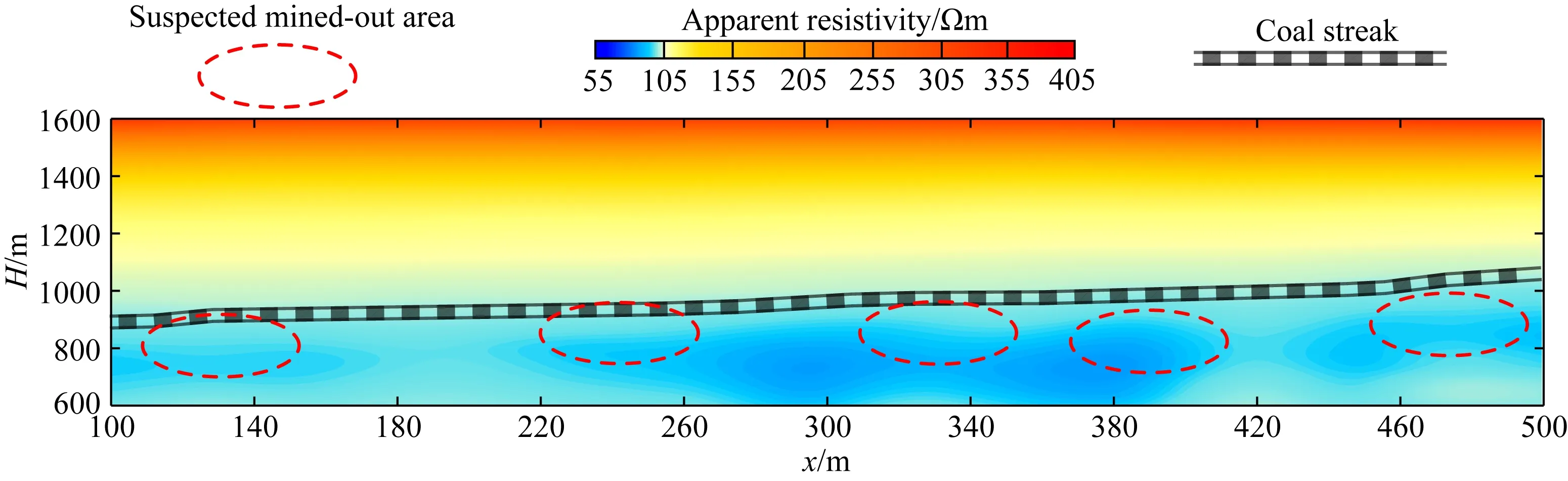
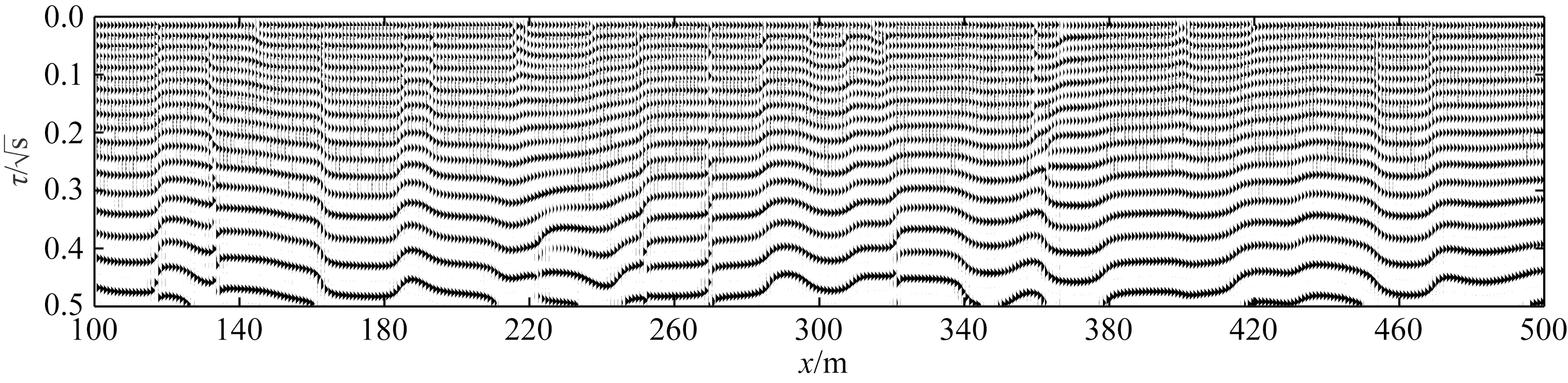
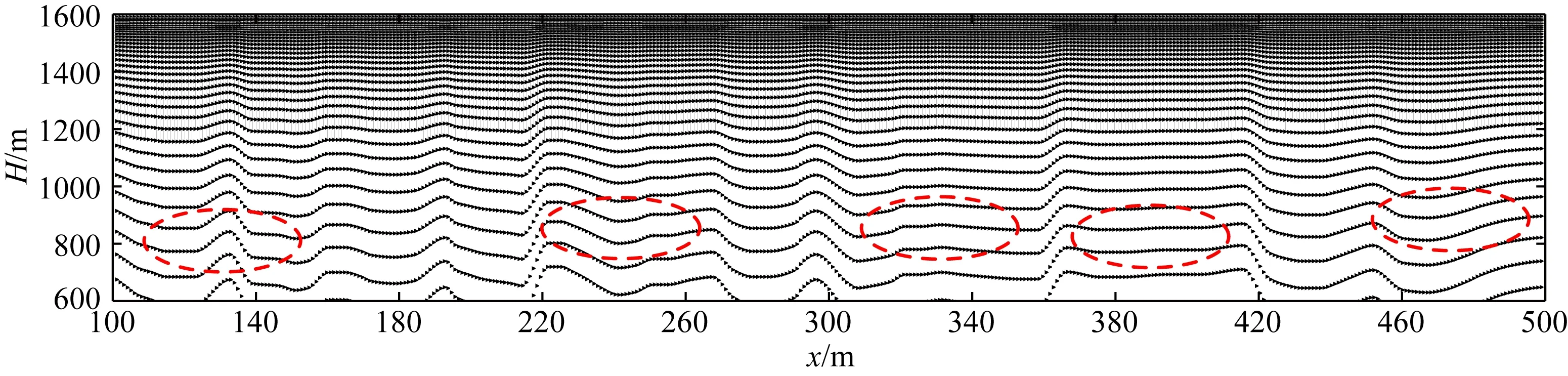
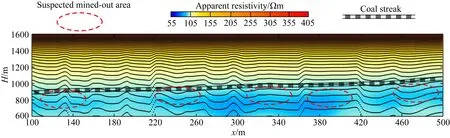
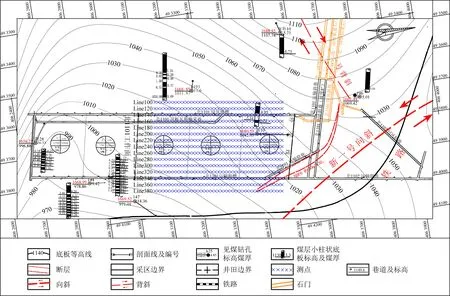
设公式(19)存在于空间Ω(-∞ (20) 式中u(x,z=0,t)=φ(x,t)为地面上观测到的波场.我们可以通过求解上述偏微分方程得到地表以下任何点(x,z>0)曾经出现过的上行波的波场值u(x,z,t). 本文采用对称隐式(Crank-Nicolson)的差分格式,可将待求解问题写成下面的矩阵形式: (21) (22) (23) (24) (25) 由于矩阵A为主对角线占优的矩阵,且α恒大于零,因此总有|1+2α|>2|α|,因而矩阵A的行列式不为零,即detA≠0,所以矩阵A可逆(马在田,1989). 1.3.2 三维有限差分偏移成像方法 在空间-时间域中三维波动方程表示为(马在田,1989): (26) 在浮动坐标系中,方程(26)如下所示: (27) 图3 三维差分格式示意图 并用下面的差商表示其他导数: (28) (29) (30) 式中的i,j,k,n分别表示x,y,t,z方向的样点号. 将公式(28)—(30)代入(27)式,得 (31) (32) 式中右端项为已知项. 本文假定Δx=Δy,则有α1=α2=α,β1=β2=β.因此,(32)式可简化为 (33) 式中的Bi,j是节点(i,j)上的值.(33)式可写成矩阵形式: IU+AU+UA=B, (34) (35) (36) (37) 则公式(34)可写成: U=-(AU+UA)+B, (38) 方程(38)可用迭代法求解,且迭代过程收敛(马在田,1989). 偏移成像是对反射波进行逆时归位的过程,在此过程中,直达波是一种无用信号,而且因为其能量强,会对偏移成像的结果造成较大干扰.因此,对直达波进行去除非常有必要,且由于波形拉伸效应,应该在偏移成像之前去除直达波.可通过公式(39)去除直达波: Ur=RU, (39) 式中,U为虚拟波场信号,Ur为去除直达波后的波场信号,R为消除函数, (40) 综上所述,有限差分偏移成像方法通过将波动方程分解为上、下行波方程,经算子展开后,再对上行波使用一级近似方程,然后利用有限差分偏移成像方法向下延拓求取地下各点各个时刻的波场值,最后取地下各点零时刻的波场值进行地下的构造成像.将电性源瞬变电磁数据的拟地震成像处理流程总结如下:(1)使用三维瞬变电磁正演或野外实际采集得到时间域的电磁场数据;(2)对扩散场的电磁数据进行去噪和圆滑后,使用精细积分法求解虚拟波场;(3)消除虚拟波场的直达波,从而消除其对偏移成像结果的影响;(4)在上述步骤的基础上,使用等效导电平面法进行速度建模(李貅等,2010),最后使用有限差分偏移成像方法,获得深度偏移剖面;(5)对于偏移成像结果,为了消除晚期数据的波形展宽效应,可使用振幅均衡与子波压缩技术进行处理(薛国强等,2011). 本文设计典型的地质模型来验证本文方法的正确性与有效性.首先使用瞬变电磁三维正演方法(Zhou et al.,2018)得到扩散场电磁信号,然后使用精细积分法得到虚拟波场,再对数据进行预处理,最后使用有限差分方法获得偏移成像剖面. 这一小节使用均匀半空间模型与层状模型验证本文方法的准确性.设置均匀半空间的电阻率为100 Ωm.D型模型的第一层与第二层电阻率分别为100 Ωm和10 Ωm,第一层的厚度为150 m.HK型模型的第一层介质厚度为200 m,电阻率为100 Ωm;第二层介质厚度为20 m,电阻率为10 Ωm;第三层介质厚度为100 m,电阻率为100 Ωm;第四层的电阻率为1 Ωm,向下无限延伸.设置接地导线源的长度为100 m,发射电流为1 A.发射源的坐标分别为(0 m,-50 m,0 m)和(0 m,50 m,0 m),接收点位于x轴上,起始坐标为(100 m,0 m,0 m),终止坐标为(400 m,0 m,0 m).测线长度为300 m,点距为20 m,共16个测点,接收的电磁信号为Ey. 图4为均匀半空间模型与对应的扩散场信号.图5为不同偏移距的均匀半空间的虚拟波场,从图可以看出,均匀半空间直达波的同相轴为一条直线.将瞬变电磁扩散场转换为虚拟波场后,符合波场的传播特征. 图4 (a)均匀半空间模型;(b)扩散场 图5 均匀半空间虚拟波场 D型模型 图6为D型模型示意图与对应的扩散场信号. 图6 (a)D型模型示意图;(b)扩散场 图7a为波场反变换的结果,图7b为消除直达波的结果,图7c是有限差分偏移成像的结果.从图7a中可以看出,有两个同相轴,红色同相轴为直达波,会对后续的偏移成像结果有较大影响,需要消除.从图7c中可以看出,在z=150 m的位置处存在振幅扰动,这与所设计的模型相符,证明了本文方法的正确性. 图7 D型模型计算结果 HK型模型 图8为HK型模型示意图与对应的扩散场信号.图9a为波场反变换的结果,图9b为消除直达波的结果,图9c是有限差分偏移成像的结果.本文设计的模型有三个界面,中间是一个低阻薄层,从图9c中可以看出,在z=200 m,z=220 m和z=320 m的位置处均存在振幅扰动,且这三个地层界面的位置与所设计的模型相符合,证明了本文方法的有效性. 图8 (a)HK模型示意图;(b)扩散场 图9 HK型模型计算结果 本文设计了图10所示的复杂采空区模型.该模型有两个低阻块状体,上层块状体的埋深为60 m,电阻率为1 Ωm,下层块状体的埋深为130 m,电阻率为0.1 Ωm.两个低阻块状体位于地层之中,地层从上到下分别为细砂岩、砂质页岩和石英砂岩.具体的模型参数见表1.本文采用课题组自行编写的三维正演程序计算瞬变电磁响应.剖分该模型的最小网格为10 m,网格扩大因子为1.35,三个方向的网格数为84×84×76.本文采用两条接地导线源,发射源端点处的坐标分别为(-100 m,-250 m,0 m)、(-100 m,250 m,0 m)和(100 m,250 m,0 m)、(100 m,-250 m,0 m),发射源的长度为500 m.在地面上选取三条测线,线号分别为Line140、Line200和Line240.三条测线与y轴平行,分别位于x=-60 m、x=0 m和x=40 m.选取这三条测线的原因是测线Line140在底部块状体正上方,测线Line200在两个块状体重叠部分的正上方,测线Line240在浅部块状体的正上方,其他位置的电磁响应与这三条测线类似.因为测线离发射源较近时,电磁信号的强度较大,所以当发射源I激发时,测线Line140接收电磁信号,当发射源II激发时,测线Line200和Line240接收电磁信号. 图10 复杂采空区模型示意图 表1 复杂采空区模型参数 图11a、b和c依次为测线Line140、Line200和Line240的多测道曲线.测线Line140位于x=-60 m处,从图11a可以看出,晚期的多测道曲线有明显的“上凸”现象,表明该位置处有一明显的低阻异常.测线Line200位于x=0 m处,从图11b可以看出,在多测道曲线上有两处低阻异常体引起的异常.图11b中浅部的低阻异常较小,深部的低阻异常较大,并且浅部异常体的电导率较弱,导致图11b中晚期比早期的电磁异常明显.测线Line240位于x=40 m处,从图11c可以看出,早期的多测道曲线有微弱的“上凸”现象,表明在该测线的下方有一块低阻异常体.图11的三条测线均能体现出低阻异常体引起的电磁异常,说明瞬变电磁法对低阻异常体的探测是有效的,但是同时也可以发现,瞬变电磁法对地质异常体的界面刻画较弱,很难直接得到地质异常体的界面信息,所以本文通过瞬变电磁扩散场计算虚拟波场,提高瞬变电磁法对地质异常体界面的分辨能力. 图11 多测道曲线 图12a、b和c依次为测线Line140、Line200和Line240的虚拟波场,每条测线的第一个红色同相轴为直达波,其余同相轴为地层界面信号.从图12可以看出,测线Line140刻画了两个地层界面以及底部低阻异常体的界面.测线Line200刻画了两块低阻异常体的界面以及两个地层界面.测线Line240刻画了两个地层界面以及浅部低阻异常体的界面.但是瞬变电磁的虚拟波场只能粗略反映地层的界面形态,无法准确得到地质异常体的界面位置.接下来本文使用有限差分偏移成像方法来获取地质界面的准确位置. 图12 虚拟波场 图13a、b和c依次为测线Line140、Line200和Line240的偏移成像结果.通过计算可以得知,测线Line140下方有三个地质分界面,其中前两个同相轴反映了两个地层界面的位置以及形态,第三个同相轴反映了底部低阻异常体的界面位置.测线Line200下方有四个地质分界面,其中前两个同相轴反映了浅部低阻异常体的界面以及第一个地质界面的位置,后两个同相轴反映了第二个地质界面以及深部低阻异常体的界面位置.测线Line240反映了浅部低阻异常体的界面位置和第二个地层界面的位置.从图13可以看出,同相轴所表示的深度与设计的理论深度相符.图14为三维偏移成像结果,从图中可以清晰地看到异常体与地质界面的形态与位置.通过以上理论模型的计算,本文在得到瞬变电磁虚拟波场的基础上,通过有限差分偏移成像技术,可以较为准确地得到地质界面的深度.接下来本文对煤矿采空区实测数据进行处理. 图13 偏移成像 图14 三维偏移成像结果 魏家地煤矿位于甘肃省白银市平川区宝积镇东部约7 km处,处于靖远煤田宝积山矿区东部魏家地井田内,西北与宝积山煤矿相接,西南与大水头煤矿为邻.魏家地煤矿所在的宝积山矿区,地处宝积山盆地的东南部,矿区大部分基岩裸露;盆地内西部、东北部和东南部多为低矮的丘陵,主要为剥蚀堆积地貌,除有少部分基岩出露外,大部分被黄土所覆盖.矿区的开阔平缓地带多为第四系冲积松散沉积层.工作区域地表北部开阔平缓,被黄土覆盖,大多为农田及低矮丘陵;在采区的中部、北部有两条季节性沙河.矿区水文地质条件较简单.地表气候干燥,年平均降雨量为238.2 mm,无常年性地表水流和地表水体,雨季期间洪水从两条季节性沙河流过.矿井含水层为富水性极弱的粗碎屑砂岩,各含水层之间又有良好的隔水层(粉砂岩、泥质粉砂岩、泥岩、砂质泥岩、煤层),互相水力联系较弱.工区主要含煤地层由灰白色石英细砂岩、砂砾岩、炭质泥岩、炭质粉砂岩组成. 图15为该工区的野外地貌特征,从图中可以看出,该地区地势较为平缓,高差起伏较小,地表存在较多空洞.图16为180号测线和380号测线的多测道曲线,早期的多测道曲线较为平滑,中晚期的多测道曲线对深部地层信息有较为丰富的反映. 图15 野外地貌特征 图16 多测道曲线 本次试验的观测系统布置如图17所示,探测试验采用凤凰V8多功能电法仪,为提高勘探深度,增强有用信号,最大程度获取地下采空区的异常信号,发射系统是两个长度为1 km的接地长导线源,激发脉冲是基频为8.3 Hz、占空比为1∶1的矩形波脉冲,发射电流强度为15 A.接收装置为地面回线框,在地表采集了二次场的垂直磁场分量.本次的试验数据采用了面积式测网采集,累计15条测线,每条测线长度 400 m,测线之间的距离为20 m,总的测线长度达到6 km,每条测线上的测点间距为10 m. 图17 采空区试验观测系统布置图 图18 工区Line180号测线视电阻率图 图18为工区Line180号测线的视电阻率,可以看出,在x=130 m、x=240 m和x=340 m以及x=390 m和x=470 m处疑似积水采空区.推断可能是因为煤矿采空区塌陷,导致地层中裂隙比较发育,形成富水区域,从而形成低电阻率异常区域.图19和图20分别为工区Line180号测线的虚拟波场和有限差分偏移成像图,从偏移成像结果可以看出,在测线的120~160 m、160~190 m、220~260 m、320~360 m以及370~420 m和460~490 m处,推测地层的错断比较严重,可能是由于煤层被开采,在偏移成像图上表现出横向不连续、间断跳跃的特征.图21为Line180号测线的视电阻率与偏移成像对比图,可以看出,低电阻率区域与偏移成像横向不连续处对应较好. 图19 工区Line180号测线虚拟波场 图20 工区Line180号测线有限差分偏移成像结果 图21 工区Line180号测线视电阻率与偏移成像 图22为工区Line380号测线的视电阻率,可以看出,在x=140 m、x=220 m、x=300 m、x=380 m和x=460 m处呈现出明显的低电阻率区域,疑似积水采空区.并且通过对比图18和图22可以发现,图22在x=460 m处的低电阻率特征更为明显.通过图28可知,在工区的北侧存在断层,地层错断可能更为严重,有可能造成更多的富水区域.图23和图24分别为工区Line380号测线的虚拟波场与有限差分偏移成像图.图25为Line380号测线的视电阻率与偏移成像对比图,在低电阻率特征明显的区域,偏移成像的同相轴变化比较明显,推断地层不连续,裂隙发育,形成富水区域.图26是工区的3D视电阻率与成像结果,可以看出,视电阻率的低阻异常区域与偏移成像的同相轴错断特征较为吻合,通过三维图可以直观地圈定出可能存在含水采空区的位置,为后续的工程项目提供潜在的灾害突发信息.本文通过视电阻率与偏移成像的联合解释,证明了本文方法的有效性. 图22 工区Line380号测线视电阻率图 图23 工区Line380号测线虚拟波场 图24 工区Line380号测线有限差分偏移成像结果 图25 工区Line380号测线视电阻率与偏移成像 图26 工区三维视电阻率与偏移成像 图28是工区煤层底板等值线图,可以看出,工区的煤层底板等高线约为1000 m(同时从图上的钻孔数据可知,钻孔的煤层高程约为1000 m,图27所示),在该区域的北侧,有一断层斜插工区.这些特征与视电阻率结果较为吻合.此外,本文的计算结果与已知的地质资料较为相符,说明本文的偏移成像方法在识别地层特征、电性界面方面有较好的效果. 图27 钻孔信息 图28 工区煤层底板等值线图(鲁凯亮等,2021) 瞬变电磁扩散场转化到虚拟波场是一个典型的不适定性问题,使用精细积分法可以将一个病态线性方程组的求解转化成一个求积分的稳定过程,极大地提高了求解虚拟波场的精度以及稳定性. 将瞬变电磁扩散场转换为虚拟波场后,使用有限差分方法得到了瞬变电磁虚拟波场的深度偏移成像剖面,实现了对电性界面快速成像的目的.测试结果表明:本文所使用的有限差分偏移成像方法,能够对地下的电性介质界面进行准确成像.并且本文通过对实测数据的处理,进一步说明本文方法在识别电性界面与地层特征方面的可行性,为瞬变电磁高分辨成像打下了较好的基础. 在后续的工作中,可以引入窗口扫时、相关叠加以及微分脉冲激发等技术,进一步提高瞬变电磁偏移成像的精度与分辨力. 致谢感谢评审专家和编辑提出的宝贵修改意见.
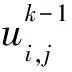

1.4 切除直达波技术
2 方法验证
2.1 均匀半空间与层状模型


2.2 复杂采空区模型





2.3 野外实测数据处理





3 结论
