长初级双边直线感应电动机分段推力协同控制和测速算法

张明远 史黎明 范满义 周世炯 朱海滨

长初级双边直线感应电动机分段推力协同控制和测速算法

张明远1,2史黎明1,2范满义1,2周世炯1,2朱海滨1,2

（1. 中国科学院电力电子与电力驱动重点实验室（中国科学院电工研究所） 北京 100190 2. 中国科学院大学 北京 100049）

为提高分段长初级双边直线感应电动机（LP-DSLIM）的推力平稳性，提出一种多变流器驱动的分段推力协同控制策略和测速算法。基于分段LP-DSLIM单元电机数学模型，研究了一台变流器控制一段单元电机的特性，设计了多变流器驱动多段电机的协同控制策略；根据直线电机运动方程和多分段LP-DSLIM推力计算值构造了线性扩张状态观测器（LESO）以观测速度，速度观测值噪声小且无滞后，用于推力协同控制时推力波动小且无推力损失，有效地改善了推力控制效果。仿真和实验验证了推力协同控制策略和LESO测速算法的有效性。

长初级双边直线感应电动机 多变流器驱动 推力协同控制 测速算法 线性扩张状态观测器

0 引言

长初级双边直线感应电动机（Long Primary Double-Sided Linear Induction Motor, LP-DSLIM）推重比大，在高速运行时边端效应小，因而被广泛用于轨道交通牵引和直线电机加速等领域[1-5]。由于LP-DSLIM漏感大，在实际工程应用中为了降低驱动变流器的电压和容量、提高功率因数，通常将长初级进行分段供电[6]。

现有文献大多研究长初级分段串联供电方式[7-8]。串联供电由一台逆变器供电，必须在电流过零点切换保证电流连续，供电网络复杂、对切换开关要求高，切换时会产生电流尖峰和较大的推力冲击[9-10]。为了降低对切换开关的要求、提高可靠性，可采用多台变流器供电的方式，与次级耦合的各段电机分别由一台变流器独立驱动[11]，次级推力为多段电机推力之和。

分段LP-DSLIM的每段初级及其耦合的次级都是一段单元电机，单元电机的状态和参数随耦合的次级长度变化。文献[12-13]建立了中单元电机模型，但此单元电机模型的次级磁链和推力滞后现象较为严重。文献[14]引入虚拟次级建立了一种新型单元电机数学模型。相较于传统模型[12-13]，新型单元电机模型描述次级过分段时的单元电机特性更加准确，解决了磁链和推力滞后问题。但是，目前尚未对多逆变器控制分段LP-DSLIM的推力表征方法和高性能协同控制策略进行研究。

另外，速度信息是直线感应电机牵引控制的一个必要条件，速度的精度决定了控制性能[15-16]。因为高速直线驱动领域速度信号难以直接测量，因此首先要得到位置信号。

在旋转电机中，编码器与转子同轴做旋转运动。旋转编码器光栅数通常有1 024、2 048、4 096等，分辨率和测速精度较高，通常使用M法、T法或M/T法进行测速。M法是通过对编码器在一定的时间内输出的脉冲个数计数来计算速度，适合用于高速运行；T法是测取编码器两个输出脉冲之间的时间间隔来计算速度，适合用于低速段；M/T法综合了M法和T法的特点，在低速和高速都具有较高的测速精度[17]。

LP-DSLIM的速度测量设备与旋转电机区别较大，旋转电机的测速算法不再适用于LP-DSLIM。LP-DSLIM的初级绕组、供电系统和控制系统均固定在地面，位置测量设备也最好固定在初级基座上，以尽量减少速度信号传输的时延。常用的实时位置测量方法通常有激光测距[18]和光栅定位[19]两种。激光测距得到的位置信号是连续的，但受环境影响较大，测量结果中存在噪声，经过微分运算，真实的速度信息可能被淹没在噪声中，无法用于电机控制。光栅定位没有噪声，但位置信号是离散的，绝对精度与光栅的宽度、加工均匀性等有关。受到机械强度和激光器光斑大小的限制，直线光栅宽度较大，因此M法不再适用。受到机械加工精度和机械振动的影响，T法也不再适用。

目前针对此类LP-DSLIM测速的研究较少，不管是激光测距还是光栅定位，都需要使用合适的微分算法或其他测速算法来获取速度。韩京清等提出跟踪微分器（Tracking-Differentiator,TD）的思想，给出了非线性跟踪微分器的一般形式，对其信号跟踪命题给出了严格的证明[20]。文献[21]利用二次时间最速系统提出了一种离散形式的TD，具有快速跟踪输入信号、无超调、无颤振的特性，能得到较好的微分信号。但是TD用于测速时，观测速度存在噪声大或滞后严重的问题，影响推力的控制效果。

本文基于新型单元电机模型[14]推导多逆变器驱动的分段LP-DSLIM的推力协同控制策略，根据直线电机运动方程和多分段LP-DSLIM推力计算值构造一种速度观测器，对标效果比较好的TD测速算法，对两种测速算法进行分析对比，通过仿真和实验对提出的推力协同控制策略和测速算法进行了验证。

1 单元电机模型

单元电机示意图如图1所示。1为每段初级长度，D为耦合次级的长度。定义耦合因数为α=D/1。耦合因数在0～1之间变化。当D=1时，单元电机为全耦合。全耦合时，初级电阻为s，初级自感为s，次级电阻为r，次级自感为r，励磁电感为m。

图1 单元电机示意图

在静止两相αβ轴系下，第段单元电机的电压和磁链方程[14]为

式中，s()、s()和s()分别为第段单元电机初级电压矢量、电流矢量和磁链矢量；r()、r()和ro()分别为第段单元电机次级电压矢量、电流矢量和磁链矢量；r()为次级磁链中间过渡量；r=π/，为极距，为次级速度；为微分算子。

第段单元电机产生的电磁推力为

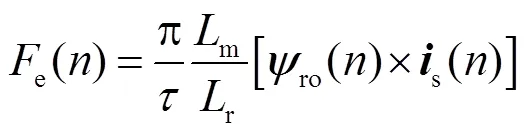
由式（1）推导得到次级磁链状态方程为

同步旋转dq轴系与静止两相αβ轴系的矢量变换关系为

式中，上标e表明该矢量是同步旋转dq轴系中的矢量；e为同步旋转dq轴系相对于静止两相αβ轴系的角度。

将式（4）代入式（1）和式（3），得到同步旋转dq轴系下次级磁链状态方程为

式中，r为次级时间常数，r=r/r；e为同步旋转dq轴系的角速度，e=e。

同步旋转dq轴系下，第段电机的电磁推力为

2 多变流器协同控制策略

变流器的数量不小于次级最多耦合的初级段数。同一时刻，1台变流器仅给1段电机供电，与次级耦合的多段电机共同出力。以两台变流器供电为例，电机奇数段初级和偶数段初级通过反并联晶闸管或其他开关分别连接到变流器1和变流器2，系统拓扑如图2所示。若有三台及以上变流器时，供电拓扑依此类推。

图2 多变流器驱动分段LP-DSLIM拓扑

为实现多段电机之间的推力协同控制，本节首先研究了一台变流器控制一段单元电机的特性，然后设计了多变流驱动多段电机的协同控制策略。

各段电机是相互独立的，每段电机都有各自的同步旋转dq轴系。将各段电机的dq轴系沿其次级磁链定向，将式（5）分解为dq轴分量可得

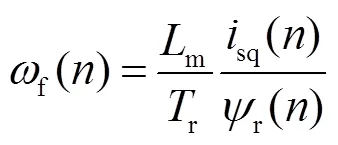
式中，f()为转差角频率。

次级磁链的角速度为

电磁推力为

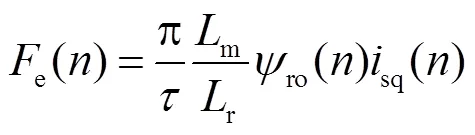
将式（7）代入式（10）中，电磁推力被整理为

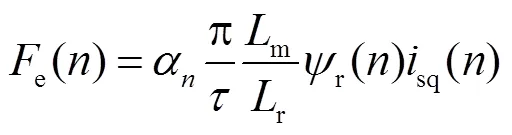
为保证次级进入一段电机时该段电机已建立起磁场，在次级进入该段之前该段电机提前供电。分析式（7）可知，r()与sd()是一阶惯性环节。如果sd()是常数，只要提前供电时间大于3r，就可以认为r()=msd()。式（11）改写为

假设共有段电机，当所有单元电机的初级d轴电流都等于sd、q轴电流都等于sq，所有电机的总电磁推力为

式中，2为次级长度。

由式（12）和式（13）可以推导得到各段电机的分推力和总推力的关系为

由式（14）可知，各段电机的推力与耦合的次级长度成正比。

所有单元电机共用一个次级，因此各段电机次级速度是相同的。根据式（8）和式（9）可知，所有单元电机次级磁链矢量的角速度是相等的，因此所有单元电机的同步旋转dq轴系也是重合的。总次级磁链的幅值ra为

从式（13）和式（15）可以发现：当所有单元电机的初级d轴电流都等于sd、q轴电流都等于sq时，多变流器供电的分段并联LP-DSLIM的次级磁链方程和电磁推力方程与旋转感应电机类似。当sd为恒定值时，次级磁链幅值r也是恒定值，次级总推力可以由sq控制，各段电机的分推力自然地与耦合的次级长度成正比，实现了多变流器供电的分段并联LP-DSLIM推力协同控制。

3 测速算法

在LP-DSLIM测速系统中，采集到位置信号后，对位置进行微分才能得到速度信号。

3.1 基于跟踪微分器的测速算法

“跟踪微分器”的离散形式[22-23]为

式中，为跟踪微分器的输入；1跟踪；2为1的微分，是的近似微分；为采样时间，表示离散系统的第步；(·)为“快速控制最优综合函数”，计算过程如下：

(·)中有两个可调参数和0。为“速度因子”，决定跟踪速度，越大跟踪速度越快，但当被噪声污染时，会使信号1被更大的噪声所污染；0为“滤波因子”，对噪声起滤波作用，0越大，就会使1跟踪信号的滞后越严重[23]。为取得较好的微分效果，要同时兼顾噪声和滞后，需要权衡选取和0。

3.2 基于构造速度观测器的测速算法

直线电机运动方程为

式中，为位移；为速度；为加速度；e为电机的电磁推力；l为阻力；为次级和负载质量之和。

根据式（12）可以计算出一个近似准确的次级总推力ecal。

由于参数误差和边端效应造成计算的推力和真实推力之间有一个误差Δe，因此将真实电机推力分成两个部分。

运动方程可以重新整理为

式中，Δ为实际加速度和计算加速度之间的差值，Δ=(Δe-l)/。

在电机系统中，Δ是有界且可微的，Δ=()，()也是一个有界值。将Δ扩张成一个新的状态变量，式（21）即为

设计线性扩张状态观测器（Linear Extended State Observer，LESO）[23-24]为

式中，1为位移的观测值；2为速度的观测值；3为参数误差、边端效应和阻力造成的加速度误差估计值；1、2和3为观测器的增益，通过选取适当的观测器增益，可以快速观测各状态量。

实际值和观测值之间的差值为

将式（22）减去式（23），误差方程为

其中

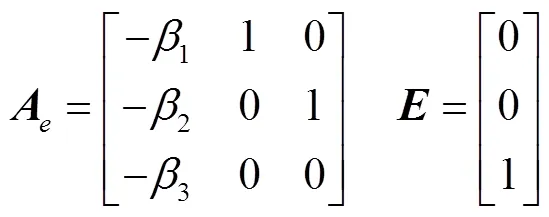
误差方程的特征方程为

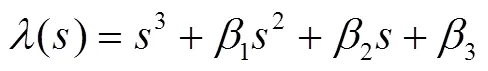
如果特征方程的特征值全部在复平面的左半平面，那么LESO是有界输入有界输出（Bounded-Input Bounded-Output, BIBO）稳定[25]。为了简单且便于配置极点，将观测器的3个极点配置在-0[26]。

解得

速度观测器算法简单，只需要配置一个参数。通过选取合适的0可快速跟踪速度真实值。

4 控制系统

图3 推力协同控制系统框图

5 仿真和实验

表1 全耦合单元电机参数

Tab.1 The parameters of unit motor in full coupling

（续）

LESO的0取20rad/s，TD的取100 000、0分别取0.01和0.1。仿真和实验中均取以上参数，仿真在PSIM中运行，在仿真控制系统中的位移信号中加入±0.02m的噪声。

5.1 仿真结果

基于LESO测速的推力协同控制仿真结果如图4所示。在图4中，三段电机A相电流平滑，两台变流器控制的dq轴电流能较好地跟随给定值。采用LESO测速算法时，观测速度可以较好地跟踪真实速度，噪声小且无滞后，速度误差小于0.06m/s，采用LESO观测速度进行磁场定向可以获得较好的定向效果。耦合因数表明次级与单元电机的耦合情况，各段电机的推力与耦合的次级长度成正比，总推力基本为恒定值，推力波动小，实现了较好的速度观测和多变流器控制多段电机的推力协同控制效果。

基于TD（0=0.01和0.1）测速的推力协同控制仿真结果分别如图5和图6所示。当0=0.01，速度观测的噪声较大，约为0.3m/s。较大的速度噪声使得磁场定向也有较大误差，导致较大的推力波动。当0=0.1时，噪声显著较小，但滞后严重，滞后时间约为0.2s，速度误差约为0.5m/s，此时输出推力仅为44N，小于0=0.01时的输出推力51N，推力损失为7N。这是因为若观测速度小于真实速度，那么实际转差频率小于转差频率给定值，导致输出推力下降。图6c中0.4s时出现了一个推力尖峰，原因是初始时速度观测误差小、推力大，随着速度的增大，速度观测误差越来越大，推力逐渐减小。

图6 基于TD(h0=0.1)测速的推力协同控制仿真结果

分别从测速噪声、滞后时间、测速误差、推力波动和推力损失多个方面对比基于LESO、TD(0=0.1)和TD(0=0.01)的仿真结果见表2。

表2 仿真结果对比

Tab.2 Comparison of simulation results

当TD的0较小时，观测速度噪声大，推力波动大；当TD的0较大时，观测速度滞后严重，推力损失大。采用LESO测速算法时，能同时满足观测速度噪声小和无滞后，测速误差小，用于控制时推力波动小且无推力损失。

5.2 实验结果

多变流器驱动分段LP-DSLIM实验平台如图7所示。实验平台的电机参数和控制目标与仿真中相同。实验中激光测距传感器受环境影响较大，模拟量采样又会引入采样噪声，次级运动过程中的测距噪声大于仿真系统中加入的噪声。加速度传感器实时测量负载加速度以反映推力。实验中使用三段电机，次级完全进入第三段电机后停止供电，停止供电后为自由滑行阶段。

图7 分段协同驱动控制LP-DSLIM实验平台

基于LESO测速的推力协同控制实验结果如图8所示。三段电机A相电流在起动和加速过程均较为平滑。与次级耦合的两段电机的dq轴电流控制效果较好，均按照设定的目标运行。加速Ⅰ段加速度斜坡上升，切换到加速Ⅱ段时没有加速度尖峰。自由滑行时加速度反映了轨道的摩擦和碰撞，这部分的加速度波动约为0.4m/s2。加速Ⅱ段的加速度波动约为0.6m/s2，这其中包含了轨道摩擦和碰撞的影响，因此实际电磁推力波动小于图8d中的加速度波动。

图8 基于LESO测速的推力协同控制实验结果

重复以上实验，即LESO测速结果用于推力协同控制时，将TD在0=0.01和0.1时的测速结果与LESO的观测速度进行对比如图9所示。0=0.01时，TD与LESO的测速结果基本拟合，但TD噪声较大。0=0.01时，TD噪声明显减小，测速结果平滑，但滞后于LESO，速度误差约为0.5m/s，与图5和图6相关仿真结果一致。

图9 LESO与TD测速结果对比

基于TD（0=0.01和0.1）测速的推力协同控制实验结果分别如图10和图11所示。图10中，速度计算噪声较大，由加速Ⅰ段切换到加速Ⅱ段时产生了0.3m/s2的加速度尖峰。加速Ⅱ段的加速度波动约为0.8m/s2，大于采用LESO测速的加速度波动。图11中，速度计算噪声小，由加速Ⅰ段切换到加速Ⅱ段时同样产生了0.3m/s2的加速度尖峰，与图6c仿真结果对应。值得注意的是，图11b中加速度平均值相较于图8d和图10b减小了0.4m/s2，按照次级和负载质量之和为17kg折合到推力损失约为6.8N，与仿真结果中7N的推力损失一致。

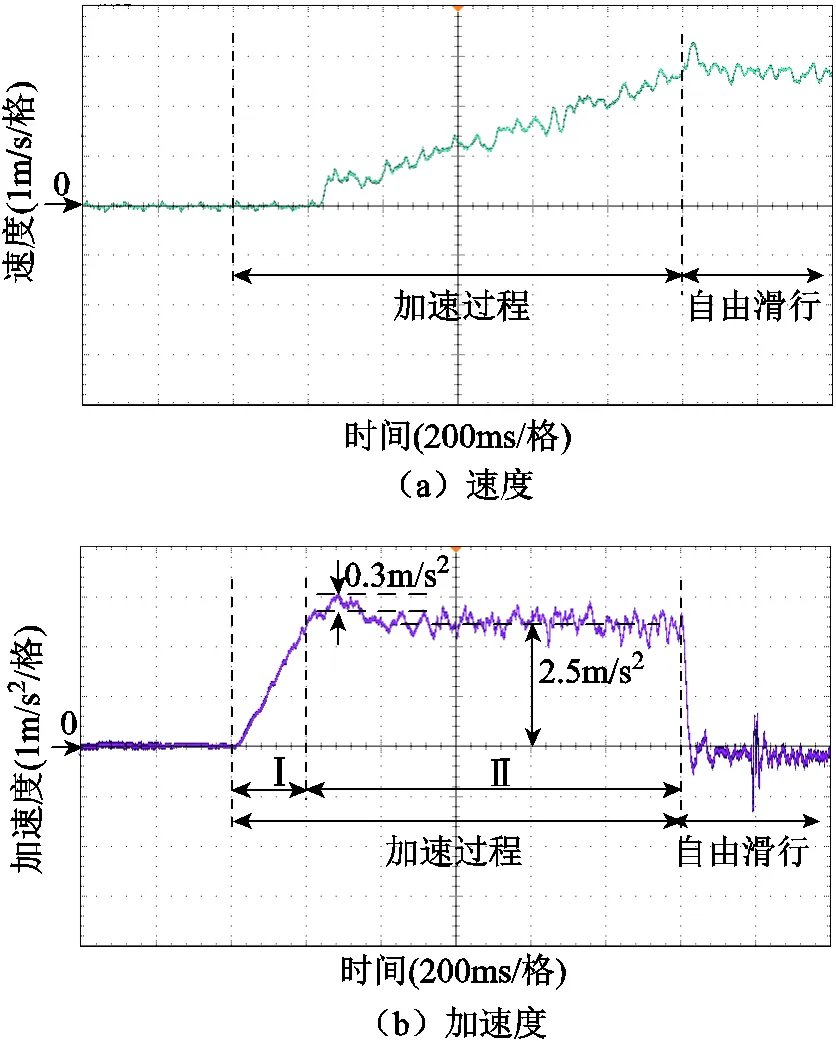
图10 基于TD(h0=0.01)测速的推力协同控制实验结果

图11 基于TD(h0=0.1)测速的推力协同控制实验结果

使用TD测速时，若0较小，计算速度滞后小，但是噪声较大，速度噪声大会增大控制系统的不稳定性。增大0，可以减小计算速度的噪声，但计算速度滞后大，会导致输出推力下降。另外使用TD时，由加速Ⅰ段切换到加速Ⅱ段会出现明显的加速度尖峰。而使用LESO测速时，参数易于调节，速度噪声小且无滞后，因而控制系统稳定性好、无输出推力损失，且加速Ⅰ段切换到加速Ⅱ段未出现加速度尖峰，加速Ⅱ段推力波动小，因此LESO测速算法具有明显的优势。

6 结论

基于单元电机模型推导得到了多逆变器驱动的分段LP-DSLIM的推力协同控制策略。根据直线电机运动方程和多分段LP-DSLIM推力计算值构造了一种速度观测器（LESO），并与TD测速算法进行对比。结论如下：

1）在多变流器驱动下，所有单元电机的初级d轴电流都等于sd、q轴电流都等于sq，sd控制次级磁链，sq控制次级电磁推力，各段电机的推力与耦合的次级长度成正比，实现了多段电机的推力协同控制。

2）构造的LESO速度观测器算法简单，噪声小，无滞后，LESO测速算法用于推力协同控制时的推力控制效果优于TD测速算法。

[1] Ma Weiming, Lu Junyong. Thinking and study of electromagnetic launch technology[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1071-1077.

[2] 张千, 刘慧娟, 马杰芳, 等. 考虑后退行波的长初级双边直线感应电机电磁性能计算[J]. 电工技术学报, 2020, 35(7): 1398-1409.

Zhang Qian, Liu Huijuan, Ma Jiefang, et al. Calculation of electromagnetic performance for long primary double sided linear induction motors considering backward traveling wave[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1398-1409.

[3] 徐伟, 肖新宇, 董定昊, 等. 直线感应电机效率优化控制技术综述[J]. 电工技术学报, 2021, 36(5): 902-915, 934.

Xu Wei, Xiao Xinyu, Dong Dinghao, et al. Review on efficiency optimization control strategies of linear induction machines[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 902-915, 934.

[4] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.

Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3182-3190.

[5] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012.

Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.

[6] 张明元, 马伟明, 何娜. 长初级直线电动机分段供电技术综述[J]. 中国电机工程学报, 2013, 33(27): 96-104, 14.

Zhang Mingyuan, Ma Weiming, He Na. Application of block feeding methods in long primary linear motors[J]. Proceedings of the CSEE, 2013, 33(27): 96-104, 14.

[7] 鲁军勇, 马伟明, 许金. 高速长定子直线感应电动机的建模与仿真[J]. 中国电机工程学报, 2008, 28(27): 89-94.

Lu Junyong, Ma Weiming, Xu Jin. Modeling and simulation of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(27): 89-94.

[8] 李卫超, 胡安, 马伟明, 等. 新型长定子直线感应电机闭环控制策略[J]. 中国电机工程学报, 2010, 30(增刊1): 226-231.

Li Weichao, Hu An, Ma Weiming, et al. Control strategy of a novel double-sided long primary linear induction motor[J]. Proceedings of the CSEE, 2010, 30(S1): 226-231.

[9] 马名中, 马伟明, 范慧丽, 等. 长初级直线感应电机分段供电切换暂态过程[J]. 电机与控制学报, 2015, 19(9): 1-7.

Ma Mingzhong, Ma Weiming, Fan Huili, et al. Switch transient process of section powered long-primary linear induction motor[J]. Electric Machines and Control, 2015, 19(9): 1-7.

[10] 张明元, 马伟明, 徐兴华, 等. 一种考虑电流过零的直线电机分段供电策略[J]. 海军工程大学学报, 2019, 31(4): 11-16.

Zhang Mingyuan, Ma Weiming, Xu Xinghua, et al. A block feeding strategy for linear motor considering switching at current-crossing point[J]. Journal of Naval University of Engineering, 2019, 31(4): 11-16.

[11] 孙晓. 多模块双边直线感应电机控制策略研究[D]. 北京: 中国科学院大学, 2018.

[12] 张志华. 分段式长初级双边直线感应电机特性研究[D]. 北京: 中国科学院大学, 2014.

[13] Sun Xiao, Shi Liming, Zhang Zhihua, et al. Thrust control of a double-sided linear induction motor with segmented power supply[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4891-4900.

[14] 张明远, 史黎明, 郭科宇, 等. 分段长初级双边直线感应电动机建模分析[J]. 电工技术学报, 2021, 36(11): 2344-2354.

Zhang Mingyuan, Shi Liming, Guo Keyu, et al. Modeling and analysis of segmented long primary double-sided linear induction motor[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2344-2354.

[15] 王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 2版. 北京: 机械工业出版社, 2014.

[16] 罗成, 李孺涵, 杨凯, 等. 基于电流优化的无速度传感器感应电机零频穿越策略[J]. 电工技术学报, 2022, 37(19): 4947-4956.

Luo Cheng, Li Ruhan, Yang Kai, et al. Current optimization-based zero frequency ride-through method for speed-sensorless induction motor drive[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4947-4956.

[17] 陈伯时. 电力拖动自动控制系统: 运动控制系统[M]. 3版. 北京: 机械工业出版社, 2003.

[18] 耿捷. 激光测距研究与设计[D]. 北京: 北方工业大学, 2016.

[19] 梁超宇. 高响应直线电机伺服系统信号检测技术的研究[D]. 武汉: 华中科技大学, 2007.

[20] 韩京清, 王伟. 非线性跟踪—微分器[J]. 系统科学与数学, 1994, 14(2): 177-183.

Han Jingqing, Wang Wei. Nonlinear tracking-differentiator[J]. Journal of Systems Science and Mathematical Sciences, 1994, 14(2): 177-183.

[21] 韩京清, 袁露林. 跟踪-微分器的离散形式[J]. 系统科学与数学, 1999, 19(3): 268-273.

Han Jingqing, Yuan Lulin. The discrete form of tracking-differentiator[J]. Journal of Systems Science and Mathematical Sciences, 1999, 19(3): 268-273.

[22] 武利强, 林浩, 韩京清. 跟踪微分器滤波性能研究[J]. 系统仿真学报, 2004, 16(4): 651-652, 670.

Wu Liqiang, Lin Hao, Han Jingqing. Study of tracking differentiator on filtering[J]. Acta Simulata Systematica Sinica, 2004, 16(4): 651-652, 670.

[23] 韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程, 2002, 9(3): 13-18.

Han Jingqing. From PID technique to active disturbances rejection control technique[J]. Control Engineering of China, 2002, 9(3): 13-18.

[24] Pu Zhiqiang, Yuan Ruyi, Yi Jianqiang, et al. A class of adaptive extended state observers for nonlinear disturbed systems[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5858-5869.

[25] 郑大钟. 线性系统理论[M]. 2版. 北京: 清华大学出版社, 2002.

[26] Gao Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference, Denver, CO, USA, 2003: 4989-4996.

Thrust Cooperative Control and Speed Measurement Algorithm of Segmented Long Primary Double-Sided Linear Induction Motor

Zhang Mingyuan1,2Shi Liming1,2Fan Manyi1,2Zhou Shijiong1,2Zhu Haibin1,2

（1. Key Laboratory of Power Electronics and Electric Drive Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100190 China 2. University of Chinese Academy of Sciences Beijing 100049 China）

Long primary double-sided induction motors (LP-DSLIM) are widely used in rail transit and linear motor based electro-magnetic launch system, with the advantages of large thrust weight ratio and small dynamics longitudinal end effect during high-speed operation. To reduce the voltage and capacity of the inverter and to improve the power factor of LP-DSLIM, the long primary is segmented into several primary segments and the power supply mode of multiple inverters is adopted. However, the thrust characterization method and high-performance cooperative control strategy of segmented LP-DSLIM powered by multiple inverters have to be studied deeply. Besides, in the field oriented control, the speed participates in the field orientation and the speed measurement accuracy will directly affect the thrust control effect. It is necessary to increase the speed measurement accuracy in motor drive. This paper proposes a thrust cooperative control strategy of segmented LP-DSLIM powered by multiple inverters and a linear speed measurement algorithm.

Firstly, the characteristics of one inverter driving a unit motor are studied basing on unit motor mathematical model of segmented LP-DSLIM. When the d axis currents of all unit motors are equal tosdand the q axis currents of all unit motors are equal tosq, the secondary flux equation and electromagnetic thrust equation of segmented LP-DSLIM powered by multiple inverters are similar to that of rotating induction motor. Whensdis a constant value, the secondary flux linkage is kept constant and the electromagnetic thrust is controlled bysq. The thrust of each unit motor is naturally proportional to the length of the coupling secondary, which realizes cooperative thrust control. Then, according to the linear motor motion equation and the thrust model, the linear extended state observer (LESO) is established to observe the speed. The speed observer is compared with the tracking differentiator (TD) speed measurement algorithm.

Simulation results and experimental results verified the effectiveness of the established speed observer and the proposed thrust cooperative control strategy. When the filter factor0in TD is small, the observed velocity noise is large and the thrust fluctuation is large. When0in TD is large, the observed velocity lags seriously and the thrust loss is large. The constructed speed observer can simultaneously meet the requirements of low noise and no lag, small speed measurement error. Meanwhile, the thrust fluctuation is small and there is less thrust loss when the observation speed of constructed speed observer is applied for field oriented control. Under the proposed control strategy, the thrust of each unit motor is proportional to the length of its coupling secondary, the total thrust is kept constant.

The following conclusions can be drawn: ①Under the proposed cooperative control strategy, the secondary flux equation and electromagnetic thrust equation of segmented LP-DSLIM powered by multiple inverters are similar to that of rotating induction motor. The thrust of each unit motor is naturally proportional to the length of the coupling secondary. The cooperative control strategy is suitable to electromagnetic thrust system. ②The low noise and small lag of TD velocity measurement algorithm cannot be obtained simultaneously, which will lead to large thrust noise or thrust loss in the field oriented control. The speed measurement algorithm of the constructed speed observer is simple with low noise and no lag. When the constructed speed observer is used for field orientation, the thrust fluctuation is small, the thrust loss is small, and the control effect is better than that of the TD speed measurement algorithm.

Long primary double-sided linear induction motor, multiple inverters drive, cooperative thrust control, speed measurement algorithm, linear extended state observer

10.19595/j.cnki.1000-6753.tces.211230

TM359.4

国家重点研发计划资助项目（2016YFB1200602-19）。

2021-08-09

2021-10-09

张明远 男，1995年生，博士研究生，研究方向为大功率电力电子变换技术与直线电机驱动控制。E-mail：myzhang@mail.iee.ac.cn

史黎明 男，1964年生，研究员，博士生导师，研究方向为特种电机和驱动控制、磁悬浮技术、电能无线传输技术。E-mail：limings@mail.iee.ac.cn（通信作者）

（编辑 赫蕾）