扁钢管混凝土柱框架的抗侧抗震性能研究

陈 嵘，朱云祥，郁家麟，黄世晅，姚红伟，黄宏盛

(1.国网浙江省电力有限公司,浙江 杭州 310003；2.国网浙江省电力有限公司 嘉兴供电公司，浙江 嘉兴 314033)

就目前土木工程的发展现状而言，工程结构呈现出向大跨、高耸方向的发展趋势；而钢管混凝土因其具有应对恶劣极端的建造环境和满足现代施工技术的施工要求的优势，在高层建筑、桥梁工程和隧道工程中获得了广泛的应用[1-6]。方形截面钢管混凝土相比于圆形截面钢管混凝土而言，在梁柱节点施工时更加方便，因此在实际工程中应用更加广泛[7-8]。但是，当框架柱采用方形截面钢管混凝土形式时，面临墙体包围不能柱体且沿墙体方向上的柱面更加突出的问题，很大程度影响了室内布置的美观；扁钢管混凝土柱作为框架柱时，可以做到不突出墙体，具有更广阔的应用前景[9]。由于扁钢管混凝土的抗侧刚度在弱轴方向较小导致扁钢管混凝土框架结构在此方向的抗侧刚度也偏小，使得结构抗侧性能及抗震性能较低。因此，为了进一步提高扁钢管混凝土框架结构的应用价值，研究扁钢管混凝土框架结构的抗侧性能及抗震性能是必要的。

1 有限元模型

1.1 材料本构

1.1.1混凝土的本构关系

图1为约束混凝土的应力-应变曲线，分为上升段OA、水平段AB及下降段BC，采用文献[10]中的应力-应变关系式。根据《混凝土结构设计规范》(GB 50936—2014)得到混凝土单轴拉压应力-应变关系。

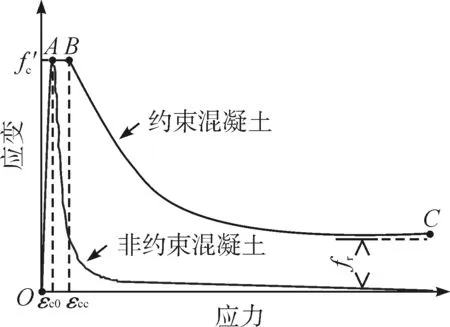
图1 混凝土单轴受压的应力应变曲线Fig.1 Stress-strain curve of concrete under uniaxial compression

1.1.2钢材的本构关系

图2为钢材的应力-应变曲线，应力-应变关系分为4段，采用文献[11]中的应力-应变表达式。

图2 钢材的应力应变曲线Fig.2 Stress-strain curve of steel

1.2 模型建立

采用C3D8R实体单元建立混凝土，采用S4R壳单元建立钢管、钢梁，采用R3D4刚体单元建立刚性加载板，该模型可以在减小计算量的同时较准确地模拟钢梁可能发生的屈曲变形；有限元模型如图3所示。

图3 有限元模型Fig.3 Finite element model

采用硬接触的形式模拟钢管与混凝土法向接触状态，同时在切向引入库伦摩擦。采用绑定连接的形式模拟顶部刚性加载板与钢管的接触状态；而顶部刚性加载板与混凝土则采用硬接触的形式。梁柱节点采用耦合连接。钢管混凝土底部约束所有自由度，完全固定。在柱顶建立参考点，与刚性加载板耦合，轴压载荷状态通过对参考点施加竖向集中力进行模拟，水平荷载通过在左柱顶通过施加水平位移进行模拟。

1.3 有限元模型的验证

文献[12]中的矩形钢管混凝土柱试件的有限元模型采用本文的建模方法建立，同时结合试验结果进一步验证有效性。表1为钢管混凝土柱的试件尺寸和材料性能相关各项参数，其中B为矩形截面的宽度；H为其高度；t为钢管厚度；L为柱高；fy为钢材屈服强度；fcu为混凝土立方体抗压强度标准值。

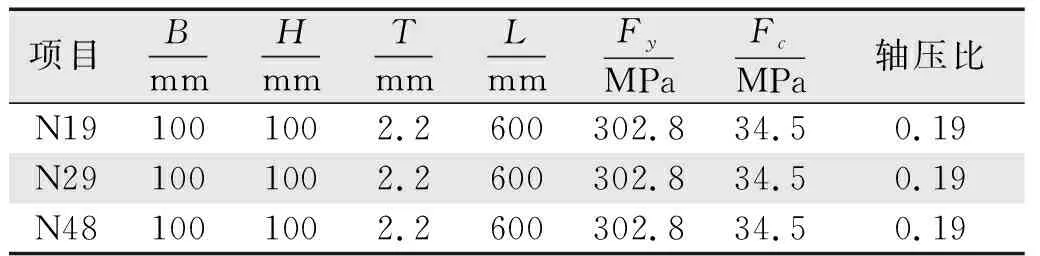
表1 试件参数 Tab.1 Specimen parameters

图4为有限元模拟与实际试验所获得的荷载-侧移曲线。

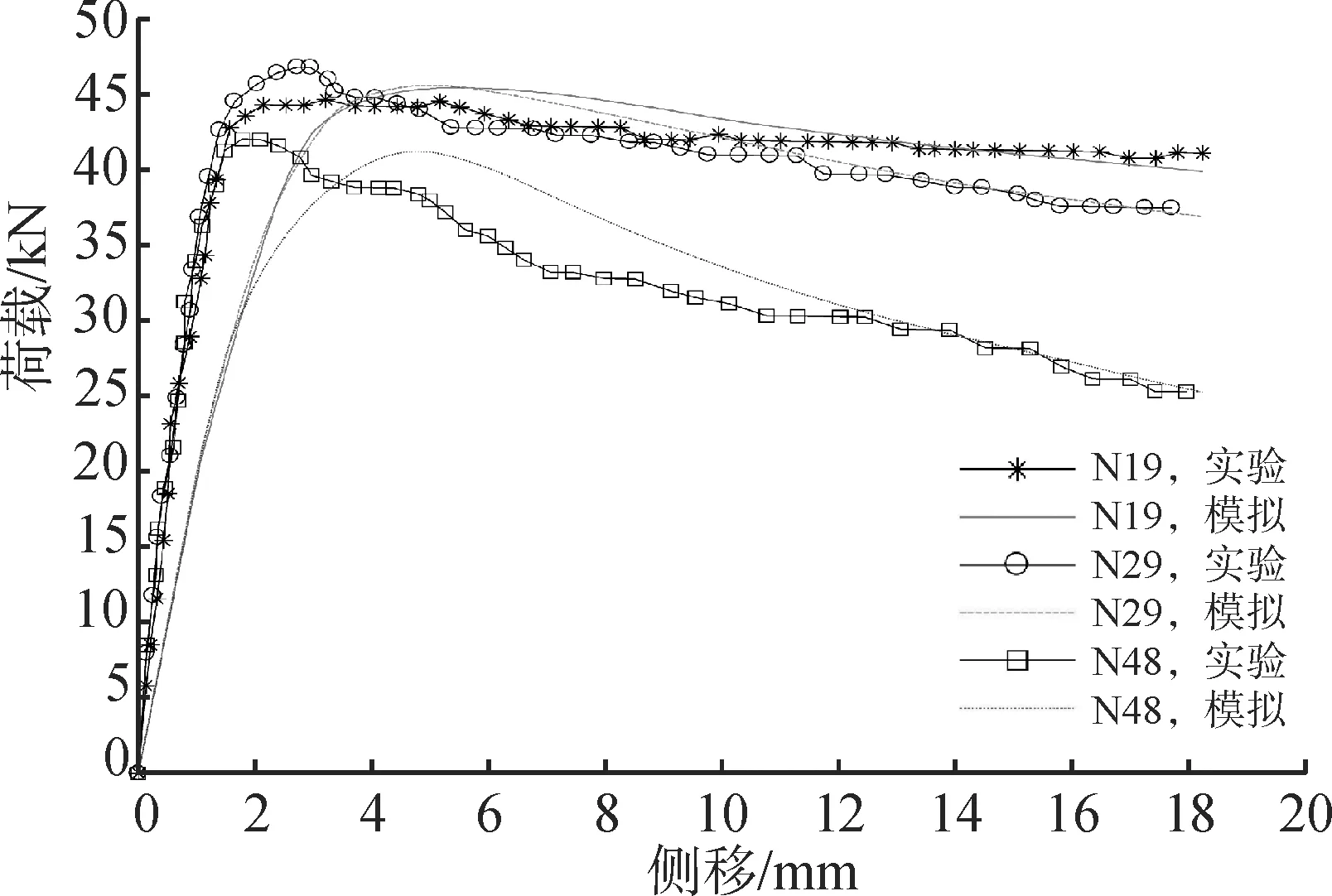
图4 荷载-侧移曲线对比Fig.4 Comparison of load-side displacement curves

从图4可以看出，各试件的有限元模拟结果与试验结果差异较小；这表明本有限元建模方法的有效性，最后可依据其进行后续分析计算。

2 扁钢管混凝土框架抗侧性能参数分析

表2为有限元模型的具体参数。其中，KJ表示扁柱框架结构，第1个数字表示截面宽高比(宽高比依次为1、2、3.75)，第2个数字表示轴压比(轴压比依次为0.3、0.4、0.5)。KJ13、KJ23和KJ33其保证轴压比均在0.3的水平下研究截面宽高比对扁钢管混凝土框架抗侧性能的影响。梁的截面尺寸为H400 mm×150 mm×8 mm×12 mm，梁长为2 900 mm。KJ33、KJ34和KJ35在保证截面宽高比均在3.75的水平下，研究轴压比对扁钢管混凝土框架抗侧性能的影响。试件KJp33为采用内隔板式增强，在保证钢材截面面积相同的前提下，钢管厚度取为10 mm，KJ33和KJp33则用以研究截面增强形式对扁钢管混凝土框架抗侧性能的影响。

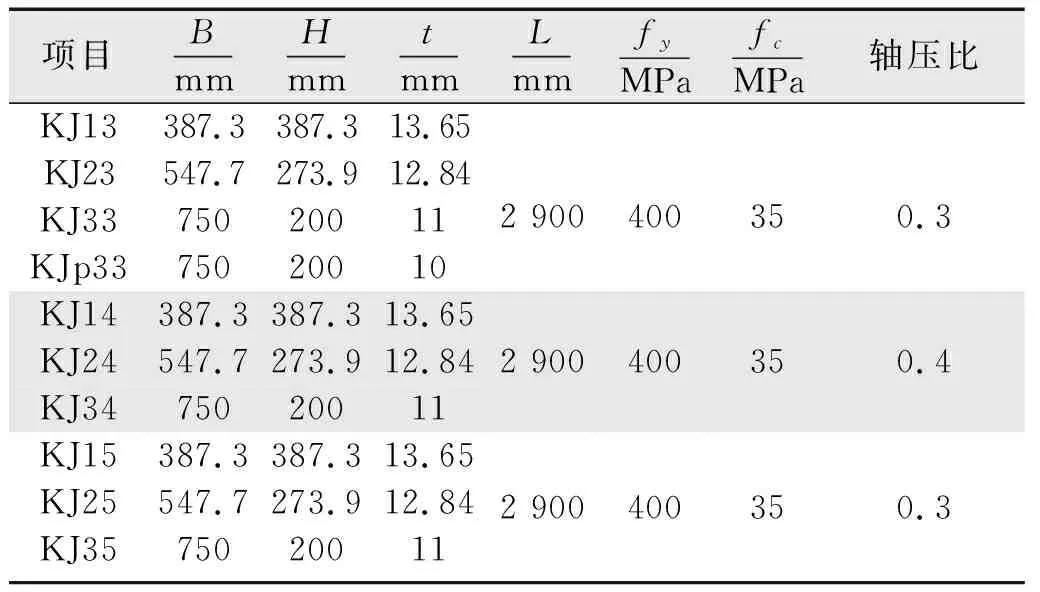
表2 框架结构模型参数Tab.2 Parameters of frame structure model

2.1 轴压比的影响

各试件在不同截面宽高比和轴压比下的荷载-位移情况，结果如图5所示。图5(a)、(b)、(c)分别表示在宽高比分别为1、2、3.75的情况下，各试件在轴压比0.3、0.4、0.5梯度下的荷载-位移曲线。

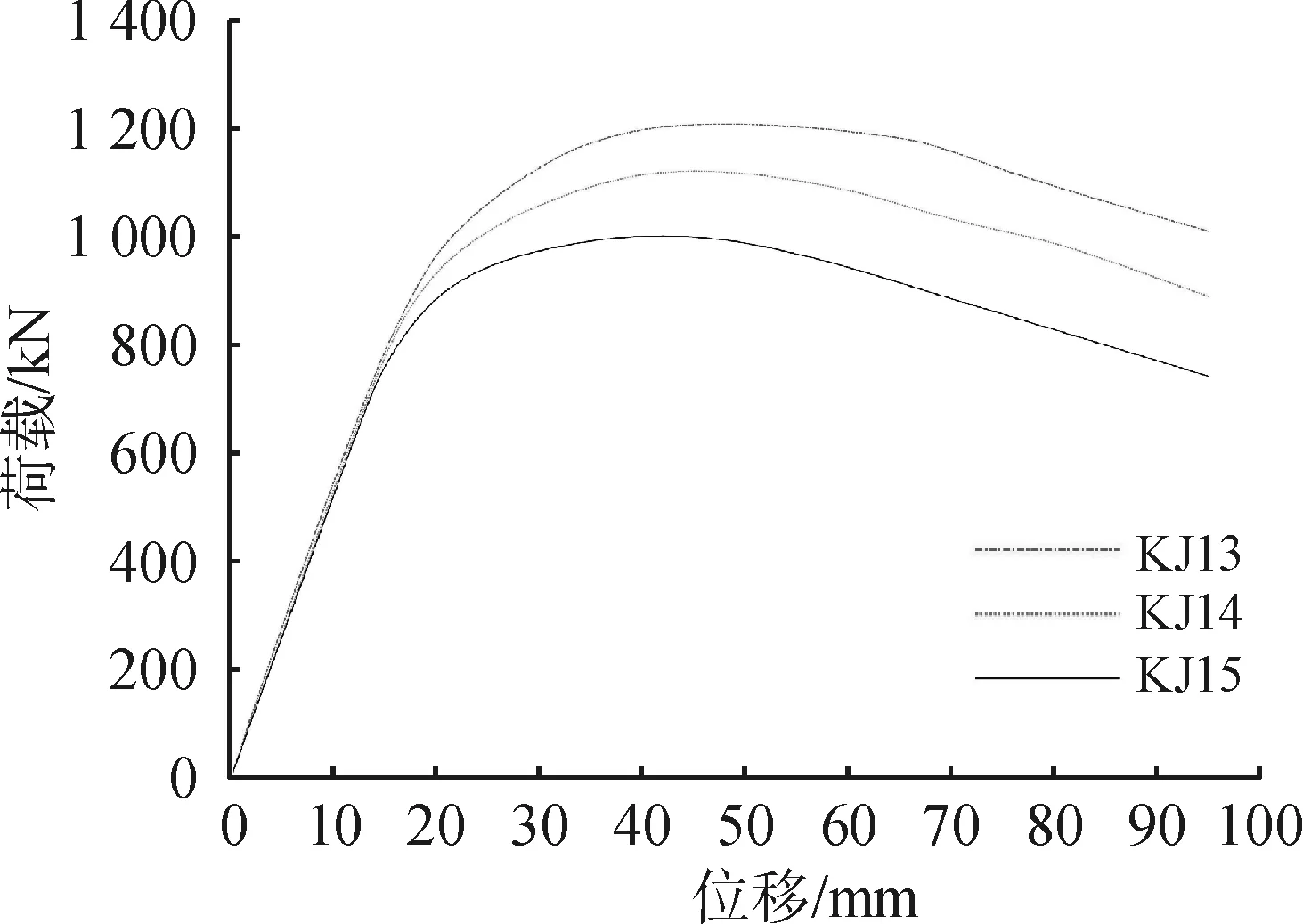
(a)宽高比1

图6为峰值荷载随轴压比的变化情况；图7为峰值荷载对应的位移随轴压比的变化情况。

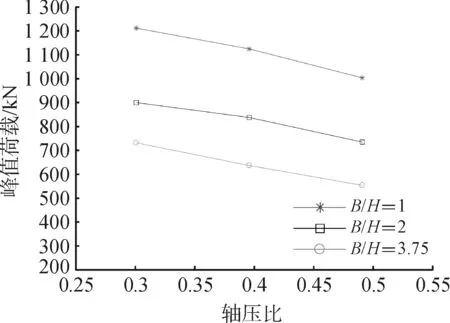
图6 轴压比对峰值荷载的影响Fig.6 Effect of axial compression ratio on peak load

图7 轴压比对峰值荷载的位移的影响Fig.7 Effect of axial compression ratio on displacement at peak load

从图6可以看出，随着轴压比增大，峰值荷载呈现近似线性减小的趋势。当截面宽高比为1的方柱试件，在轴压比分别为0.4和0.5时，相对于轴压比为0.3的，峰值荷载分别下降了7.2%和17.3%；当截面宽高比增加到2时，峰值荷载下降幅度分别为7.0%和18.5%；当截面宽高比增至3.75时，峰值荷载进一步下降，下降幅度分别为13.1%和24.6%；且峰值荷载在轴压比分别为0.3和0.4时下降水平相近。但当轴压比为0.5时，呈现出明显下降趋势。究其原因，可能为轴压在柱长方向产生的附加弯矩会随着加载位移的增大进一步加快抗侧力的降低进程，因此结构的峰值荷载会随着轴压的增大而减小。

同样的，从图7可以看出，峰值荷载对应的位移也会出现相同的变化趋势。截面宽高比为1的方柱试件的峰值荷载对应位移下降了8.9%和13.9%；宽高比为3.75的试件在轴压比分别为0.4和0.5时，下降了27.3%和36.9%。

2.2 宽高比的影响

图8为荷载位移曲线的峰值荷载随截面宽高比的变化情况；图9为峰值荷载对应的位移随截面宽高比的变化情况。

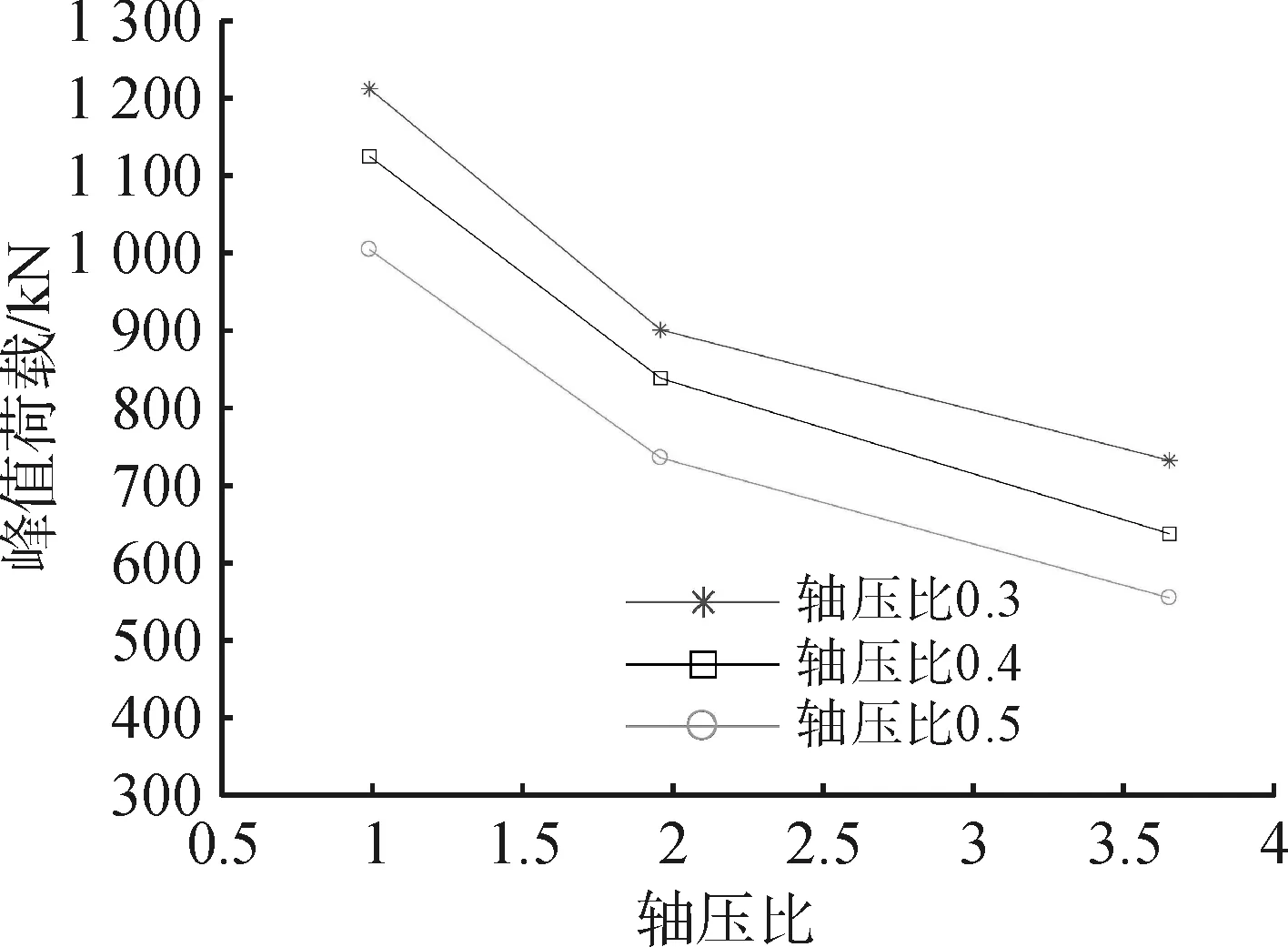
图8 宽高比对峰值荷载的影响Fig.8 Effect of aspect ratio on peak load

从图8可以看出，在相同轴压比下，结构的峰值荷载随着宽高比的下降而降低，且在不同轴压比条件下峰值荷载的下降水平基本相同。当轴压比为0.3时，扁柱试件KJ23、KJ33的峰值荷载较方柱试件KJ13分别下降25.9%和39.9%；当轴压比为0.4时，峰值荷载下降幅度分别为25.7%和43.6%；当轴压比为0.5时，峰值荷载下降幅度分别为27.0%和45.2%。这表明截面宽高比对峰值荷载的影响大于轴压比。

从图9可以看出，峰值荷载对应的位移随截面宽高比无明显变化规律。

图9 宽高比对峰值荷载的位移的影响Fig.9 Effect of aspect ratio on displacement of peak load

2.3 截面横隔板的影响

图10为试件KJ33和试件KJp33的荷载-位移曲线的对比结果。在宽高比特别大的扁柱截面中焊接横隔板，以增强长边钢板对混凝土的约束作用，进一步探究增强措施对结构抗侧性能的影响。

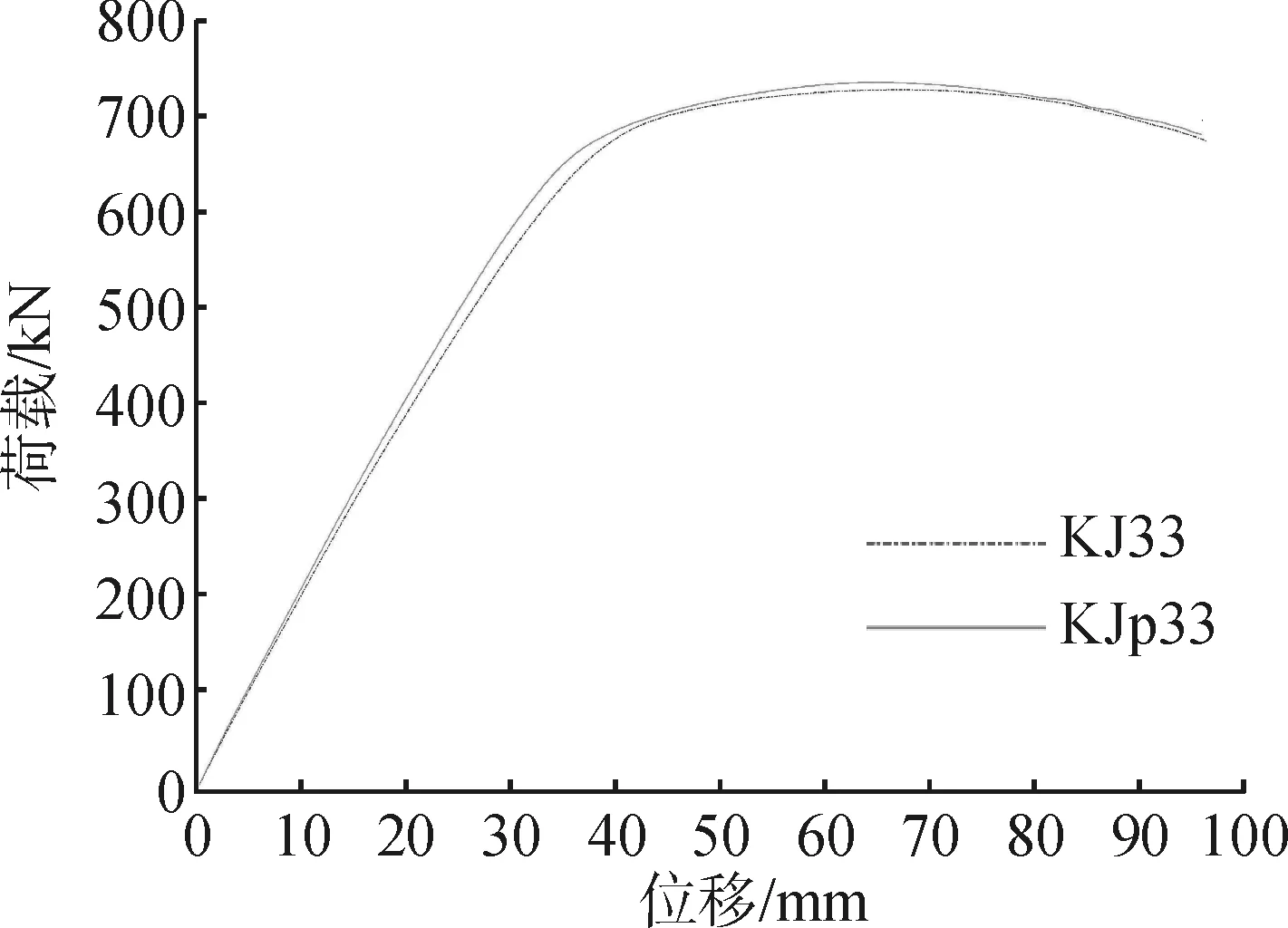
图10 横隔板对荷载-位移曲线的影响Fig.10 Effect of diaphragm on load-displacement curve

从图10可以看出，框架荷载-位移曲线在截面加横隔板的情况下并无明显变化。究其原因：(1)加横隔板虽然可以提高钢管对混凝土的约束作用，但其提升作用幅度远小于已有钢管与混凝土的抗侧贡献；(2)在保持钢管截面面积相等的情况下，普通矩形截面钢管沿中性轴方向的截面惯性矩相比于加内隔板截面要大，因此在截面抗弯刚度层面弥补了钢管对混凝土的约束不足的弱点。

3 扁钢管混凝土框架支撑结构的滞回性能

拟采用增设钢支撑的方式提高结构整体的抗侧刚度，从而达到增强扁钢管混凝土柱沿弱轴方向的抗侧刚度的目的。为此设计了如表3所示的有限元结构模型分析钢支撑对加隔板式扁柱框架结构滞回性能的影响。其中，KJ为扁柱框架结构；KJZ为扁柱框架中心支撑结构；Lb表示梁长。

表3 框架支撑结构体系的参数Tab.3 Parameters of frame support structure system

图11为KJ模型及KJZ模型示意图。中心支撑为矩形钢管截面，两端与梁柱连接处采用三角形节点板，并采用方形封头板进行密封处理。其中封头板与中心支撑、三角节点板与封头板、三角节点板与钢管混凝土柱的钢管面和梁的下翼缘均采用绑定连接。

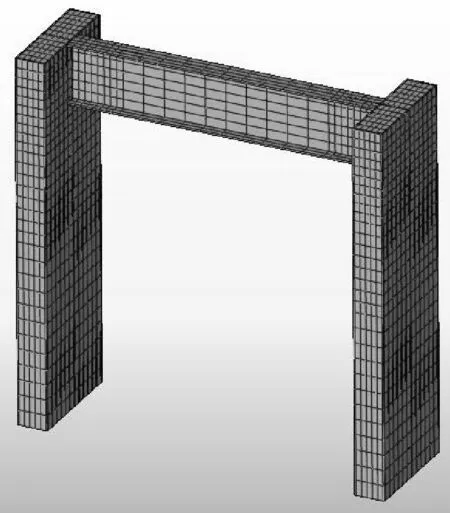
(a)框架结构KJ (b)框架支撑结构KJZ

有限元模型采用位移加载制度，按照10、20、30 mm的梯度依次进行加载，每级位移循环1次；将从滞回曲线、骨架曲线、刚度变化、延性及耗能5个方面对扁钢管混凝土框架支撑结构的抗震性能进行分析。

3.1 滞回曲线

图12为有限元模型计算得到结构KJ与结构KJZ的滞回曲线。结果表明结构KJ和结构KJZ的滞回环呈现正反对称状态且保持较为饱满的形状，这表示2种结构均具有一定的塑性变形能力和耗能能力。通过进一步比较KJZ框架支撑结构体系与KJ框架受力体系，发现框架支撑结构KJZ具有更大的滞回环面积与抗侧刚度，结构的耗能能力更强。

(a)框架结构KJ

3.2 骨架曲线

图13为有限元模型计算得到的结构骨架曲线[13-14]。

图13 骨架曲线Fig.13 Skeleton curve

从图13可以看出，在加载初期随着位移的增加，荷载会逐渐增大，直至达峰值荷载，而后表现降低的变化趋势。此外，在水平往复荷载作用下，增设支撑可以增强结构的抗侧性能，结构KJZ结构的抗侧刚度得到了提升，骨架曲线的峰值荷载相较于无支撑的KJ模型也提高了10.8%。

采用割线刚度来参数化分析结构抗侧刚度的变化情况，割线刚度ki按式(1)计算：

(1)

式中：+Fi、-Fi分别表示第i次正、反向峰值点的荷载值； +Xi、-Xi分别表示第i次正、反向峰值点的位移值。

图14表示割线刚度在各级循环加载条件下的变化情况[15-17]。

图14 割线刚度变化Fig.14 Secant stiffness change

从图14可以看出，KJ模型及KJZ模型刚度随着加载级数增加均呈降低趋势。相比于结构KJ，结构KJZ的割线刚度在初期加载循环中下降幅度较大；而在加载级数较大时，2种结构的割线刚度保持在相近水平。虽然增设支撑提高了结构刚度，但是在加载过程中刚度下降幅度也很明显，这是因在加载位移较大时，钢支撑会发生屈服情况，导致较大变形的产生所致。因此，增设支撑对结构抗侧力的提升作用是有限的，结构加载位移较大时变形也可以较为自由地开展，在后期2种结构的割线刚度无明显差别。

3.3 延性分析

结构的延性特征采用位移延性系数来定量分析[18-20]，位移延性系数μ应按式(2)求得：

(2)

式中：Δu表示结构的极限变形，取下降阶段85%峰值荷载所对应的位移值；Δy表示结构的屈服变形，本文根据能量法确定。

表4为框架结构KJ和框架支撑结构KJZ的屈服位移Δy、极限变形位移Δu和延性系数计算结果。

表4 结构的延性系数Tab.4 Ductility coefficient of structure

由表4可知，增设支撑结构对结构的延性有显著的提升作用，结构的延性系数相比于框架结构提高了38.2%。

3.4 耗能分析

图15为能量耗散系数[5]随加载级数的变化情况，结构表现出相同的整体变化趋势。

图15 能量耗散系数Fig.15 Energy dissipation coefficient

图16为单级(累积)耗能随加载级数的变化情况，图16中的4条曲线分别给出2个结构的单级和累积耗能百分比随加载级数变化情况；结果表明，结构的单级耗能百分比随着加载级数近似线性增加。

图16 单级/累积耗能百分比Fig.16 Percentage of single-stage/accumulated energy consumption

4 结语

(1)本设计基于ABAQUS数值模拟，分析了轴压比、截面宽高比和截面横隔板对扁钢管混凝土柱框架结构的抗侧性能的影响。结果表明：结构的峰值荷载随着轴压比增大而减小；峰值荷载与宽高比的关系也保持相似变化趋势；

(2)通过数值模拟和参数分析可知，轴压比和宽高比对结构峰值荷载所对应的位移无明显影响。此外，增设横隔板对结构性能无明显提升作用，截面增强对结构抗侧性能也无明显提升作用；

(2)通过对扁柱框架支撑结构在水平往复加载情况下进行有限元模拟，结果表明：增设支撑可以增强结构的耗能能力。骨架曲线的峰值荷载与试件的割线刚度在此情况下均得到提升，进一步增加了滞回耗能面积；

(3)参数分析结果表明，增设支撑结构对结构的延性有显著的提升作用；结构的延性系数相较于框架结构提高了38.2%，在工程实践中可优选选用增设支撑的形式提高结构的抗震性能。