基于阶次提取的车用电机振动快速计算方法

杨驰杰 钱平 陈寒霜 田子龙 任超

广州汽车集团股份有限公司汽车工程研究院 广东省广州市 511434

1 引言

驱动电机的振动噪声水平是衡量整车舒适性的重要指标，也是电动汽车振动噪声性能控制的重难点之一。研究电磁振动计算可以改进电机设计方法，是解决电机电磁振动与噪声问题的一项关键内容[1,2]。电机电磁振动主要包含电磁仿真和结构仿真两方面内容，电磁仿真是通过电磁参数建立电磁有限元模型，从而计算出引发电机壳体振动的电磁激励[3-5]。结构仿真是以电机定子齿面电磁激励施，计算电机壳体表面法向的振动响应[6]。

目前电动乘用车驱动电机大多采用永磁同步电机[7]，其工作转速通常为0～12000r/min，若要分析电机电磁振动在全转速段的情况，则需要进行几百个转速工况才能获得较好的转速分辨率，计算量非常大，较为耗时和占用大量计算资源。本文通过阶次提取技术将时域的非平稳电磁激励转换为频域及角度域的电磁激励，将稳态电磁激励施加到电机有限元模型中进行电机壳体表面法向振动响应求解，缩减了仿真时间和计算资源，仿真效率大大提升。

2 磁密计算及电磁力阶次提取

2.1 气隙磁密仿真计算

在计算电机气隙磁密之前，需要先确定电机运转时的外特性。电机外特性主要分为恒转矩区和恒功率区两部分。对于全油门加速情形，当车速较低时，电机处于恒转矩区运转，车辆具有良好的起步加速性能；当车速增加到一定程度，电机进入恒功率区运转，此时转矩与转速的乘积为定值，表征了车辆最高车速等。这种控制标定策略可使车辆具有较强动力性能，但是会最大程度地激发出电机的阶次振动及噪声，因此工程上常采用电机满载外特性作为评价车用驱动电机振动噪声性能的重要工况。

本文针对某车用永磁同步电机的满载外特性中电机在不同转速时振动进行分析，该电机极数为8 极，定子槽数为48 槽，满载外特性曲线如图1 所示，图中电机转速n0=4500r/min 所对应的点N 为电机外特性曲线转矩输出拐点（该拐点表示恒转矩区终止、恒功率区起始），Tqmax表示电机最大输出扭矩。

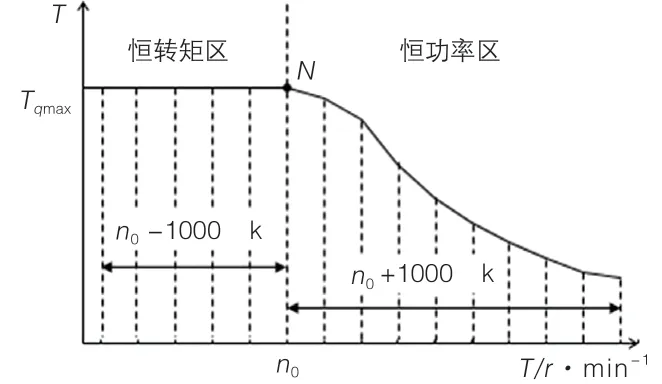
图1 电机外特性曲线

本文采用Maxwell 软件进行二维非线性瞬态电磁场分析。针对图1 所示电机满载外特性曲线，以电机外特性曲线转矩输出拐点转速n0为基点，1000rpm 的转速间隔在0～12000r/min 转速区间内取12个不同转速（即转速n=n0±1000k，其中k为正整数，即n=500，1500，2500、3500，4500、5500、6500、7500、8500、9500、10500、11500），计算所得气隙磁密既包含时间项又包含空间项，是个时空二维集合，在分析时可同时得到某一时刻电机中沿气隙周向分布的磁密和气隙中某一位置随着不同时间变化的磁密，表1、表2 分别显示了电机以4500r/min 转速运转时0～2°空间角度内节点0～0.12ms时间段内的气隙磁密，其中表1 为径向磁密，表2 为切向磁密。

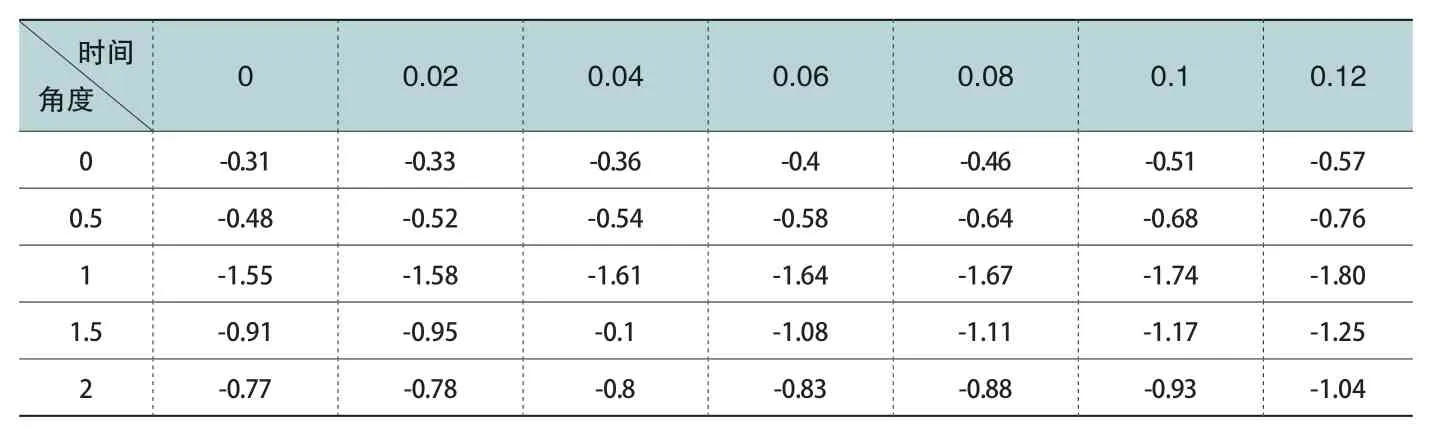
表1 径向磁密时间历程及空间分布

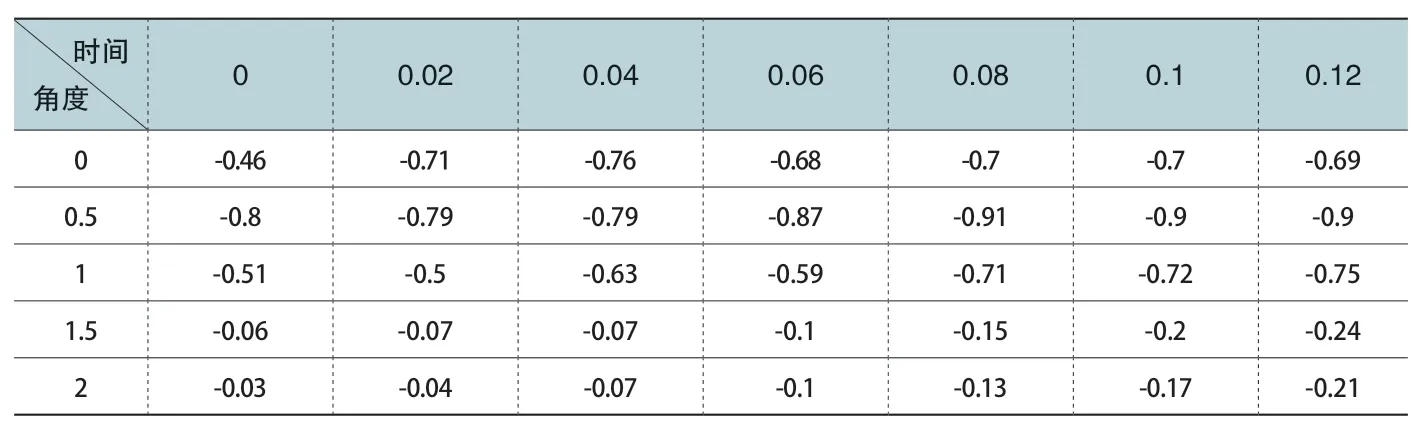
表2 切向磁密时间历程及空间分布

2.2 电磁力计算及阶次提取

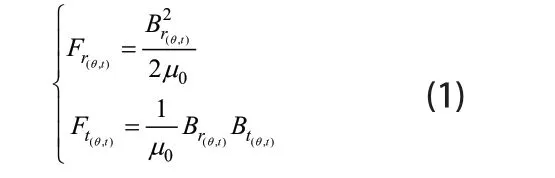
计算所得力密度函数均是空间角θ与时间t的二维函数，设某个角度θk位置电磁力密度时间历程为，对其进行离散傅立叶变换：

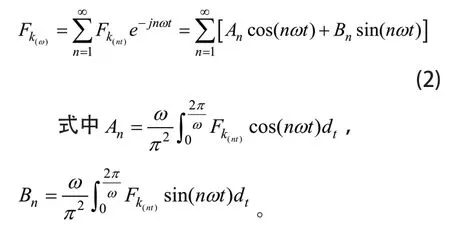
通过数值计算，求解电磁力的阶次、频率及力波幅值等参数。

3 电机结构振动响应计算

3.1 电机结构建模

由于本文主要研究通过阶次提取的方法实现电机全转速段电磁振动响应快速计算的有效性及提升效率，而非研究电机结构的准确建模方法，不再着重研究电机定子铁芯及绕组的等效，采用铁芯叠片结构视为叠片平面各向同性材料等成熟工程经验[8]进行建模，具体如下：1)采用实体等效定子铁芯叠层结构，将叠片平面（x-y 平面）视为各向同性材料，与叠片平面正交的轴向（z 向）刚度不同；2)采用直导体等效定子槽内多匝线圈，各部件材料参数如表3 所示，硅钢片弹性模量Ec=200GPa，硅钢片剪切模量Gc=75GPa,电机整机有限元模型如图2 所示，图中三角形表示电机仿真模型施加边界条件。

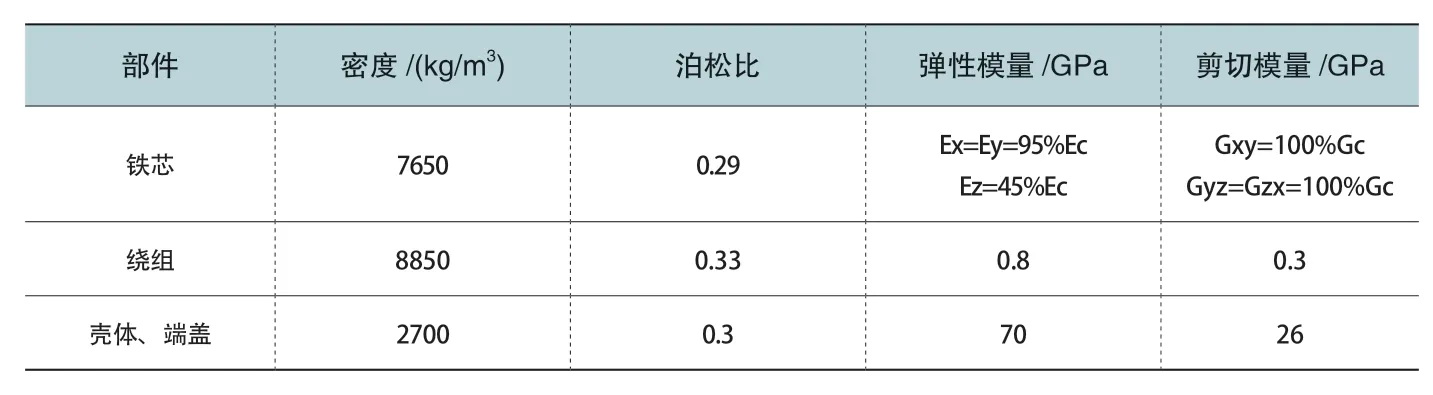
表3 有限元模型材料参数

图2 电机整机有限元模型

3.2 电磁力加载

电磁振动谐响应计算需要将频域电磁激励加载到电机有限元模型上，第1 节已获得二维平面内定转子气隙间电磁力阶次力，忽略电机电磁力在轴线方向的不均匀分布，将第1 节所得的不同阶次、频率的电磁力加载到定子铁心齿面，加载公式如下

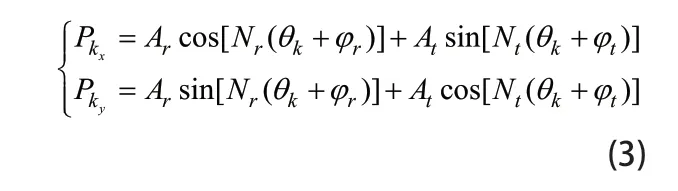
图3 电磁力加载形式

4 快速计算方法的误差及效率

本文取电机壳体表面任意一节点法向振动响应为目标，对全转速段电机壳体振动快速计算方法的精度进行评价。将采用快速算法计算的电机壳体振动响应差值定义为ΔV=V-V′，误差定义为Δ=(V-V′)/V×100%，其中V表示采用快速算法计算的节点法向振动响应的均方根值，V′表示直接采用有限元仿真计算电磁力获得的节点法向振动响应的均方根值振动响应。表4 给出了在全转速段内任取的9 个转速工况对应的振动响应误差，可以看出：9 个转速工况的误差均很小，在3%以内。本文基于阶次提取的快速计算方法的误差相对于电驱系统振动噪声仿真计算来说是一个相对小量，具有较高的置信度，可以进行工程化应用。

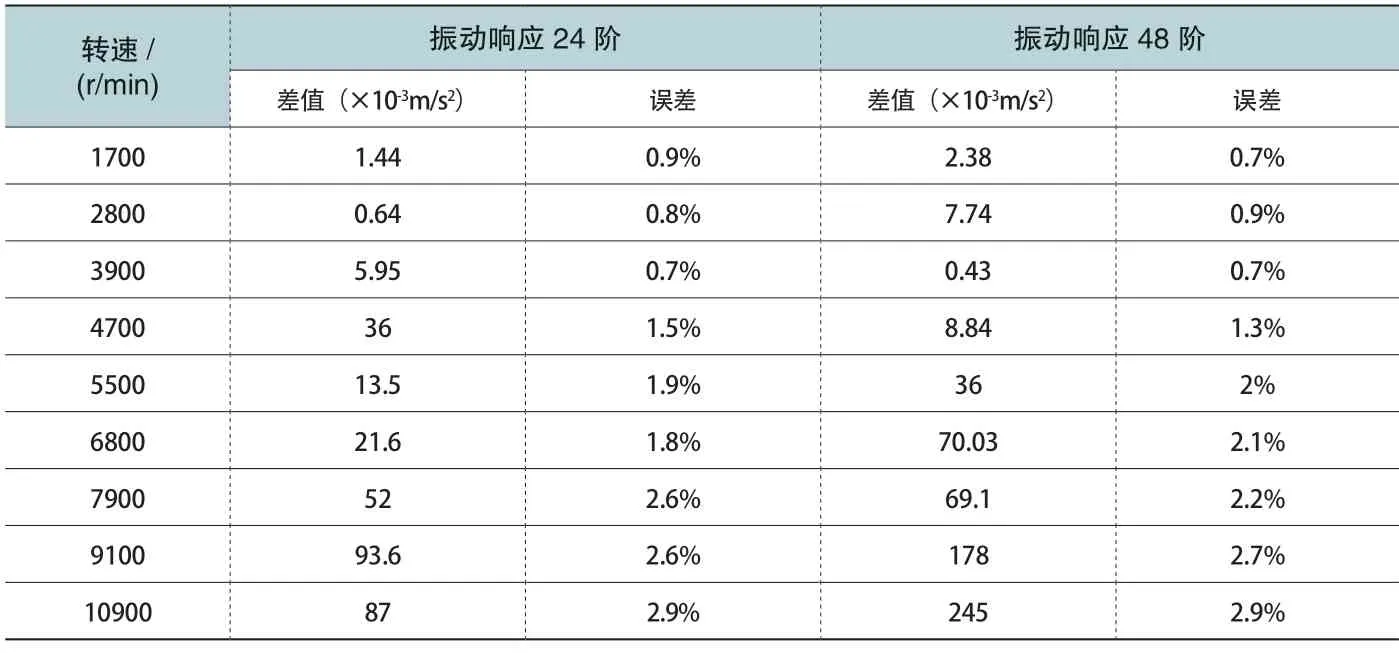
表4 法向振动响应误差

对于电机全转速区间内的振动分析，传统方法通常需要计算足够多转速工况的计算才能获得具有较高转速分辨率的振动响应变化，本文提出的方法在效率提升方面具有明显优势。若对0～12000r/min 转速区间进行全转速段振动响应分析，设转速分辨率为 Δn（即每隔 Δn计算一个转速工况），采用传统方法逐个转速工况求解电磁力，则需要进行12000/ Δn个工况计算，采用本文提出的阶次提取方法只需要进行12 个转速工况计算，效率提升为：

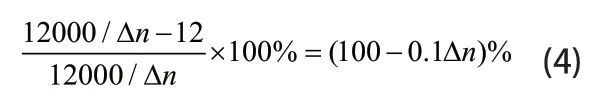
当转速分辨率取200r/min,即Δn=200，此时相比较传统方法，本文快速计算方法效率提升了80%，当转速分辨率 Δn进一步缩小时，本文快速仿真方法对效率的提升效果会进一步增大。

5 结语

本文基于多物理场耦合仿真计算，通过阶次分析技术将时域的非平稳信号转换为角度域及频域的电磁激励，实现车用驱动电机电磁振动的快速计算。研究内容总结如下：

（1）本文提出的快速计算方法在全转速段内任取的9 个转速工况的误差均很小，都在3%以内，置信度较高，可以进行工程应用；

（2）对于电机常用转速区间内壳体振动响应分析，本文基于阶次提取的的快速计算方法在误差允许范围内，可以较大程度提升效率，当需要分析转速间隔越小，快速计算方法的效率提升也越大。