车辆半主动悬架减振支柱的刚度特性分析

黄大星

韶关学院 智能工程学院 广东省韶关市 512005

汽车悬架结构关系到汽车平顺性能，随着我国车辆保有量的增加，车辆使用者对车辆的舒适性、操纵性、稳定性和可靠性的要求日益提高。为了提高车辆使用性能，车辆设计者们努力不断，加之电子技术以及传感器技术的快速发展，为电控悬架的产业化提供了保障，汽车悬架系统控制技术的研发不断受到动力学及其控制领域的关注。本文通过对电控减振支柱组成结构分析，推导了一种新型减振支柱关键部件——双气室空气弹簧的数学模型，对进行仿真分析。

1 新型减振支柱的结构组成

汽车独立悬架主要使用的类型有横臂式独立悬架、纵臂式独立悬架，车轮沿主销移动式悬架和多杆式悬架，其中车轮沿主销移动式悬架主要是烛式悬架和麦弗逊式悬架。麦弗逊式悬架普通运用于汽车的前独立悬架，其减振支柱是内外嵌套式结构，主要组成构件为螺旋弹簧和液压减振器。为了提高乘用车平顺性，本文在原有的前、后悬架减振支柱结构的基础上，将单向筒液力减振器与空气弹簧进行同轴一体式设计，结构如图1 所示。

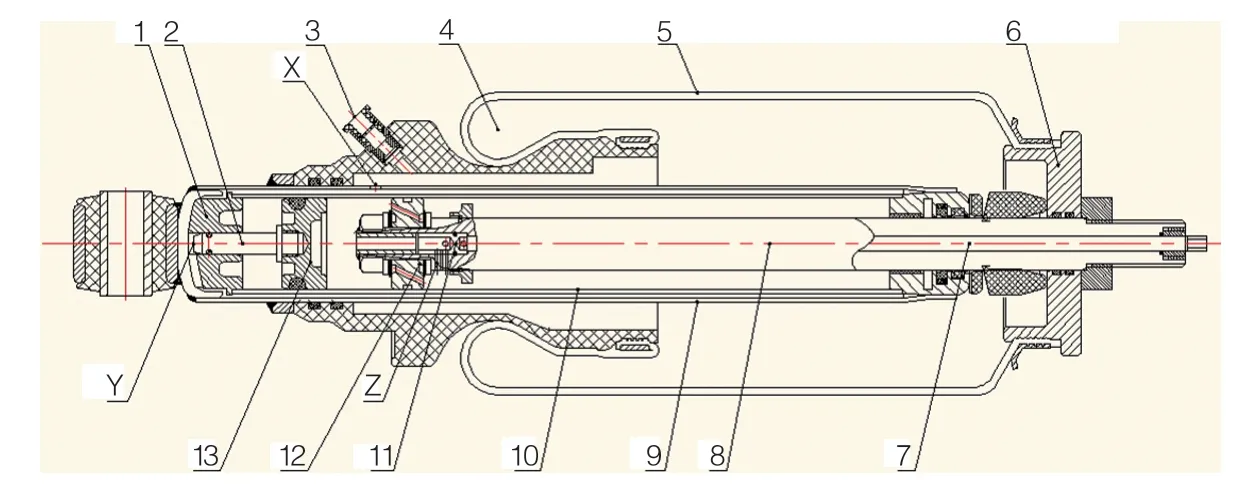
图1 新型减振支柱的结构组成

同轴一体式减振支柱结构组成是由支承座1、浮动活塞13 与油缸筒10 形成一个浮动气室，减振支柱中主气室的组成主要由上密封板6、橡胶气囊5 和气囊4 本体构成，这时外筒9 充当空气弹簧的活塞。

由振动原理可知，汽车行驶到不平路面时（或左右轮胎气压不一致时），车辆悬架中减振器受到外界压力（当压缩行程时）或爱以到外界拉伸（当伸张行程时），减振器活塞向上或向下移动，导致作用在空气弹簧上的载荷发生了变化，空气弹簧的刚度特性也随之发生变化，这时减振器体现出的阻尼特性就会直接影响到减振支柱压缩作用力与复原作用力的比值。由于汽车悬架行程变化的动力学特性十分复杂，主要包括非线性、外界干扰、控制时滞等复杂特性，本文所设计的新型减振支柱结构可以通过浮动活塞13 形成动力学耦合联动的关系，将汽车行驶导致悬架行程变化的复杂特性，通过浮动活塞13 的纵向运动来优化调节，以实现悬架空气弹簧的弹性缓冲与减振器的振动衰减的平衡。

2 双气室空气弹簧的数学模型

运用流体力学中节流孔气体“质量流量”模型理论，结合热力学理论中变质量开口绝热方程，这时可得双气室空气弹簧的流经孔口的气体“质量流量”数学模型[1][2][3]：

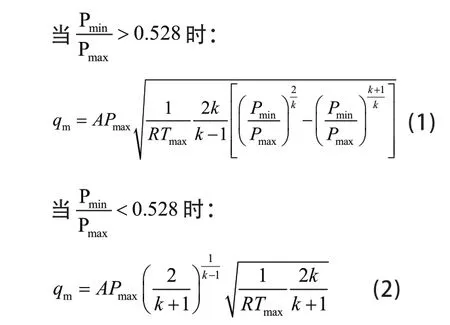
式中：Pmax=max {P1,P2}，Pa；Pmin=min {P1,P2}，Pa；Tmax——压力较大气室气体的温度，K；A——节流口的有效流通面积，m2，把节流口的有效流通面积与节流口的实际面积A0关系表示为A0=εA，ε称作收缩系数，ε取值范围在0.6～0.9之间[4]。P1——主气室内气体的绝对压力，Pa；P2——浮动气室内气体的绝对压力，Pa；

为了简化运算，提出以下三个条件假设：（1）假定汽车悬架工作条件为常压；（2）假定汽车悬架工作条件为常温；（3）假定悬架中的空气视作理想气体[4]。这时车辆半主动悬架减振支柱可看作变质量开口系统，当此系统处于绝热过程时，其方程可近似表示为：

式中：P——气体绝对压力，Pa；V——气体容积，m3；m——气体质量，kg；k——绝热指数，基于上述三种条件假设，这时k值取1.4。

车辆半主动悬架减振支柱中空气弹簧主气室与浮动气室内气体的的“质量流量”方程可表示为：

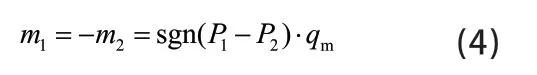
综上，减振支柱双气室空气弹簧的数学模型可表示为[5][6]：

3 车辆半主动悬架减震支柱刚度特性的仿真模型与仿真分析

3.1 车辆半主动悬架减震支柱刚度特性的仿真建模

为了明确一体式悬架减震支柱刚度特性，运用MATLAB/Simulink仿真软件对其建立仿真模型，如图2 所示。

图2 减振支柱刚度特性的Simulink 模型图

半主动悬架减振支柱模型所使用的参数如表1。

表1 半主动悬架减振支柱的仿真参数

3.2 车辆半主动悬架减震支柱特性的仿真分析

3.2.1 刚度特性的仿真分析

利用MATLAB/Simulink 仿真模型，将表2 相关性能参数代入，仿真模型的初始充气压力设定为0.4MPa、0.5MPa、0.6MPa 三种情况，对半主动悬架前、后新型一体式减振支柱总成刚度与行程的关系进行分析，仿真结果如图3 和图4 所示。图3 是前减振支柱与行程的关系曲线图，由图形曲线可得，当行程为-20mm 时，呈现阶跃。空气弹簧主气室的初始气压为0.56MPa，半主动悬架处于静平衡状态。半主动悬架前减振支柱刚度值约为10N/mm 时，半主动悬架位移处于零点位置。图4 是后减振支柱与行程的关系曲线图，由图形曲线可得，当行程为-20mm 时，呈现阶跃。空气弹簧主气室的初始气压为0.46MPa，半主动悬架处于静平衡状态。半主动悬架后减振支柱刚度值约为12.5 N/mm 时，半主动悬架位移处于零点位置。综上，认为本文所设计的半主动悬架减振支柱刚度的基本满足要求。

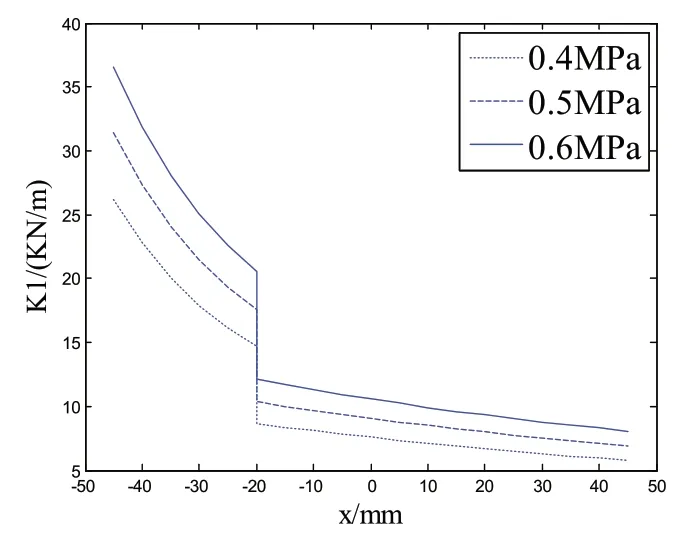
图3 前减振支柱总成刚度与行程的关系

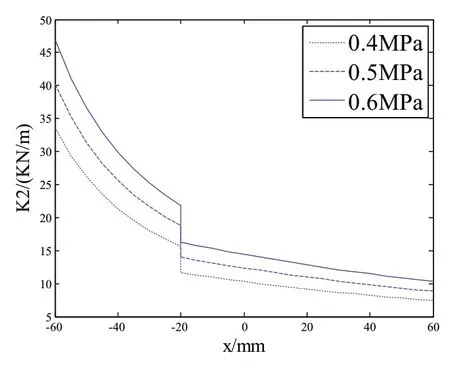
图4 后减振支柱总成刚度与行程的关系

3.2.2 总成弹性力的仿真分析

利用MATLAB/Simulink 仿真模型，将表2 相关性能参数代入，仿真模型的初始充气压力设定为0.4MPa、0.5MPa、0.6MPa 三种情况，对半主动悬架前、后新型一体式减振支柱总成弹性力与行程的关系进行分析，仿真结果如图5 和图6 所示。综合图5 和图6 均可以得出，当减振支柱总成处在相同的初始压力时，减振支柱的弹性力随着压缩行程的变大而变大，随着拉伸行程的变大而变小，并且呈非线性变化。还可以得到随着减振支柱总成主气室初始压力的变大，减振支柱的总成弹性力也随之变大。

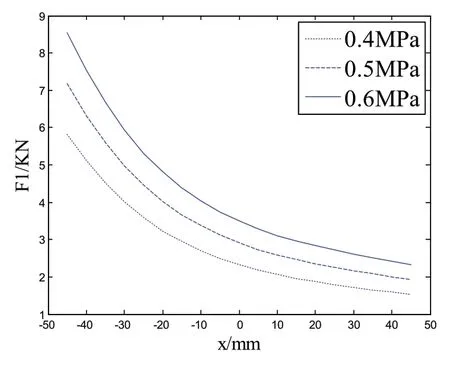
图5 前减振支柱总成弹性力与行程的关系

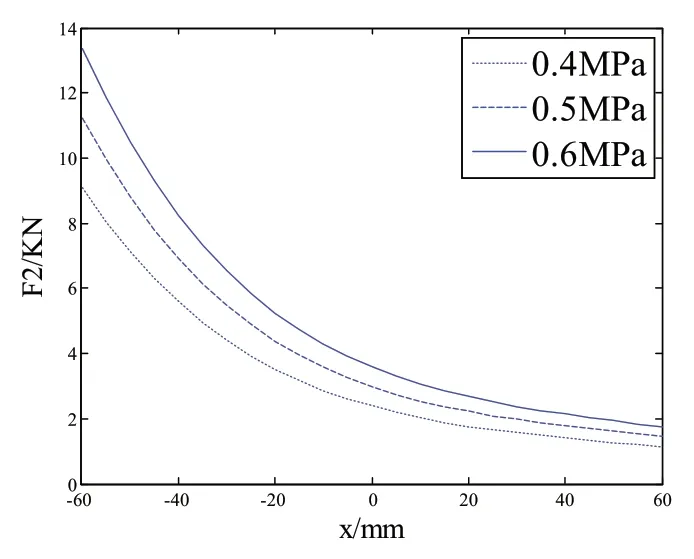
图6 后减振支柱总成弹性力与行程的关系

4 结语

为了提高汽车行驶平顺性和操纵稳定性，提出了一种半主动悬架减振支柱一体化结构，利用MATLAB/Simulink仿真工具，对新型一体式减振支柱刚度特性进行仿真分析，发现对悬架前后减振支柱与行程的关系进行的仿真图中，当行程为-20mm 时，前后减振支柱总刚度均呈现阶跃，满足半主动悬架减振支柱刚度的基本要求，为搭建半主动悬架一体化减振车辆整车性能分析提供理论。