基于威布尔分布的经济性与高可靠度智能电表维修周期预估算法

李维波 苏文斌 徐成虎 张茂杰 方华亮

基于威布尔分布的经济性与高可靠度智能电表维修周期预估算法

李维波1苏文斌1徐成虎1张茂杰1方华亮2

（1. 武汉理工大学自动化学院，武汉 430070； 2. 武汉大学电气与自动化学院，武汉 430072）

智能电表的可靠性寿命预估对设计的极端重要性，将为智能电表的维修工作带来显著便利。基于智能电表运行时间数据分析，建立二参数威布尔分布模型，确定二参数威布尔分布的参数。计算得到相应的分布函数和可靠度函数，确定在可靠度为90%时的预防性维修周期和最小维修费用对应的预防性维修周期。运行实践和实际算例表明，所提出的智能电表预防性维修周期预估方法，可以为优化批次电能表的检定及轮换周期提供决策依据，大幅度节省运维成本。

智能电表；二参数威布尔分布；可靠度；最小费用；预防性维修

0 引言

近年来，我国不断推进电力体制改革，增强和扩大智能电网建设规模，特别是“双碳”政策深入人心，我国在智能电网发展的背景下，在全国范围内推进并普及智能电表的使用，2022年国家电网智能电表招标数量将达7 736.35万只。随着科技的发展，智能电表在增加电子元器件使其更加智能、更加便捷的同时，也导致其结构更加复杂，引发的故障随之增加。可靠性是衡量智能电表质量的重要指标，直接影响智能电网的正常运行，甚至关系到用户的切身利益与社会的和谐稳定。同时，由于电表企业对智能电表可靠性预计的重要性认识不够，缺乏对智能电表的可靠性寿命方面的设计研究，致使目前电表的维修更换工作困难重重。因此，亟需一套可靠有效的智能电表可靠寿命及预防性维修预估方法，为批次电能表检定及轮换周期的优化提供决策依据，最大程度地减少不必要的预防性抽检及轮换，节省运维成本。

国内在电能表评价及寿命预测方面的研究已经取得很多成果。文献[1]采用Bootstrap方法处理现场数据，得到智能电表可靠性模型参数的离散分布，采用Bayes方法结合加速寿命试验数据得到融合两种信息后的参数估计值，实现智能电表的可靠性评估；文献[2]采用分层抽样的方法对智能电表进行抽样，综合考虑温度和湿度对误差的影响，建立威布尔分布模型，验证了寿命预测方法的可行性；文献[3]采用混合威布尔分布模型，选取三个故障率较高的因素对智能电表进行了可靠性分析；文献[4]采用随机森林模型对海量智能电表数据进行分析，建立了智能电表故障预测和寿命预测模型；文献[5]采用回归分析中的最小二乘法对威布尔分布和加速寿命试验模型的参数进行估计，并提出了参数改进的方法；文献[6]采用双指数参数分布模型，利用Peck加速模型，得到智能电表通信模块的可靠度函数，进而提出了通信模块可靠性提升措施；文献[7]采用一种自适应加权系数的威布尔分布，综合考虑温度和湿度的影响，来预测智能电表使用寿命；文献[8]分析了元件应力法、基于可信度试验的可信度预测法和基于可靠性试验的可靠性预测法的优缺点；文献[9]采用威布尔分布对谷物干燥机进行了可靠性分析；文献[10]对风机的故障模式进行分类，研究了以降低维修费用为目标来确定维修周期的方法。

大多数研究人员在选择模型时没有进行模型先验，影响了其分布模型的选择，导致其参数估计准确度不高，而且大多数研究是基于运行中电能表的信息，从可靠性的角度对电能表进行评估和寿命预测，而基于故障数据进行分析的研究很少，同时众多文献在阐释基于可靠性寿命评估时并没有考虑维修费用的影响。本文基于河南许继集团智能电能表故障数据，依据历史维修数据获得试验数据，利用威布尔分布图确定该组数据服从威布尔分布，对威布尔分布参数进行估计，并利用K-S检验确定参数的合理性；对智能电表进行故障概率密度分析和可靠性分析，在此基础上融入最小费用预防性维修周期预估分析，以适应于当前新型电力系统的发展 趋势。

1 基于K-S检验的威布尔分布算法

1.1 威布尔分布

威布尔分布在可靠性工程中得到广泛应用，尤其适用于机电类产品磨损累计失效的分布形式。大多数电子机械产品的寿命都符合威布尔分布，其形状参数能够整体描述出“浴盆”曲线的各个阶段。

目前，用于参数估计的常用分布方法包括指数分布、威布尔分布和正态分布。其中，威布尔分布可以利用大量实际运行故障数据，借助数理统计手段和可靠性理论，得到智能电表可靠度随运行时间变化的规律。

威布尔分布函数()的表达式为

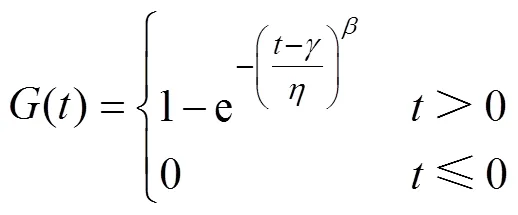
式中：为形状参数；为尺度参数；为位置参数；为时间参数。

威布尔分布包括二参数威布尔和三参数威布尔两种形式。当位置参数 ≠0时，威布尔分布为三参数威布尔分布；反之，当位置参数 =0时，威布尔分布为二参数威布尔分布[11-12]。

假设智能电表故障时间符合威布尔分布模型，模型随机变量为智能电表从开始运行到发生故障的时间，由于智能电表从开始投入运行到发生故障的时间是随机的，可能从刚投入使用就会发生故障，因此智能电表故障时间的威布尔分布模型的位置参数为0，即 =0。

对于二参数威布尔分布，其故障概率密度函数()可以表示为

故障概率分布函数()为

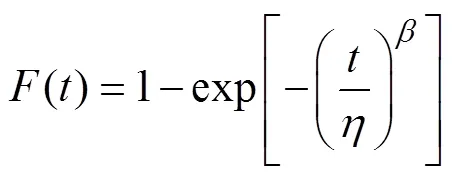
可靠度函数()为

形状参数影响威布尔分布函数曲线形状，根据值的不断变化，其故障概率密度曲线和可靠度曲线都会随之变化。尺度参数影响概率密度曲线的高度和宽度，若令=e-1可得()=，表示产品运行可靠度为36.8%时的工作年限，因此也被称为设备的特征寿命。

1.2 K-S检验

常用的检验样本分布类型的方法有2检验、K-S检验，其中K-S检验比2检验效率高，而且对小子样也很适用。相比2检验，智能电表故障时间数据在未知数据分布的情况下，选用K-S检验法是十分方便、有效的[13]。

K-S检验是一种基于经验分布函数的假设检验方法。K-S检验是将假设的理论故障概率分布()与样本观测值的累积分布0()进行比较，找出它们之间的最大差异，并参考采样分布来确定差异是否为偶然。

设样本容量为，将样本点从小到大依次排列，得到1,2,…,t，其经验分布函数F(t)为

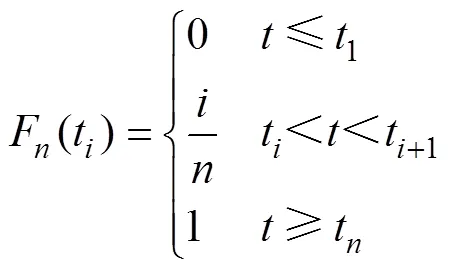
计算样本累积分布函数和理论概率分布函数之间的绝对差，使最大绝对差为D，其表达式为

如果满足式（6），则可以认为拟合令人满意，并且可以接受假设。

2 基于拟合优度检验的参数估计方法

2.1 数据处理

本文选择河南许继集团的4 763台智能电表运行数据进行分析。将每台智能电表运行时间从小到大进行排列，部分故障数据相关参数值见表1。

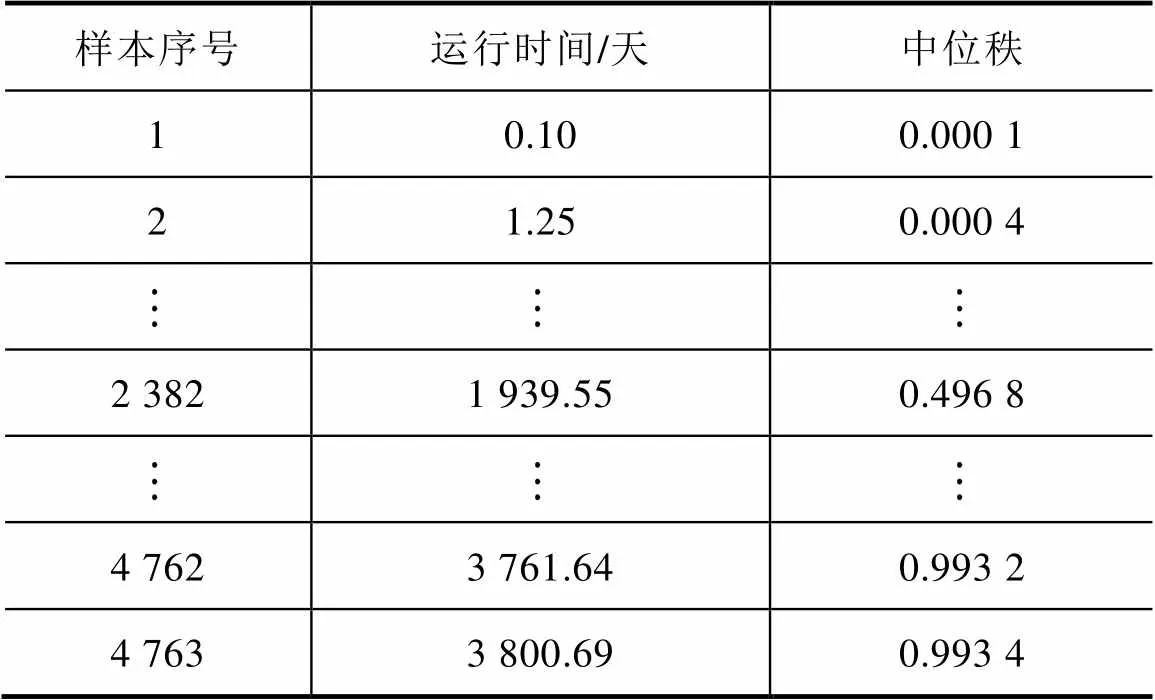
表1 智能电表故障数据的参数值

智能电表运行时间的威布尔拟合效果如图1所示。

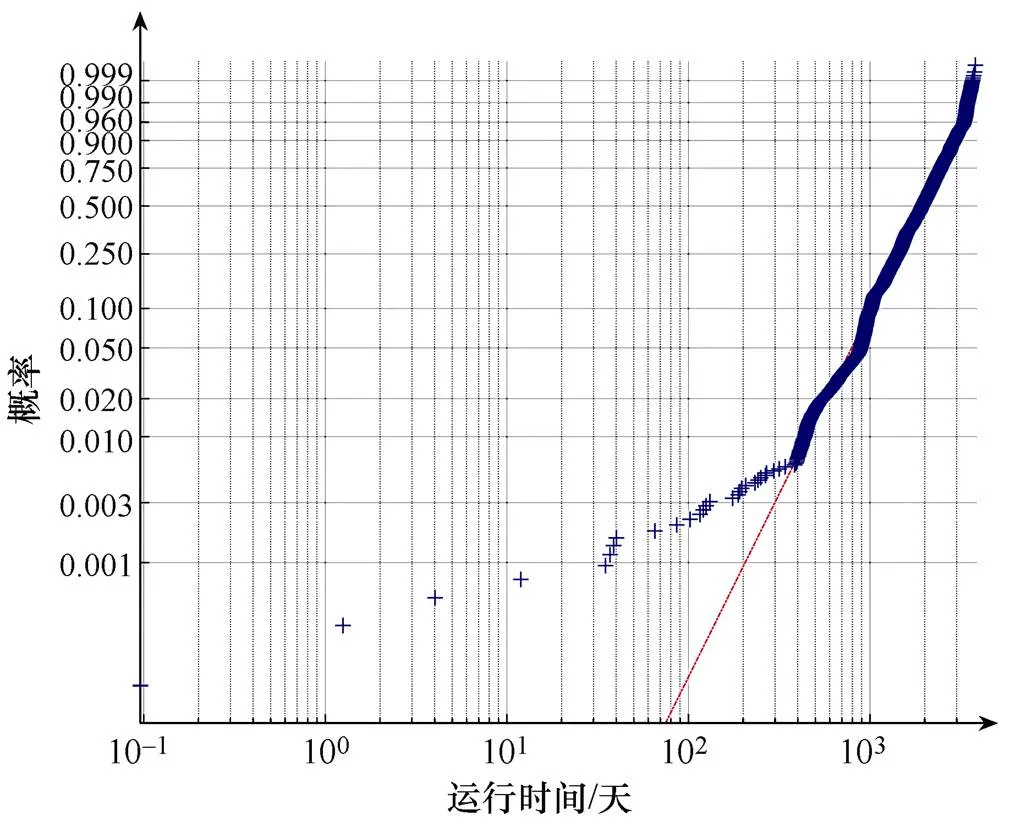
图1 智能电表运行时间威布尔拟合效果

分析图1可以看出：大部分数据近似呈一条直线分布，因此可近似认为该组数据服从威布尔分布。据此，选择最小二乘法对参数进行估计[14]。

2.2 参数估计

对于二参数威布尔分布的故障概率分布函数，等式两边进行变换后，可得

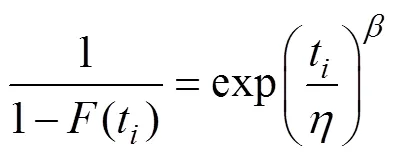
然后再对式（7）连续取两次对数，且经线性化处理，可得

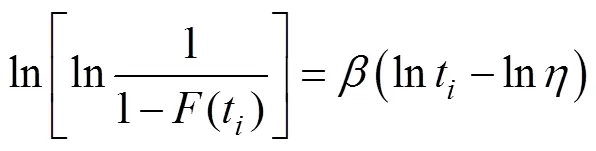
根据回归分析法则，可以推导得出参数、、和的估计值表达式分别为

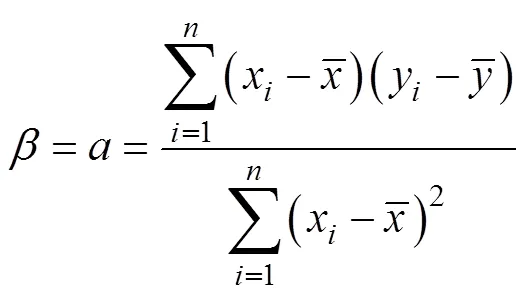
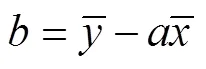
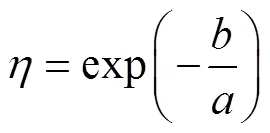
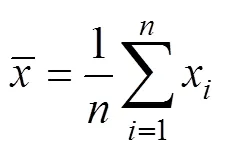
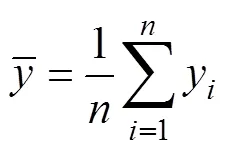
得到上述关系式后，采用近似中位秩公式（15）的计算值作为估计值[15]，即

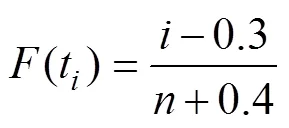
代入智能电表故障数据，可以计算出二参数威布尔分布的参数为 =2.433 0， =2 275.2。

2.3 拟合优度检验

根据计算出的二参数威布尔分布的参数值，可以得到累积分布函数0()的表达式为

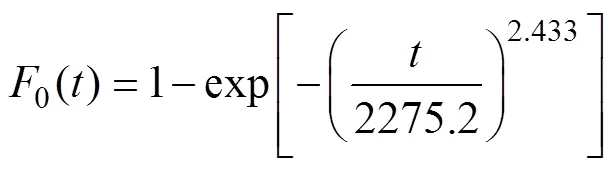
因此，统计量D可以表示为

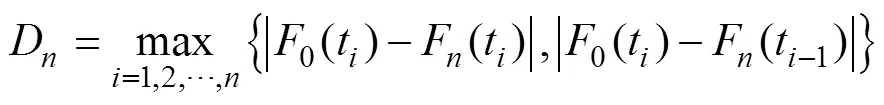
联立式（5）和式（17），将统计量D表示为

将智能电表运行时间数据代入式（18），可以得到拟合优度检验的相关结果见表2。

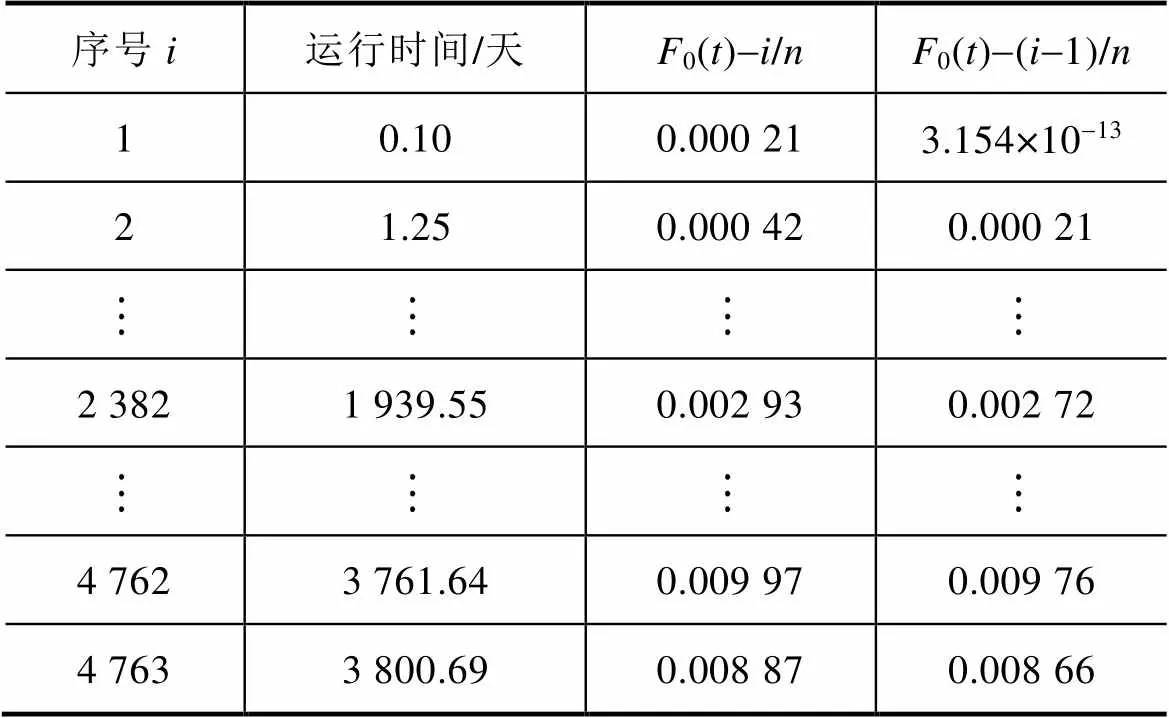
表2 拟合优度检验

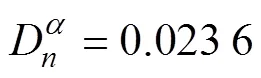
3 获取高可靠度的维修周期预估方法

3.1 故障概率密度函数

将二参数威布尔分布的形状参数和尺度参数代入式（2），得到智能电表运行时间的概率密度函数()为[15-16]

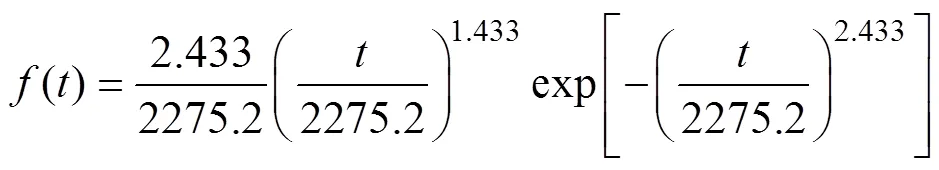
相应地，智能电表运行时间的概率密度函数f(t)曲线如图2所示。

分析图2可以看出，智能电表运行时间的概率密度函数的极大值点在1 580天左右出现，说明智能电表无故障工作时间的众数是1 580天，这意味着在正常工作1 580天以后，要进行一定程度的大检修，所以预防性维修周期为1 580天左右。

3.2 可靠度函数

将二参数威布尔分布的形状参数和尺度参数值代入式（4），则智能电表运行时间的可靠度函数()为

智能电表运行时间的可靠度函数()的曲线如图3所示。

分析图3可知，计算得出的威布尔分布拟合效果与源数据样本相差较小，拟合效果较好，能较好地预测出智能电表可靠性趋势[17-18]。随着智能电表运行时间变长，可靠度不断降低。为了保证智能电表的可靠性，取可靠度为0.9时，计算预防性维修周期。假设需要的可靠度为R，且在()≥R的条件下，智能电表的工作周期可以表示为

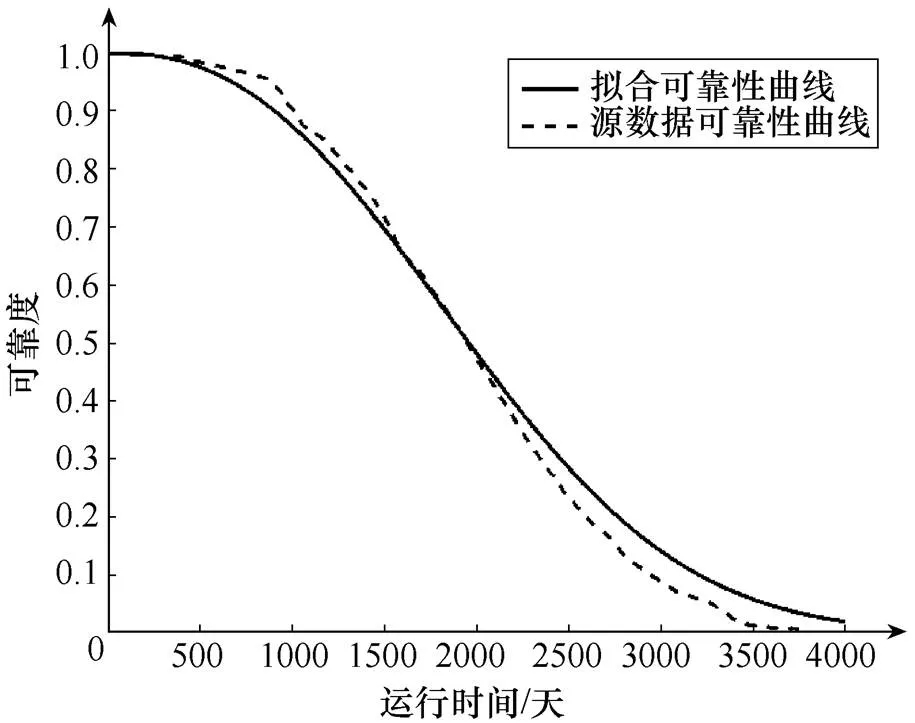
图3 智能电表运行时间的可靠度函数曲线

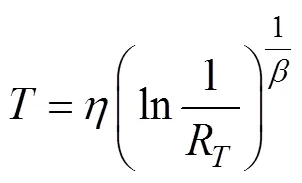
将二参数威布尔分布的形状参数和尺度参数代入式（21）可以看出，当可靠度越小时，智能电表的预防性维修周期越长。不同可靠度下智能电表预防性维修周期见表3。

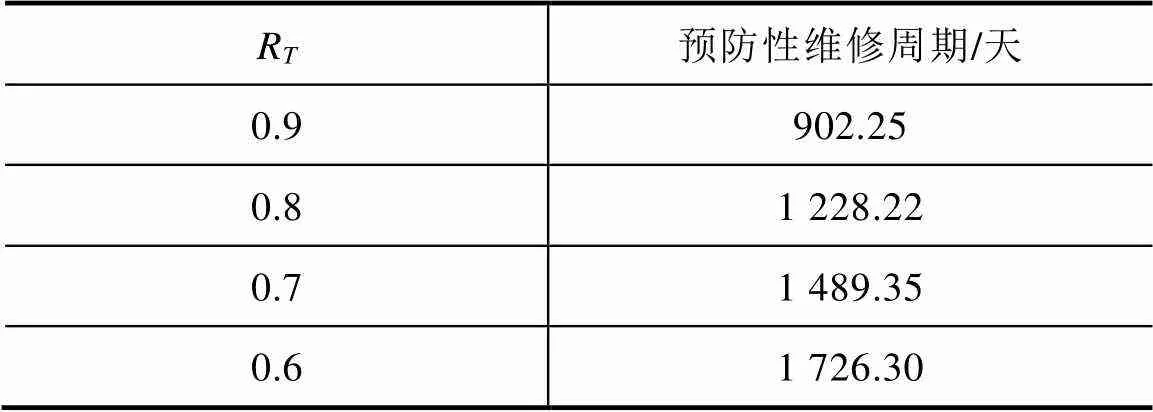
表3 不同可靠度下智能电表预防性维修周期

分析表3可以看出，可靠度为0.9时，智能电表预防性维修周期为902天。

智能电表平均寿命公式为

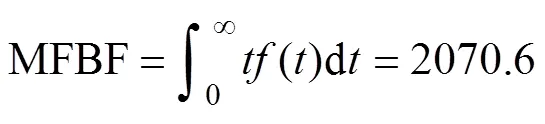
式（22）表明，智能电表的平均寿命为2 070天左右。

对照分析得知，由于智能电表按照可靠度为0.9计算出的预防性维修周期最小，因此，按照可靠性确定的检修时间为902天。

4 获取最低费用的维修周期预估方法

最佳维修周期不仅与设备的可靠性有关，还与设备的维修成本有关。在满足设备可靠性的前提下，要求设备的维护成本最低。为了使总维修费用最小，要考虑到预防性维修的费用与发生故障之后维修费用的比值关系，以经济效益最大来决定维修周期[19]。

假设为定期预防性维修周期，p为定期维修平均费用，f为智能电表发生故障后事后维修平均费用，一般有f＞p。智能电表的更换或维护时间与运行时间相比较短，可以忽略不计。在每个周期的平均工作时间MUT内，进行预防性维修费用的比例为可靠度函数()，进行故障维修费用的比例为不可靠度函数()=1-()。所以在单位时间内的维修费用为

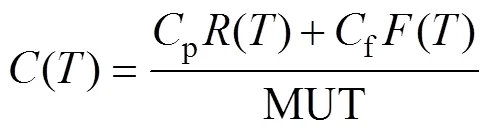
式中，MUT为设备在每一周期内的平均工作时间。

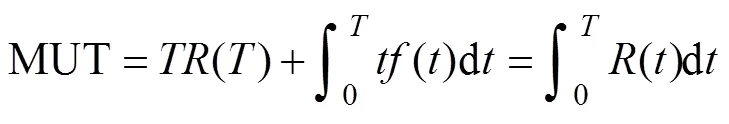
将式（24）代入式（23），得到单位时间维修费用()的表达式为

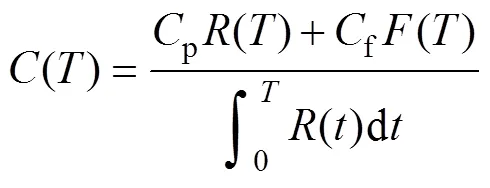
假设对智能电表进行定期维修的费用为Cp=40元，事后维修的费用为Cf =300元，代入式（25），得到智能电表单位时间维修费用C(T)随运行时间变化的曲线如图4所示。

分析图4可知，当智能电表运行时间为915天时，单位时间维修费用()取得最小值为0.075 39元。因此，在智能电表运行915天时，对智能电表进行预防性维修，所需的平均维修费用最小，一台智能电表运行一年所需的最小平均维修费用为27.52元。

综上所述，智能电表预防性维修周期的确定流程如图5所示。

图5 智能电表预防性维修周期的确定流程

根据智能电表运行数据，可以得到可靠度预防性维修周期和最小费用维修周期，而每个地区对可靠度和维修费用的侧重点也不相同，因此可以根据原始数据和实际运行要求，得到最符合标准的预防性维修时间。

在得到可靠度预防性维修周期和最低费用预防性维修周期后，如果在实际运行中对可靠度要求更高，则更应该关注可靠度预防性维修周期的情况，关注智能电表概率密度曲线和可靠度曲线，根据实际运行要求来选择预防性维修周期。如果在实际运行中对可靠度要求不是很高，而是更关注经济效益，那么在满足最低可靠度要求的前提下，应选择预防性维修周期费用最小的运行时间作为预防性维修周期。如果在实际运行中对可靠度有较高的要求，同时对维修费用也有较高要求，那么应该综合考虑可靠度和维修费用。如果按照可靠度要求得到的预防性维修周期比按照最低费用得到的预防性维修周期小，则按照可靠度要求来选择预防性维修周期；如果按照最低费用得到的预防性维修周期比按照可靠度要求得到的预防性维修周期小，则按照最低费用来选择预防性维修周期。

5 结论

为了提高智能电表的使用寿命，减小维护和更换的费用，运用可靠性理论和维修费用理论对河南许继集团某一批次智能电表的使用寿命和维修费用进行了分析研究，得到如下结论：

按照可靠性要求，智能电表预防性维修周期应在902天左右；在定期维修费用为40元、事后维修费用为300元时，按照经济性性要求，智能电表预防性维修周期应在915天左右，对应单位时间内最小维修费用为0.075 39元。

[1] 李若茜, 肖霞, 梅能, 等. 基于Bayes和Bootstrap方法的智能电表可靠性评估[J]. 南方电网技术, 2022, 16(3): 76-81.

[2] 滕永兴, 曹国瑞, 杨霖, 等. 基于混合威布尔分布的电能表寿命预测研究[J]. 电气传动, 2021, 51(1): 61-66.

[3] 肖勇, 胡珊珊, 许卓, 等. 智能电表通信模块可靠性评估[J]. 南方电网技术, 2020, 14(8): 52-57.

[4] 黄吉涛, 樊博, 周媛奉, 等. 基于随机森林的智能电表故障及寿命预测模型[J]. 兵工自动化, 2019, 38(10): 57-60.

[5] 杨国燕, 关靓. 基于回归分析的智能电表可靠性分析方法[J]. 黑龙江大学自然科学学报, 2019, 36(4): 498-504.

[6] 张蓬鹤, 张保亮, 陈思禹. 基于分层抽样的运行智能电能表剩余寿命预测方法研究[J]. 电测与仪表, 2019, 56(5): 148-152.

[7] FU Yihao, WANG Jun, XUE Shengjuan, et al. A new life prediction method of intelligent meters based on adaptive weighting coefficients[J]. Journal of Physics: Conference Series, 2020, 1654(1): 012085.

[8] YAO Haowei, WANG Xiaowei, WU Lusen, et al. Prediction method for smart meter life based on big data[J]. Procedia Engineering, 2018, 211: 1111-1114.

[9] 文昌俊, 陈哲, 徐云飞, 等. 基于威布尔分布的谷物干燥机可靠性分析[J]. 机电工程, 2022, 39(7): 972- 977.

[10] 李彪, 柴江涛, 吴仕明, 等. 基于最小期望维修损失的风电机组部件定期维修策略研究[J]. 河北电力技术, 2018, 37(2): 29-32.

[11] 周湶, 熊涛涛, 江天炎, 等. 连续方波脉冲电压下PCB绝缘可靠性的多变量威布尔失效模型[J]. 电工技术学报, 2019, 34(6): 1310-1318.

[12] 韦先灿, 高伟, 杨耿杰. 基于改进动态线损估计的智能电表误差估计方法[J]. 电气技术, 2022, 23(2): 7-12.

[13] 冯振宇, 诸德培. 威布尔分布的拟合优度检验[J]. 机械强度, 1996, 18(4): 28-31.

[14] YANG Fuli, HOU Xingzhe, PAN Guangze, et al. Research on reliability modeling and evaluation method of smart meter[C]//2018 IEEE International Conference on Automation, Electronics and Electrical Engineering, Shenyang, China, 2018: 244-248.

[15] 孙谊媊, 李宁, 董小顺, 等. 智能电表可靠性预计的优化模型[J]. 电力科学与技术学报, 2017, 32(3): 15-21.

[16] 王辉, 郝丽丽, 黄梅, 等. 基于历史故障信息的配电网设备故障概率建模[J]. 电力自动化设备, 2020, 40(3): 76-84.

[17] ZHOU Lixia, LI Wenwen, YUAN Ruiming, et al. Comprehensive evaluation of reliability life and economy of electric energy meter considering inter- mittent operation mode[C]//2021 IEEE China Inter- national Conference on Electricity Distribution (CICED), Shanghai, China, 2021: 238-243.

[18] 董宸, 夏彦辉, 孙丹. 基于全寿命周期理论的微电网优化配置[J]. 电气技术, 2020, 21(3): 59-63.

[19] 裴峻峰, 王丝雨, 任明晨, 等. 空冷器风机的可靠性研究[J]. 机械设计与制造, 2020(8): 215-219.

Maintenance cycle prediction method for smart electricity meters based on Weibull distribution with economy and high reliability

LI Weibo1SU Wenbin1XU Chenghu1ZHANG Maojie1FANG Hualiang2

(1. School of Automation, Wuhan University of Technology, Wuhan 430070; 2. School of Electrical Engineering and Automation, Wuhan University, Wuhan 430072)

The critical importance of reliability life estimation for the design of smart meters will bring significant convenience to the maintenance of smart meters. Based on the analysis of smart meter running time data, the two-parameter Weibull distribution model is established and the parameters of the two-parameter Weibull distribution are determined. The corresponding distribution function and reliability function are calculated to determine the preventive maintenance cycle when the reliability is 90% and the preventive maintenance cycle corresponding to the minimum maintenance cost. The operation practice and practical example shows the proposed preventive maintenance cycle prediction method for the smart electricity meters can provide decision-making basis for optimizing the verification and rotation cycle of batch electricity meters, which can greatly save operation and maintenance costs.

smart meter; two parameter Weibull distribution; degree of reliability; least cost; preventative maintenance

国家重点研发计划课题（2020YFB1506802）

国家自然科学基金面上项目（51977164）

2022-09-13

2022-11-11

李维波（1973—），男，重庆市人，博士，教授，主要从事电力电子技术在电力系统中应用方面的研究工作。